浅谈数形结合在解题中的应用

摘 要：数形结合思想是高中数学中常用的一种解题方法，将数学问题以图形化的方式呈现出来，不仅能够有效简化解题思路，还能拓宽学生的数学思维能力。本文简单阐述了数形结合思想的内涵，并通过实际案例详细介绍了数形结合思想的具体应用，旨在能够帮助高中生更好地学习数学这门课程。

关键词：数形结合;解题方法;应用思路

引言：在高中数学解题中应用数形结合思想，不仅有助于培养高中生的数学思维能力，还能拓宽他们的解题思路，提高其数学学习效率，对于促进他们的数学学习成绩水平提升而言有着十分颇为积极的意义。近年来，随着高考制度改革的不断深入推进，除了考查学生对数形结合思想基本应用思路的掌握以外，还强调学生的思维创新能力，这就对高中生运用数形结合思想的解题能力提出了更高的要求。因此，高中数学教师在平时的教学过程中应注重加强对学生数形结合解题能力的知道，引导他们从传统的数与形结合的解题思路中跳脱出来，探索更为灵活、多样化的解题思路，从而有效提升课堂教学的效率和质量水平。

一、数形结合内涵分析

数形结合思想是指根据数与形之间的关系，将两者进行互相转化以解决数学实际问题。将数形结合思想应用于高中数学解题中，即是将数与数之间的联系用图形表示出来，将代数问题转化为几何问题，从而达到简化解题思路，解决实际问题的目的。在高中数学解题中应用数形结合思想，能够让学生更为直观化和清晰化地了解问题本质，降低解题难度，不仅能够显著提高学生的解题效率，还能增强他们对数学的学习兴趣和学习信心，有助于促进其数学综合素养水平的提升。

二、数形结合思想方法的应用

（一）以数助形思想的应用

几何图形虽然在传达数学信息方面要更为形象化、直观化一些，但就其转化过程来看，显得略为复杂和繁琐一些，而以数助形则可以有效简化问题本身的表现形式，从而令解题过程变得更加方面。例如，解析法、代数法等都是以数解决问题的具体表现。在教学过程中，高中数学教师应灵活地运用相关解题技巧来培养高中生的发散性思维能力，以数助形，精确解题。

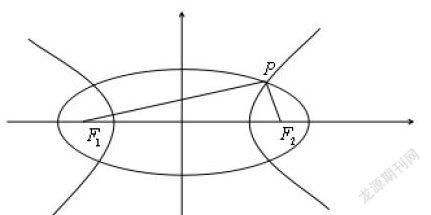
例1：已知有相同两焦点F1、F2的椭圆（m>1）和双曲线（n>0），点p是它们的一个交点，则的面积大小是（ ）

A. B. C.1 D.2

分析：结合上图，依题意得：

，将两式的平方相减得：

，即，所以S=1。

点评：熟悉圆锥曲线的定义十分重要，教师在平时的教学中应注重强调这方面的内容，让学生能够根据条件找到变量之间存在的某种恒定关系，透过外在表象思考其内在联系，从而在今后的解题中能够更加从容地应对各种题型。

（二）以形辅数思想的应用

以形辅数思想是指根据解题需要，从题目中已给出的数量关系反应到具体的空间图形上，从而找出隐藏的一些关键内容，以达到简化解题思路的目的。简言之，就是将原本抽象的数字关系以图形方式直观、形象地展现出来，构建相应的数学模型，从而简化解题步骤，如下面这道例题所示：

例2：已知（a、b为常数），若对于任意x∈R都有，则方程f（x）=0在区间[0，π]内的解为________________.

分析：根据题目中给出的“若对于任意x∈R都有”，可知，，三角函数图像取最低点，再结合函数解析式可知函数周期为π，因为三角函数的最值横坐标与相邻点之间相差四分之一个周期，即，所以在区间[0，π]内的解（即在区间[0，π]内的零点）为，即或

点评：这道例题看起来十分复杂，因为有字母a、b，然而，学生们在解题时只要理解了“三角函数的最值横坐标与相邻点之间相差四分之一个周期”这样的图像性质，再接三角形函数图像原理，问题便可迎刃而解。

從近几年来高考试卷中函数类型题目的出题规律来看，与图形之间的关系越来越为密切。高中生们在解题过程中如果脱离了图形思想，仅依靠想象力很难对问题进行全方位的把握和分析。数形结合思想的本质是根据数字与图形之间的联系，将原本抽象的数学语言用形象化的图形表现出来，或者用简洁的数学语言将复杂的图形表示出来，从而拓宽学生的解题思路，打开他们的数学思维空间，培养其灵活运用多种手段解决数学实际问题的能力，这对高中生今后的学习有很大的帮助。

三、结语

综上所述，随着高中课程改革制度的不断深入发展，高中数学教师也应及时更新自身的教学理念，将数形结合思想作为一种重要的解题思路传授给学生，引导他们学会将抽象的问题具体化，以切实提高他们的数学解题能力，促进高中生数学综合素养的提升，从而达到提高高中数学教学质量水平的目的。

参考文献

[1]葛玉锋.数形结合在高中数学解题中的应用[J].高中数学教与学.2018（07）

[2]黄朝斌.高中数学“数形结合”在解题中的应用[J].科学咨询（教育科研）.2018（05）

作者简介：朱磊，男，1982，01，30，籍贯：甘肃兰州，工作单位：乌鲁木齐十九中学，邮编，830000，研究方向：中学数学教育学历：大学本科，职称：中教一级教师