小学数学课堂提问“五要素”

徐惠

摘要：课堂提问是一门精致的艺术。小学数学课堂的提问应适当设计一些多思维指向、多思维途径、多思维结果的问题，培养学生的思维能力;找准“已知区”与“最近发展区”的结合点，即知识的“增长点”，让学生“跳一跳，够得到”;引发认知冲突，激起学生的学习动机和兴趣;设计环环相扣的问题，帮助学生由易到难地进行探究，突破学习难点;做出恰当的反馈，帮助学生凝练观点，总结提升。

关键词：小学数学课堂提问思维反馈

课堂提问是一门精致的艺术，承担着培育学生思维的使命，联结着学生的“最近发展区”，能够引发学生的认知冲突，帮助学生突破学习难点，凝练观点，总结提升。笔者以为，小学数学课堂提问应重点关注以下五个要素：

一、聚焦思维

现代教学论认为：学生有了问题，才会有思考和探索;有了思考和探索，才会有创新，才会有发展。问题的提出是促使学生形成良好认知结构的推动力，也是培育学生思维的重要手段。小学数学课堂应适当设计一些多思维指向、多思维途径、多思维结果的问题，培养学生的思维能力。

例如，教学“百分数的意义”后，教师提问：“什么是百分数？是不是分母是100的分数就一定是百分数？”在引导学生对百分数和分数进行区分后，教师在应用百分数环节又设计这样一个问题：“选数：200%、45%、100%、86.9%、101%、95100。九月份实际生产的零件数是计划的（），括号里可以填什么？表示什么？”学生通过思考可以发现：若括号里填的数大于100%，则说明实际生产的零件数多于计划生产的零件数;若括号里填100%，则说明实际生产的零件数和计划生产的零件数一样;若括号里填的数小于100%，则说明实际生产的零件数比计划生产的零件数少。同时，这里也可以填分数95100，表示两个数量比较的结果。

开放性的问题使学生进一步理解了百分数和分数的意义，培养了思维的发散性。

二、着力发展

心理学认为，人的认知水平可划分为三个层次：“已知区”“最近发展区”和“未知区”。学生认知水平的发展就在这三个层次之间循环往复，不断转化，螺旋上升。小学数学课堂的提问应找准“已知区”与“最近发展区”的结合点，即知识的“增长点”，让学生“跳一跳，够得到”。

例如，《长方形和正方形》一课的教学片段——

师（取出一个信封）老师手里是一个信封，里面装了一些四边形，请根据提示来猜一猜它是什么图形。（提示）这个四边形对边相等。

生正方形。

生长方形。

师哦，要么猜正方形，要么猜长方形，你们猜得对不对呢？（抽出部分，如图1）瞧，这个四边形偷偷地露出了一个角。

图1

生（七嘴八舌）既不是正方形，也不是长方形。

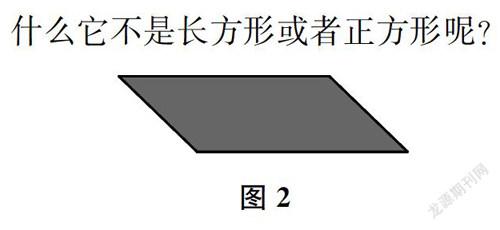
师怎么改主意了？（抽出全部图形，如图2）咦，这个图形明明就是对边相等的呀，为什么它不是长方形或者正方形呢？

图2

生因为它的角不是直角。

师哦，看一个图形是不是长方形（正方形），既要看它的——

生边。

师还要看它的——

生角。

三、引发冲突

采用精巧的角度进行课堂提问，能够创造积极的课堂气氛，激发学生的学习动机和兴趣。引发认知冲突就是其中一种方法。

例如，《认识厘米》一课的教学片段——

师男生测量的线段有5根小棒这么长，女生测量的线段有4根小棒这么长。那谁测量的线段长一点呢？

生男生。

师确定吗？（出示图3）我们一起来比比看。

图3

生女生的长。

师咦，刚才你们不是异口同声很坚定地说男生的长吗？看来要比较线段的长短，用的小棒长度要——

生一样长。

师对，一样长。所以，我们规定了单位长度，就是我们今天要学习的厘米。

四、突破难点

当遇到难度较大的问题时，教师应当降低学生思考的难度，可以围绕总问题设计若干子问题，引导学生由易到难，由简到繁，由浅到深，层层递进地开展探究活动。

例如，《认识10以内的数》一课教学。教师教学了数字1-5后，让学生按照从小到大的顺序排一排，然后提问：看一看，想一想，数字2在谁的后面？在谁的前面？这个问题比较简单直观，许多学生马上得出了结论。紧接着，教师抛出问题：我们能不能把这两句话合并成一句话呢？想一想，数字2在谁和谁的中间？这个问题建立在学生观察并理解大小顺序的基础上，强化了2的取值范围。接下来，教师遮住了数字的顺序图，提问：3和5的中间是谁？

环环相扣的三个问题，由易到难，帮助学生对数序进行了概括，突破了学习难点。

五、总结提升

在提问之后，教师对回答的反馈（点评）也很重要。教师的提问与反馈不应面面俱到，而要加深学生对知识本质的理解和對知识内涵的挖掘。精当的反馈可以引导学生纵横联想所学知识，凝练观点，总结提升。

例如，《认识负数》一课教学。教师出示图片，上面标有A、B、C三个位置，说明：A是珠穆朗玛峰，海拔8844米;B是黄山，海拔1873米;C是海平面。在学生观察后，教师提问：如果把A的高度记作0，那么B的高度该怎么表示？学生思考后发现，此时B处于基准线以下，应该用负数来表示。接着，教师又提问：为什么刚刚黄山的海拔是正数，现在却用负数表示呢？学生回答：因为现在把珠穆朗玛峰的高度看作0，那么所有比珠穆朗玛峰低的地方都用负数表示。教师及时进行总结反馈：对呀，看来一座山的高度究竟是正数还是负数并不是绝对的，它取决于我们取的基准值。

通过这样的提问和反馈，学生明白了：正数和负数并不是完全绝对的，而应该与基准值做比较;负数与正数并不是绝对的概念，而是一组相反意义的量。由此，学生深度理解了负数的意义与价值。