数学“慢化教学”的策略研究

摘要：教学过程中可能布满了沟沟坎坎，因此，它应该是润泽的、蹒跚的。这透射出的就是悠然之“慢”。“慢化教学”是关注知识深度理解、关注学生发展性的教学，追求的是“慢之有道，学之有效”。在数学知识教学中，慢化的策略有：激发认知需要，慢于自然;降低认知起点，慢中求真;拉长认知过程，慢中求实;拓宽认知渠道，慢中求透;挑起认知交锋，慢中求活。在数学习题教学中，慢化的策略有：一题作基演变，慢中明道;开放问题思路，慢中优术。

关键词：数学慢化教学知识教学习题教学

杜威说过：“教学绝不仅仅是简单的告诉，而应该是一种过程的经历，一种体验，一种感悟。”教学过程中可能布满了沟沟坎坎，因此，它应该是润泽的、蹒跚的。这透射出的就是悠然之“慢”。

笔者提出的全息观下的教学，有一种快慢相谐的基调。其中，“快”主要指整体统摄下的整体建构。但是，“快”必须有“慢”来助阵。“慢”是一种外在状态，它不是为慢而慢，更不是消极怠工，而是为了生成“快”的效果而采取“缓存”策略，是为了快步推进而蓄能蓄势，是基于学生学会、提升学力的“慢”。

布鲁纳说过：“学习不但应该把我们带往某处，而且应该让我们日后在继续前进时更为容易。”“慢化教学”就是基于此的教学，就是关注知识深度理解、关注学生发展性的教学，追求的是“慢之有道，学之有效”。笔者通过研究，在“慢节奏、慢引领、慢呈现、慢操作、慢思维、慢生成”的基础上，初步形成了“慢化教学”的一些策略。

一、知识教学

在知识教学中，理解是应用的基础，没有深入的理解，就不能灵活地应用。因此，知识的教学尤其要放慢节奏，促进理解，不能蜻蜓点水地滑过。

（一）激发认知需要，慢于自然

概念是命题的基础，理解命题首先要理解好概念。在概念教学中，放缓认知节奏首先要让概念的出现源于需要，揭示概念引入的必要性。这样，才真正有利于明晰概念的来龙去脉、前世今生，把握概念的内涵、外延，建构概念的结构体系，达到对概念本质的深度理解。

例如，方差概念的教学，可以让学生通过案例计算，发现平均数、中位数、众数这“三个代表”都不足以解决问题，由此使方差的出现成为学习的需要，合情入理。具体如下：

问题1供选项：A.平均数;B.中位数;C.众数。

（1）为了反映初二学生的平均年龄，应关注学生年龄的。

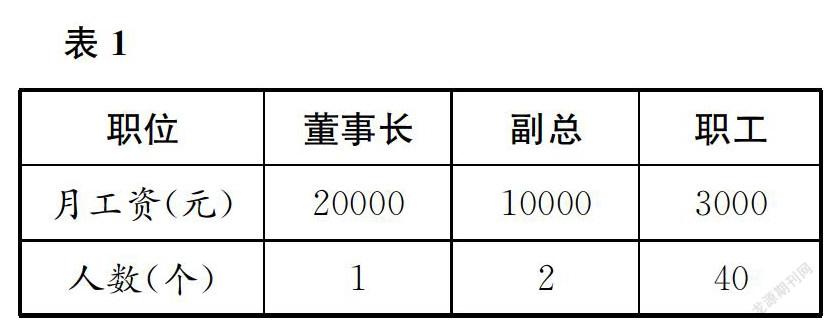
（2）表1是某公司的月工资报表。

为了了解这家公司人员工资的一般水平，应关注。

（3）为了考察某同学在一次测验中数学成绩是上游还是下游水平，应关注这次数学成绩的。

教学说明：以上是数据的“三个代表”，体现了数据的集中趋势。

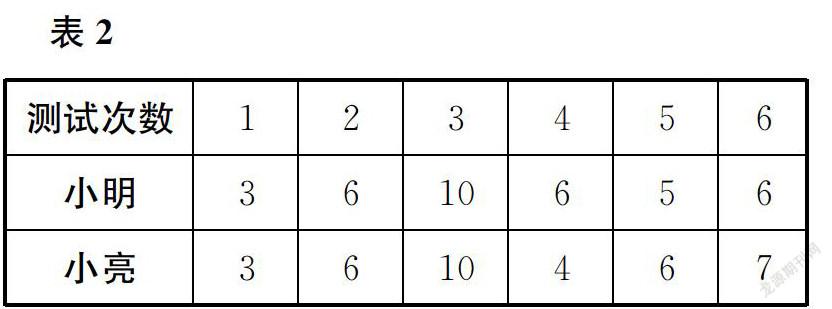
问题2小明和小亮是校射箭队的运动员，两人参加射箭测试，近期的6次成绩如表2所示（单位：环）。

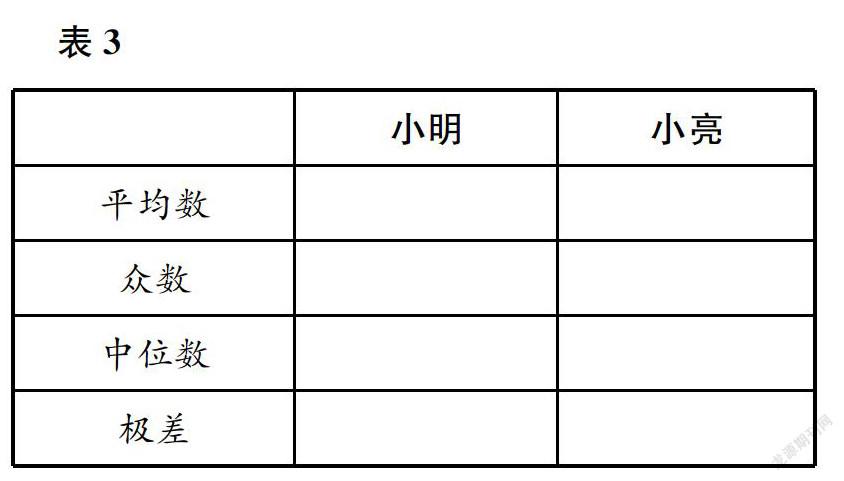
（1）根据表2填写表3。

（2）根据以上数据，你能选出参赛的队员吗？为什么？若不能，怎么办？

教学说明：通过计算，发现4组数据均相等，此时遭遇困境，怎么办？波折起伏，激荡起学生的探索欲望，接下来的新知学习就会成为学生的内需，其必要性、合理性得以彰显，新概念的现身就顺势而为了。

（二）降低认知起点，慢中求真

“低起高落”是数学的应有之态。低下去的目的是高起来。放低教学入口，降低认知起点，有利于激发学生学习的积极性，增进学生的参与热情，能让学生循阶而上，步步登高，厚积而薄发。

例如，配方法是数学中的重要方法。对于解一元二次方程而言，其重要性更是不可小觑，因为它是联结直接开平方法与求根公式法的纽带。基于此，在配方法的教学中，笔者设计递进问题，引导学生拾级而上，缓推慢行，品悟真味，求得真果。

问题1解方程x2=4。

问题2解方程x2+4x=0。

问题3解方程3x2+12x=0。

问题4解方程3x2+12x-4=0。

问题5解方程ax2+bx+c=0（a≠0，a、b、c为常数）。

从最简单的直接开平方的方程“低起”，到最一般的字母系数方程“高落”，其间可以体验配方法的形成过程，并获得求根公式的“副产品”，一举两得。

（三）拉长认知过程，慢中求实

一些重点知识需要实实在在地沉淀于学生头脑中，否则，容易淡忘，难以成为后续学习的“基地”，难以产生正迁移。对这样的重点知识，一开始学习时，就需要通过增设教学环节，拉长认知过程，在慢节奏中，将其做实。

例如，直线是几何学中的原始概念，是不定义的、超经验的，可谓几何教学的“第一粒紐扣”。由于直线概念看起来很简单，而且学生已有了一定的认知，很多教师往往高估了学生的原有认知，淡化直线概念的教学，导致学生认知模糊、理解不到位。对此，笔者精心设计了直线概念的教学环节：

环节1：说印象——突出直、线性、两端延伸的外形。

环节2：找实例——从生活中寻找实例，与现实生活对接，具象化直线。

环节3：画——一点画、两点画，感知存在性。

环节4：说感悟——立足“画”找感觉，赋予直线生命的灵性。

环节5：说应用——栽树、钉木条等，体会、感知“两点确定一条直线”。

环节6：表示直线——两种方法，立足现实应用，用两点（两点表示法自然生成两个大写字母），用小写字母。

环节7：意境化——用陈子昂的“前不见古人，后不见来者，念天地之悠悠，独怆然而涕下”，以时间的无始无终刻画直线，让直线这一图形充满诗情画意。

通过增设这些教学环节，从意象、物象、形象、抽象全方位地刻画直线概念，让这个不定义的原始概念在学生的头脑中扎下根来。

（四）拓宽认知渠道，慢中求透

“横看成岭侧成峰，远近高低各不同。”从多个角度观察、认识事物，往往看得真切、全面。数学教学也是同样的道理：多渠道、广视角地理解，看似缓慢，实则通透了核心知识，深化了理性认识，沉淀于脑，铭记于心。

例如，二次根式的反身性“（a）2=a（a≥0）”的教学，可从以下角度立体展开：

渠道1：利用互逆关系还原，可类比学生熟知的加减、乘除等互逆运算。

渠道2：借力完全平方数的计算，使抽象变具象，通过验证加强直感性，如（9）2=（32）2=32=9。

渠道3：数形结合，借助图形，利用正方形边长与面积的关系具象说明。

渠道4：回归算术平方根的概念，提升理性认识。

每一位学生的认知基础不同、思维方式不一，对同一个事物的理解也会不尽相同。多渠道的印证，既满足了不同学生的不同需求（合其势），又契合了学生的求异心理（循其道）;除了增强认同感，便于理解记忆外，还历练了学生的多向思维。

（五）挑起认知交锋，慢中求活

学习中，有些问题容易受常识的偏颇影响而滑过，成为“夹生饭”而不自知。实际上，就是一个简单的概念，也要有个子午卯酉的说法。通过开放问题的设计，激起思维碰撞，挑起认知交锋，可以让概念、公式、法则等“瓜熟蒂落”，获得丰富、灵活的表征。

例如，平方差公式的教学，为了揭示公式的结构特征，笔者抛出如下开放而又有一定挑战性的填空题：（○）（○）=a2-b2，除了填（a+b）（a-b）以外，还可以填什么？看谁填得多。此题激发了学生的探索热情，学生踊跃登台，写出如下一些式子：①（b+a）（a-b）;②（a+b）（-b+a）;③（a+b）（-a-b）;④（-a+b）（a-b）;⑤（-a+b）（-a-b）;⑥（-a-b）（-a-b）;⑦（a-b）（a-b）;⑧（-a-b）（a-b）……这些式子有的是对的，有的是错的。因此，学生开始讨论、肯定、批判。笔者抓住时机，发动学生找出所有正确的结果，然后提出问题：这些正确的式子有什么共同的特征？由于以上挑选出的式子基本穷尽了所有的变形形式，因此平方差公式的特征得到有效的揭示。

如此的慢化处理，突出了重点，化解了难点;充分暴露了学生的思维轨迹、认知弱点，让平方差公式的知识表征得以激活，结构特征得以凸显。

二、习题教学

习题的教学也要放慢节奏，提升价值，不能满足于就题解题。

（一）一题作基演变，慢中明道

有的题目内涵丰富，具有母题的价值，承载着数学知识内在的规律性。若以此为基，从中挖掘出生长点，使得题目不断演变，在变化的“术”中探寻出不变的“道”，可以帮助学生把握题目本质。例如：

习题1（人教版初中数学教材习题14.2“拓广探索”第7题）已知a+b=5，ab=3，求a2+b2的值。

以此题为基础，可编拟出题组展开教学，从变式中揭示规律，寻法问道：

（1）若a+b=5，ab=3，求a2+b2、a-b的值。

（2）若a2+b2=19，a+b=5，求ab、a-b的值。

（3）若a2+b2=19，ab=3，求a+b、a-b的值。

（4）若a+b=3，a-b=5，求ab、a2+b2的值。

（5）若ab=3，a-b=5，求a+b、a2+b2的值。

（6）若a2+b2=19，a-b=5，求a+b、ab的值。

通过这一组题目，帮助学生提炼出这一类问题的一般思路（基本量意识）：两数和、两数差、两数积、两数的平方和这四个量，给出任意两个量都能求出其他的量。有了这样“道”的认识，编拟问题就不在话下。

学生独立解答完成。若不顺利，就让学生通过小组交流化解问题;若顺利，则让学生尝试编题，从中加深对这一规律的认识。

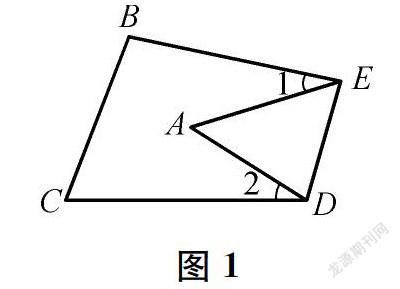
习题2如图1，把△ABC沿DE折叠，当点A落在四边形BCDE内部时，∠A与∠1+∠2之间有一种数量关系始终保持不变。请试着找一找这个规律，你发现的规律是（）

A. ∠A=∠1+∠2

B. 2∠A=∠1+∠2

C. 3∠A=2∠1+∠2

D. 3∠A=2（∠1+∠2）

解答：∠A=180°-（∠B+∠C）=180°-（∠AED+∠ADE），所以∠B+∠C=∠AED+∠ADE=180°-∠A，所以∠1+∠2=360°-（∠B+∠C+∠AED+∠ADE）=360°-2（180°-∠A）=2∠A。选B。

这是一道具有典型意义的题目，有可以深度挖掘的空间，是孕育问题意识和创新精神的优质素材。教学中，笔者让学生由此题编拟新问题，但是学生感到困难，于是笔者进行了引导：

师原问题中折叠后点A在四边形內部，同学们还可以提出怎样的问题？

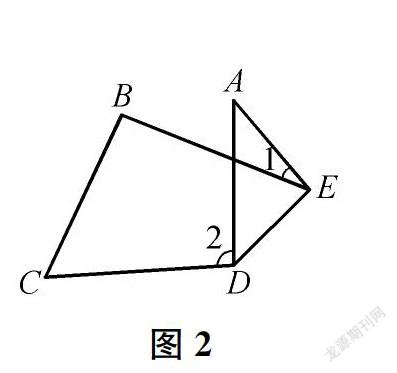
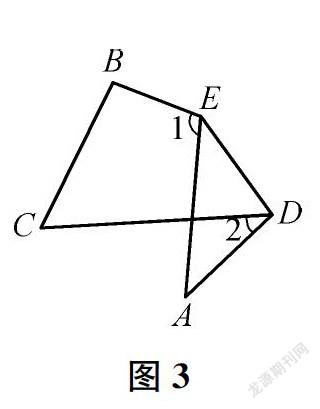
生（出示图2、图3）折叠后点A在四边形外部时，如图，∠A与∠1、∠2之间的数量关系是什么？

师你能猜一猜此时的结论吗？

生2∠A=∠2-∠1。

师原问题中折叠了一个角，我们还可以提出怎样的问题？

生折叠两个角、三个角。

师这是一个三角形问题，我们还可以编拟怎样的问题？

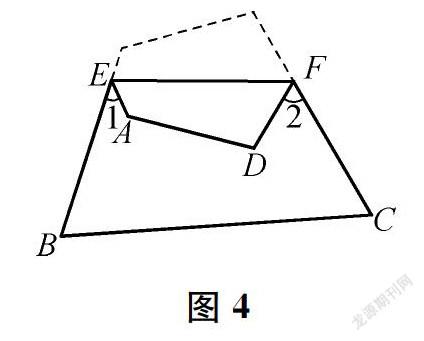
生（出示图4）四边形、五边形等问题，如图。

……

师梳理一下构建问题的策略：折叠在图形内部→折叠在图形外部（上、下或左、右）→折叠多个角→折叠其他多边形。这种策略是复合的，起初源于位置的不同提出问题，而后从数量的不同提出问题，最后从维度的不同提出问题。以上编拟问题的方法就是“what if not”法的扩展使用：不是这一个，还会是哪一个呢？问题滚滚而来。

这里，通过搭建支架，引导学生不断提出问题，让学生逐渐感悟问题提出的不同维度;通过梳理总结，帮助学生积淀刚刚获得的提出问题的初步经验，使之成为能发生迁移的比较成熟的经验，从而发展学生的问题意识，扩大学生提出问题的思维视域。

（二）开放问题思路，慢中优术

有的问题内涵丰富，可能蕴含多种解法。教学中，开放问题的思路，让学生尝试一题多解，有利于培养学生的发散性思维，让学生串联知识的内涵和外延，融会贯通;有利于培养学生的聚合性思维，让学生提炼方法的区别和联系，优化思维;还能让不同层次的学生找到学习的成就感，调动课堂的氛围。例如：

习题3在四边形ABCD中，∠ACB=∠BAD=105°，∠B=∠D=45°，求证：AB=CD。

对于此题，在教学中，可以引导学生秉持“有就找出来，没有造出来”的模型意识，发现需要构造辅助线解题，然后执果索因，追溯获得线段相等的基本方法之源头（三角形全等的性质或“等角对等边”），捕捉有用的信息，广泛搜索，形成如下思路：

解法1：如图5，过点C作CE∥AB，交AD于点E，即可构造出与△ABC全等的△CDE，进而得证。

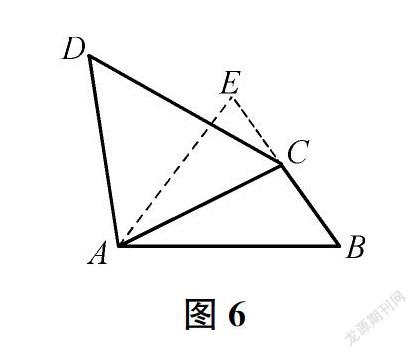
解法2：如图6，以AB为边作∠BAE=∠DCA=60°，AE交BC的延长线于点E，即可构造出与△ACD全等的△EAB，进而得证。

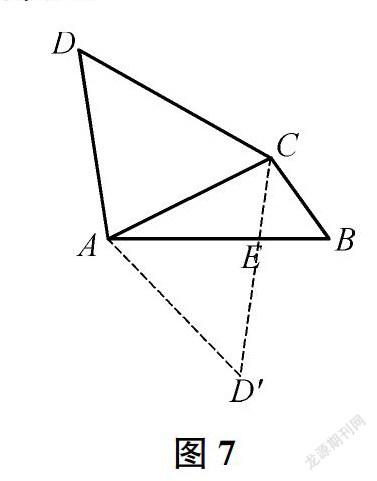
解法3：如图7，作点D关于AC的对称点D′，连结AD′、CD′，可证△AED′与△BEC均为等腰直角三角形，即得AB=CD′，进而得证。

解法4：如图8，同解法3，作点B关于AC的对称点B′，连结AB′、CB′，可证△CEB′与△DEA均为等腰直角三角形，即得AB′=CD，进而得证。

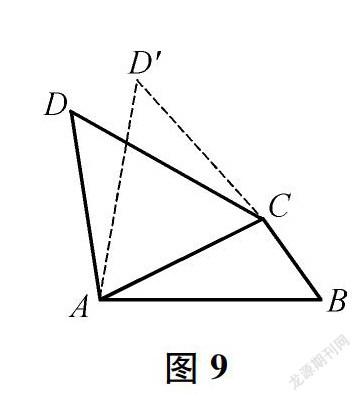
解法5：如图9，作∠ACD′=∠CAD，使CD′=AD，可得△DCA≌△D′AC，即有CD=AD′，然后可证B、C、D′共线，由∠B=∠D′=45°，得AB=AD′，进而得证。

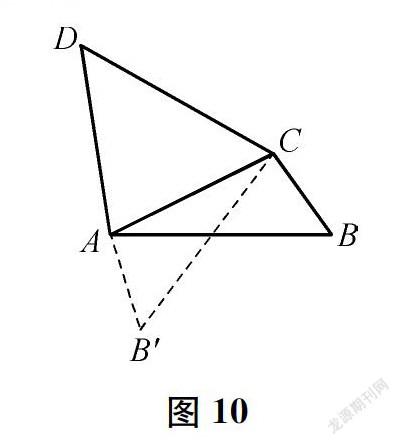
解法6：如图10，作∠CAB′=∠ACB，使AB′=CB，证法同解法5。

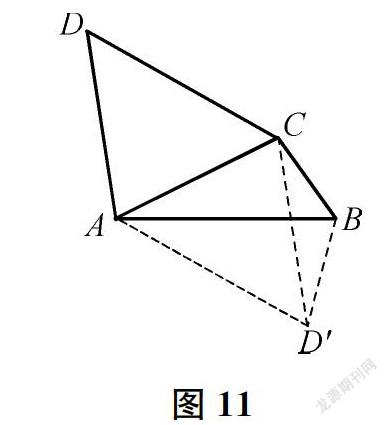
解法7：如图11，分别过点C、A作CD′∥AD、AD′∥CD，使两线交于点D′，连结BD′，可知四边形ADCD′是平行四边形，即有AD′=CD，然后可证∠ABD′=∠AD′B=75°，得AB= AD′，进而得证。

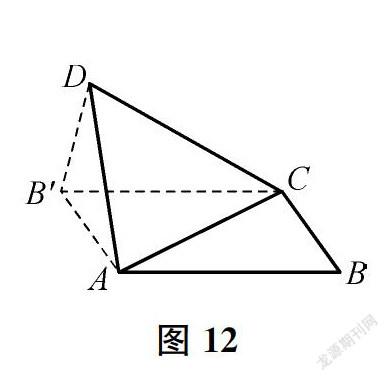
解法8：如图12，分别过点C、A作CB′∥AB、AB′∥CB，使两线交于点B′，连结DB′，证法同解法7。

统而观之，以上8种解法都落脚于构造全等三角形，且借力于“等角对等边”。另外，除解法1、解法2外，其他6种解法均是基于对称而有的思路，每一类思路的方法都是“成对”的。这契合了G.波利亚的“蘑菇”理论：当你发现一只蘑菇的时候，应当在边上再找一找，因为蘑菇总是成堆生长的。“再找一找”就是迁移，就是由此及彼、举一反三。

然后，引导学生在发散中凝聚，在多种解法中提炼共性，或通过讨论找出简洁的方法，进而达到优化思维的目的。如此的“慢化”才便于发挥题目的“内能”。

参考文献：

[1] 李相朋，马俊，俞光明.全息教学论初步探讨[J].武汉纺织工学院学报，1997（2）.

[2] 邢成云，王文清.整体建构，跨步推进——全息教学论下的整体教学尝试[J].中学数学杂志，2013（12）.

[3] 邢成云.追寻“快慢相宜”的整体化教学[J].江苏教育，2015（5）.

[4] 朱桂凤，孙朝仁.初中数学慢化教育的可行性调查与分析[J].中学数学杂志，2014（6）.

[5] 汪宗興，徐维武.小题大做，精彩绽放[J].中学数学教学参考（中旬），2015（Z2）.