小学数学“寻根式”试卷讲评策略

周艳

摘要：试卷讲评，如果选择“以题论题，题海再战”的模式，那么不仅会造成学生对所学知识无法达到深层理解、学以致用，也会压抑学生学习的主动性和积极性。试卷讲评，可以在数学认知里、思维生长处、学习履历中“寻根”，帮助学生找到知识、能力、兴趣等各方面素养成长的钥匙，打开数学世界和现实生活的一道道大门。

关键词：试卷讲评数学认知思维生长学习履历

随着素质教育的深化，小学数学总目标由“双基”扩展为“四基”，从“两能”发展为“四能”，数学教学更加指向促进眼下的数学理解与长远的素养发展。在这种课程背景下，教师如果还是选择“以题论题，题海再战”的试卷讲评模式，那么不仅会造成学生对所学知识无法达到深层理解、学以致用，也会压抑学生学习的主动性和积极性。不在“根”上破题，教师再用力，也可能是舍本求末的徒劳。

一、在数学认知里“寻根”

数学认知就是不断构建数学认知结构的心理活动，它是形成数学素养的基础。数学概念、数学规律（命题）、数学关系（理论）是数学认知的三个维度，同时也是试题命制的基础。因此，教师首先要分析试卷的内容、结构，明晰考查的数学概念、数学规律、数学关系是什么;然后分析学生的错误原因，发现学生数学认知上的缺陷，在讲评时有的放矢地解决这些缺陷和问题。

例如，以下是常见的学生进行列式计算产生的错误：

（1）125×32=（125×8）×（125×4）;

（2）120÷34—35=20×34—20×35;

（3）20×34+65×10=20×34+65×10。

这些错误，从题目类型、解法模式等方面加以分析，可以发现学生在“数与式”“乘法分配律与结合律”的认知上存在缺陷，因此在解题过程中容易受到干扰，从而造成错误。讲评时，不应只是简单地告知学生“应该这么做”，还应在知识的对比或联系处设计练习，直击知识中的易混点、易错点、内联点和区分点，暴露并弥补学生的认知缺陷。

针对算式（1），可先出示题组：125×（4+8）、125×（4×8），突出乘法分配律与其他运算律的本质区别，使学生清晰认识到：交换律、结合律都是针对一种运算的规律，而分配律是针对两种运算的规律，从而消除分配律与其他运算律的相互干扰。继而出示125×32，启发学生根据题目类型确定解法模式;随后再出示题组：125×32×25、125×25×8，帮助学生摆脱思维定式的影响。

针对算式（2），可先出示题组：27÷821、821÷27;169÷518、518÷169，让学生比较发现题组算式之间的联系与区别。继而出示口答题：如果a÷b=23，则b÷a=？。随后引导学生观察题组：120÷34 — 35和34 — 35÷120，并提问：两个除法算式的被除数与除数分别是什么？商有什么关系？如此逐层揭示，学生自然就明白了上述错误做法的不妥之处。

针对算式（3），可先出示a×b×c，让学生以此模型任意写连乘算式，并说出算式中的a、b、c分别是哪三项。通过练习，学生感知到：这三项可以是一个数，也可以是一个式子。在此基础上，学生再来审题观察20×34+65×10的算式结构，领悟先采用乘法交换律，使之变成200×34+65，再使用乘法分配律比较合适。

如此讲评计算题，能够在一定程度上引导学生改善识别运算信息的审题习惯——变只关注数据特点为先看算式特点，再根据算式特点联想运算律观察数据特点，弥补认知缺陷。

二、在思维生长处“寻根”

郑毓信教授指出，如果我们始终停留于实际操作的层面，而未能很好地实现活动的“内化”，包括思维中的必要重构，就根本不可能发展起任何真正的数学思维。由此我们也可以延伸理解：如果教师评讲试卷时仅仅停留于以题论题，囿于方法的模式化，而未能促进知识的内化，那么即使题目仅仅是转变叙述的方式，学生也有可能一筹莫展。如对于题目“一个正方体容器，从里面量，棱长是5分米。先放入一个不规则铁块，再倒入40升水，铁块被完全浸没。这时测得水深2分米，这个铁块的体积是多少立方分米？”学生一旦被“先倒水，再放物体，然后测量溢出来的水的体积来得到物体的体积”的解题模式囿住思维，就会堕入思考的樊笼，无法找到本题的解法。

可见，试卷讲评时，要在思维生长的关键之处“寻根”，注重引导学生将已有的数学知识按照一定的深度和广度发挥自己的理解，并结合联想、感觉、记忆、思维，将已有的数学知识和数学经验融合，以获得认知的彰显和扩展。

例如，六年级上学期“比”单元教学后的一次检测中有这样一道题目：甲数和乙数的和是44，甲数的35相当于乙数的12，乙数是多少？有如下讲评片段——

师同学们，回想一下，之前学过的哪道题与这道题最相似？

生已知甲、乙两数的和与它们的比，求甲、乙两数。

生我看到“甲数的35相当于乙数的12”，就想到了用假设法来比较甲、乙两数的大小的题来。

师请上来展示给全班同学看。

生（画出线段图，如下页图1）先把甲数平均分成5份，取其中的3份，相当于乙数的12;再画出乙数剩下的一半，所以乙数就是这样的6份。那么，甲、乙两数的比就是5∶6，乙数就是44÷11×6=24。

生假设甲数的35与乙数的12都等于1份，那么甲数可以看成53份，乙数就是2份，所以乙数就是44÷53+2×2=24。

生甲数的35相当于乙数的12，所以乙数应该相当于65个甲数，甲、乙两数的比就是5∶6。

荀子说，人之知为知，己之知为慧。有别于常规的“这道题我们应该怎样解”，这里教师把“之前学过的哪道题与这道题最相似”作为课堂的起始，引导学生把陌生的题目返回到熟悉的“题根”上，帮助学生种下思维生长的第一条“根”，整个题目讲评过程变成了有根基、有时间、有空间、有势头的思维生长过程。学生于其中，不仅得到了结论，更产生了思想和能力。

三、在学习履历中“寻根”

什么是“学习履历”？日本课程专家佐藤学指出：“课程”就是“學习的经验”，是这种经验的轨迹——“学习的履历”。教材是重要的课程资源，是体现课程标准的载体，是学生学习数学、教师教授数学最基本的“学习履历”。那么，我们自然应回到教材中去，剖析学习困惑，还原问题本真，沟通教什么、为何教、怎么教、怎么学之间的联系。

例如，某地区小学毕业考试数学试卷上近年出现的考题：

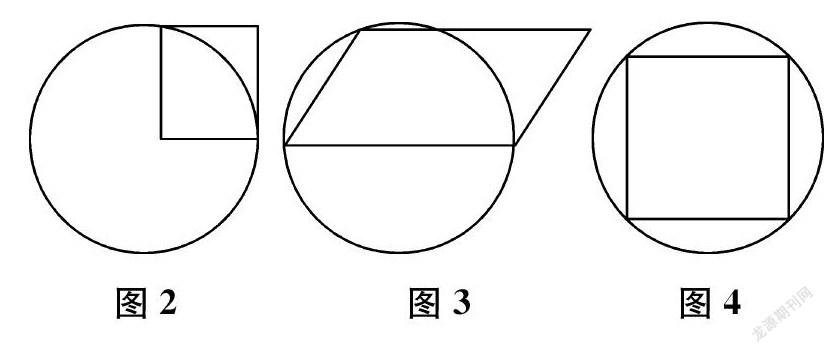
（1）如图2，已知正方形的面积是10平方厘米，圆的面积是（）平方厘米。（2013年）

（2）如图3，如果平行四边形的面积是8平方分米，那么圆的面积是（）平方分米。（2016年）图2 图3图4

（3）如图4，正方形面积是64平方厘米，圆的面积是（）平方厘米。（2017年）

在“圆的面积”教学中，一般通过转化的思路，演绎推理出圆的面积计算公式S=πr2：先建构πr相当于长方形的长，r相当于长方形的宽，再建构出πr2。而有不少教师在应用公式解决问题时，总是习惯性地添上一句：“要求圆的面积，只要知道圆的半径即可。”学生本身在建构公式时对r2的整体感知就偏弱，这样一句话，更是大大强调了r的存在，学生对于r2的整体感知就更差了。在面对以上题目时学生自然会出现困难。

溯“根”至教材。苏教版小学数学教材的思路是：先引导学生通过数方格的方法发现圆的面积与以它的半径为边长的正方形面积之间的近似关系。再将由此获得的结论与下一道例题（利用剪拼转化为近似长方形）中推导出来的公式互相印证，以充分感受圆面积公式推导过程的合理性，加深学生对图形转化方法的体会。完整的学习过程才能催化出深刻的学习体验，促进学生数学能力和素养的提升。