基于数学课堂开放式评估题设计的实践研究

王蒙

摘要：小学数学课程标准指出：为了适应时代发展对人才培养的需要，数学课程还要特别注重发展学生的创新意识。这种意识往往是在解决数学开放式评估题的过程中逐渐培养起来的，开放式问题教学能够促进学生的自主探究和积极思维。本文从问题设计的四个角度重点探讨如何设计开放式的评估题，并结合课堂教学中典型题目的设计案例，详细说明在开放式评估题设计过程中应注意的细节。

关键词：开放式;问题设计;课堂教学

在数学课堂的评估题中，选择题往往适用于评估操作性较强的知识，如小数的乘除法。但对于概念性理解方面的评估，选择题显然不再适用，开放式评估题就比较合适。以下内容笔者将结合大量的设计案例，详细说明在开放式评估题设计过程中应注意的细节。

一、创设生活情境的问题设计，符合数学评估的主要内容

数学是对客观世界数量关系和空间关系的一种抽象。现实生活是学生学习的基础，同样是数学知识的来源。因此，教师在教学中要一方面尽可能让抽象的数学概念借助学具、多媒体、信息化技术等媒介在生活中找到原型;另一方面要设计些开放式问题，能够把学生所学知识去解决日常生活中出现的数学现象，发散学生的思维，提高学生的创新能力。

以三年级上学期区级期末数学测验中的一道题为例：

乐器商店新进了9把小提琴，共花了3600元，售价合理的是（  ）。请你写出理由

A.498元/把B.400把/元C.498把/元D.400元/把

这道题是区教研主任李老师设计的一道开放性选择题，选择D写出合理的理由给2颗星，选择A能够写出售价大于进价的原因得到4颗星。极大部分学生写出的答案是D，给出的理由是3600÷9=400（元/把）。这里为什么选择D选项得到2颗星呢？原因是考查学生对“单价=总价÷数量”的理解和单价的单位运用。李老师在教研活动中指出这道题正确率只有20%左右，考察的目的是学生能否联系实际生活。但总体看来，确实是教师平时只注重书本知识，忽略解决日常生活问题的能力。学生往往习惯去练习直接套用公式、模仿例题的模式，使他们产生死记硬背的积极参与，没有思考问题的想法，不懂得现实生活应用数学知识，这样不利于学生个性的健康发展。因此，对数学问题的选择应该做到真正的开放，这种开放来源于生活，来源于学生自身，让学生熟悉亲切的情感，体验和感受数学的意义和价值。

二、采用适当的提示性语言，避免思维误入歧途

在设计数学开放式评估题时，我们必须重视开放问题的提问方式，并非所有学生能够清楚理解出题者的意图。设置适当的提示性语言可以避免学生思维误入歧途，以促进学生将真实的思维过程暴露出来。

以三年级下“速度、时间、路程”的一道开放式评估题为例，小胖用30分钟的时间走了1500米，距离山顶还有750米，求小胖到达山顶还需要多长时间？

①1500÷750=2，先求出__________;再算 __________，求出__________ 。

②先算__________，求出__________;再算  __________  ，求出__________   。

学生对问题的起点是套用公式速度=路程÷时间，可是一开始就面对方法①，我观察到很多学生是懵掉了，不明白路程÷路程是求什么呢？尽管是思维能力较强的学生也不是一下子写出正确的答案，学生不能准确理解出题者的意图是什么？而方法②学生基本没有问题，能够表达每一步算式的含义。在笔者看来，方法①缺少一定的提示语，多数学生误以为1500÷750=2求的是路程÷路程=2，无法再探究了。实际上我们可以借助画线段图的方法思考或者形象化思考等方式打开思维屏障。

三、把握数学问题的开放度，激发学生的创新意识

我们把数学问题的开放程度叫做开放度，对于事物的“度”，我们总是期望能够带给人们所承受的范围。学生能够根据自己掌握知识水平的不同，选择适合自己解决问题的方法，使得不同层次的学生得到发展，激发学生主动地发现、想象、探索、创新，在解题过程中形成和体验数学思想方法，同时学生从多种不同的角度去思考，思维的方式是发散的，思维带来的结果是创新的。

以“吨与千克”的教学片断为例：

课件出示一幅主题图，上面有牛、熊、马、鹿和一座小桥，并标出各只小动物的体重分别是500千克、400千克、300千克和100千克，小桥上写着“限重1吨”。

师：你们从图中发现什么信息？你能提出什么数学问题？

生1：牛与鹿的体重一共有多少千克？

生2：马比熊的体重少多少千克？

生3：四个小动物的体重一共有多少千克？

……

学生提出了不少要用加减计算的数学问题，但就是没有提出有关“吨”与“千克”之间关系的问题，说明教师在组织教学时忽视对数学本质的关注。没有数学学习内容的本质，就没有数学课的“数学味”，从而导致课堂教学效率下降。我认为这位老师可以这样问：过桥要注意什么？他们能过桥吗？让学生把注意力转向“吨”这个新的知识点，激发学生学习有关吨的知识的欲望。在学生学习吨的知识以后，再引导学生解决：他们该怎样过桥？为他们设计过桥方案。

四、探究有效的开放问题，发展学生的高阶思维

数学课程标准明确指出：数学课程要体现出基础性、普遍性和发展性，数学教育要面向全体学生，实现人人学有价值的数学，人人都获得必须的数学，不同的人在数学上得到不同的发展。因此，教师在进行设计开放式评估题时，一定要厘清每个问题的设计意图，问题内容应包含对思维深度、广度、灵活性等方面的考查，要注重可发展性的问题，留给学生更多思考、探索的空间，从而发挥其有效性。

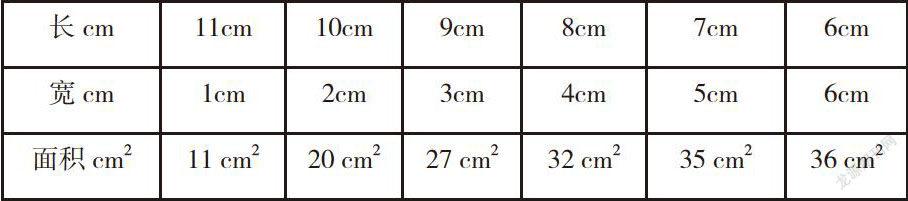
在教学“周长与面积”一课时，笔者设计了一道开放式评估题：小胖想用一根24cm长的铁丝围成一个长方形，请你们来帮他想想办法，如何设计合适的长和宽，求出长方形的面积分别是多少？

小组合作探究，队员拿出准备好的绳子开始实验测量，另一名队员记录结果。在小组成员的合作下完成下表：

师：老师在巡视的过程中看到有些小组没有测量就直接得出数据，你们是怎么得到的？

生：我们根据长方形周长公式推算长与宽之和为12cm，然后从大到小依次考虑的。

师：你们真会思考呀！

师：通过6组数据计算长方形的面积，其实不难发现有什么规律？

生：当长在逐渐减小时，宽在增加，面积也在增加。

师追问：面积最后增加到多少？

生：哦，我发现当长和宽相等时，面积最大。

师总结：当周长不变时，长方形的长和宽的差越小，面积就越大。

五、研究成效

综上所述，一线教师在设计开放式问题时，让素材源于实际生活，体现数学与生活之间的密切联系。在探索和交流学习过程中，学生不仅仅是学会数学知识，还能收获数学思想、数学策略，提升自己的创新能力。

参考文献

[1] Becker ，J P.，Shimada，S. The open-ended approach： a new proposal for teaching mathematics[J]. 1997.

[2] 張奠宙. 总结“数学开放题教学”的中国特色，第二次“数学开放题及其教学”国际学术研讨会论文集[C]. 2003（11）.

[3] 蔡金法，刘启蒙. 课堂评估：如何设计开放式的评估题[J]. 小学数学教师. 上海：上海教育出版社，2017（6）. P4-9.