在小学教学中有效渗透数学思想的策略

徐庆磊 王春丽

《义务教育数学课程标准（2011年版）》指出：“通过义务教育阶段的数学学习，学生能获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验。”“数学思想蕴涵在数学知识形成、发展和应用的过程中，是数学知识和方法在更高层次上的抽象与概括，如抽象、分类、归纳、演绎、模型等。学生在积极参与教学活动的过程中，通过独立思考、合作交流，逐步感悟数学思想。”数学思想是学生形成良好认知结构的纽带，是由知识转化为能力的桥梁，是学生思维发展和数学素养提高的重要因素。因此，要教学中教师要提高对渗透数学思想重要性的认识，在教学的各个环节中渗透数学思想，要使学生能够感悟数学思想、领会数学思想、运用数学思想、创新数学思想。

数学教材包含两条主线，一是数学基本知识，这是一条明线;二是数学基本思想，这是一条暗线。由于数学思想隐藏在教材中，因此，教师在研读教材时要认真分析，理清教材的知识体系和脉络，深入挖掘蕴涵在其中的数学思想，并且要把数学思想的教学纳入到教学目标之中，设计有利于渗透数学思想的教学过程，从而使学生能更好地学习知识、感悟数学思想。

例如，在教学“植树问题”这节课时，通过研读教材可以发现，这一内容主要蕴涵了化繁为简的思想、数形结合的思想、一一对应的思想和模型的思想：将100米的小路栽树问题转化为20米小路的栽树问题进行研究，蕴涵了化繁为简的思想;运用实物图或线段图的方法研究植树问题，蕴涵了数形结合的思想;植树问题中的一棵树对应一个间隔，蕴涵了一一对应的思想;棵树和间隔数的关系，蕴涵了模型的思想。教师在研读教材时，不但要读懂这些蕴涵的数学思想，还要在教学中向学生渗透这些数学思想。教师只有深入挖掘数学思想，并在教学过程中有效设计和实施渗透，才能让学生在潜移默化中感悟数学思想。

通过动手实践、自主探索得到的知识，学生的理解会更深刻，掌握得会更牢固。因此，数学知识的学习要让学生经历知识的探究过程，并在这个过程中渗透数学思想方法，从而使学生在习得知识的同时领会数学思想。

例如，在教学“平行四边形的面积”这节课时，教师可以引导学生自主猜想：“以前我们正经学习过长方形和正方形的面积计算，那同学们能猜测一下平行四边形的面积与哪些条件有关？又该怎么计算呢？”学生根据已有经验猜测：“平行四边形的面积应该和相邻的两条边有关，我猜测平行四边形的面积是用相邻的两条边相乘来计算。”“长方形的面积和长和宽有关，我猜测平行四边形的面积应该与底和高有关，平行四边形的面积可以用底和高相乘来计算。”接着，教师可以引导学生运用准备好的学具探究平行四边形的面积计算公式。学生运用剪拼等方法将平行四边形转化为了长方形，再通过对比平行四边形的底和高与转化后长方形的长和宽的对应关系，求出了平行四边形的面积计算公式。这样，在探究平行四边形的面积的过程中，通过转化思想将新知识转化为旧知识，从而使问题得以解决，对学生独立思考问题获得新知识的能力有很大的帮助。同时，通过类比思想探索出平行四边形的面积计算公式，不仅使数学知识之间建立了联系，也使学生对平行四邊形的面积计算公式的理解变得从容自然。

学生数学知识的掌握以及数学技能的提高主要是通过解决问题来达成的。注重在解决问题中设计能够渗透数学思想的练习，能进一步深化学生对数学思想的感悟，使学生在实际应用中感受到数学思想的价值。

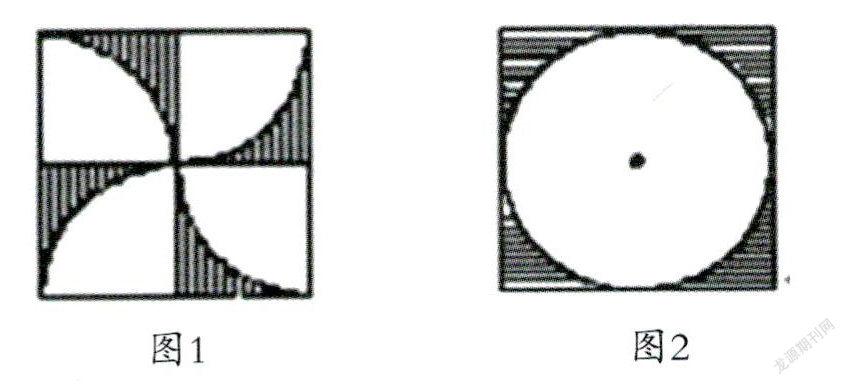
例如，在教学“组合图形的面积”这节课时，教师在课的最后出示了这样一道练习：“求图1中阴影部分的面积。”由于学生在探索平行四边形的面积、梯形的面积、组合图形的面积过程中，对转化思想已经有了深入的感悟，因此，在解决这道题时，很多学生第一时间就想到，阴影部分的面积是四个不规则图形，无法直接求出面积，也无法将其转化为规则图形，那可否将其转化为两个规则图形面积的差呢？学生进一步思考后利用转化思想将图1转化为图2，使阴影部分的面积变成了正方形的面积与圆的面积差，进而解决问题。学生在解决这一问题的过程中，充分运用了转化思想，将未知转化成了已知，简化了解决问题的过程，降低了解决问题的难度，进一步体会了学习和领悟数学思想的价值与意义。

数学思想一方面在教学的各个环节中随处可见，一另一方面散布在不同的内容之中，且同一内容体现出的一般是不同的数学思想，不同的内容又渗透着相同的数学思想。因此，教学中，教师应适时地引导学生对数学思想方法进行归纳、总结、反思，使学生不断升华对数学思想的感悟。这样，不仅有利于学生理解所学知识，构建统领知识的数学思想体系，还有利于提高其自身的数学素养。

例如，在教学“圆的面积”时，教师可以引导学生总结和反思：“同学们，我们学习了长方形的面积、正方形的面积、平行四边形的面积、梯形的面积、圆的面积，在探索这些图形的面积计算公式的过程中，我们主要运用了那种数学思想？你能总结一下吗？”学生在教师的引导下总结了转化思想在探索平面图形的面积中的应用，教师同时可以课件演示几种平面图形的转化关系图（如图3），使学生进一步深化对转化思想的理解，升华列数学思想的感牾。

总之，数学教学不仅是向学生传授数学知识，还要在教学的各个环节中渗透数学思想。在实际教学中，要深入钻研教材，努力挖掘教材中蕴涵的数学思想;采用相应的教学手段，使学生在探究知识的过程中逐步感悟数学思想;进而在应用中深化数学思想，在归纳总结中升华数学思想。

（责任编辑：杨强）