空间向量在立体几何中的应用

孙成琪

摘 要：空间向量知识为几何问题的解决提供了很大的便利。几何问题一般都非常抽象并且复杂，而空间向量知识能够降低几何问题的复杂程度，转化成简单的代数问题，能够帮助人们更好的研究几何问题，因此在高中数学中具有非常重要的地位。本文针对空间向量在立体几何中的应用进行了详细的阐述与分析，将空间向量作为立体几何的解题工具，简化立体几何的题目难度，将几何问题转化为代数问题，解析空间向量如何将立体几何问题变得更具程序性以及可推理性。

关键词：空间向量;立体几何;应用分析

向量知识在立体几何中的应用是数学领域的一场革命，它为几何问题的解决提供了更加清晰的思路[1]。由于向量具有数形结合的特点，能够将几何中的位置问题转化为代数中的数量问题，并且能够依据题目构造出空间直角坐标系，使几何问题得以简化，求解思路避开几何中的复杂位置，清晰、流畅解题[2]。本文通过解析具体例题，对空间向量在立体几何中的应用进行了详细分析。

一、向量知识在几何解题中的作用

当高中数学中引入向量知识后，复数在解题中的意义逐渐被向量取代，向量在数学解题中逐渐占据重要地位[3]。向量的引入使平面与空间问题的解决更加简化，是促进几何问题代数化的重要媒介

向量法分为两部分，一是平面向量，另外则是空间向量[4]。前者能够应用在不等式问题的解答中，同时还能简化证明过程，例如平行问题、共线问题等。还能够解决求值问题，例如距离相向问题等。而空间向量在立体几何中的应用主要包括下面两种类型，一种是位置关系问题，另一种则是度量问题。前者包括线线平行、线面平行等，后者则包括点面距离、角度问题等。向量在立体几何问题的解决中具有明显优势，能够将繁杂的空间几何问题简单化，使其简便易懂。空间向量的引入，还能够彰显数学中数形结合的完美优势。

二、应用向量解决立体几何问题的步骤

应用向量解决立体几何问题主要分为下面几个步骤[5]：第一、创建空间直角坐标系，坐标系的坐标轴尽量选取已经存在的三条线，如果没有这样已经相互垂直的三条线，则需要先找到相互垂直的两条线，再绘制出第三条线，使其分别垂直于这两条线。第二、标注解题时会用到的点的坐标，该步骤一定要仔细认真。第三、写出解题所需的向量坐标，坐标一定是由终点坐标减去起始坐标。第四、应用已经列出的向量坐标解决问题，解决问题过程中一定要运用正确的公式，认真对待运算过程。

三、空间向量在立体几何中的具体应用

空间向量在立体几何问题解决中的应用主要包括以下几个方面：

3.1空间向量对于线面成角问题的解决

线面成角在立体几何中非常常见，但是传统的解题方法非常繁琐，将空间向量引入到此类解题中，能够将线面成角问题变得更加简单，将复杂的问题转变成简易易懂的代数问题。

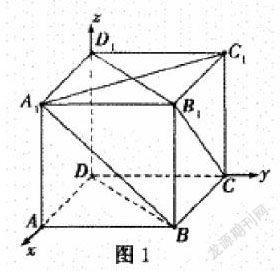
例1：图1正方体中，求对角线A1B与面BB1D1D之间的形成的角。

该题目解决的关键是求出面的法向量，对于题目中已经存在与待求平面相垂直的直线的时候，该直线就可视为面的法向量;对于题目中不存在与待求平面相垂直的直线的时候，则需要假设出待求平面的法向量，通过方程求出法向量，再将其带入到题目中。

3.2空间向量对于面面成角问题的解决

面与面之间的成角问题是立体几何中的常见考察题型，该题型对于初学者而言具有较大的难度，但在引入向量后，难度将得到降低，能够让题目得到较容易的解答。

求两个面之间的夹角往往可将其转化成这两个待求面的法向量之间的夹角问题，创建直角坐标系，运用坐标表示出法向量，再结合图形判断两个平面之间的夹角与法向量之间夹角的关系，求出法向量之间的夹角，进而求出两个平面之间的夹角。

3.3空间向量对于点面距离问题的解决

点与面之间的距离问题也是立体几何中的常见题型，由于立体几何抽象性强，此类题型的解题难度较大，引入向量知识之后，解题过程简化，解题效率将得到大幅提高。

例3：图3的正方形ABCD边长为1，PD垂直于平面ABCD，PD=1，E为AB的中点、F为BC的中点，则点D与平面PEF之间的距离为多少？

解题分析：创建图3中的空间坐标系，则下列点的坐标分别为：D（0，0，0），P（0，0，1），E（1，1/2，0），F（1/2，1，0）。

求解点与平面之间的距离的时候，有些点在平面中的射影位置不好寻找，则需要运用向量知识解决此类问题，向量的引入能够减少辅助线，降低解题难度。

空间向量在立体几何中的应用，不仅能够解决线面成角问题、面面成角问题以及点到平面之间的距离，同时还能够解决异面直线之间的距离、线线平行问题、面面垂直问题等，这些问题共同的特点是题目均存在一定的难度，且频繁出现在高中数学的试卷中，但传统的解题方法解决此类问题非常繁琐，引入空间向量后，能够将复杂的结合问题转变成简易易懂的代数问题。

结束语

总而言之，向量知识在立体几何中的应用对于降低复杂的空间几何问题具有非常重要的意义。在几何问题中合理应用向量知识，将空间问题中的位置关系转变成数量关系，减少辅助线的应用，进而使几何问题得以简化、使问题更加简单。向量知识的应用，向人们展示出一种新的解题思想与解题方法，它突破了传统的解题思想，同时也为今后探求新的解题思想提供了有效的促进效果，培养我们的空间想象能力以及探索创新能力。

參考文献

[1]马彦彬.向量在立体几何中的应用研究[J].考试周刊，2018（40）：83.

[2]韩子萱.空间向量在立体几何中的运用[J].中华少年，2018（02）：285.

[3]马建华.高中数学空间向量在立体几何中的应用[J].考试周刊，2017（81）：87.

[4]王千迎.空间向量在立体几何中推广与运用[J].课程教育研究，2017（38）：140.

[5]孙平.掌握空间向量神器决战高考立体难题——例析空间向量在立体几何中的应用[J].数学教学研究，2017，36（03）：57-62.