三角函数在高中数学中的解题应用

摘 要：在高中数学的知识体系中，三角函数扮演着重要的角色，几乎贯穿了我们整个高中阶段的数学学习，而且在各类题型中都有应用之处。但三角函数部分的知识点比较琐碎，需要记忆的公式也较多，这就给我们的学习造成了不小的障碍。本文就三角函数在高中数学中的解题应用进行了初步的探讨，希望对同学们有所帮助。

关键词：三角函数;高中数学;解题方法

有许多同学对三角函数“谈之色变”，因为这部分知识点多，公式多，题型多，而且没用什么可以循规蹈矩的方法，所以学起来很吃力。要弄懂三角函数，还是要从其基本概念入手，理清知识脉络，做好分类，探索出自己的解题套路，而那些纷繁复杂的公式只是我们解题的工具而已，这样一来相信三角函数也将不再是高中数学学习中的难点了。

一、三角函数的知识脉络

学习三角函数，我们首先需要对角有一个新的认识，高中阶段我们所接触的角已经不再是0～360°的范围了，而应为任意角，即（）范围内的所有角，同时引入弧度制的概念，这就要求我们要有一个周期角的思想。在学习角度概念的时候，我们要借助两个好帮手，即象限角与单位圆，三角函数的定义也由此而来。三角函数也是基本初等函数，是以角度（弧度）为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。高中数学里我们需要掌握的三角函数为正弦（sin），余弦（cos）和正切（tan），其各自的定义分别对应于单位圆上相应线段的比值，而函数名之前的符号则遵从“一全正，二正弦，三两切，四余弦”的规律。在此基础上，还要熟练掌握同角三角函数的基本关系式，即商数关系和平方关系，同时要将诱导公式的规则熟稔于心，牢记口诀“奇变偶不变，符号看象限”，其中奇、偶指的是的奇数倍或偶数倍，变与不变是指函数名称的变化。

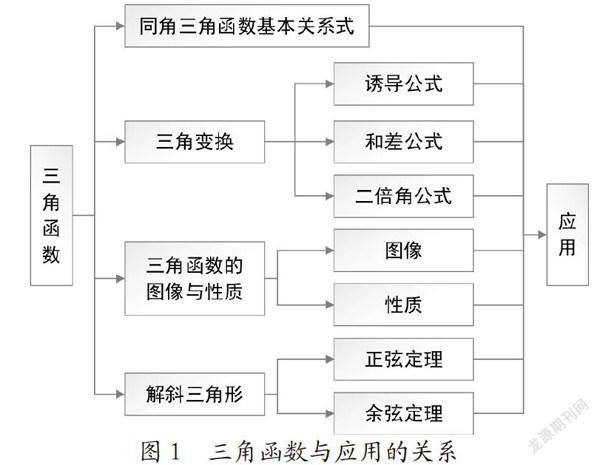
在掌握了三角函数的基本概念之后，我们就要开始“变换”了。三角函数之所以成为高中学习的重点，同时成为很多同学学习的难点，很关键的一点就是在于其变换形式的多样性，且各类三角函数之间都可进行变换，这就需要我们先理清它们的关系，并做好分类，建立连接三角函数与解题应用之间的桥梁，如图1所示。

二、三角函数的性质与函数图象

三角函数虽然在形式上存在一定的特殊性，但究其本质还是一种函数，所以我们完全可以用学习函数的思想来学习三角函数。既然是函数，那么它就必然有单调性、奇偶性、周期性等函数性质，当然也可以做出函数的图像。

三角函数既然也是一类函数，那么对其性质的研究也应按照普通初等函数的学习方法来进行，除了掌握三类基本的三角函数的性之外，还需掌握，及的相关性质。

对于三角函数的图象，最基本的应掌握三类三角函数的原始图象并能用“五点法”作图，其次是掌握三角函数的平移变换的方法，建立数形结合的思想，学会运用函数图象结合单位圆解题。

三、三角函数的解题应用

有了以上的知识体系，我们就需要融会贯通的将这些知识点运用到解题中去。这里我总结了三类题型的解题策略供读者参考。

1.三角函数式的化简与求值

在面对三角函数式的化简与求值问题时，我们需要运用同角三角函数的关系式，即和，同时合理使用诱导公式。

化简与求值的题目，题干往往比较长，有的同学看到密密麻麻的三角函数名就无从下手，这时候就需要一定的化简策略，當我们看到题目中同时存在“弦”和“切”时，就应考虑两个方向，要么化弦，要么化切，因为只有当函数名为同类时，才方便我们进行使用积化和差、和差化积、倍角公式等手段进行进一步的化简与求解。

2.三角函数的性质

正如之前所述，三角函数是一类初等函数，在作为考题考察其性质的时候，题目的类型与普通初等函数的类型相类似，不同点则在于对三角函数周期性和奇偶性的考察，而在我看来，所有死记硬背式的记忆方式都不如画一个图像来的直接、有效，通过数形结合我们可以很直观的得到三角函数的诸多函数性质，不论是定性的讨论函数的周期性、奇偶性，还是定量的求得函数的单调区间，我们需要掌握的其实只有最基本的正弦、余弦和正切的图像，然后拿题目所给的变形后的图像与之作对比，即可得到我们想要的结果。

3.三角函数的图象

我们可以通过待定系数法解决由三角函数图象求三角函数解析式的问题，通过数形结合的方法，图象中的最大值或最小值对应A，图象的周期对应，再由图象中的具体点来确定的值，但要注意，的值并不唯一，要通过限制其取值范围来确定的确切值。

四、总结

高中数学中三角函数部分历来都是考试的重点，其知识点多，题型丰富，给同学们在学习的过程中造成了一定的困难。但只要掌握了三角函数的知识脉络，合理运用公式与图形图象，总结出每一类题型的解题方法，相信三角函数将不再是高中数学学习中的难点。

参考文献

[1]魏大铮.浅析高中数学三角函数解析技巧[J].科技风，2017（03）：241.

[2]朱作炜.关于高中数学三角模块的教学研究[D].湖南师范大学，2016，57（3）：45-46.

作者简介：李想（2000.08——），性别：男，民族：汉族，籍贯：陕西省榆林市府谷县府谷镇，西安市西铁国际中学高2019届M2-3班学生。