挑战性任务促进学生思维发展

许秋咏

摘要：在数学课堂教学中，教师设计挑战性的学习任务，能够优化课堂教学氛围，转变学生的学习方式，驱动学生深度学习，促进学生的思维发展，提升学生的数学思维能力。本文从“核心性、开放性、深度性、综合性”四个维度来阐述如何设计学习任务，促进学生思维的发展。

关键词：挑战;任务;思维;发展

近几年，笔者所在校数学教研组深入挖掘小学数学教材，采用“同课异构”的模式进行课堂实践、研究探讨。在研讨中，有所感悟：同样的教学内容，设计的理念不同，给老师、学生的感受也是完全不同。

案例对比，引发思考

如教学《圆柱的表面积》时，陈老师的教法是教师讲解圆柱的表面积含义，动画展示圆柱侧面展开图;小组合作探究侧面积公式，思考展开的图形和圆柱体之间的关系。林老师的教法是完成一个制作任务：每人用卡纸仿照所带的茶叶罐做一个茶叶罐模型;同桌互相说一说制作方法。

从以上两个个案例对比后发现：陈老师的设计只注重知识与技能的教学，学习起来，波澜不惊，显得枯燥。而林老师的设计具有一定的挑战性，更能激发起学生探究的热情，也需要一定的时间去思考和讨论，能够产生个性化的答案，为学生的深度合作交流提供了更广阔的空间，使不同思维水平的学生得到了不同程度的发展。因此，笔者认为，高效优质的课堂是教师围绕教学重难点，提供给学生具有挑战性的学习任务。

设计问题，发展思维

数学课堂的核心问题，即每节课中能起主导作用，能引发学生积极思考、探究的问题。为了让学生的思维更加灵活，教学中要舍弃过多的教学铺垫，不要急于给学生思维定向，以免学生的思维受到限制。当他们面对问题的时候，需要他们利用已学过的思想方法和知识，自己想办法“搭梯子”，探索解决问题的思路。

以“平均数”一课为例，许多教师会按部就班地出示主题图，让同学解决问题：平均每人收集了几个水瓶？然后告诉学生“平均每人收集的个数”就是这一组数据的“平均数”。其实，如何让学生更深刻地体会到“平均数”的价值，让学习更有深度，可以直接给出一个学习任务（课件出示学生收集矿泉水瓶的统计图）。

甲队：小红、小兰、小亮、小明

14、   12、   11、   15

乙队：冬冬、婷婷、 晶晶

11、    18、   13

接着，老师抛出核心问题：“我们要把‘环保小卫士’的奖状颁给他们其中一队，给哪一小队合适？说说理由？”同学们积极发言，有的认为该比总数，有的认为该比大数，还有的认为人数不一样，无法比较，应该去掉一个。老师说：“同学们的想法很多，下面以小组为单位，根据老师发的统计图，想一想有没有更公平的方案？”于是，学生们围绕这个问题，展开了积极的探究活动，终于想出了合理的方案。有的用“移多补少”的方法，有的用“先总后分”的方法，在解决问题的过程中，学生深刻地体会到平均数的作用和求平均数的方法。

核心问题的设计，能够更加充分地体现学生的主体作用，让他们基于自己的理解去尝试着解决问题。探究过程中碰到的困难、考虑问题不周产生的错误，都会让他们积累丰富的经验，使自己分析问题、解决问题能力得到提升，思维得以发展。

开放性问题解读

开放性问题，即教师为学生营造一个开放的学习环境，呈现的问题条件不完备，答案多元，学生解决问题的方法具有差异性。众所周知，当今社会需要的是活泼、开朗、富有个性的人才。教学时，教师呈现开放性问题，有利于培养学生思维的创造性。当然，在某些特定的案例中经常会出现同样的问题，由于个人的理解不同，引发了不同层次的思考，呈现出了不同的答案和不同的表达形式，如有的学生喜欢画图，有的学生喜欢计算，有的学生喜欢文字叙述。但在交流分享中，学生明白了为什么相同的问题，答案却不一样。

开放性问题给学生留下了巨大的挑战空间，鼓励学生提出与众不同的看法，有利于培养学生的创造性思维，拓展学生的视野，让不同层次的学生都有所收获，品尝胜利的果实。

究原理，发展思维

数学课堂所提的问题，既要让学生明白“是什么”，更要理解清楚“为什么”。鼓励学生凡事多问几个“为什么”，不光知其然，更要知其所以然。每个人只有透过现象，发现事物的本质，思维才能越来越深刻。

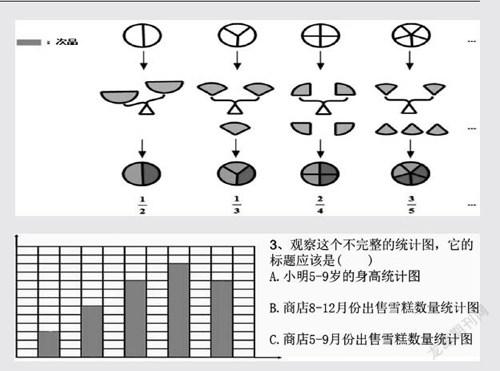
以“找次品”一课为例，多数老师引导学生按照3个、4个、8个、9个、10个的顺序逐步地猜想、操作、验证，得出“每次平均分成3份，称的次数最少”的规律，学生从动手操作实践中初步懂得了找次品时一定要把全部物品尽量平均分成3份，才能最快找到次品（即：找的次数最少且能保证找到）。

而有挑战性学习任务的课堂，执教老师就要巧设“富有挑战性的学习任务：为什么要平均分成3份，其中的奥秘是什么？”才能够带领学生继续探索。這个挑战性问题一提出，课堂的气氛又活跃起来，学生对挑战性问题兴趣盎然。教学中，尽量让学生用各种手段进行说理，若全班同学都无法突破这个教学难点时，老师应该有意识地引导学生观察（如图）。

因为称的零件个数是有限的，所以再利用课件把许多物品汇成一个集合圈，平均分成2份、3份、4份、5份……称一次后，学生发现次品所在的范围分别变成了 、 、 、 ……通过分数大小的比较，把集合圈平均分成3份，次品所在的范围最小，这就是平均分成3份的原因。

深究问题的原理，让学生的学习不仅仅停留在表面的观察和发现，更注重把握事情的本质规律，在这个过程中，他们的思维得到了再一次的提升。今后，遇到问题，学生视角就会更宽广，分析更加深刻，不易被假象所迷惑。

挑战性学习任务效果

综合性问题，是考验学生知识应用，整合信息能力的问题。数学课的巩固练习必不可少，但是很多数学老师设计的练习片面、单调，只针对新教的知识点，这种练习只能让学生机械地掌握新知识。综合性问题信息量大，往往能打破学生的思维习惯，从新的角度提出问题，学生练习时不仅能够运用所学的知识，还需要结合自己的生活阅历才能解决，具有一定的难度。

例如，教学四年级的“统计与概率”一课，老师呈现了这样的一道练习题。学生顺向思维题目做多了，偶尔来一道逆向思维综合题，对他们来说，更值得挑战。老师让学生独立思考后，在小组里面说说自己的想法，学生很开心地讨论起来了，最后派代表上台发言。有的说：“绝对不可能是A，因为身高怎么可能会长着长着就变矮了。”有的说：“B也不行，11月怎么可能卖雪糕卖得最多，太冷了，谁要吃。”还有的说：“答案应该是C，8月最想吃雪糕了。”所有学生积极地参与到讨论之中，他们分析得头头是道，在你一言我一语中，问题逐渐明朗起来。

挑战性的学习任务，打破了枯燥、机械、简单的数学教学模式，这样的数学课堂有思维层次、有生活味道、有探索价值，逐步培养了学生解决问题的综合能力。

参考文献

[1]吴存明.设计挑战性任务让学习真正发生[J].新课程研究，2018（02）.

[2]葛绍飞.合作学习任务的设计研究[D].华东师范大学，2015.

[3]翁淑燕.数学教学如何体现新课程理念[D].新课程（教师版），2006（4）.

（作者单位：福建省厦门市翔安区教师进修学校附属小学）