究其惑,寻其解
徐志刚
摘 要:解析几何是高中数学教学当中的重难点内容,也是高中数学教学当中的重要组成部分之一。解析几何要求学生在解题的过程当中,能够以平面直角坐标系为基础,充分利用数形结合方法,通过代数方式来解决问题。除此之外,高中解析几何的教学方法要求数学教师具备更高的专业素养和能力。在进行解析几何的教学之前,教师首先应充分理解有关解析几何的相关知识和深刻内涵,并充分考虑到学生的接受能力与学习能力,选择最合适的教学模式,提升学生的逻辑思维能力。
关键词:解析几何;数学教学;高中数学
【中图分类号】G633.6 【文献标识码】A 【文章編号】1005-8877(2019)19-0003-02
在新课改后,有关部门将解析几何纳入了重点教学内容。学生在刚刚开始学习有关解析几何的知识时,首先应该掌握圆锥曲线和圆的方法以及在平面直角坐标系当中怎样用方程来表达直线。在掌握了这些代数的基础知识之后,学生才能借助其开展对于几何问题的进一步研究,进而深刻领会数形结合思想的重要性。在此基础之上,学生便可以熟练掌握方程与曲线之间的关系,并熟练运用三角函数以及平面向量等知识点。只有做到了上述几点,才能更好地为通过解析几何知识解决实际问题奠定基础,进而提高高中学生的数学学习效率。因此本文将浅谈笔者对于解析几何教学的一些感悟。
1.高中解析几何教学中的数学思想
(1) 运用坐标法解决数学难题。高中阶段的几何思想主要体现在运用坐标法解决数学难题上,而要高效运用几何思想应该做到以下几点:第一,正确选择坐标轴;第二,利用代数与曲面以及曲线之间的关系和本质明确表达题意;第三,借助代数知识解答几何问题。在解题的过程当中坐标的选择是其中的重点内容。若能选择适当的坐标轴,可以在很大程度上简化学生的分析过程与计算过程。其中应该注意的是,选取不同的坐标轴并不会改变图形本身的性质。以几何图形椭圆来说明,例如,一个圆经过椭圆x2/16+y2/4=1的三个顶点,且圆心在x轴的正半轴上,则求该圆的标准方程。这种题目有坐标法是最好的求解方法,首先根据椭圆的方程可以求出三个顶点的坐标分别为,(4,0)、(0,-2)、(0.2),并且圆心在x轴正半轴,设圆心的坐标为(a,0),则圆的半径为4-a,可以得到(4-a)2=a2+22,那么可以解出a=3/2,所以得到椭圆的方程为(x-3/2)2+y2=25/4。在此题中,主要是通过坐标之间的关系来建立等式,利用圆的半径均相等来建立恒等式。这三种建立坐标系的方法,横轴的位置并无区别,主要在于纵轴位置与原点位置的选取。在教学时教师可以分别使用这三种方法建立直角坐标系,并计算,引导学生感受这三种方法在计算过程当中的差异,进而帮助学生深刻领会到利用直角坐标系来解决问题的巧妙作用。
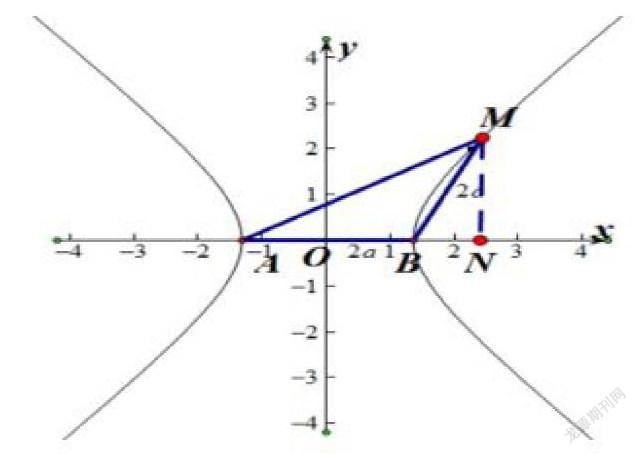
(2)运用数形结合来解决数学难题。高中数学解析几何首先要借助代数初步了解几何图形的表达方式通过将图形反映到坐标系上,然后将图形转换成代数问题进行解决,也就是说计算出图形的坐标方程。例如,两条平行直线可以通常两个方程来求解,判断解的情况,进而判断直线是否平行,从而将几何问题转换为代数问题;再有,通过计算代数式,理清代数与几何图形之间的关系;最后,将所得出的答案转化成为题目所需的几何问题的答案。例如,求解离心率的问题,已知A,B为双曲线E的左右顶点,点M在E上,三角形ABM为等腰三角形,且顶角为120°,则求双曲线E的离心率。解题时,首先要有清晰的解题思路,然后通过图形以及坐标的方式来求解答案。本题可以通过设双曲线的方程为x2/a2-y2/b2=1(a>0,b>0),如下图所示,AB=BM,角ABM=120°,过点M做MN垂直于x轴,垂足为N,在直角三角形BMN中,BN=a,MN= a,可以得到M点坐标为(2a, a),代到双曲线方程得到c2=2a2。所以求得离心率e=_________________ .
2.高中数学解析几何教学中的主要问题
(1) 高中生缺乏较强的数形结合能力。高中生刚刚接触复杂、抽象的几何问题,因而大多数高中生都不具备较强的数形结合能力,他们在解决几何问题的时候无法充分发掘题目当中的隐藏条件,进而无法正确画出题目所需的几何图形。多数学生在多次读题后仍然无法正确画出图形,进而无法顺利证明题目所需的条件或者无法求出题目所需的数值。
(2) 高中生缺乏较强的逆向思维能力。在学习有关解析几何的内容时,要求学生具备几何图形当中的信息转化成为代数表达式的能力。这项工作看似只是将相同的条件用两种不同的方式表达出来,实则条件的转换会直接影响到解题的过程与结果。我们在高中阶段常说的逆向思维是指以代数知识为基础,根据题目所给的条件推算出代数关系式。而高中学生才刚刚接触到有关几何的知识,因而大部分高中生并不具备逆向思维的能力。正是由于逆向思维能力的缺失为学生学习有关解析几何的知识带来了极大的阻碍。
(3)高中生不具备较强的计算能力。在高中解析几何当中,需要将图形语言转化成为数学语言,且计算量较大。而高中教师在教学的过程当中大多数都过于重视学生思维模式的训练,却忽视了对于学生计算能力的培养,因而大多数高中学生都不具备较强的计算能力。因此在解析几何教学过程当中常常会出现学生思维正确,但是最终计算结果错误的现象,极大降低了学生解题的正确率。
3.高中数学解析几何中的教学方法
(1)贯穿数学文化,提升学习兴趣。在高中数学过程中,老师要灵活运用课本,不能将其作为教学依赖,应丰富其课堂形式,从而培养学生对数学学习的兴趣。现阶段,在高中教材当中有关解析几何的教学内容容量较大。比如,在学习“平面解析几何初步”这一章节的内容时,要求学生能够同时掌握根据圆解方程、根据直线解方程以及建立空间直角坐标系等多种解题方式。教师在进行解析几何教学时应巧妙地将数学史融合在其中,这样不仅能够提升学生的解题与学习能力,还能够培养学生对数学的喜好。比如,老师在讲解坐标系时,可以将数学史穿插到课堂授课当中,可以给学生讲讲与坐标系相关的数学史,引起学生学生兴趣。老师可以在讲解该章节的内容之前先查阅一些有关笛卡尔的事迹以及思想。在正式上课之前先给学生普及这些小知识数学故事,从而激发学生对解析几何的学习热情与兴趣。
(2)强调坐标地位,熟练建立坐标。高中学生在学习有关解析几何的内容时,平面直角坐标系的建立会在其中起到非常重要的作用。这是因为建立直角坐标系可以将代数和几何这两个毫无关系的数学元素结合起来,取长补短,进而有效解决数学难题。此外,高中学生最先是通过直角坐标系来理解几何图形的,因而教师在进行解析几何教学时应强调坐标系的重要性,教师在教学时可以从以下几个方面入手:首先,教师在讲述该章节的内容时一定要强调坐标系对于解析几何的重要性,并明确建立直角坐標系和解题的具体步骤,帮助学生明确思路,建立解题框架。一是,学生在拿到题目之后应该先审题,然后根据题意和几何图形的性质建立合适的直角坐标系,并借助方程式或者是坐标轴将几何图形中的条件用代数式表达出来。二是,学生要用课本上所讲到的代数知识解答代数问题,并得出正确的答案。三是,学生应合理分析代数结果,最后将其与几何图形的基本性质相结合,得出最终的结论。
其次,教师在讲授解析几何章节内容时应注重培养学生的数形结合思想,并引导学生使用数形结合的思想解决几何问题。只有这样学生在遇到复杂的几何问题时才会明确思路,通过建立直角坐标系来解决该类题型,进而让学生领会到使用坐标法解决几何问题的简易型和高效性。比如,在证明三角形或者四边形的性质时,单纯地依靠几何当中的定理与性质是很难得出正确答案的,这个时候就需要学生建立直角坐标系,采用代数的方法来证明,可以极大提高解题效率。例如,若双曲线的方程为x2/a2-y2/b2=1(a>0,b>0)的一条渐近线呗圆(x-2)2+y2=4的弦长为2,求曲线C的离心率。在求解本题时,可以通过坐标系来求解,可以在坐标系中画出圆的方程,然后通过一直关系来构造等式。由几何关系可以得到x2/a2-y2/b2=1(a>0,b>0),双曲线的渐近线方程为bx+ay=0或bx-ay=0,圆心的坐标为(2,0),到渐近线的距离为 ,则点(2,0)到渐近线bx+ay=0的距离为2b/c= ,则c2=4a2,,所以求得离心率e为2
(3)注重引发思考,提升思考能力。数形结合思想是在解析几何教学当中常用的思维模式,但高中学生想要培养数形结合的思维模式若是仅仅依靠教师的课堂讲解是远远不够的,更重要的是学生应该树立主动思考的意识。学生在仔细审题并独立思考之后提取题目当中抽象化的知识点,然后借助所提取的这些信息解决几何问题,并通过练习大量的几何难题培养属于自己的独特的思维模式和解题思路。因此教师在讲述解析几何章节内容时应正确引导,培养学生独立思考的能力,并将教材当中的知识点转化成问题,根据教学进度逐条提出这些问题,引导学生自主思考、寻求答案,最终找到解题的新思路、新方法。
(4)关注学生特点,安排针对教学。从学生本身来说,每一道数学题都会包含多个不同的数学知识点。若是将这些知识点区分开来,分条讲解,学生大多都能熟练掌握并学会运用,但若是将这些知识点综合在一起,学生将会无法区分进而出现解题障碍。所以高中教师在开展数学教学的时候不能强行灌输,而应结合实际情况,根据学生的学习能力与接受能力,按照顺序依次将这些问题抛出来,进而培养学生解决数学难题的综合能力。
4.结束语
综上所述:在高中数学教学的过程当中解析几何占据着异常重要的地位。由于本文篇幅有限,并不能详细列出所有的教学方法,还有很多教学方法是笔者未写道的、未发现的,还等着高中数学教师在日常教学当中不断创新、深入探索。为了进一步提高高中数学的教学质量,帮助学生更好地掌握解析几何这个难点内容、提高高中学生的数学学习能力、应用能力,高中数学教师还应不断完善自己,提高自己的专业能力与素养,提升自己的数学能力为解析几何教学提升贡献自己的力量。
参考文献
[1]卢彩欢.解析几何的实践教学法—高中数学教学方法引导论[J].中国科教创新导刊,2012(12)
[2]龙正武.例谈平面解析几何教学效率的提高[J].数学教学,2011(06)
[3]谢正,李建平.空间解析几何教学改革的一些探讨[J].赤峰学院学报(自然科学版),2014.01(08):215-217
[4]张丽娟.结合学生实际水平的解析几何课程初探[J].甘肃科技,2015.07(06):79-81
[5]石勇国,赵思林,彭家寅等.解析几何课程教学改革探索[J].内江师范学院学报,2013.04(09):70-73
[6]卢春林.析初中数学教材中的例题与习题的重要性[J].数理化解题研究(初中版),2014(10)
[7]张艳.数形结合思想在高中数学教学中的应用研究[J].中国校外教育,2016(11)
[8]张讲道.2010年江苏省高考题第18(III)题的别解与拓展[J].数学教学,2011(05):46-48

