基于ADAMS的多刚体动力学简化建模与仿真

王 坤，邢海军，徐梦超，张林浩

基于ADAMS的多刚体动力学简化建模与仿真

王 坤，邢海军，徐梦超，张林浩

(石家庄铁道大学机械工程学院，河北 石家庄 050043)

应用多刚体动力学理论在ADAMS软件中对复杂模型进行简化建模与仿真，解决复杂模型在ADAMS中建模过程繁琐、仿真过程计算效率低等问题。首先对简化建模方法的多刚体动力学理论进行了分析；然后提出了基于ADAMS简化建模的具体方法，着重研究了使原模型和简化模型中心主转动惯量、中心惯量主轴连体基方向相同的数学方法；最后，将该简化建模方法应用到过山车单车模型上，并对仿真结果进行对比分析。结果显示基于ADAMS的多刚体动力学简化过山车模型与原模型的仿真效果基本相同。该简化建模方法能有效提高复杂模型在ADAMS中的建模效率和仿真的计算效率。

ADAMS；多刚体动力学；简化建模；运动仿真；过山车

ADAMS是使用广泛的虚拟样机软件，用于机械系统的运动学及动力学分析，例如大小型机械设备、机械传动装置、机器人、游乐设施等的虚拟仿真。但由该软件建立虚拟样机模型时，过程非常繁琐，效率远不及Solidworks、Creo等三维实体建模软件。因此，目前采用ADAMS对机械系统进行运动学及动力学仿真时，常常先在三维设计软件中建立模型，再将其导入到ADAMS软件中进行虚拟仿真[1-2]。如对过山车的运动过程进行虚拟仿真时，需先在三维设计软件中建立实体模型，然后将模型另存为.x_t格式后导入ADAMS软件中，再进行建立各零件之间的约束副、施加载荷等操作，最后通过仿真运动过程，得到动力学与运动学仿真结果[3]。

上述方法对于简单模型非常方便，但对于包含零部件数量繁多的复杂设计模型，在ADAMS软件中对其进行编辑和仿真时会出现诸多问题。典型的问题有：如果采用Model Name导入，则需要在每个零件之间重新建立约束副[4]，不仅由于零件过多耗费大量的时间，而且会出现位置捕捉不准确、方向设定不精确等问题；如果采用Part Name将相对固定的刚体导入后，则需要重新赋予其密度，由于相对固定的各刚体并非密度完全相同，因此质量属性会与原模型不一致，只有通过一系列计算重新给模型附加等效的质量属性，否则会影响仿真结果的正确性。同时，上述方法还存在导入时间长、占用内存大、仿真用时长等问题。

为解决上述问题，本文根据多刚体动力学理论，提出基于ADAMS的简化建模方法。该方法的原理是采用形状简单的刚体代替原模型复杂刚体，保证简化刚体与原模型刚体的质量、中心主转动惯量、质心位置、中心惯量主轴连体基的方向相同；各刚体之间的约束副、模仿载荷以及仿真观测点的位置等特征与原刚体一致。从而实现简化模型与原模型仿真结果基本相同，并且建模和仿真效率会有很大提高。本文以过山车单车的简化建模和运动学仿真分析为例，对仿真结果与原模型进行对比，结果表明该建模方法是可行的。

1 简化建模方法的原理

刚体一般运动可分为平动和绕质心的转动，应用质心运动定理和对质心的动量矩定理[5]，可建立刚体一般运动的微分方程:

(1) 平动方程

其中，为刚体质量；a，a，a分别为质心的加速度在，，方向上的分量；，，分别为作用在刚体上外力的主矢量在，，方向上的分量。

(2) 对质心的转动方程

其中，J，J，J分别为刚体在，，轴上的中心主转动惯量；，，分别为刚体转动角速度投影在，，轴上的分量；，，分别为刚体转动角加速度投影在，，轴上的分量；，，为刚体所受外力对质心的力矩分量的代数和。

由式(1)和式(2)可知，刚体在外力、外力矩作用下，其在某时刻的速度、加速度、角速度、角加速度等参数的变化，即机械系统的刚体运动、动力学情况决定于刚体的质量、中心主转动惯量、质心位置、中心惯量主轴连体基的方向及所承受载荷的大小，而与刚体的形状、密度无关。因此可以用满足上述条件的简单均质几何体，如长方体、圆柱体、球体等对称几何体代替原刚体进行建模仿真，提高建模仿真效率，其为多刚体动力学简化建模方法的原理。

2 建立简化模型的方法

2.1 满足质量属性相同

将原模型中相对固定的各个部分分别看作为不同的刚体，查看每个刚体质量属性得到其质量、质心坐标、中心惯量主轴的方向、中心主转动惯量等参数。在三维设计软件或ADAMS中建立简化刚体，并通过如下方法实现简化刚体与原刚体的质量属性相同。

2.1.1 满足中心主转动惯量、质量、质心位置相同

设原刚体质量为，中心主转动惯量为J，J，J，通过中心主转动惯量公式[5]与质量公式反求出一个均质简单几何体的各形状要素。以长方体为例，其密度、长、宽、高可通过式(3)得到

其中，，，分别为长方体在，，轴方向的长度。

这也就实现了该长方体与原刚体的中心主转动惯量、质量相同。并可根据原刚体的形状不同，采用不同的均质简单几何体代替，如原刚体的中心主转动惯量中有2个数值相同时，简化刚体可为圆柱体、圆环体等；当中心主转动惯量均相同时，简化刚体可为正六面体、圆球等形状。当然，如果简化刚体的几何参数多于方程数量，需要事先确定某些几何参数以满足与方程数量相同。

按照原刚体的质心坐标移动简化刚体，使得两者的质心坐标一致。

2.1.2 满足中心惯量主轴连体基的方向相同

刚体在三维设计软件(以Solidworks为例)的质量属性中，惯性主轴I，I，I即表示中心惯量主轴连体基的方向余弦，即

其中，，，分别表示基础坐标系的，，轴方向；ʹ，ʹ，ʹ分别表示刚体中心惯量主轴连体基的，，轴方向；cos(ʹ)为基础坐标系轴与刚体中心惯量主轴连体基轴的夹角余弦值。根据机构学中刚体的齐次坐标旋转变换知识，刚体的方向余弦矩阵[6]为

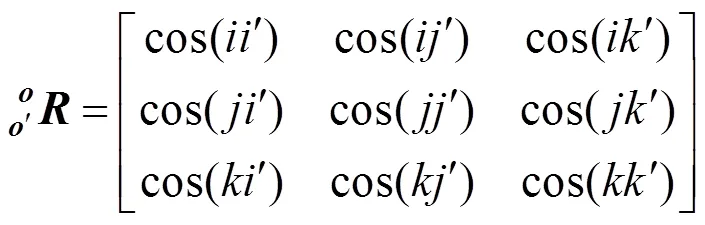
刚体的方向余弦矩阵是通过刚体的旋转矩阵相乘得到的[6]

其中，，，分别为刚体绕，，轴旋转的欧拉角；，分别为cos，sin，由于刚体的旋转变换是相对于基础坐标系进行的，所以刚体的旋转顺序是先绕轴旋转角，再绕轴旋转角，最后绕轴旋转角。

令矩阵

根据式(4)和式(5)，可得

根据式(6)和式(8)，得出

通过式(4)和式(9)列方程组，即可求出刚体旋转的欧拉角，，。使简化刚体在基础坐标系下以质心为旋转中心先绕轴旋转角，再绕轴旋转角，最后绕轴旋转角，即可满足其中心惯量主轴连体基的方向与原刚体相同。

综上所述，若以长方体代替原刚体，只需针对式(3)~(9)编制通用计算程序，即可得到替代各种复杂结构形状的长方体的质量属性，高效率完成建模。

2.2 约束副的建立

为了模仿2个刚体之间的运动副，首先在三维设计软件中的原模型上确定各个约束副的位置、类型以及所约束的运动情况；然后在ADAMS中简化模型的相同位置建立MARAKER点；最后在各简化刚体之间建立运动副，其位置位于上述新建MARKER点。运动副的类型及所约束运动与其所代替的2个原刚体之间的运动副的类型及所约束运动情况相同。

2.3 载荷的施加与仿真观测点的建立

为了模仿载荷，在简化刚体上建立MARAKER点(Add to part)，该点在简化模型上的相对位置与原模型上施加载荷的相对位置相同。施加载荷时，载荷作用在该MARAKER点上，载荷的大小、方向与原模型一致。

为了观测仿真完成后的计算结果，特别是某些点的轨迹、速度及加速度，在简化刚体上建立若干MARAKER点(Add to part)，其在简化模型上的相对位置与原模型上仿真观测点的相对位置相同。

3 在过山车单车上的应用举例

3.1 原模型质量属性的分析

过山车单车模型图是在三维设计软件Solidworks中建立的，如图1所示。将相对固定的零件看作一个刚体，可将单车分为4个独立的刚体，即前车架、座椅架、连接架、后车架，如图2所示。

图1 过山车单车整体模型图

(a) 前车架(b) 座椅架 (c) 连接架(d) 后车架

以前车架为例，表1为通过查看各独立刚体的质量属性，得到的各刚体质量、重心坐标(质心位置)、惯性主轴(中心惯量主轴连体基的方向)以及惯性主力矩(中心主转动惯量)等参数值。

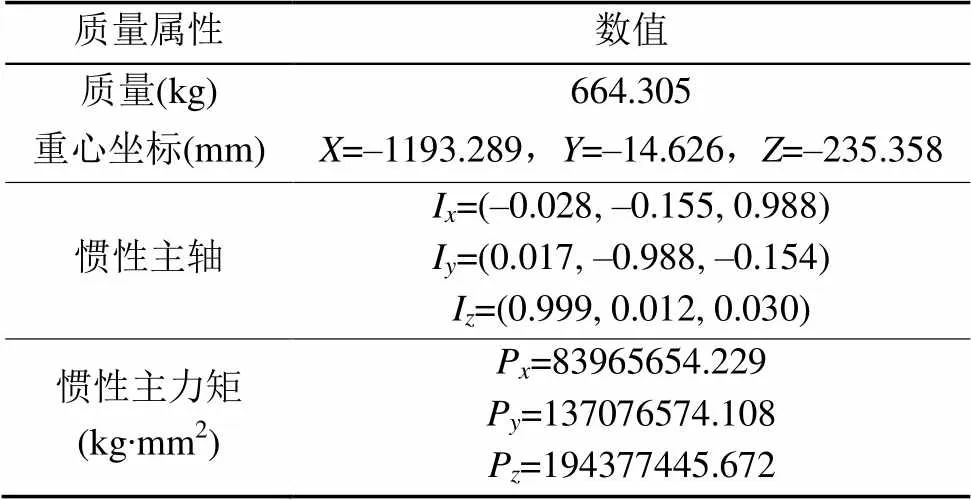
表1 前车架质量属性

3.2 简化刚体的建立

采用均质长方体作为简化刚体，通过表1中原刚体的质量属性，利用式(3)和式(9)求得各简化刚体的密度、外形参数以及位姿参数，见表2。

表2 各简化刚体参数

图4 过山车轨道轴测图

3.3 约束的建立

通过分析可知过山车单车原模型包含3个约束副，分别是前车架与座椅架之间的球副，座椅架与连接架之间的转动副(绕轴)，连接架与后车架之间的转动副(绕轴)，如图1所示。根据原模型中约束副坐标，分别在ADAMS的简化模型图中的相同坐标位置建立MARKER点，并创建与原模型相同类型、所约束运动情况相同的约束副，如图5所示。

同时，过山车前后车架上的车轮与轨道之间共存在6个点线接触关系，通过查看原模型中车轮与轨道接触点的坐标，在简化模型中的相同位置建立MARKER点(Add to part)，并与轨道建立点线接触关系，如图5所示。

图5 简化模型约束副位置图

3.4 载荷的施加与仿真观测点的建立

3.4.1 载荷的施加

原模型施加驱动力的位置位于前车架上，在ADAMS的简化模型图的相同坐标建立MARKER点(Add to part)，并在该点添加单向力，采用STEP函数定义单向力的变化：

STEP(time,57,(ABS(VM(MARKER_32)-1500)-(VM(MARKER_32)-1500))*2.11E3,57.1,0)

同时根据原模型的运动情况在简化模型上添加摩擦力、制动力等[7-8]。

3.4.2 仿真观测点的建立

通常过山车运动学的观测点设在座椅上方600 mm处[9]，在ADAMS的简化模型图的相同坐标处建立MARKER点(Add to part)，且该点建立在座椅架上，本文以左侧人为例。同时分别建立该点的特征函数：运行速度，加速度在方向上的分量A，A，A。

3.5 仿真结果对比分析

原模型将过山车单车分为4个刚体(图2)，采用Part Name导入ADAMS，如图6所示。通过一系列计算得出原模型质量属性后，修改导入ADAMS模型的质量属性与原模型一致，并进行添加约束、载荷等操作。

图6 过山车单车ADAMS模型图

原模型与简化模型采用相同的仿真步长0.02，仿真时间97 s。对比原模型与简化模型观测点的速度，加速度在，，方向上的分量为A，A，A，图7为对比图及局部放大图(实线代表原模型，虚线代表简化模型)，截取其中60.0~60.5 s时刻内观测点数值进行观察对比，见表3。

通过图7可见，简化模型与原模型中观测点的特征图基本相同。从图7的局部放大图和表3中可以看出，原模型观测点的数值落后简化模型观测点数值约0.04 s，其原因为：

(1) 在计算简化模型质量属性过程中由于截断误差的存在，造成简化模型与原模型质量属性存在很小的偏差。

(2) 原模型在导入到ADAMS软件后，需要重新赋予其质量属性，重新赋予的质量属性也会因为截断误差造成微小的偏差。

因此，由于截断误差的存在，导致原模型与简化模型的计算结果不完全一致，但误差很小，对之后的动力学、结构学分析影响可以忽略。不过，根据刚体动力学理论，如果简化模型和原模型的惯性特性完全一致，那么仿真结果必定是完全相同的，即动力学方程与几何形状是无关的。综上所述，简化模型可以替代原模型进行运动仿真。并且在同一台电脑下，原模型的仿真持续时间为127 s，而简化模型的仿真持续时间仅用32 s (显示仿真过程)，可见简化模型的仿真效率远高于原模型。

表3 原模型与简化模型观测点某段时刻数据对比表

4 结 论

采用ADAMS的多刚体动力学简化建模的方法，可以解决复杂模型零件过多、建立约束过程耗时繁琐的问题，避免导入的模型质量属性与原模型不一致的弊端。同时，由于模型结构简单，占用内存很小，能有效提高建模和仿真效率，并能得到与原模型基本一致的仿真结果。针对刚体数更多、运动更为复杂的机械系统，只要根据需要建立相应的简化刚体、约束副，同时提高计算过程的精确性，其仿真结果的正确性是可以保证的。因此，该方法可以应用于各种复杂模型的建模与仿真。但是，由于简化模型与原模型的外形不一致，该方法不适用于带有表面接触的动力学问题，例如仿真齿轮间的啮合、车辆的碰撞等问题。

[1] 马峰, 张华, 胡晓莉. 基于ADAMS的液压挖掘机建模与仿真分析[J]. 机床与液压, 2014, 42(9): 130-132.

[2] 刘俊利, 徐建, 孔秀平. 基于ADAMS的采煤机虚拟样机建立与运动学仿真[J]. 煤炭技术, 2018, 37(5): 222-224.

[3] 吴纯君. 三环过山车车体二维设计与仿真研究[D]. 马鞍山: 安徽工业大学, 2016.

[4] 张晨, 崔彧青. 基于SolidWorks和ADAMS的齿轮传动装置建模与仿真方法[J]. 机械工程师, 2017(2): 79-80.

[5] 哈尔滨工业大学理论力学教研室. 理论力学-Ⅰ[M]. 北京: 高等教育出版社, 2009: 260-276.

[6] 张春林. 高等机构学[M]. 北京: 北京理工大学出版社, 2005: 19-25.

[7] 郑建荣, 汪惠群. 过山车虚拟样机的建模与动态仿真分析[J]. 机械设计与研究, 2004, 20(2): 74-77, 9.

[8] 于泽涛. 基于虚拟样机技术的过山车仿真研究[D]. 大连: 大连理工大学, 2009.

[9] 国家市场监督管理总局, 中国国家标准化管理委员会. GB8408-2018大型游乐设施安全规范[S]. 北京: 中国标准出版社, 2018.

Simplified Modeling and Simulation of Multi Rigid Body Dynamics Based on ADAMS

WANG Kun, XING Hai-jun, XU Meng-chao, ZHANG Lin-hao

(School of Mechanical Engineering, Shijiazhuang Tie Dao University, Shijiazhuang Hebei 050043, China)

In ADAMS software, multi-rigid-body dynamics theory is applied to simplify the modeling and simulation of complex models, which is used to solve the complicated modeling process in ADAMS and the low computational efficiency of the simulation process. Firstly, the multi-rigid body dynamics of the simplified modeling method is analyzed. Then the specific procedure of simplified modeling based on ADAMS is put forward. The present study attaches great importance to a mathematical method that enables the central principal moment of inertia and the principal axis of central inertia of the original model and the simplified model to be of the same orientation. Finally, the simplified modeling method is applied to the roller coaster bicycle model, and the simulation results are compared and analyzed. The simulation results show that the simplified dynamic roller coaster model based on ADAMS is basically the same as the original model. This simplified modeling method can effectively improve the modeling efficiency of complex models in ADAMS and the computational efficiency of simulation.

ADAMS; multi-rigid body dynamics; simplified modeling; motion simulation; a roller coaster

TP 391

10.11996/JG.j.2095-302X.2019040733

A

2095-302X(2019)04-0733-06

2019-02-28；

定稿日期：2019-05-14

王 坤(1986-)，男，河北邢台人，硕士研究生。主要研究方向为机械设计及理论等。E-mail：kunan0526@163.com

邢海军(1967-)，男，河北深泽人，教授，博士，博士生导师。主要研究方向为振动控制、结构分析等。E-mail：412261035@qq.com