空间观念怎样测评

◇邵 钦

怎样的试题可以测评出学生的空间观念？空间观念测评的核心是什么？测评空间观念水平高低的依据又是什么？本文试图通过对空间观念测评的相关试题分析与解读，为空间观念测评的内容提供一些案例，为空间观念测评的核心提供一些角度，为如何测评出学生空间观念的水平提供一些思路。

一 空间观念的测评可以围绕“四条线索”展开

“图形的认识”“测量”“图形的运动”以及“图形与位置”是图形与几何领域学习的四条线索。因此，对空间观念的测评内容也应围绕这四条线索逐一展开。

（一）围绕对图形特征认识的过程开展测评。

例题1：在自制的陀螺上点一个黑点，陀螺在旋转时黑点可以形成一个圆形的痕迹（如图1）。

图1

小明也自制了几个陀螺，并点上了黑点（如图2，“×”标出的是插入火柴棍的地方）。

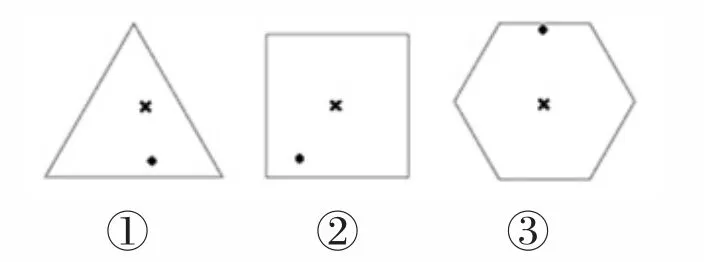
图2

以上哪个陀螺在旋转时黑点可以形成一个圆形的痕迹？下面说法正确的是（ ）。

A.①②③都不能形成

B.只有③能形成

C.只有②和③能形成

D.①②③都能形成

这是一道有关圆的认识的试题，此题测评的重点是：学生能否抓住圆的特征，通过想象理解圆的概念。这一问题的解决对学生具有一定程度的挑战性，因为无论在哪幅图中，陀螺旋转时黑点所形成的痕迹都无法直接看到，学生的一般策略是在头脑中将这三幅图分别找到定点和定长，然后进行旋转，想象出黑点所形成的轨迹。所以本题实际上是借助制作陀螺这样一个素材，测评学生对圆的特征的认识，特别是学生头脑中对圆的表象的认识和理解。

（二）凭借对图形大小的理解开展测评。

如何依托图形测量的内容将测评的视角由度量和计算转为评价学生的空间观念呢？下面的例题则是利用这一内容进行空间观念测评的一个案例。

例题2：用12 个小正方体拼摆成一个立体图形，如图3所示。至少移动其中（ ）个小正方体可以将这个立体图形变成一个体积不变的长方体。

图3

A.1 B.2 C.3 D.4

本题测评的是学生对长方体体积的认识，长方体的大小是由长、宽、高三者决定的，也正是这三者构成了三维空间中的长方体。题目给定了长方体的大小，学生需要通过观察和想象得到一个符合要求的长方体图形。

在解决这一问题时学生通常要通过已知的长方体的体积想象或推断出其长、宽和高，再进行小正方体的移动；或是通过在头脑中先对小正方体进行逐一地移动，当移动成为长方体时，回忆移动的块数，再比较几个方案移动块数的多少。因此，这道题实际上是依托对长方体体积的认识这一素材，测评学生是否能够对小正方体进行正确的移动，从而测评出学生的空间观念。

（三）依托图形运动的生活素材开展测评。

图形的运动在小学阶段主要包括对称、平移、旋转和相似，在现实生活中存在着大量的这些运动现象，这些现象是测评空间观念时很好的素材。利用这些素材，既可以测评学生的空间观念，又能够帮助学生动态地认识我们生存的空间。

例题3：张叔叔开车回家，在路口等红灯时，从车的后视镜里看到了后面的公交车，如图4所示。根据图中信息，可以判断出公交车是（ ）路。

A.28 B.58 C.82 D.85

本题是对现实生活中对称现象的测评。学生在解决问题时要将后视镜中的数在头脑中还原为实际的车牌，当然，一些学生通过将试卷翻过来看，推断得到正确答案也不失为一种策略，这一策略也正体现了他们能够将头脑中想象的过程，用现实中的直接操作行为进行验证，从而得到结果。

（四）突出相对位置关系的理解开展测评。

图形的位置是以多种方式刻画图形（或物体）的位置并应用这些方式确定位置及位置关系为主要内容，发展学生空间观念的。课标中也就这一内容提到了“想象出物体的方位和相互之间的位置关系”这一空间观念的具体表现。下面的例题则是结合这一内容的一道题。

例题4：下面关于“中心广场”的位置，描述正确的是（ ）。

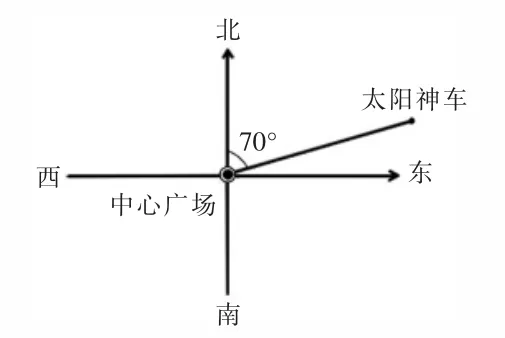
图5

A.中心广场的位置在太阳神车的东偏北70°的方向

B.中心广场的位置在太阳神车的西偏南70°的方向

C.中心广场的位置在太阳神车的南偏西70°的方向

D.中心广场的位置在太阳神车的北偏东70°的方向

这道题从方位的角度确定和描述位置，是在相对位置关系理解的基础上，进行学生空间观念的测评。本题对学生的空间观念具有很大的挑战性，因为，对于中心广场与太阳神车这两个地点来讲，我们可以用任意一个地点为观测点去描述另一个地点的位置，当观测点发生变化时，另一地点与观测点的相对位置关系就会发生变化。题目给出了从中心广场观测太阳神车，太阳神车在观测点的北偏东70°的方向，依据这个关键信息，学生要想象出两个地点的相对位置关系，从而判断出从太阳神车观测中心广场的位置。

二 空间观念测评的关键是想象和推理

学生空间观念的形成与发展，应通过观察、操作、想象、推理、表达等活动展开，因此，对空间观念的测评也可以着眼于这几个要素来做。那么，怎样的试题能够将“想象”或者“推理”测评出来呢？

例题5：李明沿图6中所示的粗实线和粗虚线剪开正方体纸盒，然后将纸盒各面向外展开，那么与展开后的图形形状相似的是（ ）。

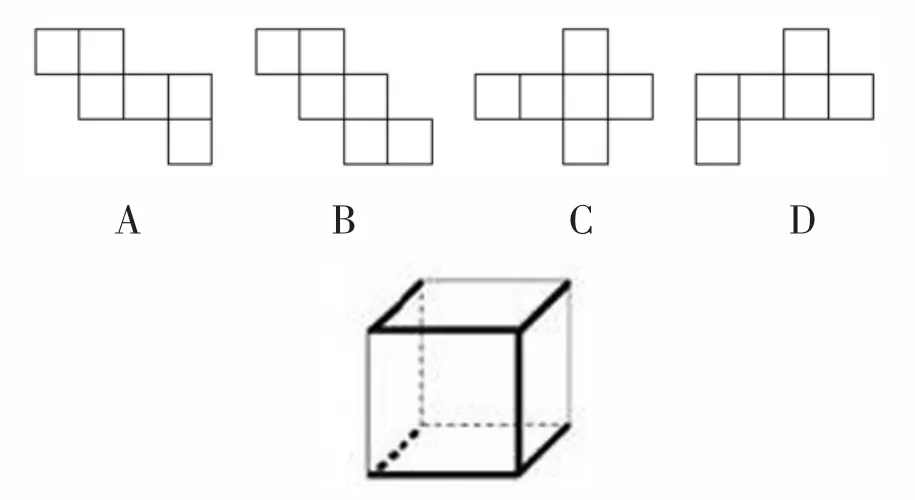
图6

本题四个选项均为正方体的展开图，学生无法靠之前对展开图的记忆进行选择，也无法靠现场操作立体图形或平面图形寻找答案。在解决问题的过程中，学生需要通过观察，并在头脑中想象将正方体盒子沿棱剪开的过程，思考剪开后面与面之间的关系，得到正方体对应的展开图。

例题6：淘气用一些大小相同的小正方体搭出了一个立体图形，并从不同方向观察后画出了下面的三幅图（如图7）：

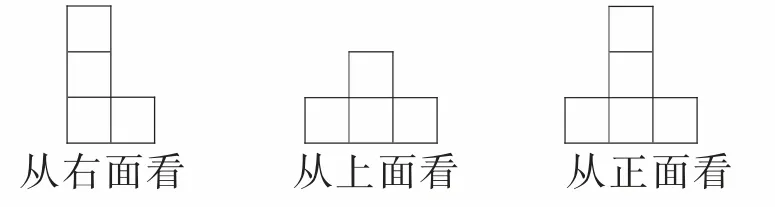
图7

淘气所搭出的立体图形用了（ ）个小正方体。

对于这道题，学生需要根据三视图进行立体图形的还原，并得到正确拼搭块数。解决这一问题对学生的思维有较高的要求，学生需要结合情境进行非形式化的推理。例如，他们需要多次在头脑中进行类似“如果……那么……”的尝试，需要有条理地在头脑中对三视图进行逐一的操作，从而得出正确的结论。整个问题的解决突出经历“提出假设—得出一个结论—证实或否定这一结论”这样循环往复的一个过程。

通过上面的两道题可以发现，题目应以四条线索中的某一内容为载体，以想象、推理作为解决问题的途径和测评的最终目标进行设计。尽量避免学生通过现场制作一个符合题意的物品，进行简单操作就能解决的问题，突显出想象和推理在解决空间与几何问题中的价值和意义，测评出学生的空间观念。

三 测评空间观念的水平要关注学生的表现

每个人空间观念的水平不同，因此我们需要寻求较为科学和有效的方式，以测评学生空间观念的水平。根据学生的作答情况给予不同层次的评价是开展有效测评的方式之一。

例题7：玩具厂要将一批长方体木块原料切割成长方体小积木，如图8所示，这样的一块长方体木块原料最多可以切割出几块长方体小积木（不能拼接）？可以写一写、画一画，说明你的切割方案。

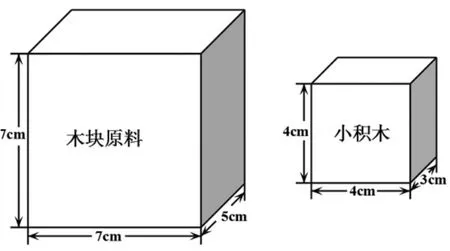
图8

本题所传递的不仅仅是单纯的体积测量问题。具体来讲：首先，测量的标准有“特定的规格”；其次，这种特定规格不能通过更小的标准拼接得到。因此，学生解决这一问题必须依靠空间想象，并且对其中的小长方体要不断进行旋转摆放，同时需要把这样的想象过程与想象后的结果通过写一写、画一画的方式表达出来。

由于题目本身具有一定的开放性，学生在完成切割小积木的任务时，因切割方案不同，所呈现的结果也不同，反映出的空间观念水平也不尽相同。因此不能简单地对学生进行评价，需要制定出较为合理的空间观念水平的评价指标。

首先，将能否借助图形在头脑中进行旋转来解决问题，作为评价空间观念水平高低的关键性指标。

其次，依据学生解决问题时表现出的一些基本特征，进行相关水平的层次划分，如表1所示：

表1

再次，为了更准确地了解学生空间观念的水平，需要将表1中的特征进行进一步外显，外显后的各水平具体描述及学生的表现情况如下：

水平0，切割的块数为1～5 以外的数，且无法直观表达出切割方案。

水平1，用算式计算出5 块，没有用直观的方式表达出切割的方案，或直观表达了切割出1块的方案，或只写出了4 块而没有切割方案的说明。学生的典型解答如图9所示。

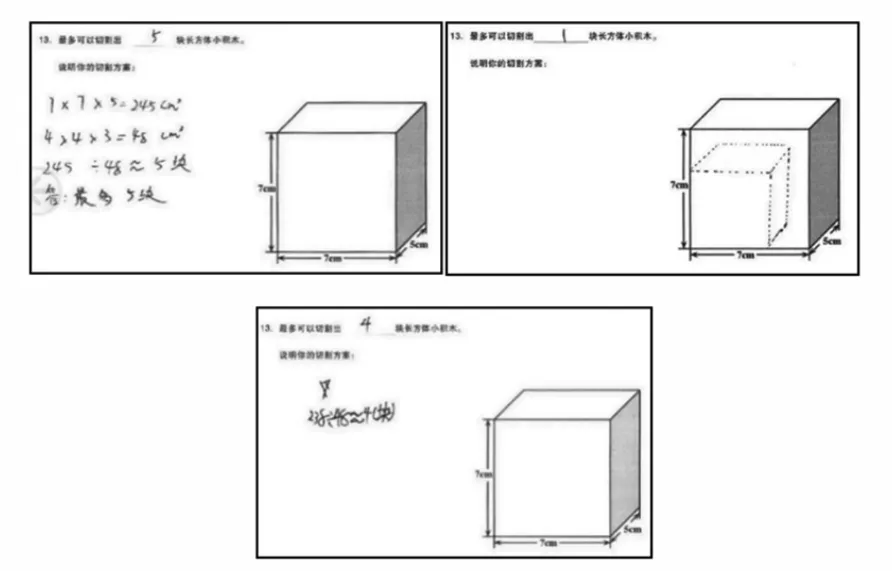
图9

水平2，借助直观表达的方式，正确表达出切割方案为2 块、3 块的结果，或借助直观表达的方式，表达出的切割方案为4 块，但无法实现这种方案。学生的典型解答如图10所示。

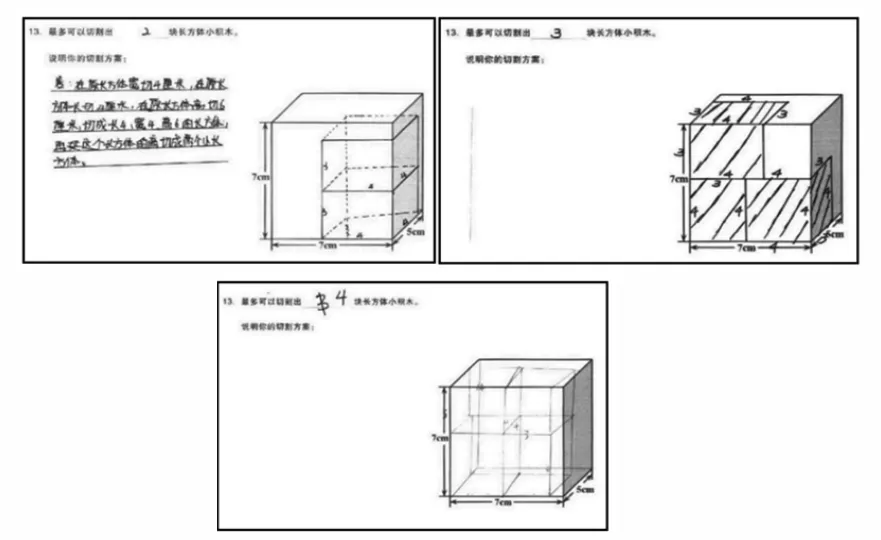
图10

水平3，借助直观表达的方式，正确表达出切割方案为4 块的结果。学生的典型作答如图11所示。

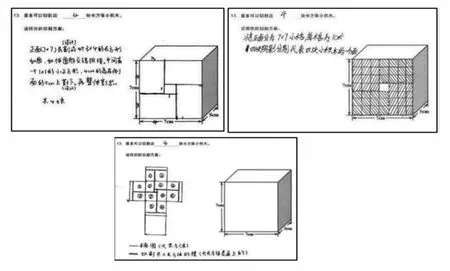
图11

至此，依据学生的解答情况划分出了本题空间观念的不同水平表现，这样使得对学生空间观念的测评更为具体和详尽，同时也使得空间观念水平评价具有了一定的可操作性。