基于集成组合预测模型的隧道大变形预测研究

(重庆工商职业学院,重庆 401520)

近十几年，在我国经济快速发展的带动下，公路工程得以迅猛发展，截至2017年末，我国公路总里程达477.35万km，较2016年增加7.82万km，其中，隧道工程共计有16 229处，总计长度约15 285.1 km，包含特长隧道902处，长隧道3 841处，较2016年增加1 048处。由此可见，隧道工程在公路建设中的比重较大，加之我国地域广阔，地质条件复杂，使得隧道工程事故日益增加，其中，隧道大变形就是一种常见的隧道施工灾害，因而开展隧道大变形规律研究具有重要意义[1-2]。目前，已有诸多学者开展了相应的隧道大变形研究，如魏来等通过统计国内外多个隧道大变形事故，分析了软岩区的隧道大变形机理及力学特性，并针对性地开展了防控措施研究，对实际工程具有重要意义[3]；高文工等基于现场监测数据，开展了隧道大变形预警研究，为现场灾害防治提供了依据和借鉴[4]；高发征采用三维数值模型分析了隧道大变形过程的力学行为，并开展了防治对策研究[5]；张云鹏、王军龙等基于隧道大变形现场监测数据，开展了隧道大变形预测研究，有效掌握了隧道变形发展趋势[6-7]。上述研究虽取得了相应成果，但较少涉及隧道大变形预测，或预测模型较为单一，难以保证预测结果的稳定性。为克服前述单一预测模型的缺点，常瑶以尖点突变理论和趋势波动分析为基础，综合研究了隧道大变形预测规律[8]；任庆国则利用粒子群算法优化BP神经网络的模型参数，构建了隧道大变形的组合预测模型，并得到了良好的预测精度[9]。上述组合模型验证了集成组合预测思路在隧道大变形预测研究中的适用性，且相对于单一预测模型具有更高的准确性，进而有必要对其进行进一步的研究。

近年来，变形预测方法日益成熟，神经网络、自回归滑动平均模型、灰色模型等都在岩土领域得到了广泛应用，但隧道大变形受多种不确定因素、偶然因素的作用，使得单一预测模型难以保证预测结果的精度及稳定性。因此，本文基于多种单项预测模型，构建了混沌优化的集成组合预测模型，并利用通省隧道大变形事故为工程实例背景，开展了该模型的有效性检验，以期为类似工程的变形预测提供一种新的思路。

1 基本原理

总体思路主要包含两个阶段：集成预测模型的构建阶段和预测结果准确性的验证阶段。其中，前一阶段主要包括单项预测模型的筛选和混沌优化组合模型的构建；后一阶段主要是利用M-K检验评价隧道变形的发展趋势，以佐证预测结果的准确性。根据论文思路，将各阶段的基本原理及过程分述如下。

1.1 单一预测模型的筛选

由于不同预测模型的原理存在一定差异，进而有必要对各类单项预测模型进行筛选，且各单项预测模型应遵循互补性原则。根据相关文献的研究成果[10-12]，可知ARMA模型、三次指数平滑模型及GM(1,1)模型在隧道变形预测中均具有较高的预测精度，且各模型的优缺点如表1所示。通过对比各模型的优缺点，得出其相互之间具有较强的互补性，因此，可将上述3种模型作为本文组合预测的单项预测模型。

表1 各预测模型的优缺点对比Tab.1 Comparison of the advantages and disadvantages of each prediction model

1.2 混沌优化组合模型的构建

传统组合预测方法多是采用单一组合手段或从多个组合方法中选取最优组合预测结果，均未考虑基于初步组合预测结果的递进组合预测分析，未能充分发挥不同组合模型的优势。因此，本文提出在初步组合预测的基础上进行递进组合预测，并利用混沌理论进一步优化预测结果的残差序列。因此，该阶段可分为3个过程，即初步组合模型的构建、递进组合预测模型的构建及混沌优化预测，将三者的实现过程分述如下。

1.2.1初步组合预测模型的构建

组合方法可分为线性组合和非线性组合两类，且为了充分验证各类组合方法的适用性，本文对两种组合方法均进行了研究，且将线性组合组合方法确定为方差权值法和误差权值法，即分别以各单项预测结果的方差、误差为评价指标，对其进行归一化处理，所得归一化值即为对应的组合权值，且整个过程的组合权值始终不变。同时，将非线性组合预测模型确定为BP神经网络和支持向量机，其网络结构均是以各单项预测结果为输入层，对应节点处的实测值为输出层，进而实现非线性预测。

1.2.2递进优化预测模型的构建

该阶段可进一步细分为两个过程：包括组合系数(即权值贡献系数)的求解和混沌理论的优化，两个过程的具体步骤可细分如下。

(1) 组合系数的求解。预测模型的预测精度可利用多个指标进行评价，且可根据评价指标的属性将其划分为两类，即精度指标和稳定性指标。其中，精度指标包括均方根误差和平均绝对误差，而稳定性指标包括方差和标准差。同时，基于各评价指标，提出利用权值贡献系数来确定各初步组合模型的递进组合权值， 如图1所示。权值贡献系数的确定过程为：先将各初步组合模型的相应评价指标进行归一化处理，并求得各初步组合模型在各评价指标条件下的累加值；随后，将各初步组合模型的累加值再进行归一化处理，得到的归一化值即为权值贡献系数[13]。

图1 综合组合系数的求解示意Fig.1 Schematic diagram of comprehensive combination coefficient solving

(2) 混沌理论的优化。需要指出的是，不论何种组合模型，均难以完全描述评价序列的发展趋势，这是因为预测样本本身就存在一定的测量误差，而这些误差往往具有混沌特性。因此，本文提出利用混沌理论优化前述递进组合预测结果的残差序列，即利用混沌理论先对残差序列进行相空间重构，主要包含如下过程[14]。

① 若递进组合预测结果的残差序列为{εi,i=1,2,…，n}，可将其向m维相空间进行映射，即：

ψi=[εi,εi+τ,…,εi+(m-1)τ]T

(1)

式中，m为嵌入维数；ψi为第i个相点；τ为延迟时间。

② 根据上式可知，要实现相空间重构，需先求得嵌入维数和延迟时间，其中，利用关联维数C(λ)求解嵌入维数m，且关联维数可表示为

(2)

式中,H(*)为Heaviside函数；N为相点个数，且N=n-(m-1)τ；λ为给定常数。

关联维数与λ之间存在对数线性关系，即维数d(m)为

(3)

当λ值在一定范围内时，d(m)值与m值存在递增关系，且d(m)值趋于稳定时，对应的m值即为嵌入维数。

同时，利用偏复自相关法求解延迟时间，在求解过程中，延迟时间的相关函数如下所示：

(4)

式中,ε′为残差序列均值。

随着τ值变化，延迟时间的相关函数与τ值呈递减函数，当C(τ)值等于1-1/e时，对应的τ值即为延迟时间。

③ 基于前述参数求解，再利用Lyapunov指数法实现残差序列的预测，即以ψi为预测中心，得到它与最近相邻点ψl间的距离为

d=min‖ψi-ψj‖=‖ψi-ψl‖

(5)

式中，ψi为残差序列预测中心点；ψl为预测中心点的相邻点。

当d值最小时，预测模型的表达式为

‖ψi-ψi+1‖=‖ψl-ψl+1‖eλmax

(6)

式中,λmax为Lyapunov指数的最大值。

根据上式可知，利用ψl可推导出εi+1，进而实现残差序列的优化预测。

1.3 预测结果准确性的验证

为验证集成预测模型的有效性，本文提出利用M-K检验来判断隧道大变形发展趋势，并将其结果与集成预测的外推预测结果进行对比[15-16]。在M-K检验过程中，若零假设H0表示各检验样本分布相同且相互独立，而备择假设H1是双边检验，那么对i≠j，且i,j≤n，则xi和xj具有不同分布，进而可求得初步统计量S为

(7)

同时，初步统计量需服从方差Var(S)=[n(n-1)(2n+5)]/18且E(S)=0的正态分布，进而得到标准统计量Z：

(8)

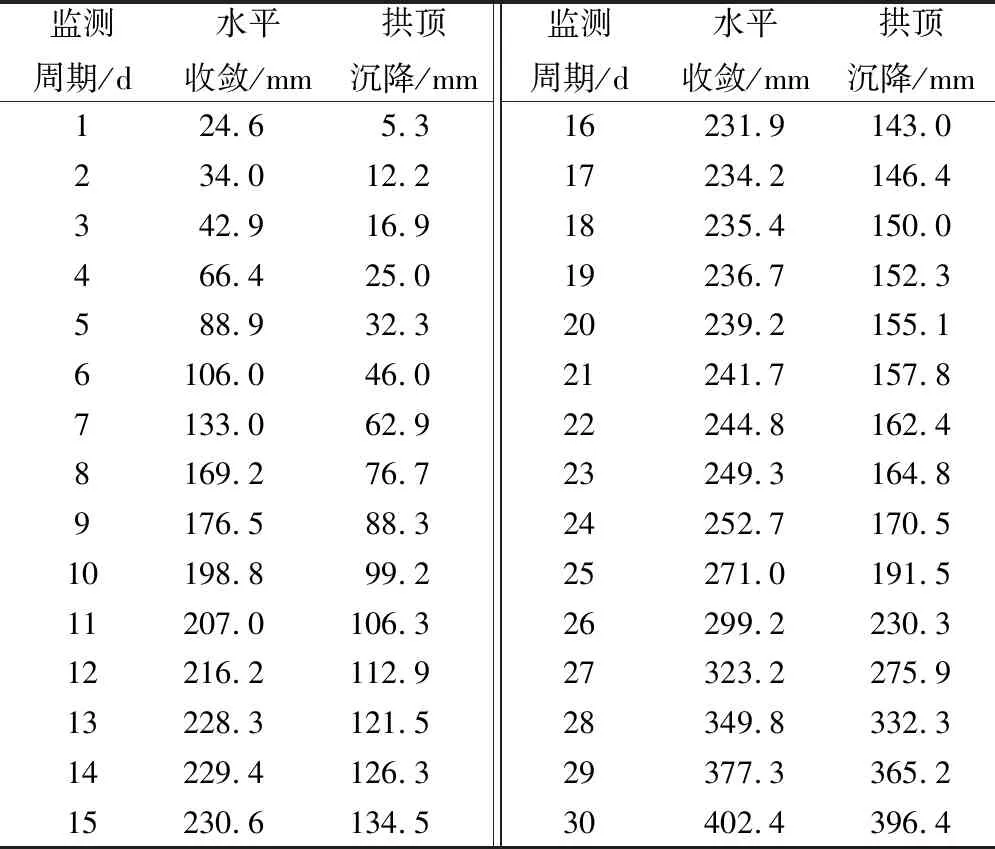
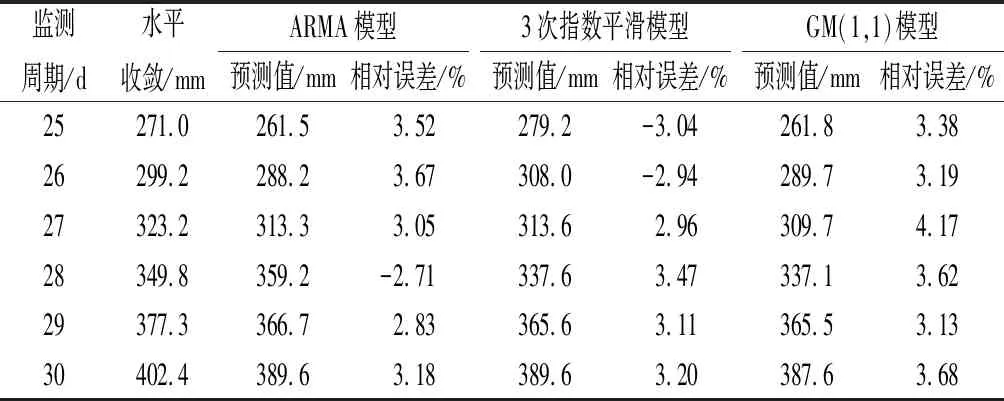
在显著水平a条件下，得到其对应的临界值为Za，进而得到隧道大变形趋势的判据为：当|Z|>Za时，说明检验过程有效；同时，Z为负值时，隧道大变形呈下降趋势，反之隧道大变形呈上升趋势。当|Z|

需要指出的是，当检验水平a值不同时，其对应Za值的显著性判断结果也存在差异，进而可根据不同的检验水平将变形趋势的显著性及等级进行划分，具体如表2所示。

表2 不同检验水平条件下的显著性划分Tab.2 Saliency division under different test levels

2 实例分析

2.1 工程概况

通省隧道隶属十房高速，位于湖北十堰市境内，全长6.9 km，洞轴线间距为48.6 m，纵向走向为235°。根据隧道结构的受力条件，隧道侧墙及仰拱采用圆弧连接，净空采用三心圆曲墙连接。隧址区属中低山地貌，地形起伏较大，高程在565.0～1 223.6 m之间，多呈“V”型沟谷，坡度多在15°～25°之间，坡体植被繁茂，居民及耕地较少。同时，区内岩性较为单一，上覆第四系覆土，以残、崩坡积土为主，下部基岩主要为武当群片岩，多呈全、强风化，中风化基岩埋深较深，且片理化发育，呈片状构造、变晶结构，围岩完整性较差。

隧址区地表水不发育，多以季节性流水为主，少见常年流水；地下水以基岩裂隙水为主，孔隙水次之，其中，基岩裂隙水多赋存于全、强风化带中，而孔隙水多赋存于地表覆土中，两者主要接受降雨补给，季节性影响较大。同时，隧址区位于秦岭-大别山构造带上，使得区内构造发育，进而造成围岩破碎，降低了围岩等级。

在隧道施工过程中，受地质条件的影响，围岩共计发生23次大变形，严重威胁安全施工。如YK110+522断面于5月26日21：00发生大变形，主要变形迹象为局部掉块，进而引发塌方事故，造成断面封堵，围困掌子面施工人员，后经抢险救援，成功救出所有被困人员，所幸未造成人员伤亡。为充分研究此次大变形的变形规律，本文将YK110+515断面的实测数据作为预测分析的数据来源，变形数据如表3所示[17]，可以看出，最大水平收敛量和拱顶沉降量分别为402.4 mm和396.4 mm。

表3 YK110+515断面的实测数据统计Tab.3 Statistics of measured data from YK110+515 section

2.2 变形预测分析

基于前述集成预测思路，对隧道大变形进行预测分析，但限于篇幅，在预测过程中，先详述水平收敛的预测过程，再对拱顶沉降进行综合预测。

2.2.1单项预测分析

在预测过程中，将1～24周期作为训练样本，25～30周期作为验证样本，进而求得3种单项预测模型的预测结果如表4所示。可以看出，各单项预测模型在相应预测节点处的预测精度存在一定差异，验证了各单项预测模型在隧道大变形预测中的差异性，也从侧面说明了进行组合预测的必要性；同时，对3类单项预测模型的相对误差均值进行求解，得出3次指数平滑模型与ARMA模型的相对误差均值相当，分别为3.12%和3.16%，前者预测精度略优，而GM(1,1)模型的相对误差均值为3.53%，与预测精度均略差于前两种预测模型。

表4 水平收敛单项预测结果Tab.4 Single prediction results of horizontal convergence

2.2.2初步组合预测分析

根据预测思路，分别采用线性和非线性组合方法对上述单项预测结果进行初步组合预测。在线性组合过程中，通过误差及方差指标的归一化处理，得到3种单项预测模型的组合系数为：误差权值法=[0.320 0.320 0.361]，方差权值法=[0.154 0.366 0.480]。根据上述组合系数，得到线性组合结果如表5所示。基于表5组合结果，对两种线性组合方法的相对误差均值进行求解，得到方差权值法的相对误差均值为2.45%，误差权值法的相对误差均值为2.36%，与单项预测结果对比可知，线性组合预测在一定程度上提高了预测精度，验证了线性组合预测的有效性。

表5 线性组合预测结果Tab.5 Linear combination forecasting results

同时，也进一步采用BP神经网络和支持向量机对各单项预测模型进行非线性组合，结果如表6所示。类比线性组合方法的分析过程，也对两种非线性组合方法的相对误差均值进行求解，求得BP神经网络组合法的相对误差均值为2.00%，支持向量机组合法的相对误差均值为2.13%。可见，非线性组合预测结果较各单项预测模型也具有相对更高的预测精度，且略优于线性组合的预测精度，进一步验证了组合思路的有效性。

表6 非线性组合预测结果Tab.6 Nonlinear combination forecasting results

2.2.3递进组合预测分析

为进一步提高预测精度及综合利用各初步组合预测结果优势，利用权值贡献系数确定各初步组合预测模型的递进组合权值。通过各初步组合预测模型的评价指标求解，得到各初步组合模型的权值贡献系数如表7所示。

基于表7中权值贡献系数的求解，可实现各初步组合预测结果的递进预测，利用混沌理论进一步优化递进组合预测结果的残差序列，结果如表8所示。

由表8可知，递进组合预测结果的相对误差均值为2.33%，混沌优化预测结果的相对误差均值为1.25%，可见递进组合预测对预测精度的提高不明显，但混沌理论能进一步提高预测精度，验证了集成组合预测的有效性。同时，基于前述预测结果及优化步骤，对31～34周期进行外推预测，可知YK110+515断面的水平收敛将会进一步增加，且增加速率较大，说明该断面的水平收敛变形趋于不稳定方向发展。

表7 各初步组合预测模型的权值贡献系数Tab.7 Weight contribution coefficient of each preliminary combination forecasting model

表8 水平收敛的综合预测结果Tab.8 Comprehensive prediction results of horizontal convergence

2.2.4拱顶沉降预测分析

前述分析验证了集成预测模型在水平收敛中的有效性。为进一步验证该模型的适用性，利用集成预测模型对YK110+515断面的拱顶沉降进行预测分析，得其预测结果如表9所示。

表9 拱顶沉降的综合预测结果Tab.9 Comprehensive prediction results of vault settlement

由表9可知，在相应预测节点处，通过混沌优化预测，均不同程度地提高了预测精度，再次验证了混沌理论的优化效果，且拱顶沉降预测的相对误差均值为1.20%，也进一步验证了集成预测模型的预测精度较高。同时，类比水平收敛的外推预测过程，也对拱顶沉降的31～34周期进行外推预测，得知YK110+515断面的拱顶沉降也将持续增加，趋于不稳定方向发展，与水平收敛的发展趋势一致。

2.3 预测结果的准确性验证

为验证预测结果的准确性，提出利用M-K检验来判断YK110+515断面的变形发展趋势，结果如表10所示。可以看出，水平收敛及拱顶沉降的检验值均大于2.32，即显著性等级为Ⅲ级，呈强显著性上升趋势，说明该断面的变形趋势趋于不稳定方向发展，与前述预测结果相符，验证了集成预测模型在隧道大变形预测中的适用性和有效性。

表10 隧道变形趋势检验结果Tab.10 Test results of tunnel deformation trend

综合上述，集成预测模型的预测结果与M-K检验的变形趋势判断结果一致，相互佐证了各自分析结果的准确性，为隧道大变形防治提供了参考依据。

3 结 论

通过集成预测模型及M-K检验在通省隧道大变形规律研究中的应用，主要得出如下结论。

(1) 组合预测模型可很好地保证预测结果的精度及稳定性，且非线性组合的预测精度略优于线性组合的预测精度；同时，通过混沌优化递进组合预测能进一步提高预测精度，且混沌理论对残差序列的优化效果较好。

(2) 通过集成组合研究，得出隧道大变形呈持续增加趋势，围岩稳定性将进一步变差；同时，M-K检验得出隧道大变形的发展趋势也呈上升趋势，且显著性较强。两者分析结果一致，相互佐证了各自分析结果的准确性，验证了两种方法在隧道大变形规律研究中的适用性。

(3) 隧道大变形受多种因素的影响，单一预测模型难以刻画其变形规律，因此，组合预测模型在隧道大变形预测中的应用价值较高，但鉴于隧址区地质条件的差异性，在组合预测模型的构建过程中，应根据工程实际筛选单项预测模型，并选择合适的组合方法，以保证预测精度。