汽电双驱系统电动机电磁转矩稳定性的研究

闫鑫洋， 徐余法2,， 孙明伦， 彭大华

(1. 上海电机学院 电气学院, 上海 201306； 2. 上海第二工业大学 校长办公室, 上海 201209； 3. 上海电气集团股份有限公司 上海电机厂有限公司, 上海 200240)

在汽电双驱系统中，电机(含电动机和发电机，下同)的运行状态会经常的切换。为了让其运行更加稳定，需要对电机起动、运行、状态变换阶段中转矩的稳定性进行分析和优化。大容量异步电动机在起动、电源电压变化或者负载变化运行工况下，由于电磁暂态的改变引起电动机内部产生冲击电流和瞬时转矩幅值的突变，使得电动机本体受损[1]。文献[2-3]通过优化异步电机的等值电路来推导出电动机的电磁转矩暂态表达式。文献[4]研究了电机在起动过程中的内部特性:电动机在起动和正常运行时都会伴随着大量的谐波损耗，在接通正弦三相交流电后，由于电动机的气隙磁势在空间并非正弦分布，而是有限数目的阶梯状波形，会产生一系列的谐波磁通[5-7]。这些谐波磁通会产生附加损耗，使内部温度升高，影响电动机的寿命。同时，这些谐波磁通会产生附加转矩，影响电动机的起动和运行，产生电磁转矩的脉动[8-10]。文献[11]分析了谐波对电动机电磁转矩的影响，但没有定量地分析出它们之间的关系。文献[12]列出了常见的汽轮发电机电磁转矩的分析计算方法和理论依据。本文以电磁理论为基础，分析异步电动机在起动过程中电磁转矩振荡原因。运用虚位移法和麦克斯韦应力法，对各类谐波转矩产生的机理进行分析。结合Ansys和Matlab软件计算出异步电动机谐波震荡转矩数值，通过计算结果得出电机优化方案。

1 起动阶段的转矩脉动

异步电动机在起动时，由于定子产生的旋转磁场转速远大于转子转速。从定转子绕组特性分析，可将其视为感性负载。因此，电动机状态不会呈线性变化，定转子绕组中将会含有稳定的交流电分量和暂态的衰减直流电分量。

1.1 磁场与能量

由电机学原理可知，定转子电感储存的能量和定转子之间互感储存的能量组成了电机的磁场总能，有

(1)

式中：θme为转子的电位置角；θm表示转子的空间位置角；Lss为电机定子自感；Lrr为转子自感；Lsr为定转子互感；p为极数；is为定子电流；ir为转子电流。

电磁转矩Tem为磁场总能量Wm对空间位置角θm的导数，即

(2)

由式(1)和式(2)可知，电动机在起动阶段的电磁转矩是由电动机的定转子电流中的稳态交流分量和暂态衰减直流分量相互作用所产生的电磁转矩:① 稳定的转矩分量。② 定转子电流中的稳定交流部分与衰减较慢的直流部分相互作用产生的转矩。这种转矩会持续比较长时间，对电机稳定所需时间影响最大。③ 定转子电流中的稳定交流部分与衰减较快的直流部分相互作用产生的转矩。这种转矩对电机的震荡初始幅值影响最大，但持续时间较短。④ 由定转子电流中衰减直流电流部分相互作用产生的转矩。

因此，当电机加载三相对称电压，并且定转子初始电流均为0时的电机瞬态电磁转矩为

Tst=Tst(稳态){(1+e- α2te- α3t)-

(e- α2t+e- α3t)cosω1t-

(e- α2t-e- α3t)sinω1t}

(3)

式中：Tst(稳态)为稳态时电动机的起动转矩；α2为主磁场衰减系数；α3为漏磁场衰减系数。

可见，电动机在起动过程中，电磁转矩中包含多种分量，并且以震荡的形式逐步衰减。

1.2 转子运动方向

根据异步电动机的机械平衡方程，有

(4)

式中:Tm为负载转矩；TΩ为摩擦转矩；J为电机的转动惯量。

由此可知异步电动机的转矩与电机的转动惯量、电磁转矩、负载转矩、摩擦转矩有关。电机的电磁转矩受到电机内部电参数(电机极对数、定转子电阻电抗、转动惯量等)和电机外部参数(加载在电机端部的电压幅值与频率)的影响。

1.3 利用Ansoft软件仿真验证

根据电机模型的参数(见表1)利用Ansoft软件对电机进行建模仿真。所建模型如图1所示。

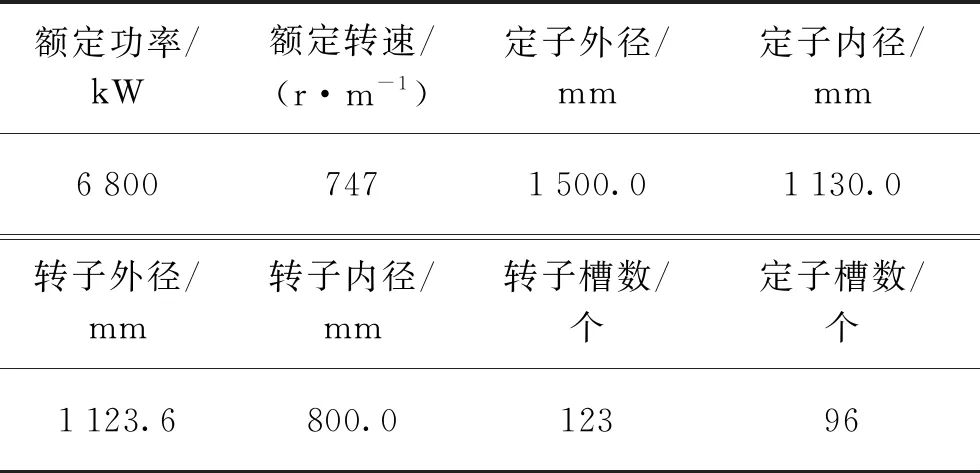
表1 电机相关尺寸及参数

图1 电机有限元剖分模型(电脑仿真截图，单位：mm)

用式(1)和式(4)，对电动机在空载工况和风机负载工况下进行起动和运行状态的仿真。利用参数化设计，改变加载在电动机上的端电压U、电压频率f、定子电阻Rs、定子电感Ls和转动惯量J。通过实验系统、全面仿真分析出这些电参数对电动机起动、运行阶段电磁转矩和频率的影响。

经过大量仿真数据的收集整理比较，得出电动机在空载状态下电磁转矩震荡与电动机电参数之间的关系(见表2)。

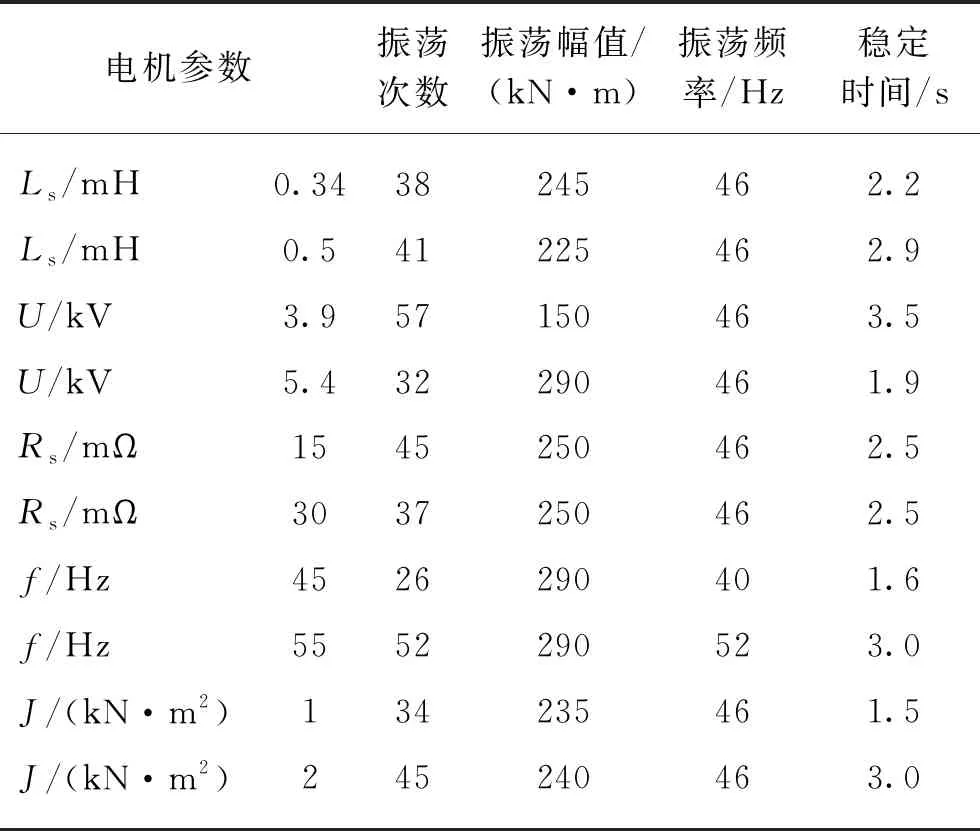
表2 电动机空载状态下电磁转矩震荡统计

“汽电双驱”系统中，当电机从电动机状态转化为发电机状态时电机电磁转矩震荡与电机参数之间的关系见表3。

表3 发电状态时电磁转矩震荡统计表

1.4 仿真结论分析

从实验数据可知，改变电机的端电压、端电压频率、电机参数对电机的电磁转矩振荡幅值和振荡次数都有影响。

(1) 由实验和公式推导可得改变加载端电压的大小，转矩振荡幅值成平方关系变化。当加载的电压幅值越大，电磁转矩振荡的次数越少，电机达到运行稳定所需要的时间越短，而电磁转矩振荡幅值相应的也就越高。

(2) 通过比较发现，所有的影响因素中，唯一对电磁转矩振荡频率有影响的参数是加载电压的频率，频率越高电机转矩振荡的频率也随之变高，且振荡频率小于或等于加载电压频率。

(3) 电阻和电感的适当增加可以减少振荡的次数和减少电磁转矩振荡过程需要的时间。影响电磁转矩振荡时长的主要因素是电机的转动惯量J和加载电压的频率大小。增大转动惯量将使电磁转矩振荡时长加大，也相应的增加了电磁转矩的振荡的次数。

2 稳定运行阶段的转矩脉动

2.1 转矩脉动理论分析

由电机学原理可知:电机的气隙中存在着除基波磁场外大量的谐波磁场，这些磁场之间相互作用会产生附加转矩。附加转矩降低了电机运行的稳定性，增大了电机的损耗，也加剧了电机的振动与噪声。

在电机的谐波电流中，对转矩波动影响较大的是谐波电流与基波磁场相互作用产生的谐波转矩和阶数较高的齿谐波产生的附加转矩。并且谐波的幅值会随着谐波次数的升高而降低。根据虚位移法得附加转矩为

(5)

式中：p为电机的极对数；θ为两相互作用磁场的虚位移；Wm为气隙磁场储能。

基波磁场在气隙中的磁密分布可以理解为标准的余弦分布，有

b1=B1cosθ

(6)

则k次谐波磁密分布表达式为

bk=Bkcos(θ+θ1k)

(7)

式中：B1为基波磁场幅值；Bk为k次谐波幅值；θ1k为基波与k次谐波间夹角。

由电磁场理论，有

(8)

式中：μ0=4π×10-7H/m，为气隙的磁导系数；D为电机定子内圆直径；g为气隙有效长度；l为电机轴向有效长度；b为合成磁场，b=b1+bk。

将式(6)～式(8)代入式(5)中得到基波磁场与k次谐波磁场相互作用后产生的脉动谐波转矩为

(9)

因而电机所受到的脉动谐波转矩可理解为基波磁场与各阶谐波产生的脉动谐波转矩之和

Te=∑Te1k，k=5,7,…

(10)

由此可得，电机的电磁转矩是由电机在不同状态下由不同频率、不同振幅的谐波电流和谐波磁通共同作用产生的。

2.2 有限元验证分析

对电机在稳定状态下的电磁转矩进行分析。通过Maxwell软件进行建模仿真，得到其在风机负载情况下的气隙磁密如图2所示。

图2 异步电动机的磁密分布图

利用Ansoft软件的场计算器，对电动机的径向气隙磁密和切向气隙磁密计算求解，并对得到的结果进行傅里叶变换，分解出径向和切向气隙磁密的谐波构成和幅值。

经过分析，电动机运行时第23、第25次齿槽谐波数值高于其他次谐波。第5、第7、第11、第13次谐波气隙磁密的数值也较高。将径向和切向两个方向的气隙磁密合成，计算出电动机的各次谐波所产生的的气隙磁密如表4和表5所示。

结合表4和式(5)～式(10)，计算出电动机中的各次脉动谐波转矩(见表5)。

表4 电机谐波磁密幅值

表5 电机谐波转矩幅值

由表5可知，电动机的脉动转矩中含有的23次和25次谐波转矩远大于其他频率的谐波转矩。可以得出电动机的转矩脉动中，齿谐波转矩脉动对电动机的影响值远大于电动机其他因素产生的谐波转矩脉动。23次齿谐波转矩为额定转矩的5.4%，25次齿谐波转矩为额定转矩的3%。齿谐波的合成因素对电动机的运行、驱动性能会有很大的影响。

3 结 论

本文对汽电双驱系统中电机状态进行建模仿真。对电动机在起动状态和稳定运行状态时电磁转矩的稳定性进行整理分析。

(1) 对电动机的起动阶段进行理论推导和分析。电动机起动时转矩振荡的原因和影响其振荡的因素是电动机的电参数和加载在电动机上的电源特性共同影响产生的结果，单从改变电参数着手以减小电动机的转矩振荡效果非常有限，必须要增加电动机控制系统才能大幅改善相关特性。

(2) 通过数据的参数化设计，仿真分析不同参数对电动机起动时转矩振荡的影响。仿真数据证明了电动机起动阶段转矩振荡理论推导的正确性。因此，从电动机的参数出发，在不影响性能的情况下对电动机起动过程中转矩振荡的幅值、频率和持续时间问题进行优化：通过适当的增加电动机的漏抗来抑制电流中的高次谐波从而降低电动机的附加转矩。

(3) 从仿真波形中分析电动机稳定状态下的转矩脉动问题。通过Ansoft软件的分析、Matlab软件对仿真数据的处理，运用虚位移法和麦克斯韦应力法对电动机转矩分析计算，求解出电动机运行稳定状态下各次谐波脉动转矩的大小，得出对此电动机影响最大的是第23、第25次齿谐波转矩脉动。这些齿谐波产生的附加转矩，使得电动机出现转矩振荡，对起动影响较大。

相关结论对进一步研究谐波转矩对汽电双驱系统的影响是有益的，后续可进行深入研究。