思维可视化技术体现逻辑推理

李青

摘 要：文章借助思维可视化技术分析证明立体几何中的垂直问题，将复杂的逻辑推理问题层层解析，感受思维可视化技术的优势，并在这一过程中注重逻辑推理这一核心素养的培养.

关键词：思维可视化;数学学科;核心素养;培育路径

核心素养之一的“逻辑推理”，是指從一些事实和命题出发，依据逻辑规则推出一个命题的思维过程，主要包括两类推理，一类是合情推理，包括归纳推理和类比推理，另一类是演绎推理。数学公式、定理、性质等结论的教学是新授课的主要内容，对于某些重点、难点结论的发现和证明，既符合新课标倡导的“让学生体验数学发现和创造的历程”，也是培养学生逻辑推理能力的好素材。逻辑推理主要包括合情推理与演绎推理两种推理形式，对于逻辑推理核心素养的生成关键在于培养学生清晰的、有条理的、合乎逻辑的理性思维品质。因此，可以借助高中数学中的代数证明与几何证明来培养学生的演绎推理。

《新课标》强调，教师应当摒弃以枯燥授课与大量练习为主的教学模式，注重培养学生的数学思维与核心素养.逻辑推理作为高中数学六大核心素养之一，是学生得到数学结论、构建数学知识体系的重要方式。在本文中，笔者根据多年的教学实践，以一道立体几何的证明题为例，在思维可视化技术中呈现逻辑推理，简单探讨培养学生逻辑推理能力的具体策略，旨在发展学生的数学核心素养。

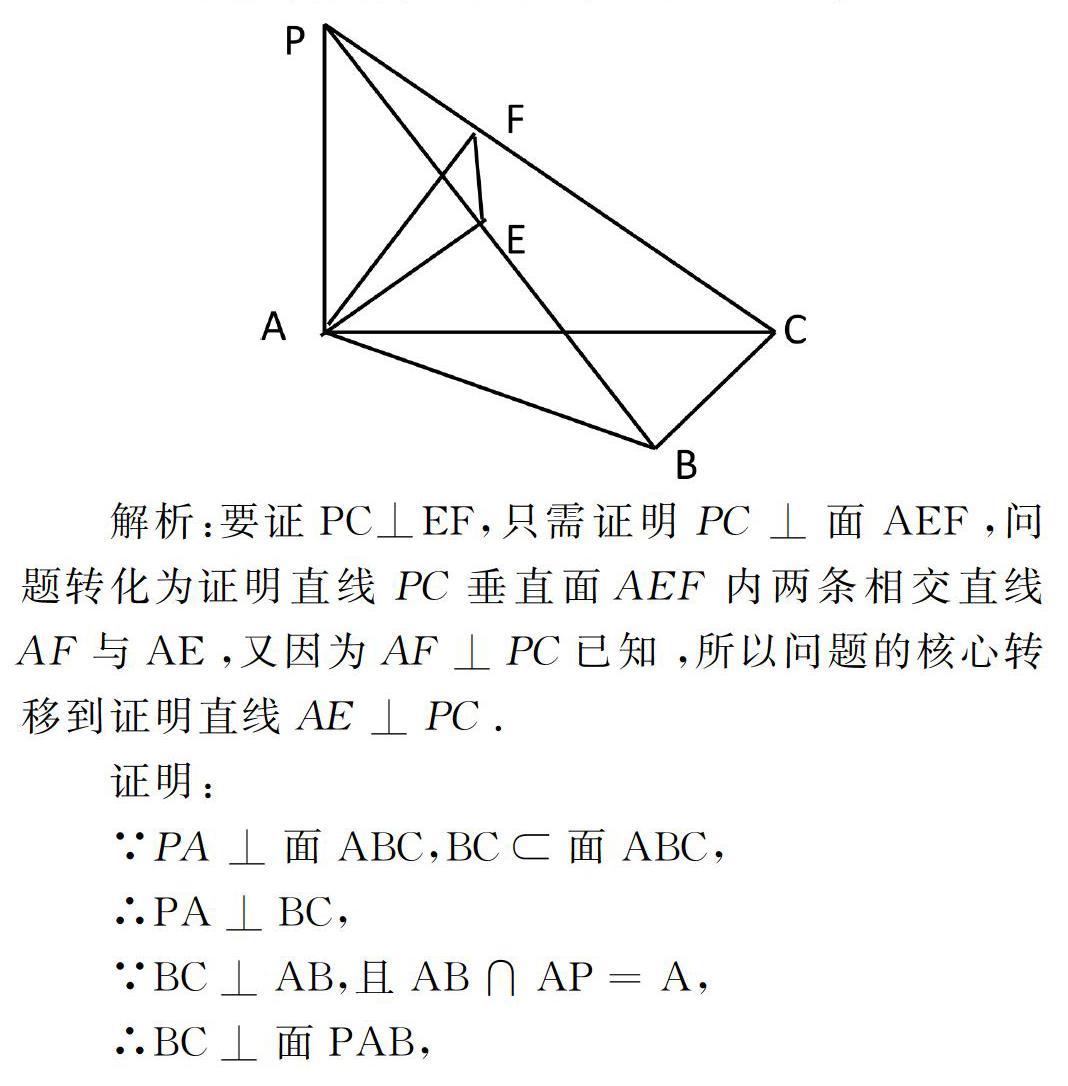
案例：如图，PA⊥平面ABC，AE⊥PB，AB⊥BC，AF⊥PC，垂足分别为E、B、F求证：PC⊥EF;

由于此题的逻辑性较强，学生理解难度大，为便于学生理清解题思路，可借助思维导图呈现逻辑推理过程如下：

本图的优点在于能弱化学生的理解难度，将笼统的逻辑推理问题分步呈现，清楚每一步已有结论和待证明结论，让学生的思维层层细化，顺藤摸瓜，最终将每一步待证明结论回归已知条件或公理、定理，进而问题得以解决。

在日常的教学活动中，广大教师想必同笔者一样，总是会遇到这样一些情况： 平时对学生反复讲解的一类问题，在考试中遇到同样的问题时学生还是不知所措; 对旧问题稍加改编，学生就变得一头雾水，经常是老师一讲就会，学生一做就错……出现这些问题的原因正是因为学生仅仅停留在了模仿照抄、机械学习的层面上，而缺少新认知与已有认知间的联系.基于这一点考虑，我们借助思维可视化技术让学生真正感悟数学的真谛，领会思维的过程，找到解决问题的路径和方法，建立已知和未知知识间的联系，最终达到有意义学习的目的.

参考文献

[1]张艳.基于逻辑推理数学核心素养培养模式的尝试——以“对棱相等四面体的由来”为例[J].中学教研（ 数学），2018.

[2]明永学.培养逻辑推理能力 发展数学核心素养[J].高中数学教与学，2018.