掘支锚联合机组支撑油缸多目标优化设计

谢 苗 李晓婧

辽宁工程技术大学机械工程学院，阜新，123000

0 引言

随着我国煤矿开采强度的不断增加，巷道综合机械化快速掘进技术逐渐成为提高综掘工作效率的必由之路[1-2]。但目前综掘工作面还采用分段作业方式进行，工序复杂、掘进效率低[3]。在此背景下，笔者从提高工作效率与安全生产的要求出发，研发了集掘进与支护、锚固为一体的掘支锚联合机组(以下简称：联合机组)。联合机组的支护机构与顶板接触，顶板的压力直接作用在支护机构上，所以支护机构结构参数是关键影响因素之一。本文采用Workbench软件分析联合机组支护机构的结构参数对其最大应力与最大位移的影响，然后在满足支护机构给定约束条件的前提下，对其进行多目标优化设计[4-6]，得到支护机构的最优结构；最后利用试验样机检测方法，证明优化设计的有效性。

1 联合机组

联合机组是集掘进、临时支护、锚固功能为一体的综掘装备，如图1所示，工作面呈现机械化状态，大大减小了工人的劳动强度，提高掘进效率。支护机构采用拱形顶梁两组交替支撑方式，每个顶梁上安装多个支撑油缸，以此适应顶板形状，并在掘进工作时支护巷道，防止顶板垮落，使掘进工作更加安全。此外，在掘进间歇可带动掘进机构向前迈步推移，省去了传统掘进机的行走机构，使整机结构简单，质量减小。

图1 掘支锚联合机组Fig.1 Excavation and anchor combined unit

2 顶板与支护机构支撑油缸作用关系

支护机构支撑油缸作为联合机组与顶板直接接触的结构，由于顶板不规则性[7]，支撑油缸在支撑顶板过程中，不仅可以起到储存并释放能量的作用，还可以吸收顶板的轻微振动和冲击，起到减缓剧烈振动的作用，因此从支撑油缸的功能上来看其作用等效于弹簧系统。考虑到支撑油缸上述重要作用，当支撑油缸无法正常工作时，顶板压力直接作用到支架顶梁，造成顶梁压力过大，导致整个设备发生重大故障，引起不可预测的意外事故。因此，在支撑油缸的设计阶段就要对其支撑强度进行参数设计，以实现支撑油缸的最优设计。

3 联合机组支护机构多目标优化设计

3.1 模态分析

联合机组单组支护的三维模型采用SolidWorks建立，并导入Workbench以便有限元分析，如图2a所示。由于支撑油缸内部存在高压油液且油缸本身结构比较复杂，所以建立支撑油缸模型时对其结构适当简化，并将内部油液产生的支撑刚度用等效弹簧替代，如图2b所示，根据支撑油缸工作压力确定弹簧刚度为108N/m。

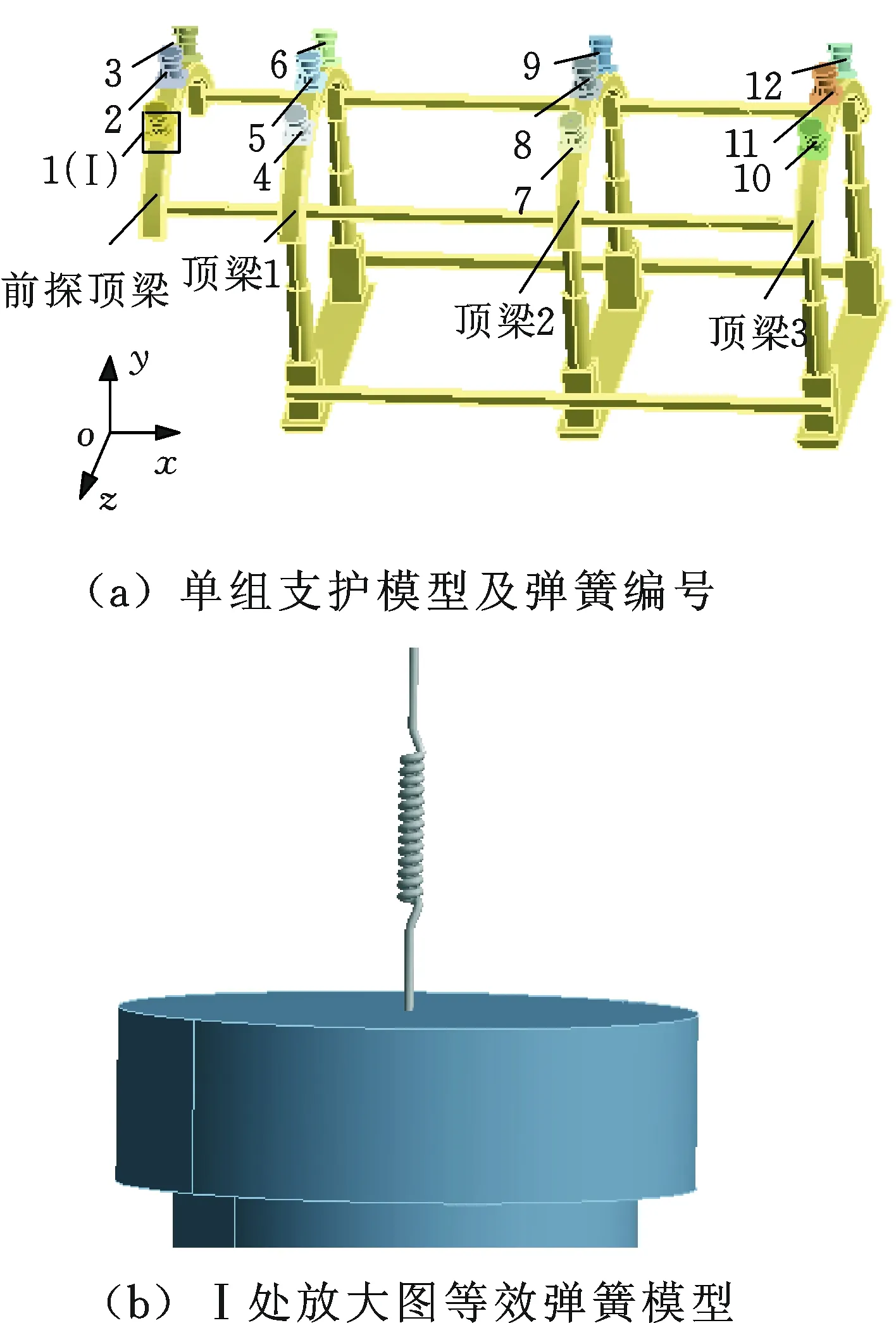
图2 联合机组支护机构的三维模型Fig.2 Three-dimensional model of combined unit support mechanism

支护机构材料选用45钢，密度为7 850 kg/m3，弹性模量为200 GPa，泊松比为0.3，屈服极限为235 MPa，剪切模量为80 GPa。采用六面体和四面体混合划分网格，分别包含316 524个节点和181 418个单元体，如图3所示。

图3 网格模型Fig.3 Mesh model

联合机组单组支撑部分执行支撑任务时，底座直接与底板接触，无相对位移，处于受约束状态，因此，对主支撑支护机构底座添加完全约束，设置分析模型的前6阶固有频率和振型，计算结果如图4所示。

由图4可知结构的1阶频率为35.571 Hz，振型为前探顶梁绕X轴扭振；2阶频率为43.226 Hz，振型为所有顶梁沿X轴摆振；3阶频率为63.885 Hz，振型为前探顶梁沿X轴摆振；4阶频率为98.615 Hz，振型为所有顶梁沿X轴左右交替性摆振；5阶频率为113.66 Hz，振型为顶梁1和顶梁3沿X轴摆振；6阶频率为123.37 Hz，振型为所有顶梁沿X轴摆振。

图4 模态振型Fig.4 Modal shape

3.2 谐响应分析

为进一步研究联合机组支护机构在激振力作用下的响应情况，需对其进行谐响应分析。由结构的工作状态可知顶板的作用力直接作用到各支撑油缸上，根据文献[8]可知总的作用力F=10 kN，假设每个支撑油缸的受力大小相等，即在每个支撑油缸与顶板接触面上施加833 N的激振力，激振力的方向与油缸的轴向相同，激振力的相位为零，施加的激振力如图5所示。根据模态分析的结果可知结构的前6阶固有频率范围为35.571～123.37 Hz，因此设置分析的频率f范围为20～150 Hz，设置求解计算的步长为2.5 Hz。分析时对模型施加的约束条件与模态分析时相同。

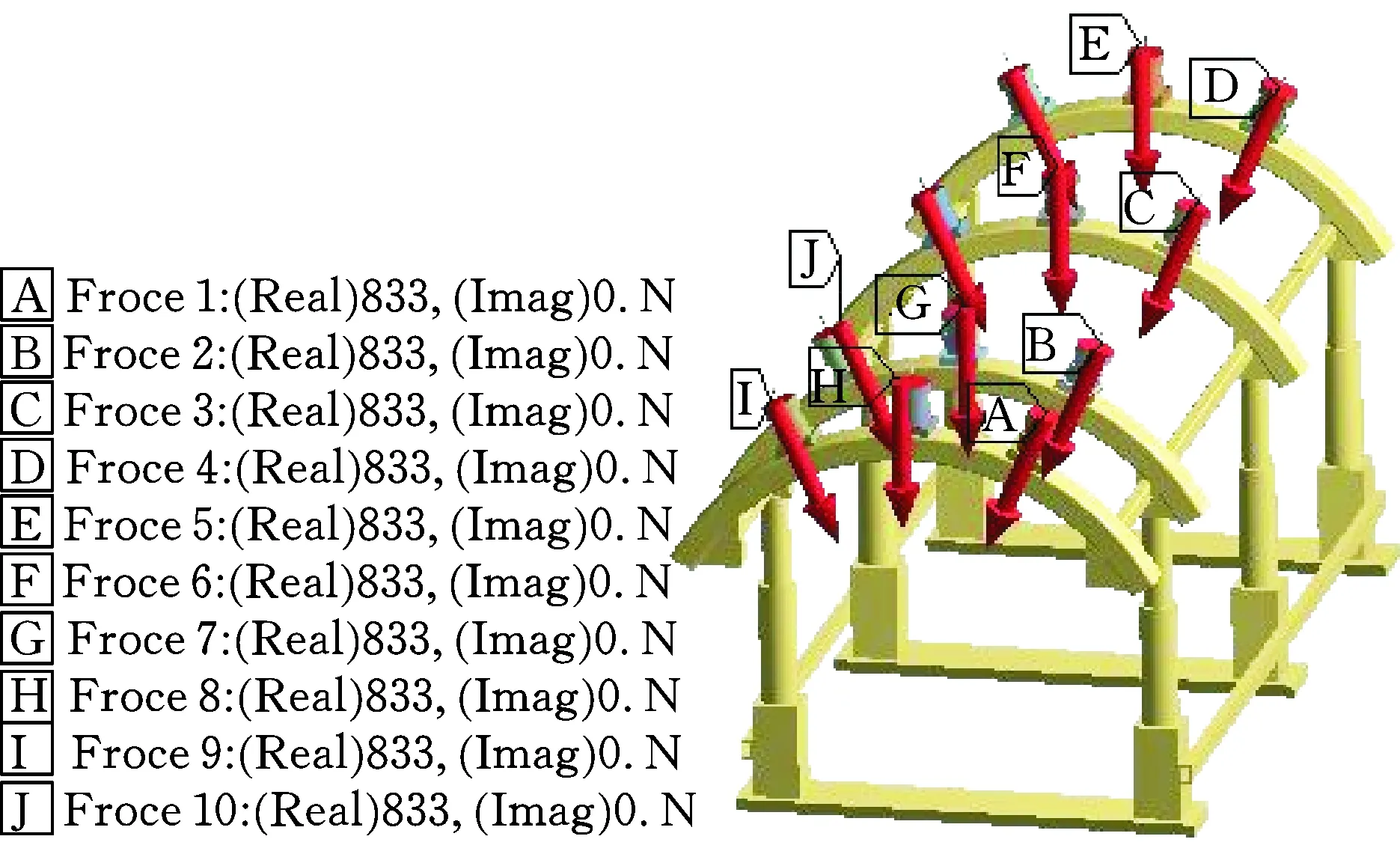
图5 单组支撑激振力模型Fig.5 Single group support excitation force model

模型的应力响应曲线如图6所示。由图可知，当激振频率为65 Hz左右时(该频率为模型的第3阶频率)，模型在X、Y、Z3个坐标方向上最大应力σ1分别为35.893 MPa、14.044 MPa、10.637 MPa；同时当激振频率为115 Hz左右时模型也存在较大的应力，模型在X轴方向的应力响应最大，该方向是主要响应方向。

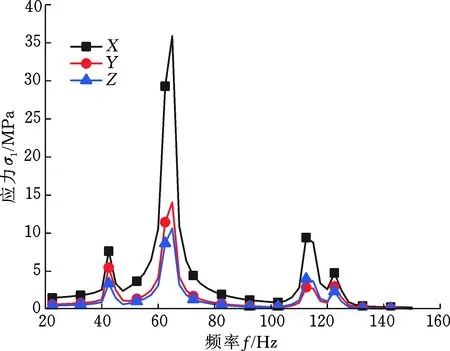
图6 应力响应曲线Fig.6 Stress response curve

模型的位移响应曲线如图7所示。由图可知，当激振频率为65 Hz左右时(该频率为模型的第3阶频率)，模型在X、Y、Z3个坐标方向上最大位移振幅r1分别为223.71 μm、42.224 μm、13.397 μm；同时当激振频率为115 Hz和125 Hz时模型也存在较大的振幅。根据图5可知模型在X轴方向的位移响应最大，该方向是主要变形方向。

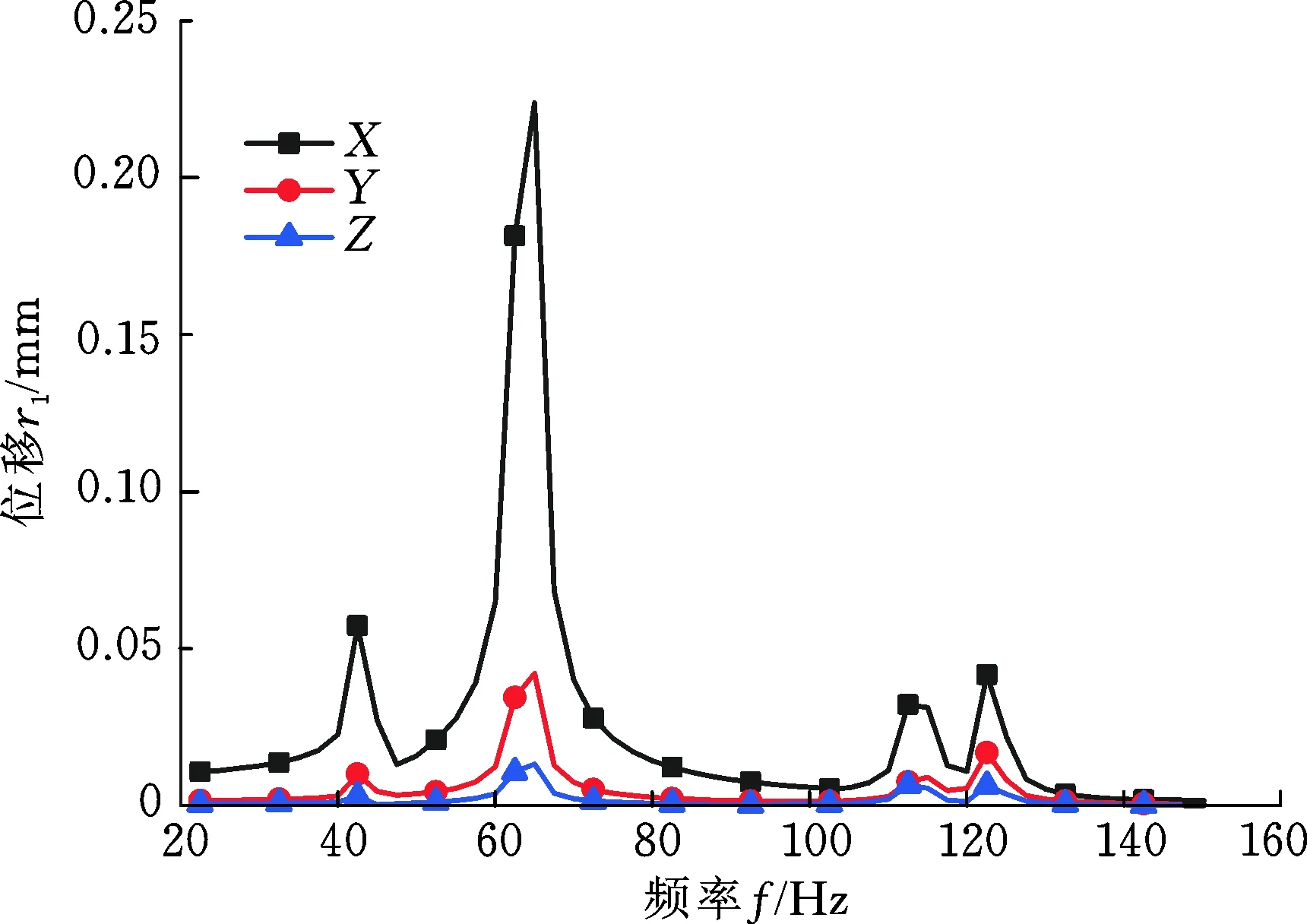
图7 位移响应曲线Fig.7 Displacement response curve

3.3 弹簧刚度对支护机构的动态性能响应曲面分析

根据第2节分析，支撑油缸的弹簧刚度对结构整体的动态性能及安全性有显著影响，本节采用灵敏度分析的方式研究它们之间的变化规律。

在Workbench软件中将各弹簧刚度设为输入参数，因整个模型有12个油缸即该模型共有12个输入参数P=[P1P2…P12]T，各弹簧代号如图2a所示，根据实际工况[9]将各弹簧刚度k的研究范围设为107～109N/m。为寻求最优的弹簧刚度使模型在3个坐标轴方向的位移响应幅值及应力响应幅值最小，将模型在3个坐标轴方向的位移响应幅值及应力响应幅值设为输出函数。

采用响应曲面法研究各个输入参数对输出参数的影响。由图6和图7可知模型在X轴向的应力和位移显著高于其余2个方向，因此只列出了各个弹簧刚度对X轴向的应力和位移的影响，如图8和图9所示。由图可知，设计参数P1和P3对模型的位移r2和应力σ2有较大影响，其余参

图8 弹簧刚度对应力振幅的影响Fig.8 Effect of spring stiffness on stress

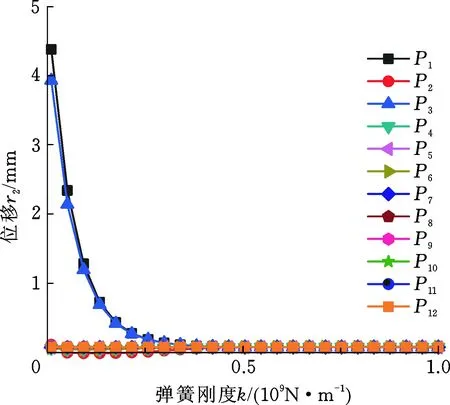
图9 弹簧刚度对位移的影响Fig.9 Effect of spring stiffness on displacement

数影响较小。P1和P3在交互作用下对模型位移的影响如图10所示，由图10可知模型的位移随着两个变量的增大而迅速减小，当P1=1.66×108N/m、P3=1.87×108N/m且其余参数为108N/m时有最小位移4.2 μm。P1和P3在交互作用下对模型应力的影响规律与其对位移的影响规律相同。

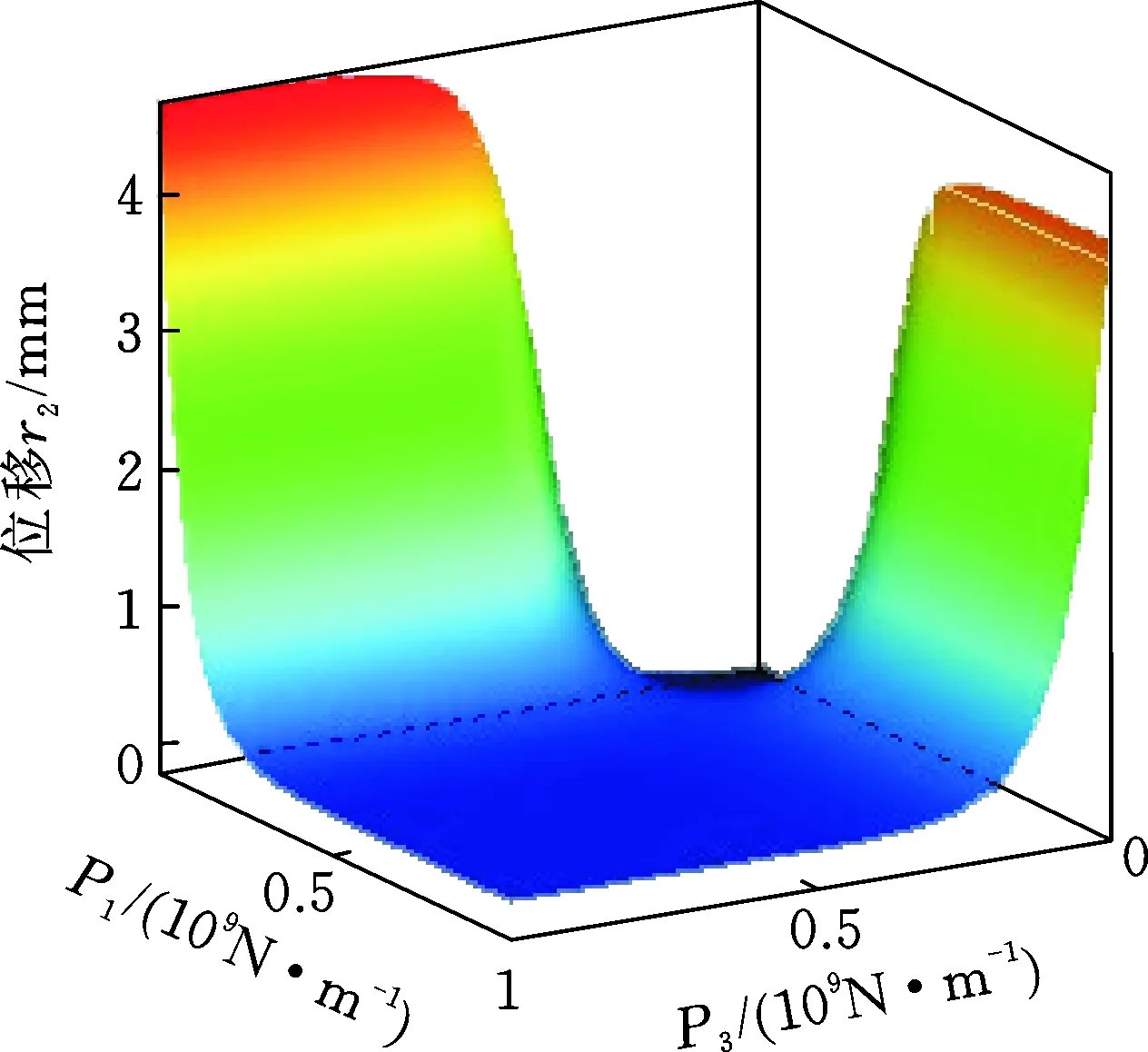
图10 P1和P3对位移振幅的影响Fig.10 Effect of P1 and P3 on displacement

本节既确定了影响较大的设计参数，也确定了各个输入参数对输出参数的影响规律。在后文的优化设计中，确定最终优化结果时要根据各输入参数对输出参数的影响规律适当圆整。

3.4 优化设计

根据3.3节分析可知，各设计参数并未在初始设计点附近取得最优，同时考虑到各影响相对较小的设计变量之间的交互作用可能对各输出变量产生较大的影响，所以为了能够全面考虑各设计参数的影响，将模型中12个弹簧刚度作为设计变量，并以模型谐响应的最大位移最小和最大应力最小为优化目标函数，进行优化设计。优化时，各弹簧刚度与前文响应曲面分析时相同，因此优化设计的数学模型为

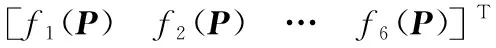
(1)

s.t.P=[P1P2…P12]T

107N/m≤Pi≤109N/m

i=1,2,…,12

式中，f1(P)～f3(P)为模型在3个轴向的位移响应；f4(P)～f6(P)为模型在3个轴向的应力响应;Pi为各弹簧刚度。

利用Workbench软件中Direct Optimization模块进行优化，并设置求解方法为自适应多目标优化方法。对于联合机组支护机构的安全性尤为重要，所以设置各应力目标函数的重要性为higher，其余目标函数的重要性设为默认。优化后的各弹簧刚度如表1所示。

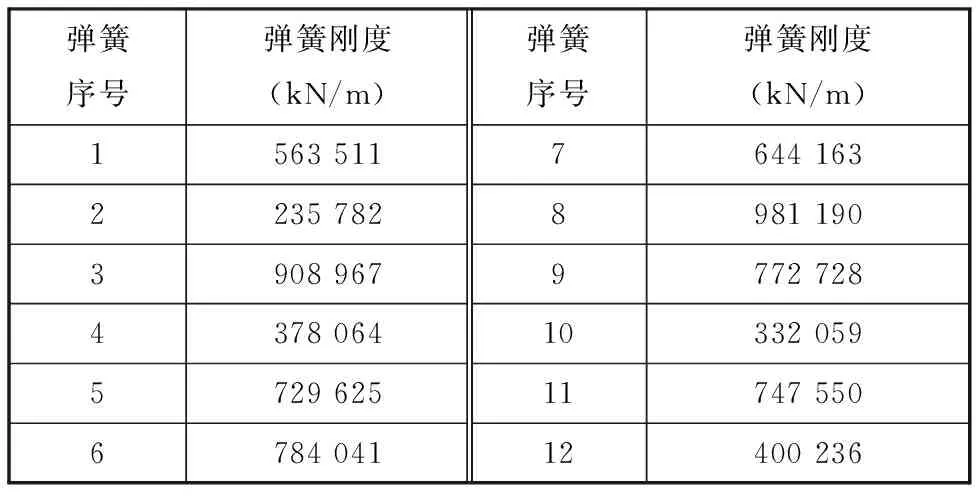
表1 弹簧刚度

优化后模型的应力响应σ3和位移响应r3如图11和图12所示，其中优化后模型在3个轴向的最大应力响应分别为1.176 MPa、0.580 2 MPa、0.356 MPa，与优化前相比分别减小了96.72%、95.87%、96.65%；优化后模型在3个轴向的最大位移响应为4.1 μm、10.72 μm、14.55 μm，优化后的模型在Z轴方向的最大位移响应虽然比优化前略有增大，但在X和Y轴方向的最大位移响应分别减小了98.17%和74.61%。

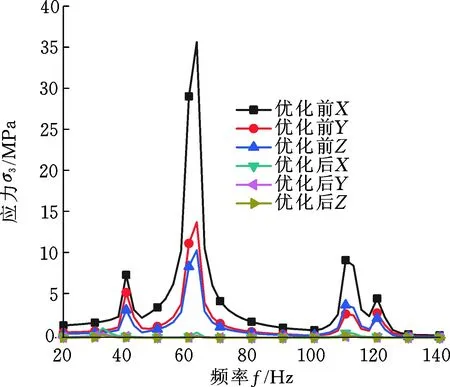
图11 应力响应对比Fig.11 Comparison of stress responses

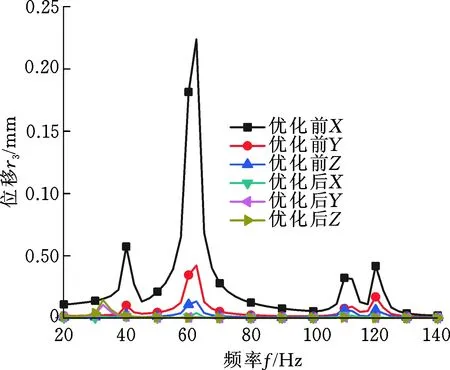
图12 位移响应对比Fig.12 Comparison of displacement responses

4 联合机组支护机构动态性能检测

为了验证优化的有效性，研制掘支锚联合机组并采用东华动态检测系统检测样机的动态特性。研制的样机如图13所示。动态检测系统主要包括动态测试仪和加速度传感器等构成。实验时采用力锤敲击产生激励信号，加速度传感器拾取响应信号，动态测试仪处理输入信号和输出信号并求得结构的动态特性。

图13 联合机组试验台Fig.13 Combined unit test bench

优化设计使结构在X轴向的动态特性得到了显著改善，所以实验检测结构在X轴向的频响特性，结果如图14所示。由图确定模型的前6阶固有频率如表2所示，其中实验测得模型前6阶固有频率与仿真结果的最大误差为8.6%，最小误差为2.31%。实验所得的频响曲线与仿真所得的频响曲线变化规律基本一致，证明了优化设计的有效性。

图14 结构在X轴向的频响曲线Fig.14 Frequency response curve of structure in X axis

阶数实验频率(Hz)仿真频率(Hz)相对误差(%)132.74835.828-8.6240.73543.297-5.92367.89164.4695.31496.64598.926-2.315117.252113.693.136126.198123.412.26

5 结论

(1)优化前模型的固有频率为35.571～123.37 Hz，模型在X、Y、Z3个方向上最大应力幅分别为35.893 MPa、14.044 MPa、10.637 MPa；模型在X、Y、Z3个方向上最大位移振幅分别为223.71 μm、42.224 μm、13.397 μm。

(2)采用参数化建模和参数化分析方法分析了各弹簧刚度对结构的位移和应力的影响，确定了参数P1和P3是关键影响因素。

(3)优化后模型在3个轴向的最大应力响应分别为1.176 MPa、0.580 2 MPa、0.356 MPa，比优化前分别减小了96.72%、95.87%、96.65%；优化后模型在3个轴向的最大位移响应为4.1 μm、10.72 μm、14.55 μm，优化后的模型在Z轴方向的最大位移响应虽然比优化前略有增大，但在X和Y轴方向的最大位移响应分别减小了98.17%和74.61%。