改进的正弦混沌系统及性能分析∗

高晓芸 吴成茂 田小平

（西安邮电大学电子工程学院 西安 710121）

1 引言

混沌行为广泛存在于许多自然和非自然现象中，如香烟燃烧的运动，海水的潮汐运动，天气和气候［1］等，混沌理论科学研究促进了人们对自然的认识。混沌是一种非线性现象，是确定性非线性系统产生的类似随机性的行为，确定但又难以预测［2］。混沌是指在非线性动力系统中出现的确定性、类似随机的过程，这种过程既非周期又非收敛，并且对初值具有极其敏感的依赖性［3～6］。正是因为这些重要的性质，混沌理论被广泛应用在不同的科学和工程领域［7～9］，尤其在密码学和通信［10～12］领域。混沌系统的遍历性、伪随机性、有界性、对初始值高度敏感性，使混沌系统生成的伪随机序列很适合于信息加密，具有良好的扩散和混乱效果。因此，如何产生一种具有优良混沌性能的混沌系统显得尤为重要。

近年来也不断有新的混沌系统被提出，其中文献［13］提出了一种利用已有的混沌映射获取新混沌映射的轮切换系统，但生成的新混沌映射的混沌性能有限，不具有鲁棒性［14］。文献［15］引入了一个参数控制混沌系统来生成新的混沌映射，生成的混沌映射一些具有良好的鲁棒性，而有的则混沌性能较差，不具稳定性［16］。文献［17］提出了一个新的一维混沌系统，可以生成具有鲁棒性的新混沌映射，但是由于包含模块化操作，故新混沌映射的性能可能无法在理论上进行分析［18］。

针对基于正弦变换的混沌系统（sine-transform-based chaotic system，STBCS）构 造 出 来 的Tent-Sine混沌映射的鲁棒性、复杂性和不可预测性低等不足，文章提出了Tent-Sine混沌的延时混沌映射。首先是对Tent-Sine混沌映射执行延时一到八个单位的延时操作，再通过Matlab仿真，对各个延时Tent-Sine混沌映射的分叉图、样本熵、Kolmogorov熵测试与分析，实验结果表明了该方法的有效性。

2 传统的混沌系统

Sine映射、Tent映射是两种常见的经典混沌系统，它们将被用作种子映射来生成新的混沌映射。

Sine混沌映射是由正弦函数派生出来的正弦映射，它是将[0，1/π]范围内的输入角度转换到一定范围内输出。正弦映射的数学模型定义如下：

其中xi是输入，xi+1是输出，S(xi)表示Sine映射，r是控制参数。其分叉图如图1（a）所示。

Tent映射根据其范围拉伸或折叠输入变量，若输入小于0.5，则延长输入；否则折叠输入。Tent映射定义如下：

其中xi是输入，xi+1是输出，T(xi)表示Tent映射，r是控制参数。其分叉图如图1（b）所示。

分叉现象是指动力系统的定性行为随着参数的改变而发生质的变化，用于描述动力系统的输出范围随其参数的变化情况。

3 正弦变换混沌映射系统

3.1 正弦变换混沌系统的构造方法

正弦变换混沌系统构造的原理示意图如图2所示。

图2 正弦变换混沌系统构造原理图

其中 f(a，xi)和 g(b，xi)分别是具有控制参数a和b的两个种子映射，该组合是两个经典种子混沌映射线性加权的输出，而正弦变换对组合的结果执行非线性变换。在每次迭代的过程中，输入xi被同时反馈到 f(a，xi)和 g(b，xi)中，然后对f(a，xi)和g(b，xi)的组合输出进行正弦变换。

设N(xi)表示STBCS，其定义如下：

任何现有一维混沌映射都可用作STBCS的种子映射。用户可将种子映射 f(a，xi)和g(b，xi)设置为相同或不同的混沌映射。

1）当 f(a，xi)和 g(b，xi)是相同的一维混沌映射时，STBCS可表示为

或

在这种情况下，两个不同控制参数混沌映射的输出线性组合，而并非线性变换以获得更复杂的混沌行为，故STBCS的混沌性降低。

2）当所选 f(a，xi)和 g(b，xi)是两个不同的一维混沌映射时，式（3）中定义的STBCS具有交换性。使用不同的 f(a，xi)和g(b，xi)可生成大量新的混沌映射，这些新的混沌映射和它们对应的种子混沌映射是完全不同的，且总是具有更复杂的混沌行为。

此外，图2中STBCS的结构可以进一步扩展为三个或更多个种子映射。如图3所示。

图3 多种子映射的混沌系统构造原理

图3 为具有N个种子映射的STBCS扩展原理示意图。每一次迭代会将输入xi同时反馈到N个种子映射中，即 f1(a1，xi)，f2(a2，xi)，…，fN(aN，xi)，并且对所有种子映射的输出进行正弦变换，这为用户选择种子混沌映射提供了灵活性，生成的混沌映射具有更复杂的混沌行为和参数设置，因此它们具有更好的混沌性能，并产生更多的随机的、不可预测的输出序列。然而利用更多的种子映射可能会带来一些负面影响，比如时间延迟，实施困难和分析复杂等问题。

3.2 基于正弦变换混沌系统产生混沌映射方法的一个例子

本节将介绍一个现有的一维种子混沌映射生成的混沌映射的例子。下面将以Tent-Sine（TS）映射为例对基于正弦变换的混沌系统进行说明。

定义：当选择种子映射 f(a，xi)为Tent映射，g(b，xi)为Sine映射时，可以生一个称为Tent-Sine（TS）的新混沌映射，并将其控制参数a、b分别设置为r和1-r，则TS混沌映射可定义如下：

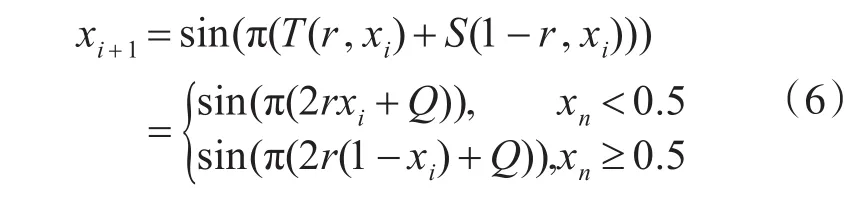
其中 Q=(1-r)sin(πxi)。

3.3 改进的延时TS混沌的新型映射

延时TS混沌映射的表达式如下：

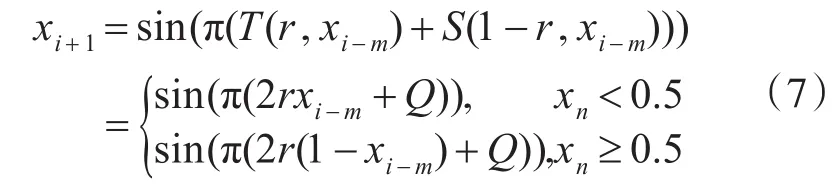
其中 Q=(1-r)sin(πxi-m)，m=1，2，…，8 ，m 表示TS混沌映射延时的单位数，如当m=1时表示TS混沌映射延时一个单位。

为了便于理解，下面也给出种子映射Tent映射、Sine映射的延时表达式：

1）延时Tent映射的表达式：

2）延时Sine映射的表达式：

4 实验结果及性能分析

基于正弦变换混沌系统生成的Tent-Sine的延时混沌映射具有更好混沌性能。为了证明该性质，本节评估了TS延时混沌映射，并将原始未延时的、延时一到八个单位的新混沌映射进行比较和分析。具体从以下三个方面展开：分叉图、样本熵（Sample entropy，SE）［19］和 Kolmogorov熵（Kolmogorov entropy，KE）［20］。

4.1 分叉图—混沌性和鲁棒性分析

分叉图用于描述动态系统的输出范围随参数的变化情况。如图4（a）为原始未延时TS映射的分叉图，图4（b）～（i）分别为TS映射延时一到八个单位时，其输出范围随控制参数r变化的分叉图。

从图中可以看出，未延时的TS混沌映射在2＜r＜4时不具备鲁棒性的混沌行为，而经过延时的TS混沌映射在整个参数范围内都具有良好的鲁棒性和混沌性。

4.2 样本熵（SE）—复杂性分析

样本熵（SE）来源于近似熵，它是时间序列复杂度的度量，可用来描述由动态系统产生序列的相似性。样本熵的值越大，其规律程度越低，即动态系统越复杂。如图5所示，对未延时TS混沌映射、延时一到八个单位的TS混沌映射的SE曲线图作对比。图5（a）为原始未延时TS映射的SE曲线图，图5（b）～（i）分别为TS混沌映射延时一到八个单位的SE曲线图。

从图中可观察到，未延时的TS映射，当r≈0.04时 ，SE=0；当 0.04＜r≤0.92时 ，SE＜1；当0.92＜r≤1时，SE＞1。TS映射延时一个单位时，当0＜r≤1时，SE＜0.5。TS映射延时两个单位时，当0＜r≤0.18时，SE≤1；当 0.18＜r≤1时，SE＞1。TS映射延时三个单位时，当 0＜r≤0.1且0.2＜r≤1时，0.5＜SE≤1；当 0.1≤r＜0.2时，SE＞1。TS映射 延 时 四 个 单 位 时 ，当 0＜r≤0.2时 ，0.6＜SE＜0.8；当 0.2＜r≤1时，SE≤0.6。TS映射延时五个单位时，当 0＜r≤0.2时，0.5＜SE＜0.6；当 0.2＜r≤1时，0.3＜SE＜0.5。TS映射延时六个单位时，当0＜r≤1时，0.4＜SE＜0.5。TS映射延时七个单位时，当0＜r≤1时，0.3＜SE＜0.4。TS映射延时八个单位时，当0＜r≤1时，0.2＜SE＜0.3。从以上分析来看，当TS映射延时两个单位时，其SE值最大、大于1的范围更广且相对将稳定，这就意味着提出的延时两个单位的TS映射比原始未延时的、延时其他单位的TS映射规律程度低，即动态系统更具复杂性。

图4 TS映射的分叉图

图5 TS映射的SE曲线图

4.3 Kolmogorov熵—不可预测性分析

KE是一种度量熵，它为有限对象的随机性提供了数学解释。它可用于使用其先前t次输出轨迹需要多少额外信息去预测第（t+1）次输出。确定的KE意味着需要额外的信息来预测轨迹，KE越大表示所需的信息越多。因此，具有正KE值的动力系统被认为是不可预测的，而更大的KE意味着更好的不可预测性。如图6对由STBCS生成的原始未延时的TS混沌映射、延时一到八个单位的TS混沌映射的KE曲线图作对比。图6（a）为原始未延时的TS混沌映射的KE曲线图，图6（b）～（i）分别为TS混沌映射延时一到八个单位的KE曲线图。

图6 TS映射的KE曲线图

从图中可以看出，未延时的TS映射，当0＜r≤0.04时，KE=0；当0.04＜r≤0.8时，KE＜1；当0.8＜r≤1时，KE＞1。TS映射延时一个单位时，当 0＜r≤0.8 时 ，KE＜0.5 ；当 0.8＜r≤1 时 ，0.5＜KE＜0.7。TS映射延时两个单位时，当0＜r≤0.22时，0.2＜KE＜0.8；当 0.22＜r≤1时，0.8＜KE＜0.9。TS映射延时三个单位时，当0＜r≤0.1 时 ，0.5＜KE＜0.8 ；当 0.1＜r≤1 时 ，0.8＜KE＜0.9。TS映射延时四个单位时，当0＜r≤0.1 时 ，0.5＜KE＜0.7 ；当 0.1＜r≤1 时 ，0.7＜KE＜0.8。TS映射延时五个单位时，当0＜r≤0.1 时 ，0.5＜KE＜0.7 ；当 0.1＜r≤1 时 ，0.7＜KE＜0.8。TS映射延时六个单位时，当0＜r≤0.1 时 ，0.5＜KE＜0.6 ；当 0.1＜r≤1 时 ，0.6＜KE＜0.7；TS映 射 延 时 七 个 单 位 时 ，当0＜r≤0.1 时 ，0.4＜KE＜0.5 ；当 0.1＜r≤1 时 ，0.5＜KE＜0.6。TS映射延时八个单位时，当0＜r≤0.1 时 ，0.3＜KE＜0.4 ；当 0.1＜r≤1 时 ，0.4＜KE＜0.5。从以上分析来看，当TS映射延时两个单位、三个单位时，其KE值较未延时稳定，且相对延时其他单位的TS映射KE值更大。故延时两个或三个单位的TS映射具有更好的不可预测性，其混沌性能更优。

4 结语

本文提出了一种基于正弦变换混沌系统产生的Tent-Sine混沌映射的延时混沌映射。它首先是对现有的种子映射Tent映射、Sine映射的输出进行线性加权组合，其次对组合的输出结果进行正弦函数变换，产生出Tent-Sine混沌映射，再对产生的Tent-Sine混沌映射分别进行一到八个单位的延时处理，得到延时后的新混沌映射，最后通过Matlab软件仿真出各个延时的Tent-Sine混沌映射的分叉图、样本熵曲线和Kolmogorov熵曲线，并对它们进行一系列的测试、分析和对比。实验结果表明，文章中提出的延时Tent-Sine混沌映射比未延时的Tent-Sine混沌映射有更大的混沌范围，延时两个单位的Tent-Sine混沌映射样本熵的值大于1的范围比原始未延时的、延时其他单位的映射均有所扩大，延时两个和三个单位的Tent-Sine混沌映射其Kolmogorov熵的值更具稳定性。延时Tent-Sine混沌映射更具鲁棒性，复杂性更高，具有更好的不可预测性。