μ测度点以及乘积空间X×X上概率测度的两个性质

陈 平

(江苏第二师范学院 数学与信息技术学院,江苏 南京 210013)

本文的主要工作受益于文献[5]中第六节内容的启发。在该文献中，作者证明了乘积空间Hn×Hn上概率测度的两个性质定理，其中Hn指Heisenberg群(Hn,d,L2n+1)，这里d指测地距离，L2n+1为2n+1维Lebsegue测度。这两个性质定理是证明Heisenberg群上的最优运输问题中最优映射的存在性的重要基础定理[5]。在该文献的第六节第一段结尾部分，作者提及当Heisenberg群推广至任意可分的加倍的度量测度空间(X,d,μ)时，乘积空间X×X上概率测度应该具有类似的性质，但作者并未给出证明。为此，本文详细证明了这两个性质定理。我们将使用如下记号：(X,d,μ)为可分的加倍的度量测度空间，简记为X，其中加倍是指存在常数c0>0，使得对任意x∈X和r>0有μ(B(x,2r))c0μ(B(x,r))成立。P(X)表示X上的概率测度。如果ν,μ∈P(X)满足如下性质：对集合A⊂X，如果μ(A)=0，则ν(A)=0，那么称测度ν关于测度μ绝对连续，并记为ν<<μ。对与给定的的映射T:X→X以及μ∈P(X)，T#μ为X上的一个概率测度，定义如下:T#μ(A)=μ(T-1(A))，其中A⊂X为任意Borel集合。关于Newton空间等更多的度量测度空间的相关知识可以参阅文献[1、2、7、8]。

1 μ测度点的定义及性质

在证明乘积空间X×X上概率测度的性质定理之前，我们首先给出(X,d,μ)上函数和集合的μ测度点的定义，这一概念是Heisenberg群上函数和集合的Lebsegue点的推广。此外，在本节中我们还讨论了函数和集合的μ测度点的性质。

定义1.1(函数的μ测度点) 设(X,d,μ)是一个具有加倍测度的度量空间，f:X→[0,+)为μ-局部可和Borel函数，如果有

成立，则称点x∈X为函数f的μ测度点。函数f的全体μ测度点组成的集合记为Mea(f)。

定义1.2(集合的μ测度点) 设E⊂X，如果点x∈E是集合E的特征函数χE的μ测度点,则称点x称为集合E的μ测度点。集合E的全体μ测度点组成的集合记为Mea(E)。

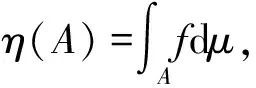
如下两个引理分别说明函数和集合的μ测度点性质。

引理1.4如果f∈L1(X,d,μ),则μ(XMea(f))=0。该式说明μ几乎处处x∈X是函数f的μ测度点。

证明：对任意x∈X和r>0定义如下函数

和

要证明命题成立，仅需证明对于μ几乎处处x∈X有Tf=0成立。

取λ>0，n为正整数，因为连续函数族C(X,d,μ)是函数族L1(X,d,μ)的稠密子集，因此存在g∈C(X,d,μ)使得||f-g||L1(X,d,μ)<1/n取h=f-g，因为g连续，因此对任意给定的x∈X，有

将最后一步等式右侧第一项记为(Mh)(x)，则有(Th)(x)(Mh)(x)+|h(x)|，∀x∈X。此外，由TrfTrh+Trg可知

因此

{x:(Tf)(x)>2λ}⊂{x:(Mh)(x)>λ}∪{x:|h(x)|>λ}

(1)

将(1)中右侧的并集记为E(λ,n)，分别估计(1)中右侧两项的μ测度。因为空间(X,d,μ)可分且测度具有加倍性质，因此文[6]中引理7.3成立，仅将第三条结论修改为μ(W)事实上，因为其中B(xi,3ri)，i∈S不相交，所以μ(W)进一步的，类似于文[6]中定理7.4的结论也成立，即

μ{x∈X:(Mh)(x)>λ}

(2)

此外，令E={x∈X:|h(x)>λ|},则有λμ(E)因此

μ(E)λ-1‖h‖L1(X,d,μ)

(3)

由上述(2)和(3)可得

μ(E(λ,n))

(4)

注意到(1)的左侧与n无关，因此

引理1.5设E⊂X，则μ(EMea(E))=0，即对于E中μ几乎处处的x，x是集合E的μ测度点。此外有下式成立:

(5)

证明：因为χE∈L1(X,d,μ)，由定义1.1，引理1.4可知,对于μ几乎处处x∈X，有

因此

从而命题得证。

2 乘积空间X×X上概率测度的两个重要性质

基于上一节中的定义，我们给出如下两个性质定理。这两个定理对于我们研究一般度量测度空间上最优运输问题[3、4、5、7、8]解的存在性，尤其是最优映射的存在是至关重要的。

1.y∈B(y′,r′)⊂⊂B(y,r)，

2.x∈Mea(ρ)并且ρ(x)<+，

3.x∈Mea(ρ′)并且ρ′(x)<+，

其中ρ和ρ′分别表示测度(π1)#γ和测度(π1)#γ|(X×B(y′,r′))关于测度μ的密度。

γm,k:=γ|(X×B(ym,rk))，

并将测度(π1)#γm,k关于测度μ的密度记为ρm,k，此外设

Am,k:=X(Mea(ρ)∩Mea(ρm,k)∩{ρ<+})

以及Dm,k:=[X(Mea(ρ)∩Mea(ρm,k)∩{ρ<+}∩{ρm,k>0})]×B(ym,rk)，我们首先证明γ(Dm,k)=0。

由引理1.4以及定义1.3中密度的非负性可得

μ(Am,k)μ(X(Mea(ρ))+μ(XMea(ρm,k))+μ({ρ<+})=0，

因为(π1)#γ<<μ，所以

(π1)#γ(Am,k)=0，

(6)

又因为

γ({ρm,k=0}×B(ym,rk))=(π1)#γ({ρm,k=0})=0,

(7)

所以由上述(6)和(7)可知：

γ(Dm,k)(π1)#γ(X(Mea(ρ)∩Mea(ρm,k)∩{ρ<+}∩{ρm,k=0}))

(π1)#γ(Am,k)+(π1)#γ{ρm,k=0})=0

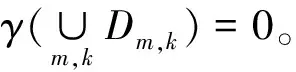
定理2.2设γ∈P(X×X)满足(π1)#γ<<μ。假设γ集中在σ紧集Γ上。对任意x∈X和r>0，令

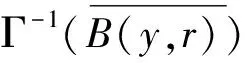
(8)

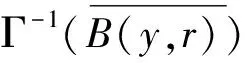
证明：证明依赖于空间X的可数覆盖以及测度μ的加倍性质。证明过程可以参阅文[5]中的引理6.2。令

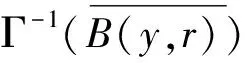
右侧集合的μ测度为零。因为(π1)#γ<<μ，因此γ(A)(π1)#γ(π1(A))=0。