双目标模式下芜湖市中心城区公园数量和规模的优化
彭 杰, 梁栋栋, 吴 旭, 占得龙, 何强弟
(1.安徽师范大学 地理与旅游学院,安徽 芜湖 241002;2.安徽师范大学 地理大数据研究中心,安徽 芜湖 241002;3.安徽师范大学 计算机与信息学院,安徽 芜湖 241002)
目前全世界城市人口已经超过了总人口的一半,预计到2050年全球城市人口将达到总人口的70%左右[1]。在城市化的快速进程中,绿地和水体已被证明具有降温增湿、调节局地小气候、缓解城市内涝等多种生态功能,也对缓解城市热岛效应有重大作用,但目前城市绿色空间不断地被城市建筑等不透水面取代,这与居民不断增长的对绿地需求之间的矛盾日益加剧[2-4]。城市公园作为城市中主要的自然景观元素和休闲游憩场所,在缓解这些矛盾过程中起着重要的作用[5-7]。在关注城市公园的休闲游憩、净化环境和调节气候功能的同时,不再局限于其数量和质量,而更加关注居民能否方便快捷地进入公园进行游憩活动以及公园分配的合理性问题[8-11]。如何实现城市公园数量和规模的合理分配,需要新建多少数量多大规模的城市公园才能够服务更多的居民,对于这些问题的研究,先前的理论、方法和尺度均难以回答这些问题。
目前对城市公园布局的合理性评价主要考虑其可达性。城市可达性的概念最初是在1959年由Hansen提出的,主要探讨了城市土地规划和可达性之间的影响与联系,可达性常用距离、时间和费用等指标来衡量[12-15]。Handy认为城市公共空间的可达性是评价空间布局合理性的重要因素之一[16]。Alexis Comber综合经济等相关方面的数据,对英国各个种族和宗教抵达绿地系统的可达性进行定量研究,从而对绿地系统的服务进行测评[17]。近年来,随着对公园重要性认知的提升,我国的专家学者对于城市公园可达性的探究和讨论也逐渐增加。李文等以哈尔滨为例,根据城市公园的可达性及其服务效率,得出哈尔滨城市公园分布不均衡且总量缺乏的结论[18]。姚雪松等则以长春市为例,应用GIS分析老年人口密度,通过SPSS分析老年人的活动需求和影响因素,来评价公园设施可达性和满意度[19]。陈秋晓则基于空间公平视角,对居民能够使用公园绿地的选择机会的空间分布情况进行统计,利用GIS工具在精细尺度上对城市公园绿地可达性进行测量[20]。这些可达性计算通常将将实体的城市公园抽象为点、线、面[21],现有的研究多以公园几何中心或质心来表示,而城市公园常表现出具有一定大小的面状结构,由于城市公园面积和形状的影响,这些方法会低估城市公园的可达性[2]。同时,城市公园的可达性并不能作为判断城市公园布局好坏的唯一指标,过渡强调可达性反而会导致大量修建城市公园,盲目追求城市公园数量和规模来提高可达性。本文以芜湖市中心城区为例,一方面考虑城市公园数量和规模不断增加有利于提高可达性,降低居民到公园的平均最近距离,另一方面考虑到过多数量和过大规模的城市公园会对交通造成干扰,不利于城市居民出行,通过综合权衡可达性与干扰性,得到芜湖市城市公园的最佳数量和规模,以期为以后的城市公园规划提供参考。
1 研究区概况

图1 芜湖市中心城区公园分布图Fig.1 Wuhu city central city park distribution map
芜湖市地处安徽省东南部,南倚皖南山系,北望江淮平原,属亚热带湿润季风气候,光照充足,雨量充沛,四季分明。据《芜湖统计年鉴(2016)》,芜湖市总面积6026km2,总人口369.6万人,人均GDP为84000元,下辖4个市辖区、4个县、2个经济开发区。本文选择人口较为密集的4个市辖区为研究对象,分别为鸠江区、弋江区、三山区和镜湖区,总面积为1491km2,常住总人口165.2万人,市辖区公园总面积约为18.22km2,包括赭山公园(4A)、滨江公园(3A)和汀棠公园(3A)这3个A级公园,总面积为2.57km2,还包括29个非A级公园,总面积为15.65km2,如图1所示。
2 研究方法
传统公园布局评价模式经常将小的公园用点来表示[21],然而它的规模大小不可忽略,这些公园的规模一方面决定了它的服务范围,一方面又会造成对周围交通的干扰,因此在规划这些公园时要充分权衡这些公园的数量与大小,既要满足居民需求,减少居民到公园的最近距离,又要降低这些公园对交通造成的干扰。
双目标模型是Masashi提出的关于确定城市有限规模设施数量和大小的一种方法,这里并不考虑这些设施具体的分布位置,而是考虑在一定范围内需要多少个、多大的设施才更加合理[22-23]。本文将Masashi的双目标模式运用到芜湖市公园优化研究中,并与芜湖市中心城区公园的数量和规模现状值进行比较,试图寻求芜湖市中心城区公园最佳数量和规模的组合。使用传统的双目标模式局限于把城市公园的大小都分成相同的面积,这并不符合城市中公园规模的实际情况,基于社会的需求与传统方法的不足,将公园分为A级与非A级两种类型,新的双目标模式一方面计算居民到最近公园的平均最近距离,代表居民到公园的可达性,另一方面计算公园与城市范围内随机一条交通线相交的概率,代表它对交通流的干扰度。通过权衡居民到公园的平均最近距离与公园可能对交通造成的干扰度,以此来确定城市公园最佳数量和规模的组合,目的是降低居民到公园的平均最近距离和城市公园可能对交通造成干扰的概率。
2.1 居民到公园的平均最近距离
根据城市公园的规模将芜湖市的公园分为非A级和A级两种类型,分别用半径为d1和d2的圆来表示,假设n1个非A级公园和n2个A级公园随机分布在城市中,由于这里并不考虑具体分布在什么位置,所以将整个市区面积转换成半径为a的圆来表示以方便计算。让R成为在城市中除公园以外的一个随机选择的点到它附近最近公园的距离,R是离公园最近点的距离,F(r)成为R的累计分布函数,也就是半径为d1和r+d1的两个圆的圆环之间至少包括一个非A级公园,或半径为d2和r+d2的两个圆的圆环之间至少包括一个A级公园的概率,区域S包含x个随机分布公园的概率由泊松分布给出,通过P(x,S)表示:
(1)
式中,S为研究区公园总面积,x为公园个数,ρ为公园密度。市区总的公园面积为
(2)
式中,n1为非A公园的数量,d1为非A级公园的半径,n2为A级公园的数量,d2为A级公园半径。由于公园是随机分布的,所以R的累计分布函数:
(3)
式中ρ1为非A级公园在城市中的密度,ρ2为A级公园在城市中的密度。对F(r)关于r微分得到概率密度函数f(r):
f(r)=2π{ρ1(r+d1)-ρ2(r+d2)}exp[-πr{ρ1(r+2d1)+ρ2(r+2d2)}]
(4)
平均最近距离E(R):
(5)
式中n1、n2、d1、d2均与式(2)一致。
2.2 公园对交通造成干扰的概率
假设P为城市内一条随机的交通线至少与一个公园相交的概率,这个概率越大表示公园对交通的阻碍可能就越大,这组随机的交通线被定义为
(6)
式中,P为这组交通线与公园相交的概率,θ表示这组交通线的随机角度。分别用A、A0、A11、A12、A21、A22、A23表示几种相交类型的交通线:A0表示与城市相交的交通线,A表示至少与一个公园相交的交通线,A11表示与一个非A级公园相交的交通线,A12表示与一个A级公园相交的交通线,A21表示与两个非A级公园相交的交通线,A22表示与两个A级公园相交的交通线,A23表示与A级公园和非A级公园相交的交通线。
然后给出交通线相交的概率P:
(7)
式中,A为至少与一个公园相交的交通线,A0表示与城市相交的交通线。m(A0)就相当于交通与有界凸集相交,也就是等于它的周长:
m(A0)=2πa
(8)
式中,a为城市半径,根据容斥(inclusion-exclusion)原理[24-25],测得m(A):
(9)
然后测得A11、A12、A21、A22:
m(A11)=2πd1
(10)
m(A12)=2πd2
(11)
(12)
(13)
式中d1、d2与式(2)相同,t是城市中两个随机选择的公园之间的距离,A23是通过两个公园的内部L(C1,C2)和外部L(C12)覆盖的长度确定。
(14)
由于t是城市中两个随机选择的公园之间的距离,a为城市半径,t用E(T)表示:
(15)
将上述公式中的所有t用E(T)来代替,所以,
(16)
因此,
(17)
式中,n1、d1、n2、d2与式2相同,E(T)为城市中两个随机选择的公园之间的距离。
3 两种模式结果
3.1 单目标模式结果

(a)E(R)随n1的变化 (b)P随n1的变化图2 E(R)与P随非A级公园数量n1的变化函数曲线Fig.2 E(R) and P as a function of the number of non-A-level parks n1
查阅《芜湖统计年鉴(2016)》,可知芜湖市辖区常住总人口165.2万人,按标准人均13.5m2的城市公园面积,芜湖市总的公园面积至少要有22.302km2,目前芜湖市中心城区的总面积为1491km2,由于我们并不考虑这些公园具体分布位置,所以用圆来表示其范围,半径a=21.785km。这里我们假设A级公园的数量和半径已知,随机选择n2=3,d2=0.5km;n2=3,d2=1.0km;n2=4,d2=0.5km;n2=5,d2=0.5km和n2=7,d2=0.7km五种情况,根据式(5),模拟出图2(a)中5条E(R)随n1变化的曲线,可以发现随着非A级公园数量n1的增加,平均最近距离E(R)在不断减小,居民可达性更高;根据式(17)得到图2(b)中5条P随n1变化的曲线,发现公园可能对交通造成干扰的概率P随非A级
公园数量n1的增大而增大。同理先假定非A级公园的数量和规模后可以发现,E(R)随着A级公园数量n2的增加而减少,而P随着A级公园数量n2的增加而增大。
3.2 双目标模式结果
目前芜湖市已有A级公园3个,非A级公园29个,A级分别是赭山公园、滨江公园和汀棠公园,市区公园总面积约为18.22km2,其中A级公园面积总和约为2.57km2,平均半径为0.52219km,非A级公园的总面积为15.65km2,平均半径为表中n2为A级公园的数量,d2为A级公园的半径。

表1 各种数量和规模下的模拟次数和有效结果
0.44719km。根据式(5)和式(17)可以得出目前芜湖市公园E(R)与P的现状值分别是E(R)=3.026647115,P=0.543258501。同样根据式(5)和式(17),从n2=1,d2=0.4km开始模拟,随着A级公园数量n2的增加,半径d2在减小,要保证d2>d1,如表1所示,故模拟截止到n2=10。本次共进行了74次有效模拟,每次模拟产生了13至19种有效结果,总共产生1377种结果。

图3 n2=1时E(R)与P的分布函数Fig.3 The distribution function ofE(R) and P when n2=1
为了更加直观的展示上述结果,将A级公园的数量n2从1到10变化产生的结果分成10幅图展示,如图3至图12,每幅图又包括d2从0.4到1.4km不同情况下的E(R)与P分布函数的若干条曲线。图3是当n2=1时,d2从0.4到1.4km的11条E(R)与P的分布曲线,每条曲线又包括非A级公园数量n1从10到100的变化,如d2=1.0这条曲线,最下方这点代表n2=1,d2=1.4,n1=10,d1=0.692792km这种公园数量和规模下E(R)与P的值。从图中可以发现对于任意一条曲线,n2和d2是固定的,随着非A级公园半径d1的增加,对交通干扰概率P在降低,而平均最近距离E(R)也在下降。从图3中发现当n2=1时,权衡各条曲线的E(R)与P,并没有明显点的值同时小于芜湖市当前已存在的E(R)与P值。图3中,n2=2随着d2的增加,E(R)与P函数曲线之间的间隔在增加,出现了大量小于现有条件下的E(R)与P值的点。继续比较图3至图12,n2等于其它值的情况,出现了大量E(R)与P同时小于现状值的点,也就是比目前更好的公园数量与规模的组合。

图4 n2=2时E(R)与P的分布函数
Fig.4 The distribution function ofE(R)andPwhenn2=1

图5n2=3时E(R)与P的分布函数
Fig.5 The distribution function ofE(R)andPwhenn2=3

图6n2=4时E(R)与P的分布函数
Fig.6 The distribution function ofE(R)andPwhenn2=4

图7 n2=5时E(R)与P的分布函数
Fig.7 The distribution function ofE(R)andPwhenn2=5

图8n2=6时E(R)与P的分布函数
Fig.8 The distribution function ofE(R)andPwhenn2=6

图9n2=7时E(R)与P的分布函数
Fig.9 The distribution function ofE(R)andPwhenn2=7

图10 n2=8时E(R)与P的分布函数
Fig.10 The distribution function ofE(R)andPwhenn2=8
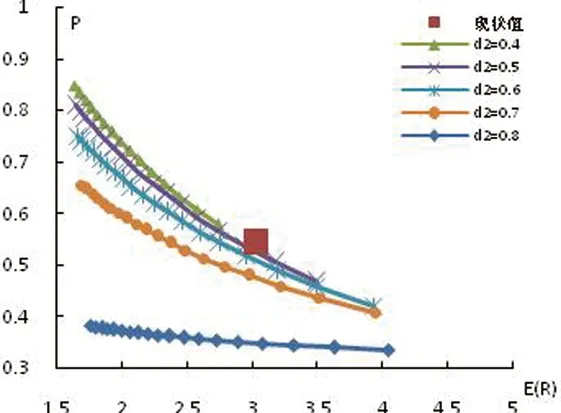
图11n2=9时E(R)与P的分布函数
Fig.11 The distribution function ofE(R)andPwhenn2=9

图12n2=10时E(R)与P的分布函数
Fig.12 The distribution function ofE(R)andPwhenn2=10
4 结果分析
4.1 单目标模式结果分析
通过单目标模式分析,得出居民到公园的平均距离E(R)与公园数量成反比,公园对交通可能造成的干扰概率P与公园数量成正比,公园数量增加,居民到公园平均最近距离减小,方便了居民到达公园,但公园数量的增加对交通可能造成的干扰度也增大,对交通流又会产生阻碍作用;反之公园数量减少,对交通干扰概率会降低,但居民到公园的平均最近距离就会随之增加,也会对居民日常生活造成极大的不便。因此单方面考虑居民到公园的平均最近距离或公园对交通可能造成的干扰概率都会造成另一个值过大,不能真正的方便居民的生活,必须要通过双目标模式综合考虑到公园的平均最近距离E(R)与对交通造成的干扰概率P,寻求最佳的公园数量与规模的组合。
4.2 双目标模式结果分析
通过双目标模式模拟大量的居民到公园的平均最近距离E(R)与公园对交通流可能造成干扰的概率P的函数曲线,如图3至图12获得了1377组有效的结果,通过对芜湖市现有公园状况下计算得到的E(R)与P进行比较,找出E(R)与P都小于现状值的n1、d1、n2、d2的组合,也就是最佳的非A级公园的数量与规模和A级公园的数量与规模。因此将这1377组模拟出来的E(R)和P直接与现状值相减,取E(R)与P同时小于现状值的点,同时根据2017年1月1日实施的《公园设计规范(GB 51192—2016)》,城市综合公园面积不应小于5hm2,因此直接排除面积小于5hm2的公园,也就是半径小于0.126km的情况。从表2至表10共有113种符合要求的n1、d1、n2、d2的组合。
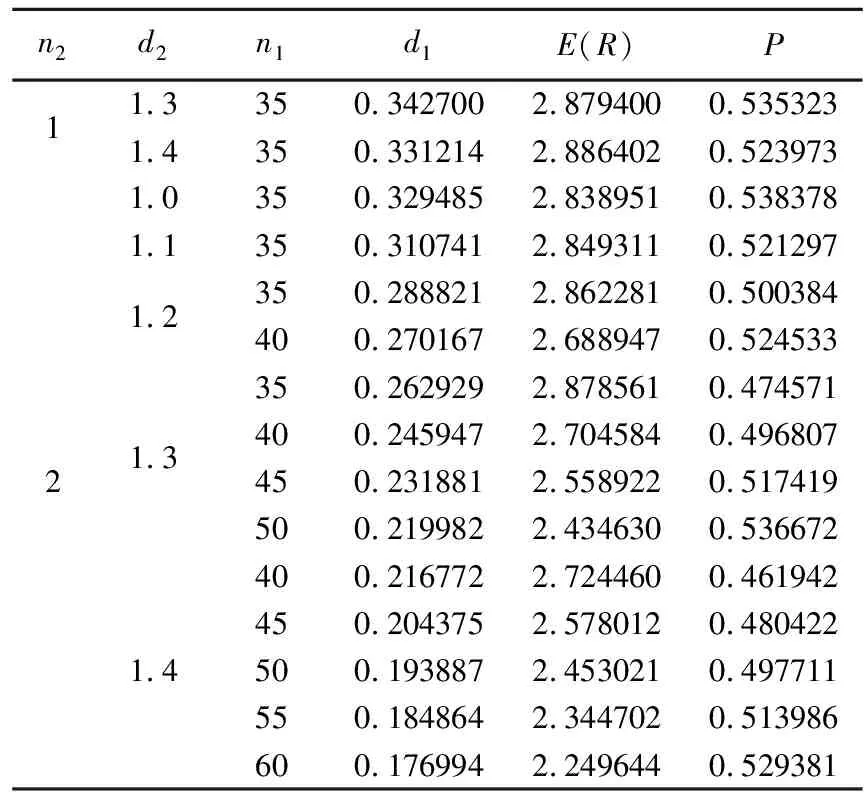
表2 n2=1和n2=2时符合要求的组合

表3 n2=3时符合要求的组合
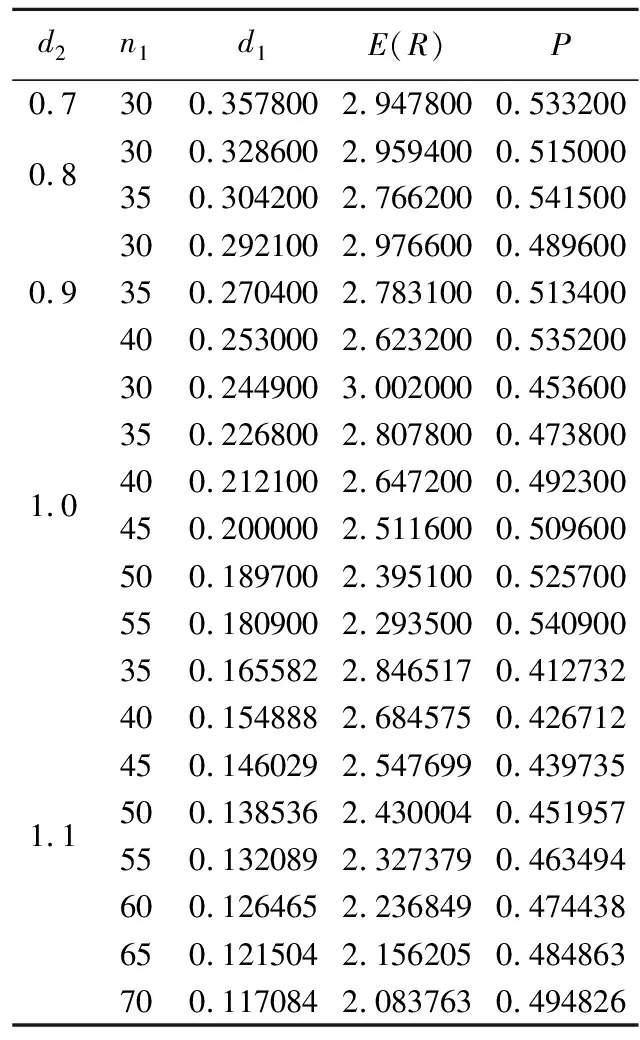
表4 n2=4时符合要求的组合
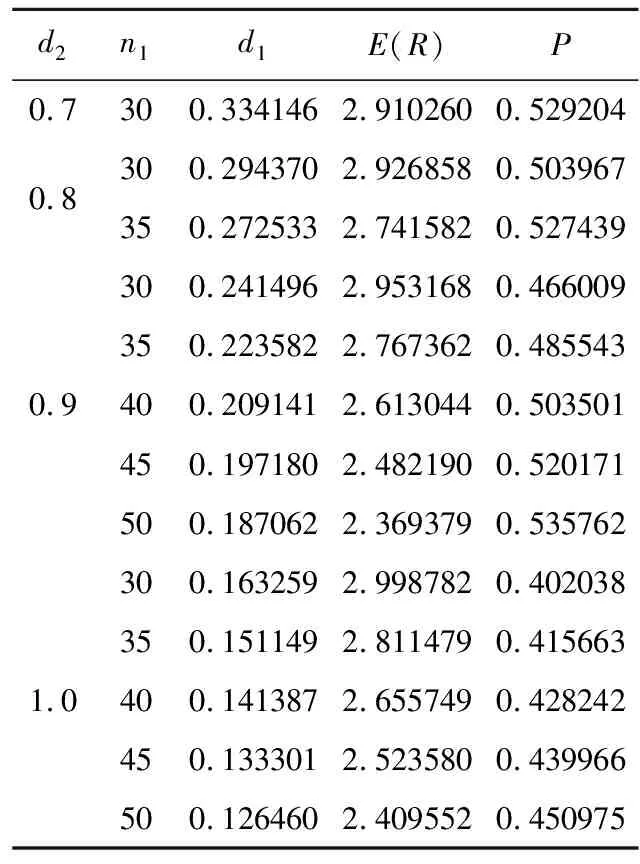
表5 n2=5时符合要求的组合

表6 n2=6时符合要求的组合

表7 n2=7时符合要求的组合

表8 n2=8时符合要求的组合
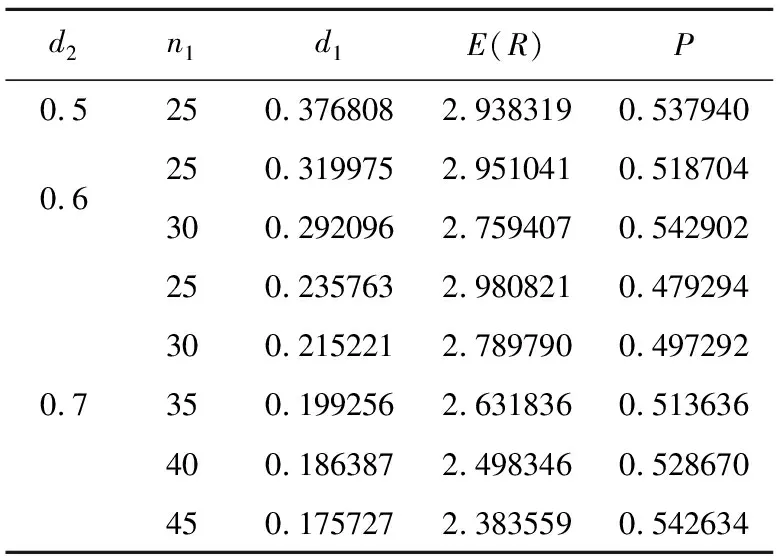
表9 n2=9时符合要求的组合
表2至表10中n1为非A级公园的数量,d1为非A级公园的半径,n2为A级公园的数量,d2为A级公园的半径。
以上的结果都为E(R)与P小于现状值的n1、d1、n2、d2的组合,从表2至表10观察可以发现n2与d2的所有符合要求的组合中非A级公园数量n1=35至55出现的次数最多,为了更加直观的显示,将这些结果分布展示在图13中,根据分布情况比较权衡E(R)与P,防止某一个值过大或过小,选出E(R)与P较好的4组数据,如表11所示。
通过表11中的四组最佳组合与现状值进行对比可以发现,这四组数据的平均最近距离E(R)以及对交通可能造成干扰的概率P的值明显都要小于目前芜湖市的现状值,继续进行比较可以发现,这四组数据中的A级公园的半径和数量都要大于芜湖市现有的A级公园的半径和数量,而非A级公园的半径要小于芜湖市现有的非A级公园的半径,但数量却要比现有的非A级公园的数量多得多。

表10 n2=10时符合要求的组合
5 结论与讨论
本文基于双目标模型计算芜湖市中心城区居民到公园的平均最近距离和公园可能对交通造成干扰的概率,寻求芜湖市最佳的公园数量和规模的组合,发现随着居民到公园的平均最近距离随公园数量和规模的增加而减小,公园对交通可能造成的干扰概率随公园数量和规模增大而增大,通过权衡居民到公园的平均最近距离和公园对交通可能造成的干扰概率模拟产生了1377种公园数量和规模组合,其中113种组合效果要优于芜湖市中心城区的现状值,并选取出4种最佳组合。通过研究发现这些最佳组合中A级公园的半径和数量都大于芜湖市现有的A级公园的半径和数量,而非A级公园的半径要小于现有的非A级公园的半径,但数量却要比现有的非A级公园的数量多,说明芜湖市目前的A级公园面积和数量都与最优数量和规模存在一定差距,而非A级公园的面积都比较大,但是数量上还明显不够,因此在芜湖市未来的公园规划发展中,为了降低居民到公园的平均最近距离,同时减少公园对交通流可能造成的干扰,发挥城市公园真正的价值,方便居民的出行,应当适当的扩大现有的A级公园的规模,同时再增加1到2个A级公园,对于非A级公园而言,可以向小而精的方向发展,满足基本功能的情况下,不需要追求过大的面积,而可以增加其数量,减少居民到公园的平均最近距离,又不会对交通流造成太大的干扰。

图13 所有符合要求值的分布Fig.13 All distributions that meet the required values

数据来源n2d2n2d2E(R)P模拟值41.1450.1460292.5476990.43973541.1500.1385362.4300040.45195751450.1333012.523580.43996651500.126462.4095520.450975现状值30.52219290.447193.0266471150.543258501
基于双目标模式寻求芜湖市中心城区公园的最佳数量和规模,为之后的公园规划提供了一些建议,但受制于模型不考虑公园分布具体位置这个前提的影响,为方便计算将芜湖市中心城区假设为一个等面积的圆,没能考虑城市的具体形状,因此本文未能给出这些模拟下得到的最佳数量和规模组合的公园在城市分布的具体位置,后续研究中可以运用元胞自动机等方法进行模拟仿真将通过双目标模式确定的公园在研究区内进行合理的空间分配。

