码头类型对大型船舶运动响应特性的影响研究

袁培银，王平义，刘添宇，赵 宇,3

(1. 重庆交通大学 河海学院，重庆 400074； 2. 重庆交通大学 航运与船舶工程学院，重庆 400074；3. 重庆交通大学 建筑与城市规划学院，重庆 400074)

0 引 言

随着经济的不断发展，人们收入不断增加，海上旅游业也不断兴旺，旅游船队的规模不断增大，内河与海上的旅游观光人数越来越多，如今，海上旅游已经成为欧洲以及亚洲人的一种时尚[1-3]。随着豪华游轮数量的增加及级别的提高，对大型船舶的系泊安全要求也越来越高，豪华游轮的系泊系统已成为船舶停靠和港口设计需要考虑的重要问题[4-6]。国内外对于船舶码头系泊的研究始于20世纪 90年代后期，于洋等[7]、吴小鹏[8]及A. R. SHASHIKALA等[9]采用物理模型试验、数值模拟的方法对影响船舶系缆力的海洋动力因素、船舶因素进行了研究；周宏康等[10]通过模型实验得到FSRU的运动响应和系泊缆张力；嵇春艳等[11]以码头系泊为研究对象，利用水动力分析软件AQWA，分析了不同浪向角作用下，系泊船舶的幅值响应算子和一阶波浪力，采用不同方式优化船舶系泊系统；H.W.LEE等[12]提出了一种应用柔性动力学的有限元方法，用于研究系泊缆索与海底的相互耦合作用，并将该方法应用到实际工程中；S. Y. LEE[13]提出了一种应用于海上浮动结构的新的导向桩码头系泊系统；陈里等[14]分析了滑坡涌浪作用下系泊船舶系缆力和撞击能的影响因素，探讨了在波高、水深等影响下系泊船舶系缆力和撞击能的变化规律，确定了滑坡涌浪对内河船舶系泊安全的影响程度。笔者针对码头与大型游船组成的靠帮系泊系统，编写了多浮体水动力分析程序，研究了船舶与码头间不同距离、不同形状的码头对系泊船舶的影响规律。研究方法及计算程序可推广至多个浮体运动规律研究中。

1 大型船舶码头系泊系统设计

1.1 大型船舶主尺度参数

采用方形码头及圆筒形码头这2种不同形状的码头对相同船舶进行系泊分析。船舶与码头系泊示意如图1，其主要尺度参数见表1。

图1 船舶与码头系泊示意Fig. 1 Diagrammatic sketch of wharf

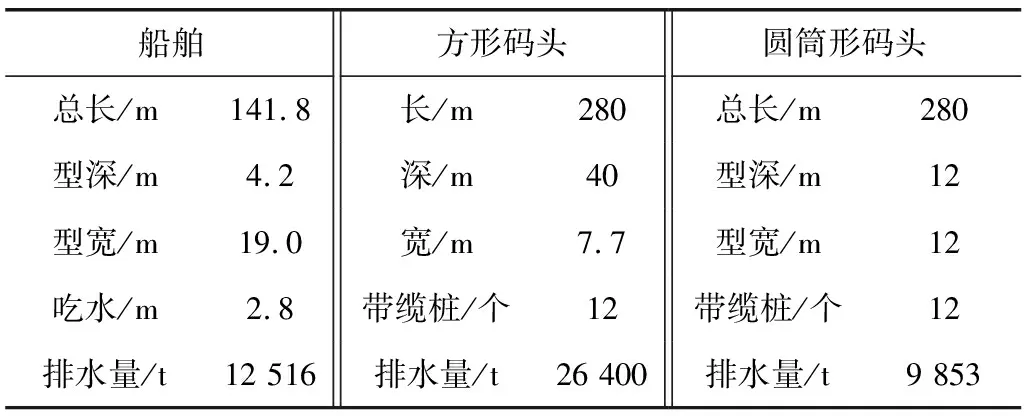
船舶方形码头圆筒形码头总长/m141.8长/m280总长/m280型深/m4.2深/m40型深/m12型宽/m19.0宽/m7.7型宽/m12吃水/m2.8带缆桩/个12带缆桩/个12排水量/t12 516排水量/t26 400排水量/t9 853

图2 船舶六自由度的RAO曲线Fig. 2 RAO curves of 6-DOF of ship

1.2 码头系泊系统布置设计

游船码头系泊共有8根系缆绳，其中船艏缆和船尾缆各2根，船中横缆4根交叉进行系泊。缆绳为尼龙材料制成，系缆绳直径为100 mm，最大拉力为140 kN。

1.3 环境载荷

笔者主要研究系泊船舶在风浪共同作用下的运动响应，风速为1.5 m/s，入射方向为30°，波浪以180°入射，有义波高为0.8 m。

2 船舶频域水动力性能影响因素

2.1 码头距离

图2为船舶六自由度幅值响应算子随着方形码头距离的不同而变化的情况。在计算过程中，船舶与方形码头距离分别为5、10、20、40、100、500 m。

从图2可以看出，码头距离的大小对旅游船六自由度幅值响应算子的变化影响较小。船舶六自由度的幅值响应算子的变化周期、变化趋势和峰值变化不明显。

2.2 码头形状

图3为船舶六自由度上的幅值响应算子随着不同形状码头而产生的变化情况。

图3 不同形状码头系泊时船舶六自由度RAO曲线Fig. 3 RAO curves of 6-DOF of ship in different wharfs

由图3可以看出，当船舶的运动周期为25 s时，不同形状的码头对船舶六自由度上的幅值响应算子影响是不同的，可以得出以下结论：

1)船舶纵荡，横荡和艏摇运动幅值随时间的增加一直呈现上升趋势，如图3(a)、(b)、(f)。在纵荡方面，在圆筒形码头的影响下船舶的运动幅值更小，说明在方形船舶影响下，船舶纵荡运动更加剧烈；在横荡方面，与纵荡运动相反，在方形码头的影响下船舶的运动幅值更小，说明船舶受到圆筒形码头的影响更大；在艏摇方面，方形码头和圆筒形码头对船舶的影响没有明显的变化。

2)船舶横摇和纵摇运动幅值随时间的增加都呈现先增加后减小的趋势，如图3(d)、(e)。在圆筒形码头的影响下，船舶的运动幅值更大，在横摇和纵摇运动上分别出现最大幅值，说明船舶横摇和纵摇运动幅值响应算子受圆筒型码头影响较方形码头影响大。

3)船舶垂荡随时间的增加呈现先减小后增大的趋势，如图3(c)；但是，在方形码头的影响下，船舶的运动幅值更小，说明船舶垂荡幅值响应算子受圆筒型码头影响较方形码头影响大。

3 船舶时域分析——系泊状态下

由船舶的幅值响应算子曲线(图2、图3 )可以看出，不同码头形状对船舶的频域结果的影响也不经相同。笔者选择船舶分别停靠方形码头和圆筒形码头来分析系泊船舶在时域内的运动响应问题。研究中，2种码头的系缆桩位置与缆绳的长度、材料、预张力等物理特性保持一致。在方形码头和圆筒形码头上的船舶系泊示意如图4。

图4 码头系泊示意Fig. 4 Schematic of wharf mooring

采用笔者自编的程序来求解船舶与系泊缆索的完全时域耦合关系，分析船舶在不同形状码头、相同系泊系统作用下，船舶六自由度运动响应情况(图5)，计算时间为3 h，时间步长为0.2 s。

图5 船舶六自由度响应曲线Fig. 5 Response curves of 6-DOF of ship

由图5可以看出：

1)分别系泊停靠在方形码头或圆筒形码头，船舶的运动频率基本一致。系泊在圆筒形码头时，船舶纵荡和垂荡的运动比较剧烈，最大变化幅值分别为1.2 m和0.2 m；系泊在方形码头时，船舶横荡的运动比较剧烈，最大变化幅值2.0 m。

2)分别在方形码头或圆筒形码头系泊下，船舶的运动频率基本一致。系泊在方形码头时，船舶纵摇和艏摇运动比较剧烈，最大变化幅值分别为0.4°和3.0°；系泊在圆筒形码头时，船舶的横摇比较剧烈，最大幅值为0.8°。

4 结 论

笔者以某大型游船为例，自编程多体水动力学文件，以码头及船舶之间的距离、不同系泊码头形状为变量，研究系泊船舶的水动力性能，得到以下结论：

1)船舶与码头间距在50～500 m范围内，码头间距对船舶频域内六自由度的幅值响应算子基本没有影响。

2)据对水动力特性的分析，圆筒形码头对船舶在横荡、垂荡、横摇和纵摇等运动起到一定的增幅作用，但增幅幅值较小；而圆筒形码头能大大地减小船舶纵荡。

3)完全时域耦合分析发现，船舶在运动过程中，运动频率保持一致。与方形码头系泊相比，船舶在圆筒形码头系泊作用下，横荡、纵摇和艏摇运动受到的影响较大；圆筒形码头可有效地减小船舶的运动幅值，而纵荡，垂荡和横摇运动较为平缓。

4)方形码头与圆筒形码头对船舶纵荡、横荡、垂荡、横摇、纵摇和艏摇运动的影响效果不同，如果注重船舶横荡运动幅值控制，应选用方形码头；如果注重船舶纵摇运动控制，应选用圆筒形码头。