基于TIN模型的三角形微分土石方计算方法研究

李华蓉 ， 陈 涛

(1. 重庆交通大学 交通土建工程材料国家地方联合工程实验室，重庆 400074；2. 重庆交通大学 土木工程学院，重庆 400074)

0 引 言

在工程中，土石方填挖量是一个非常重要的指标，它直接影响到工程的造价及预算。近年来，随着国民经济的快速发展和基础设施的不断加强，在土地管理、水利水电工程、道路选线、交通等领域，土石方量成为估算工程费用、方案优化设计以及施工进度控制等需要考虑的一个重要因素[1-3]。毛雪松等[4]还通过建立半填半挖路基下边坡模型，对坡积体的稳定性进行了分析。目前最常用的土石方计算方法为数字高程模型(DEM)法。很多土石方计算的研究基于DEM进行。朱连辉等[5]在流域土石方工程中运用了一种利用无人机采集数据生成DEM的快速土方测算方法。在其它领域中，I.A. THOMAS等[6]利用DEM模拟由微观形态主导的农业流域水文敏感区域效果显著。

根据地形模拟的方式，DEM法分为规则格网(Grid)法和不规则三角网(TIN)法。在Grid法中，当微分方格的边长足够小时，可以用方格4个顶点高程的加权平均值代替整个方格地形面的高程。据此求得的成果精度能够相对提高，而且计算模型比较简易。但是由于方格顶点的高程并不是通过实测获得，而DEM土方计算中地形模型的精度基本决定了土方的计算精度[7]，因此其成果精度的提高始终存在瓶颈。TIN以其对地形细部结构的高精度描述特点，极大的弥补了Grid在地形模拟方面的缺陷。但是TIN利用大面积几何图形投影构成的几何体计算土石方，因地形的不规则起伏不可避免地造成模型误差。为解决这一问题，将几何微分思想引入TIN法中，通过细化模拟的几何体，从而更精确地逼近实际地形，不仅能够简化计算模型的复杂度，还能减小模型误差、提高成果精度。笔者利用这一思想，对TIN中的三角形进行微分，通过微分三棱柱计算土石方，提出了基于TIN模型的三角形微分土石方计算方法。

1 基于TIN模型的三角形微分土石方计算方法

在常用的基于离散点的土石方计算方法中，计算模型产生的误差主要来源于将不规则地形用规则几何形体进行模拟。在TIN模型中，采用实测三角形模拟地形表面，在一定程度上减小了地形模拟失真导致的误差。但在实际工程中，为了减少外业的工作量，对于地形起伏不大的区域高程点分布较为稀疏，造成了以大面积三角形面片模拟地形的情况，在土石方的计算中仍然会降低计算结果的精度。模拟地形的几何图形面积对成果精度的影响在Grid法中就有直观的体现，理论上几何图形面积越小，成果的精度将会越高。如果能够基于TIN模型，引入Grid法中的微分思想，当三角形的面积足够小时就能够进一步的提高计算成果的精度。赖鸿斌等[8]曾提出过一种利用TIN和Grid的混合模型计算填挖方量的方法；田旦等[9]介绍的一种提高方格网土石方计算精度的方法也是首先利用TIN建立测区的DEM，同样是TIN和Grid的混合运用。

基于TIN模型的三角形微分土石方计算方法的思想是先由离散点构建TIN模型，然后在TIN模型的基础上将由离散点构成的三角形不断进行分割，直至连续减小三角形面积而土石方计算的结果趋于稳定。与Grid法不同的是，利用该方法，微分三角形并非通过减小边长实现，而是对面积进行分割。

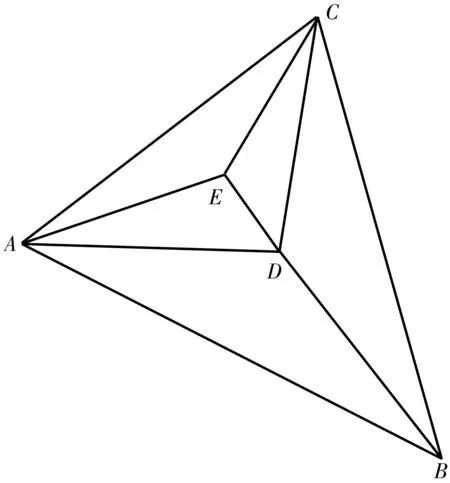
图1 三角形分割示意Fig. 1 Triangle segmentation schematic

该方法中，三角形分割基于已经构建好的TIN模型，其分割思想如图1。△ABC由离散点直接构成。设其顶点坐标分别为A(X1，Y1，H1)、B(X2，Y2，H2)，C(X3，Y3，H3)，当△ABC需要进行分割时，由式(1)求得其重心坐标D(XD，YD，HD)：

(1)

然后得到△ABD, △BCD和△ACD。如果△ACD仍需进行分割，同理求得其重心E的坐标，将△ACD继续分割为3个新的三角形。对其它三角形同样如此，直至所有三角形的面积小于阈值。由离散点构成的三角形地形面可以近似看作是连续变化的，因此由3个顶点求得的重心坐标具有较高的精度。同时，由原三角形的顶点和重心构成的3个新三角形的面积相等，保证了测区范围的平均分割，而在程序中判断是否继续分割的条件亦为三角形的面积。另外，在三角形中重心到3个顶点距离的平方和最小，这也在一定程度上保证了重心三维坐标的求取精度。

在进行土石方量的计算时，由于微分三角形的面积非常小，可以引入微分计算的思想。以每个微分三角形的重心点高程作为整个微分三角形面的高程，以微分三角形投影到设计高程面构成的正三棱柱体积计算填挖方量，类似于徐树坤等[10]提出的将空间体积转化为平面上求取面积近似定积分的思想。这种计算方法从实施上看仍然以三角形模拟地形面，按几何体体积进行计算，但不同的是，此时的微分三角形面积非常小，根据微分的思想以及高精度土石方工程中对填挖方量计算精度的要求，可以以点代面进行计算。

综合而言，利用基于TIN模型的三角形微分法计算土石方量的具体流程如图2，算法步骤如下：

步骤1：利用野外实测离散点数据，按照Delaunay三角形构建原则建立TIN模型，并将TIN模型中的三角形存储于待分割三角形线性表中。

步骤2：获取三角形面积阈值，按照待分割线性表中三角形的存储顺序，遍历待分割三角形。

步骤3：判断三角形面积和所取阈值的大小关系。当三角形面积大于阈值时，求取其重心三维坐标对其进行分割，并同时存储生成的3个新三角形于待分割线性表中。

步骤4：当待分割三角形面积小于阈值时，将此三角形存储于分割完成后的微分三角形线性表中，并遍历下一个待分割三角形，回到步骤3。

步骤5：按照步骤3、步骤4，遍历并分割所有待分割三角形，使得所有微分三角形的面积小于或等于阈值。

步骤6：遍历分割完成后的微分三角形，以微分三角形的重心点高程代替三角面的高程，利用微分三棱柱求得土石方量。

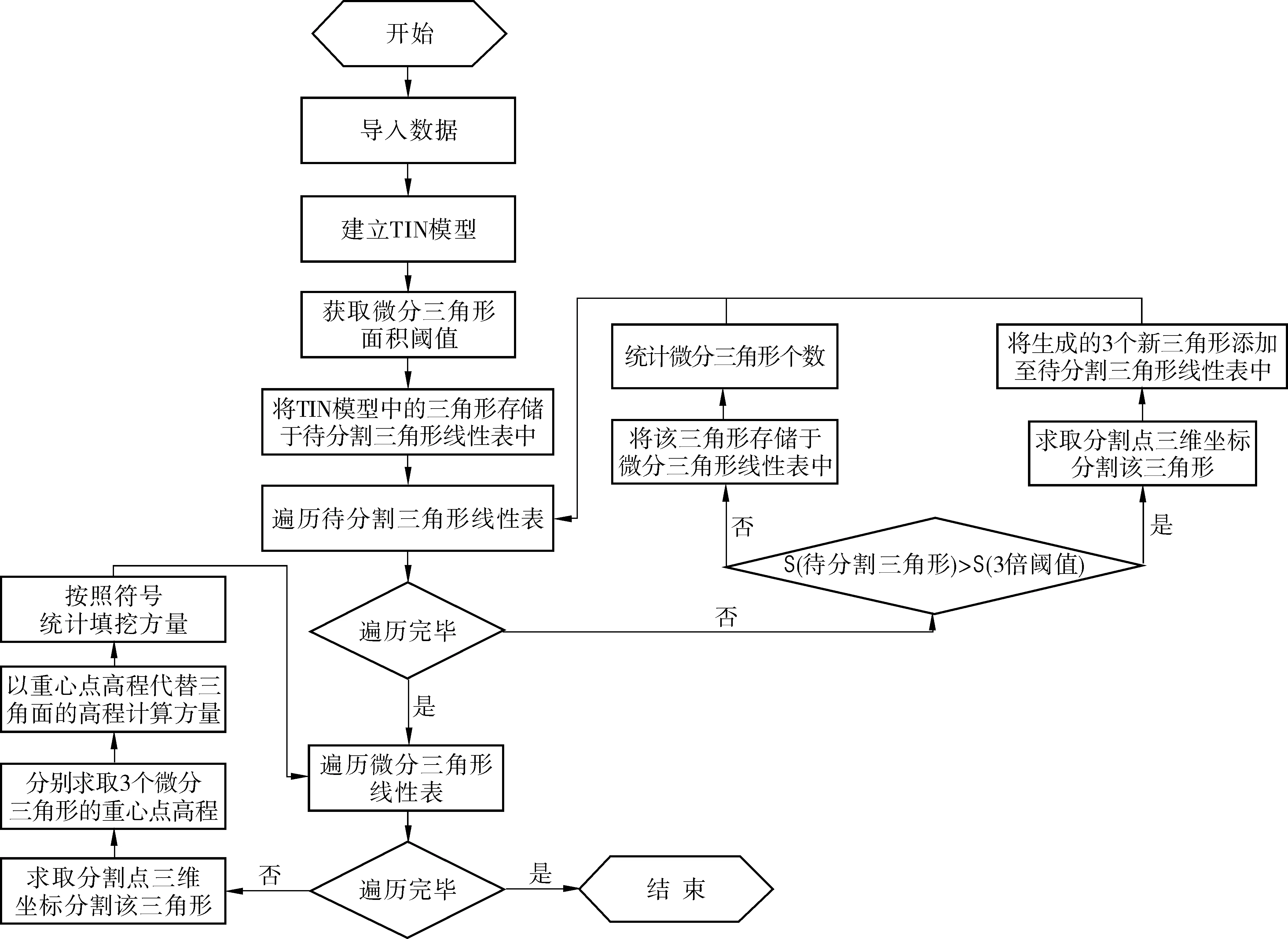
图2 基于TIN模型的三角形微分土石方计算流程Fig. 2 Flow chart of triangular differential earthwork calculation based on TIN model

2 实验与分析

基于三角形微分土石方计算理论，利用Visual Studio 2010平台，选择C#语言设计了一个微型土石方计算系统，能够实现TIN模型的构建、土方量的计算以及数据的输入输出，系统设计方案如图3。实验数据来源于重庆某场地平整土方工程，平场面积为71 913.1 m2，实测离散点138个。

2.1 算法分析

该算法与Grid法相似。当实验数据选取的阈值不断减小时，填挖方量趋于稳定。表1为实验数据在不同阈值下的填挖方量对比数据。由表1可知，在微分三角形的面积阈值分别1/60 m2和1/100 m2时，填挖方量仅相差1.4 m3，因此1/60 m2可认为是该项目的合适阈值。实际运算时，系统将依据不同阈值的结果对比数据，自动选择合适的阈值。

图3 基于TIN模型的三角形微分土石方计算系统设计方案Fig. 3 Design scheme of triangular differential earthwork computing system based on TIN model

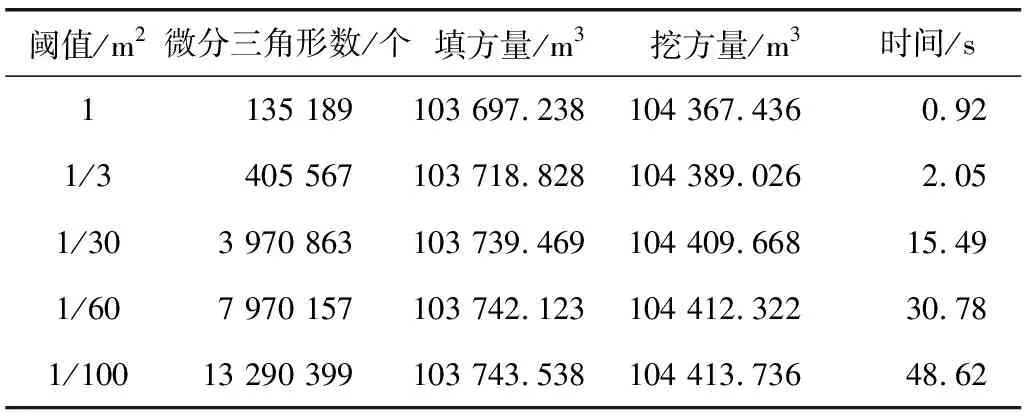
表1 实验数据选取不同阈值计算时填挖方量的变化Table 1 Variation of filling and excavation volume with differentthresholds selected in the experimental data

由表1可知，随着阈值的减小，微分三角形的个数大致呈线性增加，而且数量非常庞大。当阈值为1 m2时就能将初始的257个三角形微分为135 189个。选择较为合适的阈值(1/60 m2)进行计算时，微分三角形数量达到了797万个。而当结果真正稳定时，三角形数量突破了1 329万个。图4直观体现了不同阈值下微分三角形的数量变化。因此，大型土石方工程中运用三角形微分法对计算机的存储要求很高，而逐渐增加的微分三角形数量必然降低计算效率，表1中的计算时间直观体现了这一点。就算法而言，基于TIN模型的三角形微分土方石计算方法对计算机的性能要求较高，其发展与运用和计算机技术的发展有着直接的联系。

图4 同一三角形不同阈值的微分对比Fig. 4 Differential comparison of different thresholdsfor the same triangle

2.2 成果的对比分析

表2为各种土石方计算方法的结果对比数据。由表2可知，TIN法和三角形微分法的计算结果非常接近，而Grid法和这两者都相差较远。这反映了地形模拟对计算结果的影响远大于计算模型，也是一直以来众多土石方计算方法强调高精度的地形模拟而忽略计算模型的原因。但是如果要获得更高的精度，如利用土方量的变化进行地形沉降和滑坡的监测，对二者都应该有足够的重视。吴清海[11]介绍了一种利用两期土方量预测地面沉降的方法，其用泊松曲线对所得的土石方数据进行拟合并建立预测模型。此方法对土石方量的精度要求很高。

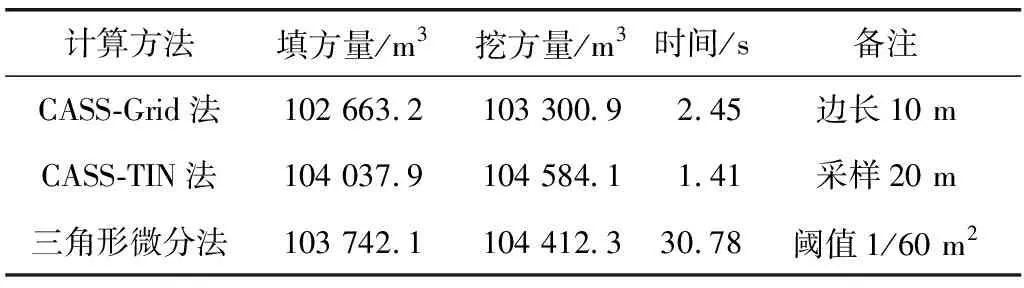
表2 各种土方计算方法结果对比Table 2 Comparison of the results of various earthworkcalculation methods

进一步分析表2可知，相对于CASS中的TIN法，三角形微分法填方量精度提高295.8 m3，挖方量提高了172.8 m3，计算时间多了29.37 s。由此可知，三角形微分法通过牺牲计算效率提高计算精度。就目前而言，一方面受限于计算机水平的发展，另一方面，在一般土石方工程中对填挖方量精度的要求不是很高，因此三角形微分法较难广泛应用于工程实际中。但是在一些利用两期土方量变化做动态监测的工程中，此方法具有运用前景。在利用土方量变化监测大坝和山区滑坡地带地形沉降、位移时，微小的精度提高就可能及早发现潜在的危险，对于保障人民的生命安全、减小经济损失具有重要的意义

3 结 语

基于TIN模型的三角形微分土石方计算方法，利用TIN构建地形模型，能够高精度地描述地形的细部结构。在计算模型方面引入了微分思想，将TIN模型中的每个初始三角形按照适当的阈值分割为微分三角形，在高程上以点代面进行计算，降低了计算模型的复杂度，减小了模型误差，提高了成果的精度。综合分析可知，此种方法通过牺牲计算效率提高精度，对计算机的存储和运算速率要求较高，因此在当下较难广泛应用于土石方工程中，只有在高精度的土石方监测项目中才具有实用意义。但随着计算机技术和交通土建行业的快速发展，此种方法具有很大的发展前景。