基于极限学习机的船舶航行行为预测

谢新连，陈紫薇，魏照坤，赵瑞嘉

(大连海事大学 物流研究院，辽宁 大连 116026)

0 引 言

随着海上交通监控技术及设备的发展，大多数船舶配备了船舶自动识别系统(automatic identification system, AIS)，来记录船舶的静态信息、动态信息及航次信息。这些信息可应用于交通流分析[1]、船舶异常行为检测[2,3]及船舶运动模式识别[4]。当船舶在海上航行时，尤其在交通密度较大、障碍物密集、通航环境复杂多变的海域，发生海上交通事故的风险增大。因此，基于船舶AIS数据，对船舶航行行为进行预测分析，不仅可以为海上交通事故预警提供重要技术支持，同时也对提高船舶监控效率、预防航行事故的发生具有重要意义。目前关于航迹预测的方法主要包括卡尔曼滤波、粒子滤波、灰色预测、神经网络等。其中基于卡尔曼滤波[5]、灰色预测[6]的船舶航迹预测模型，均需建立船舶运动状态方程才能实现对目标运动状态的预估。由于海况的动态性和不确定性导致了船舶运动的复杂性，建立实时船舶运动模型的难度较大，而神经网络本身具有较强的学习性，特别适用于样本数据规律未知、建模困难的情况。甄荣等[7]运用BP神经网络及AIS信息对船舶航行行为进行预测；U.SIMSIR[8]、D. ZISSIS[9]等利用人工神经网络对船舶航迹进行实时预测。

极限学习机(extreme learning machine，ELM)是由Huang Guangbin等[10]提出的基于单隐含层前馈神经网络(single-hidden layer feed-forward network，SLFN)的一种机器学习算法，多用于数据分类[11]、故障诊断[12]及预测[13,14]领域，在航迹预测领域应用较少。MAO Shangbo等[15]建立了可用于航迹学习、预测及数据挖掘领域AIS标准化数据库，并进行航迹预测试验，验证了极限学习机算法的有效性。笔者通过大量文献调查发现，以往研究的建模过程未考虑船舶航行状态发生改变引起预测误差波动较大的特殊情况，因此提出了基于AIS信息及极限学习机方法的船舶航行行为预测模型，在文献[7]对船舶航行行为预测研究的基础上，通过对不同航行状态下的船舶采取自动调整采样周期的方法提高对转向及变速过程中的船舶航行行为预测精度，实现船舶航行行为的实时预测。

1 基于AIS信息的船舶航行行为

AIS信息分为静态信息、动态信息及航次信息。静态信息包括船名、船长、船宽、船舶类型、呼号、船舶海上移动业务识别码(maritime mobile service identity，MMSI)等；动态信息包括船舶经纬度坐标、航速、航向等；航次信息包括船舶吃水、货物类型、航行始发港、目的港及预计到达时间[8]。

通常狭义上的船舶行为是指船舶在驾驶人员操纵下以船舶航行与避让为主要目的的行动方式与规律[16]。顾名思义，船舶航行行为主要体现在船舶的一系列航行状态随时间的变化上。每个航行状态包括动态船位、航速、航向等动态属性，主要体现在AIS动态数据中的经度(LON)、纬度(LAT)、对地航速(SOG)、对地航向(COG)4个指标上，其更新频率根据船舶航行状态及AIS设备类型而定。A类AIS设备动态信息的发送速率要求如表1，B类AIS发送速率的要求则低于A类。表1中，航速为0 kn且不转向的船舶状态代表锚泊。AIS信息的及时更新，确保了对船舶航行过程的实时监控，有助于海上监控系统的发展及事故调查研究。

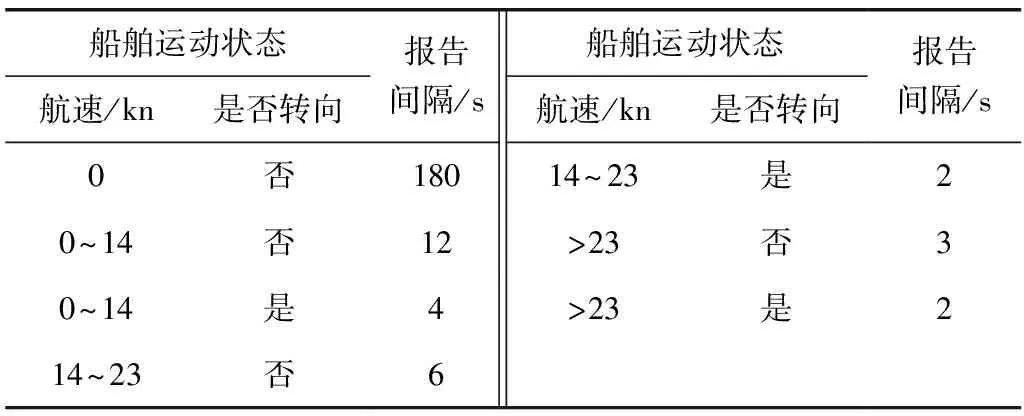
表1 A类AIS设备信息发送速率Table 1 Class A AIS device information transmission rate

2 基于极限学习机的船舶航行行为预测模型

2.1 网络结构

图1 基于ELM的船舶航行行为预测模型Fig. 1 Prediction model of ship navigation behavior based on ELM

在进行预测前，需要对该网络模型进行训练，其训练过程如下：

1)给定训练样本集:

{S,T}={(Sj,Tj)|j=1,2,…,u}

(1)

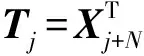
2)设置激活函数G(·)及隐含层节点数nh。随机生成隐含层输入权值wi及隐含层偏置向量bi，计算隐含层输出矩阵H：

H(w1,…,wnh,b1,…,bnh,S1,…,Su)=

(2)

3)通过求解式(3)的最小二乘解，计算输出权值β：

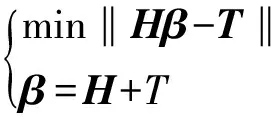
(3)

β具有使网络训练误差最小、泛化性能最优的特性。则该极限学习机预测模型在数学上可表示为：

(4)

2.2 样本时间设定

当船舶在狭窄水域或弯曲航道航行时，难免会发生转向或变速行为，此时预测时间间隔过长或固定不变会影响预测结果的精确性、适应性及有效性[17]。因此，当船舶处于转向或变速航段时，为准确学习船舶的航行行为，需要根据船舶航行特点合理调整采样时间间隔，合理训练学习网络，使其适应船舶航行特征的改变。例如，初始训练网络的航迹采样周期为t1；船舶t时刻与上一时刻的航向变化ΔC>C0，或航速变化ΔV>V0时，此时认为船舶处于转向或变速航段，则将采样周期及预测时间间隔Δt设置为t2。因此，预测模型的采样时间间隔与预测时间间隔可表示为：

(5)

2.3 基于ELM的船舶航行行为预测流程

基于ELM算法进行船舶航行行为预测的主要框架是将海域内船舶近期航迹数据作为训练集，通过将网络实际输出与期望输出对比训练网络，建立船舶历史航迹与未来航迹的映射关系，再代入预测样本进行预测。因此，在预测前需要对提取的航迹数据进行分组，每组数据的个数由训练样本及预测样本总的时间长度而定。具体的分组及预测流程如图2。

图2 基于ELM算法的航迹预测流程Fig. 2 Navigation track prediction process based on ELM algorithm

在设置每组数据的采样时间间隔时应注意，当前一组数据采样及预测时间间隔Δt=t1时，每当提取1条航迹数据，将其和前一条航迹数据航向及航速的变化与设定的阈值进行判断，若航速或航向变化小于阈值，则确定该组数据的Δt=t1；若大于阈值则设置Δt=t2。当前一组数据采样及预测时间间隔Δt=t2时，若提取的航迹数据的航速或航向变化小于阈值，则需要反推一组Δt=t1的航迹数据，并对组内其他航迹再次进行航速及航向变化的阈值判断；若皆小于阈值则证明训练集具有与预测集相近的特性，即可确定该组数据Δt=t1；若大于阈值，则设置Δt=t2。依次类推，可提取K0组船舶航行航迹数据进行船舶航行行为预测，K0为预先设置的预测序列个数。

在整个预测过程中，每组数据组成的样本数量均为u+m，虽然其随着AIS数据的实时更新，从当前时间点开始会依据速度及转向判断确定采样周期，重新提取数据、更新训练集及预测样本，但始终将当前t时刻的船舶行为特征值Xt作为最新一组数据第u个样本的期望输出Tu，并以{(S1,T1),(S2,T2),…,(Su,Tu)}作为训练集训练网络，将yi作为预测样本的输入进行预测，确保了训练样本集是距离预测样本最近的u个样本，从而实现模型的在线训练及实时预测。

3 仿真实验

3.1 参数设置

仿真实验中，N=6，即用前6个时刻的船舶航行行为特征值预测下一时刻的船舶航行行为。对应的输入层节点数为24个，输出层节点数为4个，隐含层激活函数为sigmod函数。为方便进行后面误差分析及算法对比试验，笔者仅进行单步预测，即m=1。通过反复试算，结果如图3。

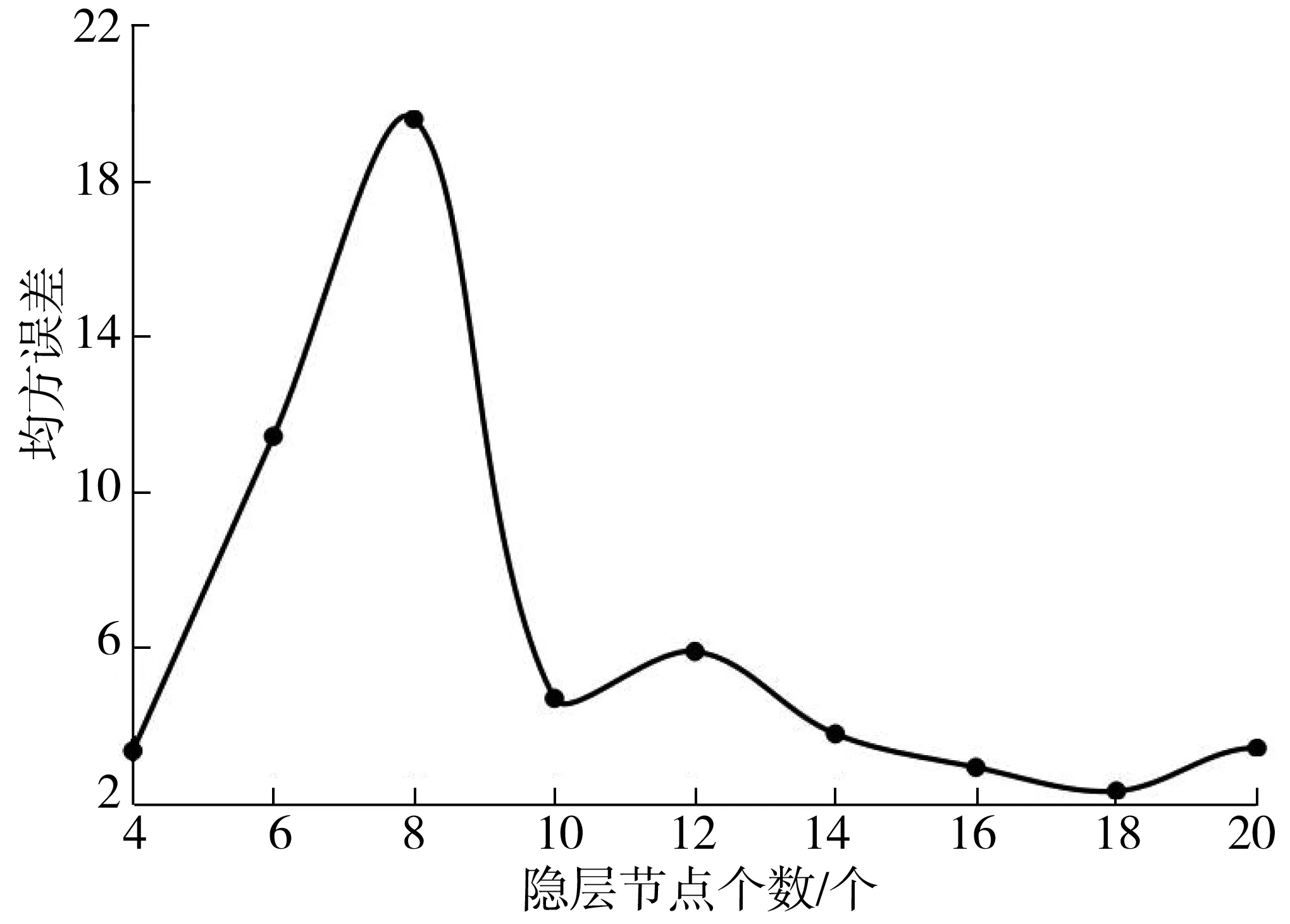
图3 不同隐层节点数的网络均方误差对比Fig. 3 Comparison of network mean square errors of different numberof hidden layer nodes

隐含层节点个数设置为18时，4个指标总体均方误差(MSE)最小，预测次数K0依预测时间而定。图4为算法在不同数量训练样本时的预测误差。当样本采样间隔设置为1 min时，可以看到训练样本个数为8个时误差最小，因此笔者将训练样本个数设置为8个，每组数据个数为15。由于船舶在实际航行中存在较大惯性和一定的操作反应时间，因此将动态数据的采样和预测时间间隔确定为5 min，即t1=5 min，将船舶转向及变速阈值分别设置为10°、0.3 kn，采样与预测时间间隔t2=10 s。

3.2 数据处理

以琼州海峡某日多艘船舶的AIS数据作为实验数据进行船舶航行行为预测实验。由于船舶AIS设备发射动态数据的频率取决于船舶航行速度，该船舶的航速区间为0.1～16.1 kn，此时AIS动态数据的实际发射频率为5 s～3 min不等。为保证预测时间间隔的一致性，对于某时间点丢失、未记录的航迹数据采用线性插值法进行填充，并将提取后的数据进行分组及样本整理。每组数据可分为8个样本，取前7个样本作为训练样本，训练神经网络，第8个样本作为预测样本进行预测。

3.3 仿真结果及分析

为验证模型的通用性，选取琼州海峡内5条不同类型的航迹进行仿真实验，包括直线航迹及曲线航迹，预测的均方根误差(RMSE)均处于较低水平，结果如表2。

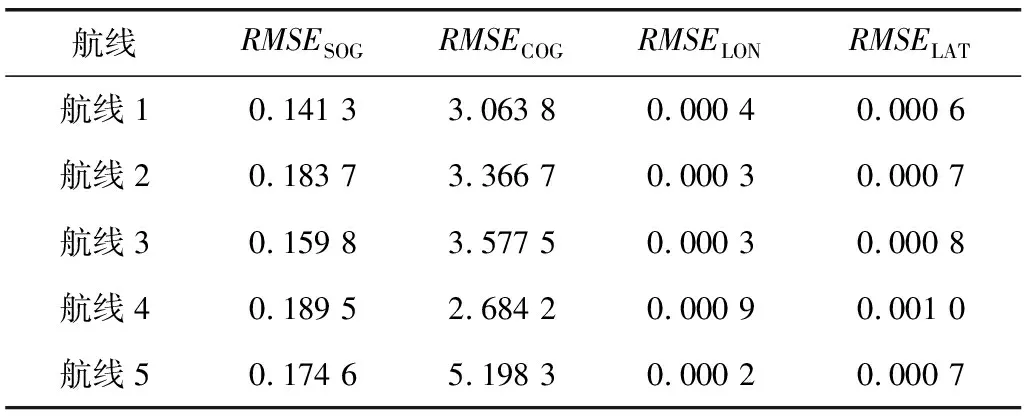
表2 基于ELM预测模型的5条航迹预测误差Table 2 Prediction error of 5 tracks based on ELM prediction model

取预测周期最长且包括转向及变速航段的航迹1为例进行具体误差分析。在该航迹实验中对该船进行为期16 h的跟踪预测，此时K0=200，海图上显示的船舶实际航迹及预测航迹如图5，训练及测试时间共计46.9 s。由图5可见，基于ELM的预测航迹与实际航迹趋势相同，近乎重合，预测效果较好。

为定量表达二者之间的误差，分别对预测经度、纬度进行误差分析，结果如图6。经度误差可控制在0.003°以内，大部分误差在0°～0.001°区间，纬度误差最大为0.003°，其误差主要分布在0°～0.001°区间。图7为航速预测及航速预测误差结果。由图7可知，预测航速的变化趋势与实际航速变化趋势基本一致，预测误差在1 kn以内。图8为航向预测及航向预测误差结果。由图8可知，航向预测误差范围为0°～27°，主要分布在10°以内。

由图7、图8可知，从K=100到K=150，航速由16 kn减速到13.3 kn，对地航向从269.41°增加到319.78°，此时船舶正处于转向及变速过程中。从误差图中可知，此区间内船舶航行行为预测精度并未受到船舶变速及转向行为的影响而增大。

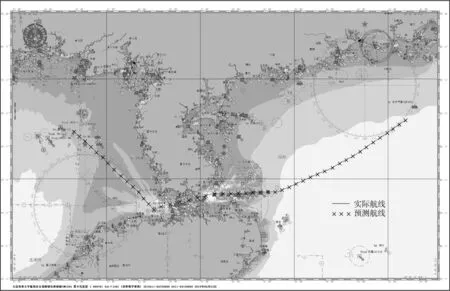
图5 实际航迹和预测航迹Fig. 5 Actual track and prediction track

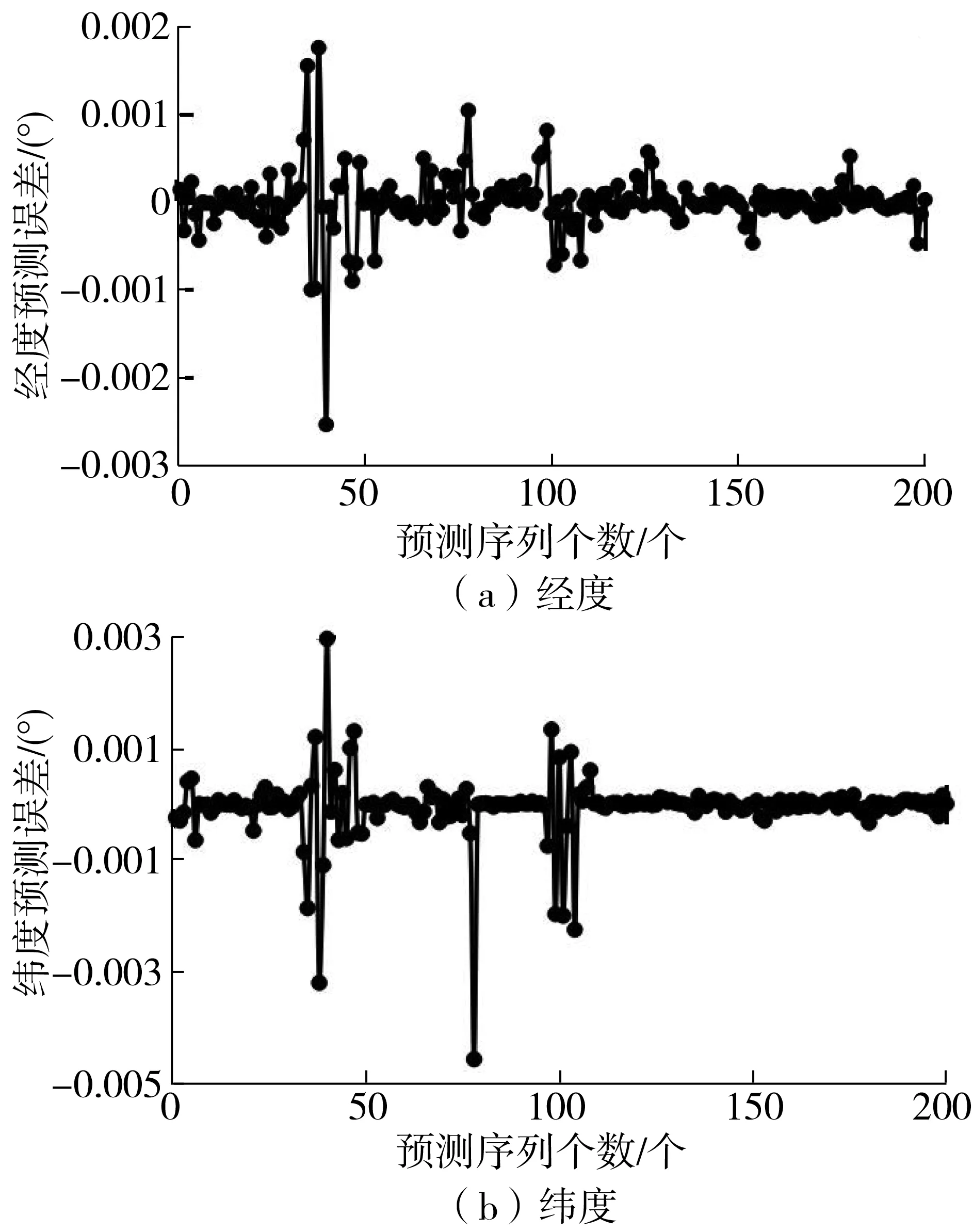
图6 预测误差Fig. 6 Prediction error

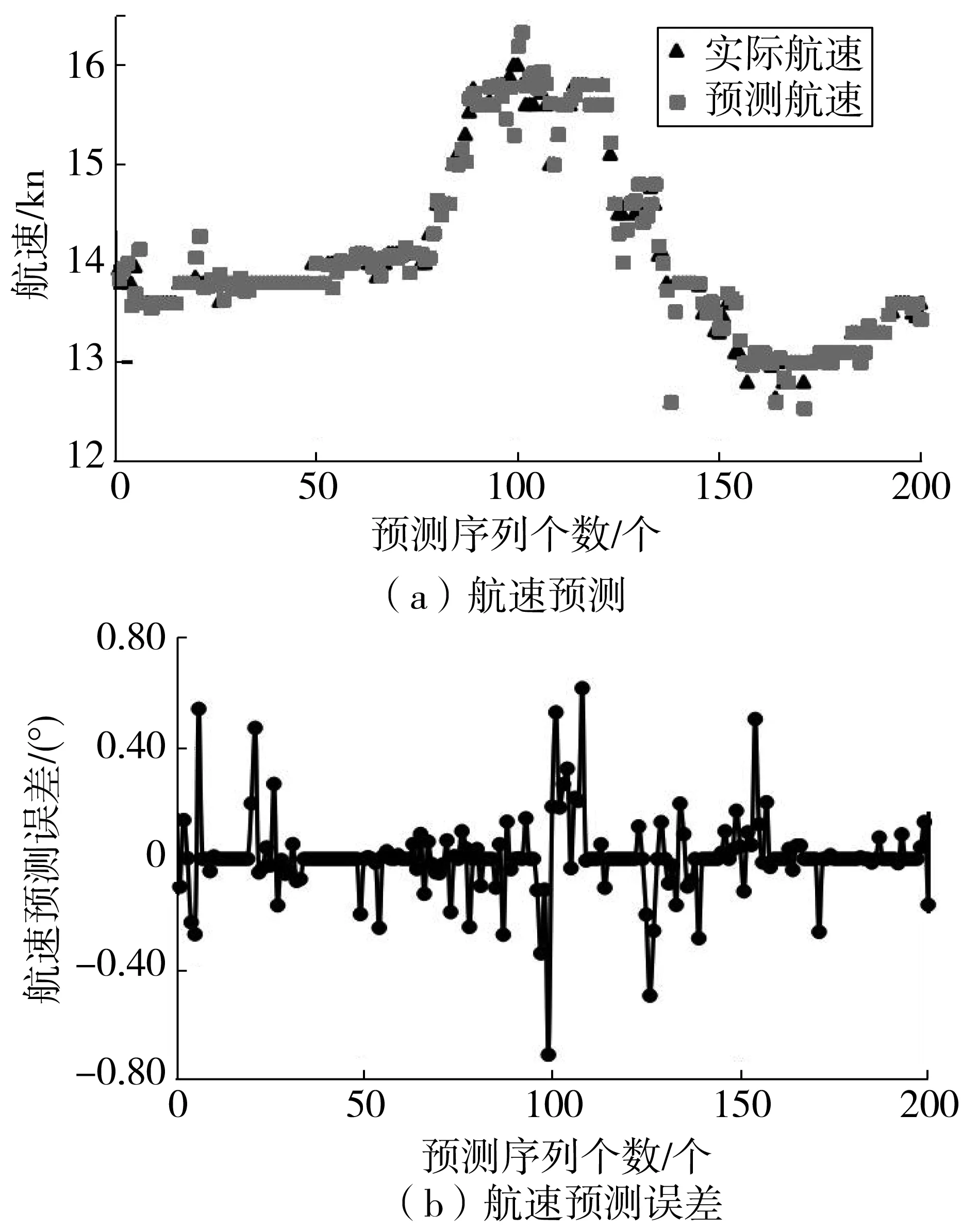
图7 航速预测和航速预测误差Fig. 7 Speed prediction and speed prediction error

图8 航向预测和航向预测误差Fig. 8 Course prediction and course prediction error

3.4 算法对比

在对比实验中，采取文献[7]中的BP神经网络模型及文献[6]中的灰色预测模型，对5条航迹均进行了船舶航行行为预测，其预测误差均大于ELM预测模型的预测误差。以航线1为例，对3种方法的预测性能进行多方面对比及显著性检验。表3给出了极限学习机、BP神经网络及灰色预测模型在平均绝对误差、最大绝对误差、均方根误差及平均绝对百分比误差(MAPE)评价方面的对比数据。

表3 ELM与BP神经网络、灰色预测性能对比Table 3 Performance comparison between ELM, BP neural networkand grey prediction algorithm

由表3可以看出，基于极限学习机的船舶航行行为预测模型在航速、航向、经度、纬度方面的预测精度皆优于其他方法，这是因为可调节的采样间隔提高了训练样本的有效性，从而进一步提高预测精度。除此之外，BP神经网络的训练及学习时间为124.43 s，与其相比，ELM预测模型的训练及测试时间减少了77.53 s。

借助SPSS 14.0软件，对ELM与BP神经网络模型、灰色预测模型的船舶航行行为预测误差分别进行曼-惠特尼U检验，检验结果如表4。除BP模型的航速预测误差外，其他指标的P值皆小于5%显著水平，说明3种方法的船舶航行行为预测误差总体差异在统计上显著，且从误差均值可以看出ELM算法的预测性能明显优于BP模型及灰色预测。

表4 ELM与BP神经网络、灰色预测算法的误差显著性分析Table 4 Error significance analysis of ELM, BP neural network andgrey prediction algorithm

4 结 论

基于神经网络突出的自学习能力，提出了基于极限学习机算法的船舶航行行为预测模型。该模型针对在以往研究中船舶在转向及变速航段预测性能较差的问题，设计了根据船舶航行状态自动调整采样周期的判断条件，实现船舶航行行为的在线学习及预测。在仿真实验中对琼州海峡水域内5条典型航线进行了跟踪预测，并以其中1条航线为例，与传统BP神经网络模型及灰色预测模型进行预测性能分析及显著性检验。实验结果表明：基于极限学习机的船舶航行行为预测模型具有较优的预测性能及时间优势。该研究在一定程度上改善了传统预测模型在航行状态变化前后(变速或转向)预测误差较大的状况，可适用于在弯曲河道中航行船舶的行为预测，同时对提高监控效率，保障航行安全具有一定的理论及现实意义。