基于递推最小二乘法的转向系统参数辨识

李 伟，王洪民，唐 峥

(重庆交通大学 机电与车辆工程学院，重庆 400074)

0 引 言

转向系统是控制汽车按指定路线和方向行驶的重要装置，精确的物理参数在对建立车辆系统动态数学模型和分析中起着至关重要的作用[1]。针对系统的参数辨识，比较主流的辨识方法有模型自适应辨识算法[2]、最小二乘法[3-4]、扩展卡尔曼滤波法[5-6]、遗传算法[7]、扫频测试等。其中扩展卡尔曼滤波法的P、Q矩阵很难确定，而且与系统状态密切相关；遗传算法对待估参数初值要求较高；扫频测试需要用不同的频率去激励系统，再用最小二乘法求得闭环系统的幅频特性与相频特性，最后利用MTLAB的INVFREQS函数进行拟合，这种算法采集到的数据不仅不多，而且还要进行两次拟合，会造成辨识出的参数结果精度不高；加之遗传算法和扫频测试也不能做到参数在线实时估计。宗长富等[8]采用最小二乘法与遗传算法相结合的方法以TruckSim数据为基础离线辨识出了商用车三自由度模型的前轴侧偏刚度、后轴侧偏刚度、侧倾阻尼和侧倾刚度4个关键参数，并绘制出辨识出参数的MAP图，代入数学模型进行仿真验证。结果表明：该方法能较准确辨识出系统模型的关键参数，关键参数MAP图能实时准确表征车辆的实时动态特性，为商用车参数估计和稳定性控制奠定了良好基础。李凌阳[9]对车辆悬架系统的进行参数辨识研究，分别采用对数衰减法、频域法和面积法来辨识悬架系统的阻尼比，并利用系统模型辨识出车辆的簧上和簧下质量，对于研究悬架主动控制策略具有非常重要的意义。

首先利用MATLAB进行递推最小二乘法仿真，结果表明，该方法能够快速有效准确地估计出系统参数；然后MicroAutoBox发出PWM波控制P-EPS驱动版中“H”桥中4个功率晶体管的通断，利用博世传感器采集转向系统中方向盘的转角，系统的输入电流由驱动板采集，根据采集的电流和转角编写递推最小二乘法，对未知转向系统的有关参数进行在线估计。

1 递推最小二乘法原理

考虑如下受控自回归(controlled autoregressive,CAR)模型：

A(z-1)y(k)=B(z-1)u(k-h)+ξ(k)

(1)

式中：u(k)为白噪声；ξ(k)和y(k)分别为系统的输入输出；h为已知数，且

式中：na、nb为结构参数并已知。

参数估计的任务是根据可测量的输入和输出，确定如下na+nb+1个参数：

a1,a2,…ana;b0,b1,b2,…,bnb

对式(1)写成如下最小二乘法格式：

y(k)=-a1y(k-1)-…-anay(k-na)+b0u(k-d)+…+bnbu(k-d-nb)+ξ(k)=φT(k)θ+ξ(k)

式中：φ(k)为数据向量；θ为待估参数向量，且：

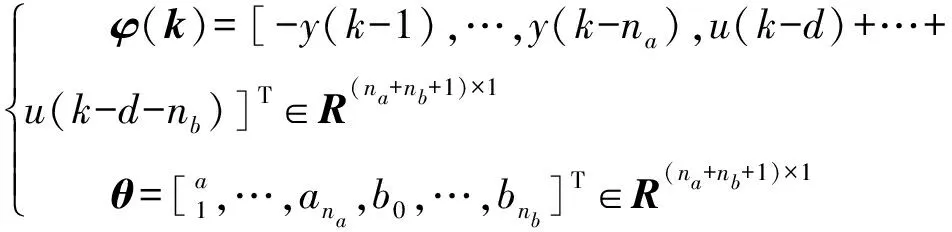
(2)

式中：

设k时刻最小二乘估计为

(3)

式中：

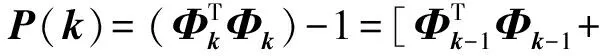
φ(k)φT(k)]-1=[P-1(k-1)+φ(k)φT(k)]-1

则:P-1(k)=P-1(k-1)+φ(k)φT(k)

(4)

(5)

则由式(4)和式(5)可得：

于是k时刻的最小二乘估计可表示为

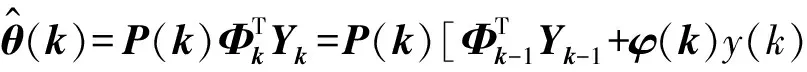
(6)

式中：

K(k)=P(k)φ(k)

(7)

根据矩阵求逆原理，设A、(A+BC)和(I+CA-1B)均为非奇异方阵，则

(A+BC)-1=A-1-A-1B(I+CA-1B)-1CA-1

(8)

令A=P-1(k-1)、B=φ(k)、C=φT(k)，得

P(k)=P(k-1)-P(k-1)φ(k)[1+φ(k)P(k-1)φ(k)]-1φT(k)P(k-1)

(9)

将式(9)带入式(7)，可得：

K(k)=P(k-1)φ(k)-

(10)

由式(9)和式(10)可得：

P(k)=[I-K(k)φT(k)]P(k-1)

(11)

(12)

2 输入信号的选择

如果建立的系统数学模型结构选择正确，则模型参数辨识的精度好坏将直接依赖于系统输入信号，因此选用合理的输入信号是保证能否获得理想的辨识结果的关键因素之一。通过理论分析表明，选用白噪声作为辨识输入信号可以获得较好的辨识结果，但这在工程上几乎不易实现，因为实际工业设备不可能按白噪声的变化规律动作。采用近似白噪声的逆M序列代替白噪声信号。

2.1 M序列定义

设有一个无限长的二元序列x1,x2, …,xp,xp+1，各元素间存在下列关系：

xi=a1xi-1⊕a2xi-2⊕…⊕apxi-p

式中：i=p+1,p+2,…；系数a1,a2,…,ap-1取值为0或1；系数ap总为1；⊕为异或运算符。

只要适当选择系数a1,a2,…,ap-1，就可以使序列以(2p-1)bit的最长周期循环，这种具有最长循环周期的二元序列称为M序列。

M序列它具有近似白噪声的性质，是一种很好的系统辨识输入信号。其主要性质有：

1)均衡性。在M序列一个周期中，1的个数比0的个数要多1位，这表明该序列平均值很小。

2)M序列有良好的自相关性。

3)M序列发生器中移位寄存器的各种状态，除了全0状态外，其他状态只在M序列中出现一次。

2.2 逆M序列

由谱分析表明，M序列通常含有直流成分，可能会造成辨识系统的“净扰动”，这通常是我们不希望的。而逆M序列可以克服这一缺点，是一种比M序列更为理想的伪随机码序列。

设M(k)是周期为Npbit、元素取值为0或1的M序列，S(k)是周期为2bit、元素依次取值为0或1的方波序列，将这两个序列按位进行异或运算，得到的复合序列就是周期为bit、元素取值为0或1的逆M序列，记作{IM(k)}，即有：

{IM(k)}={M(k)}⊕{S(k)}

将上述逆M序列的逻辑值“0”或“1”分别换为-1或1，此时逆M序列均值为0。

虽然逆M序列是M序列与方波序列简单复合的结果，但其性质却优于M序列，使它在辨识领域中有着更加广泛的应用。

3 仿真与分析

已知有如下三阶系统的传递函数模型：

(13)

需要辨识的系统参数有2、50、100、10。取采样时间为0.1 s，采用后向差分法即：

(14)

由式(13)和式(14)可以得出：

(15)

将式(15)写成CAR形式：

(16)

这里模拟采集数据时有白噪声的误差干扰，因此将式(16)修正为

(17)

式中：ξ(k)为方差为1的白噪声；u(k)为取值为1，-1的逆M序列。

这里只要辨识出-39/18、16/9、-5/9、1/180就可以由式(15)反推出三阶系统中的各个参数。式(17)中参数辨识的精度可以反映式(13)中参数的精度。对式(17)编写最小递推最小二乘算法，其辨识结果如表1。

表1 参数辨识结果Table 1 Parameter identification results

从表1可以看出，前面3个参数的估计相对误差都在0.2%以内，而最后一个参数由于本身数值特别小，但通过递推最小二乘法可以准确估算到千分位，相对误差也控制在4%以内。并且随着所取数据的不断增大，系统辨识的结果也会随之改善。这就是递推最小二乘法的一个优势，可以根据不断更新的数据，对前面所辨识的结果进行改善，使得辨识的结果更加接近真实值。

本次仿真采集10 000组数据，如图1，可以观测各个参数辨识的变化曲线，其中a1为-39/18的估计曲线、a2为16/19的估计曲线、a3为-5/9的估计曲线、b0为1/180的估计曲线、k为仿真步长。

综上可以得出，递推最小二乘法可以准确辨识出参数，辨识结果也比较理想。

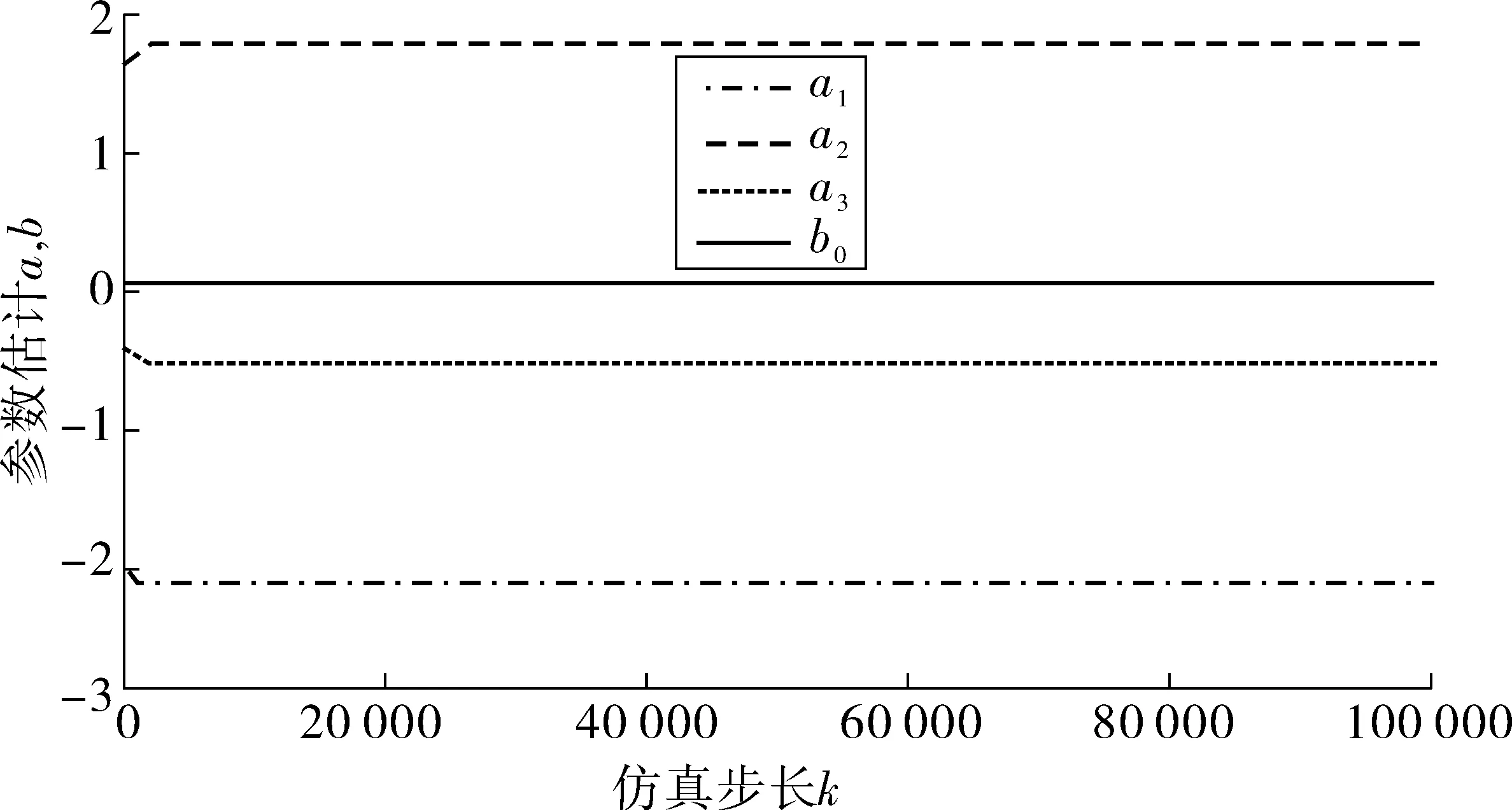
图1 各估计参数的实时变化Fig. 1 Real-time changes of the estimated parameters

4 应用与推广

转向系统模型如式(18)：

(18)

式中：J是等效到小齿轮上的转动惯量；b是等效到小齿轮上的阻尼；km是等效到小齿轮上的刚度；kI是力矩系数；im是小齿轮传动比；θ是方向盘转角；i(t)是电机电流。

对式(14)进行拉普拉斯变换可得到转向系统的传递函数为

(19)

这里采用后向差分法对式(15)进行离散化处理，取采样时间为0.1 s，则有：

其中：

(20)

从而可以得到离散系统的表达式为

(21)

这里给电机输入电压为±4.8 V的逆M序列，i(k)为系统的输入电流由驱动板采集，输出转角用博世传感器进行采集。实验基本框图如图2。

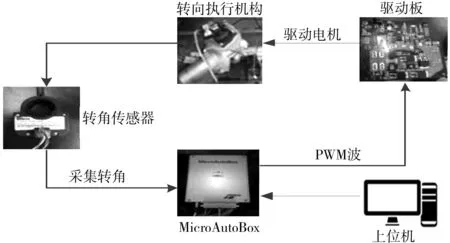
图2 实验基本框图Fig. 2 Basic block diagram of the experiment

在MATLAB/Simulink软件搭建电机驱动模型，并由dspace提供程序编译环境，通过MicroAutoBox硬件输出PWM波来控制驱动板中4个功率晶体管的通断，来实现电机的调速功能，利用博世转角传感器对方向盘的转角进行采集，由于该角度传感器只接受ID为550 h的十六进制CAN报文，需要对采集到的数据进行破译，这里可以利用dspace自带的ControlDesk软件用来记录数据，此时记录的数据是十进制的，不用在破译。实验平台如图3。

图3 实验平台Fig. 3 Experimental platform

运行模型并用ControlDesk记录博世角度传感器采集的转角数据，根据采集的输出转角及输入电流，编写递推最小二乘法算法，实验过程时，各参数的变化收敛如图4，辨识结果为表2。

通过图4可以实时在线观测各参数的变化过程，也可以看出，递推最小二乘法的收敛速度比较快，在k=500时，各个参数已趋于稳定。

式(18)中小齿轮传动比im=18.75，用电机型式试验自动测试系统测得电机的力矩系数kI=0.056 3，因此将参数估计值带入式(20)可以解出转向系统参数如表3。

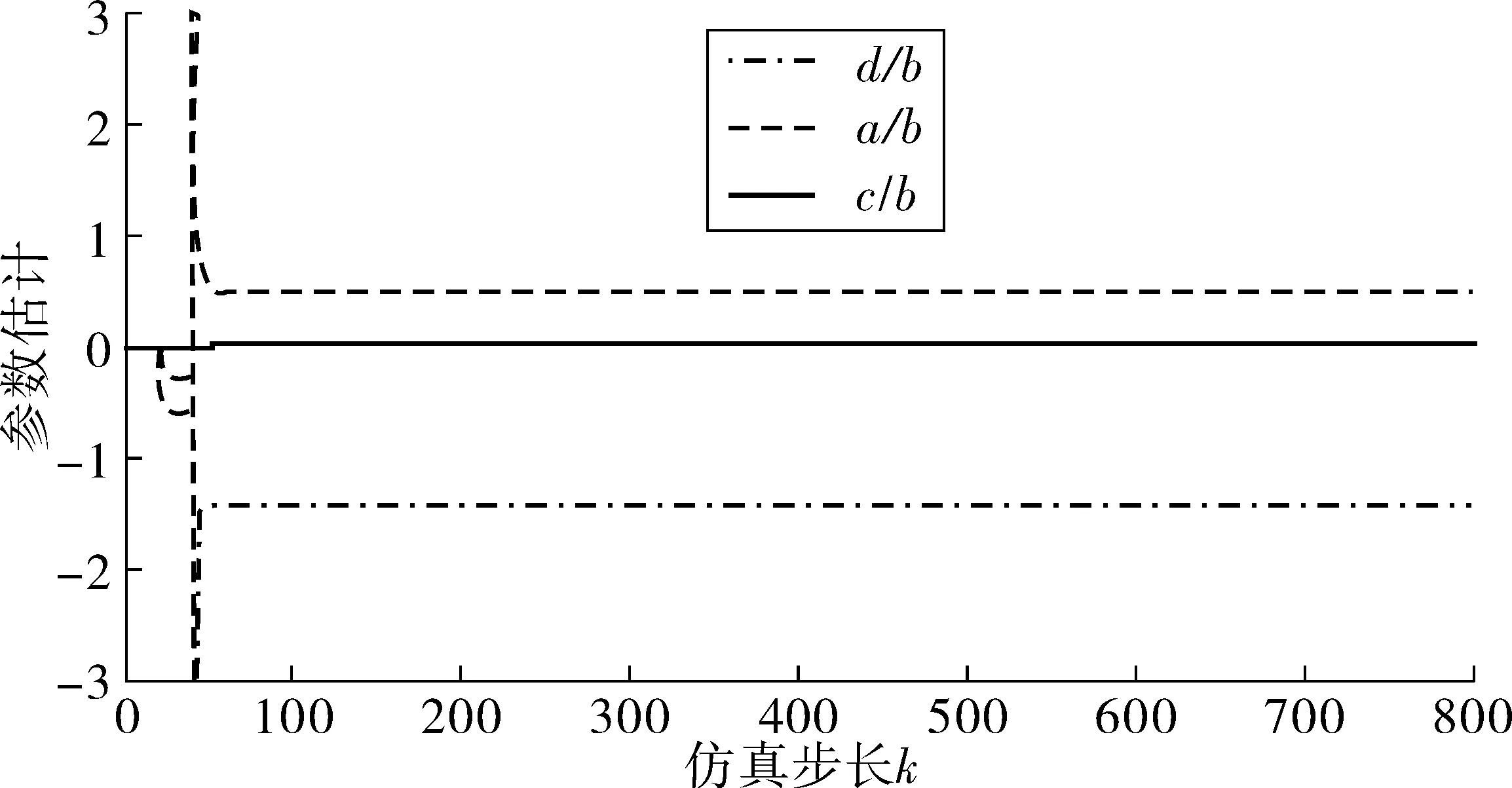
图4 各参数的变化收敛过程Fig. 4 Convergence process of each parameter change

参数c/bd/ba/b参数估计值-1.425 90.540 20.044 1

表3 转向系统参数Table 3 Steering system parameters

因此转向系统的模型为

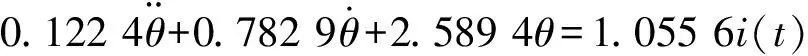
(22)

对辨识的参数进行验证，验证结果如图5。

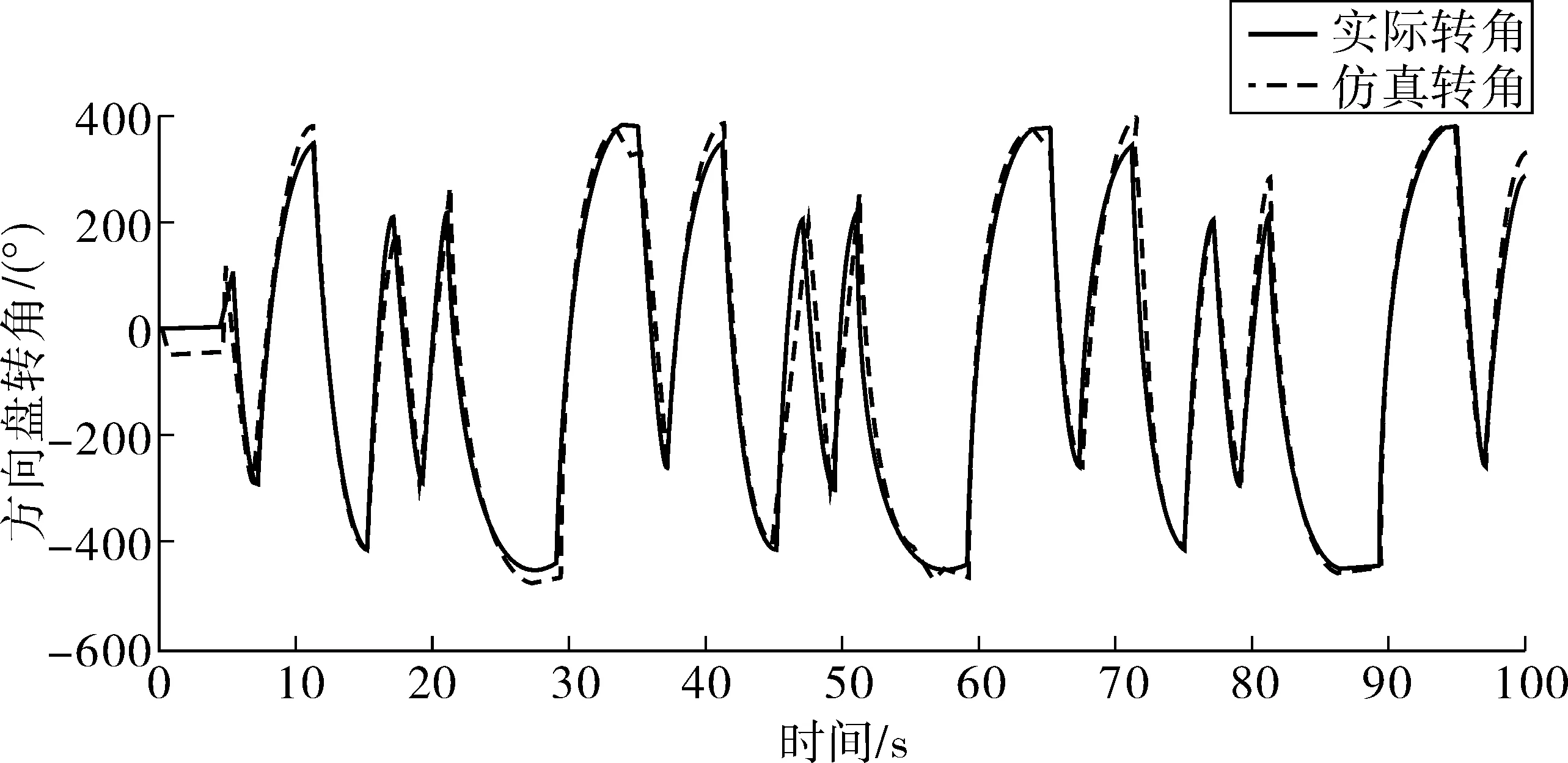
图5 实际转角与仿真转角的对比Fig. 5 Comparison of actual corner and simulated corner

通过图5可以看出，传感器采集的实际转角与通过辨识出来的参数的转向系统模型仿真出的转角非常相近，对辨识出的参数结果满意。

5 结 语

根据表1仿真的结果表明，递推最小二乘法可以快速准确的识别参数，参数辨识的精度也令人满意。且在很多自适应控制系统中，被控对象通常都在不断提供新的输入输出数据，而且希望能够利用这些新信息来继续改善参数估计的精度，递推最小二乘法的在线实时估计能够很好的解决这个问题。

笔者还将该算法应用到了汽车转向系统上，辨识出了转向系统的等效转动惯量、等效阻尼系数、等效刚度，并对辨识出的参数进行了验证，通过图5可以看出验证结果理想。此理论对未知系统参数辨识的研究具有重大意义。