基于分时定价理论的地铁票价优化研究

王 林,李日伟,鲁寒宇,杨雨婷

(武汉理工大学 交通学院， 湖北 武汉 430063)

0 引 言

如今，随着城市化的推进，城市人口日益增长，造成公共交通高峰期出行乘客过多，平峰期出行人数偏少，出行客流较为集中，全天客流不均衡系数偏大的问题，不仅会导致公共交通服务质量下降，也会增加安全风险与维护费用。作为城市公共交通的重要分担者，地铁同样存在此问题，且问题表现较为突出。就历史数据分析来看，乘客对地铁票价的敏感性较强，因此，通过对地铁进行分时间段的票价优化，达到调整弹性系数较大的乘客出行时间与出行方式，分散出行客流，缓减客流不平衡矛盾的思想是可行的。

分时定价理论是指，从“削峰填谷”的思想出发，根据运营时段不同制定不同的价格，利用乘客对公共交通价格的敏感性，引导乘客的出行时段与出行方式，是一种平衡不同时段出行客流量的有效方法。目前，有许多学者对此问题进行了研究讨论。S. R. JARA-DIAZ[1]于1986年首先运用分时定价理论，对圣地亚哥地铁系统进行分时定价，并通过建立非集计需求模型和使用多产出成本函数计算出最优的价格，结果表明了分时定价在圣地亚哥地铁系统的可适用性；R. BIANCHI[2]等通过建立乘客行为模型，借助SP调査法对圣地亚哥地铁实施分时定价政策前票价对早晚高峰客流的影响进行调査，来预测票价和舒适性改变后乘客出行时间的变化，并得出了Probit模型对于现实中分时定价政策实施后客流量变化的巧合效果更优，同时对分时定价在圣地亚哥地铁实施给予肯定；王倩[3]构建了伯特兰均衡模型和双层规划定价模型，基于具体算例提出了在城市轨道交通运营的不同时期应根据实际情况制定不同票价的方案；李艳杰[4]利用计量经济学方法分别以客流量与平均运距为变量进行 OLS 回归，得出变量对拉姆齐定价的影响情况，同时得出深圳地铁的拉姆齐定价与高峰定价；宋庆梅[5]建立巢式 Logit 模型，以杭州地铁为例进行验证，得出时间差别定价能有效平衡客流时空分布不均衡现象，但可能会减少地铁票务收入的结论；王静[6]从收益管理和拥挤定价出发，应用 SP 问卷调研和 Weka 分析，发现乘客出行影响规则，并通过分类预测方法确定了广州地铁的低峰降价策略；程高[7]基于博弈论构建了非对称信息下的公交定价模型，以武汉地铁为例，以社会效益最大化为目标计算出了4元的最优票价；刘涛等[8]通过价格敏感度模型和拥挤容忍度模型，验证了地铁分时定价的必要性；陈花[9]以定性分析为主，论述了地铁分时定价对于乘客出行选择的影响。上述研究从收益定价或时间差别定价角度取得了诸多研究成果，但总的来看，分时定价的研究以定性分析为主，少数的定量分析则采用平峰打折或高峰涨价的策略，很少采用数学模型进行整体优化。基于此，笔者参考诸克军等[10]关于天然气工业分时定价的策略，选用弹性系数法，对地铁各时段重新定价，在保证地铁社会公共性发挥的同时，缩小最大客流差，保障地铁的安全运营。

1 价格弹性模型

价格弹性可以充分反映供求与价格之间依存关系，准确反映乘客对票价的敏感性。就地铁公交等公共交通而言，经历史数据分析[11]，其对票价的弹性较大，因此，对地铁进行分时定价后，乘客的需求也会发生相应变化，且乘客对某时段的地铁需求量不仅与该时段地铁票价有关，也与其他时段地铁票价有关，即同时存在自弹性和交叉弹性。价格弹性的一般形式如式(1)：

(1)

笔者根据价格弹性的一般形式，分析自弹性和交叉弹性。

1.1 自弹性系数

自弹性系数公式如式(2)：

(2)

自弹性系数用于衡量某一时段的价格弹性，即第i个时段的价格变化。自弹性系数只影响第i个时段的需求变化，而不影响第j(i≠j)个时段的需求变化，亦即客流量在同一时段的不同交通方式重新分担。例如，大部分上学、上班等刚性需求。

1.2 交叉弹性系数

交叉弹性系数公式如式(3)：

(3)

交叉弹性系数为其他时段票价变化对某一时段的客流需求影响，即第j个时段的价格变化影响第i(i≠j)个时段的需求变化，亦即客流量转移至其他时段。例如，出行等非刚性需求。

2 用户需求响应负荷模型

需求响应(demand response，DR)在现有研究中主要用于电力需求管理，是指电力用户根据供电部门制定的电价信息和激励信息来调整自己的用电计划,通过用电设备技术改进或采用控制手段对运行方式进行调整以改变其用电负荷特性曲线,在用户满意度和用户生产工艺约束条件下,使用户电费支出最小化[12]。参照此定义，可将地铁需求响应定义为：当地铁票价发生变化时，乘客接收到票价变化信号后，改变其出行行为，从而减少或者推移某时段出行负荷，在最大客流差缩小的约束下，保障乘客的出行效益。

参考文献[13-14]与文献[10]，提出关于地铁乘客的用户响应负荷模型，如式(4)：

S[q(i)]=B[q(i)]-p(i)·q(i)

(4)

式中：q(i)为某时段乘客的出行需求量；B[q(i)]为乘客获得的收益，此乘客收益并非货币收入，而为乘客乘坐地铁带来的包括乘坐时间、速度、舒适度等心理效益；p(i)为第i时段地铁票价；S[q(i)]为乘客承受票价后的效益。对q(i)求导可得：

(5)

用户的效益最大化，导数值应为0，可得：

(6)

即：

(7)

常用的用户收益函数如式(8)[15]：

(8)

(9)

式中：p0(i)为第i个时段地铁票价的初始价格；q0(i)、q0(j)分别为第i、j个时段乘客的初始需求量；B0(i)为第i个时段用户的初始收入，即用户需求量为q0(i)时的收入；E(i)为第i个时段的价格需求弹性；E(i,j)为第i个时段对第j个时段的价格需求弹性。由于式(8)、式(9)除个别参数外形式相似，故以式(8)为例进行分析，同理可得式(9)相应公式或结论。对式(8)求导，得：

(10)

将式(7)带入式(10)，可得乘客需求量与票价的关系，如式(10)：

(11)

由式(11)可构建地铁收益函数与乘客效用函数。

2.1 地铁公司收益函数

参考相关文献[11]，结合对武汉市地铁的实地调研，拟将地铁时段分为5个时段，即：①发车—7:00，早高峰前平峰；②7:00—9:00，早高峰；③9:00—17:00，早晚高峰间平峰；④17:00—19:00，晚高峰；⑤19:00—收车，晚高峰后平峰。

在进行分时定价后，某一时段价格变化可能引起客流在不同交通方式的再分担，即为单时段响应。此外，不同时段价格的不同也可能导致乘客改变出行时段，实现需求量从高峰时段转移到平峰时段的目标，即为多时段响应。

根据以上分析，构建地铁收益函数如式(12)：

(12)

式中：R0为票价优化前地铁公司收益；p0为优化前的票价；C为地铁的人均成本，包括均摊的固定成本和每天运营维护的可变成本；q0(i)为票价优化前某一时段的客流量。实施分时定价优化后，地铁公司收益函数如式(13)：

(13)

2.2 乘客效用函数

对于乘客而言，地铁仅作为一种出行的方式，是其满足某种出行需求的工具而已，因此，地铁给乘客带来的收益仅仅表现为心理上的满足感，即效用S。在参考相关文献，并结合实际情况后，乘客效用函数由票价p、乘车候车总时间t和乘客舒适度φ等3个指标确定。各指标计算评判标准如下：

1)价格p

考虑票价优化后一定时间内乘客交通方式选择有限，公共交通网络仅考虑公交和地铁两种。一般情况而言，公交价格为固定票制，地铁为浮动票制。武汉地铁采用分段票制，即9 km以内(含9 km)为2元/人次，9～14 km(含14 km)为3元/人次，3元以上每增加1元可乘坐的里程比上一区段递增2 km，以此类推。由于分时票价目的在于寻找客流量与地铁票价的关系，并通过改变地铁票价调节各时期客流量，缓解客流不平衡矛盾，故票价采用连续变化函数更容易达到这一目的，得出更合适的运价率。一般而言，计程地铁票价函数可表示为[16]：

p=p′+δ·lij

(14)

式中：p为乘客出行地铁总票价；p′为地铁基本票价；δ为运价率，为笔者研究对象；lij为乘客乘坐距离，可用乘车时间与行车速度相乘表示。

2)时间t

时间t分为乘车时间和候车时间。对于乘车时间，大量的学者已经证明，乘客的乘车时长分布大致服从对数正态分布[5,17]，其概率公式如式(15)：

(15)

式中：T为乘车时间；μ为尺度参数；σ为形状参数。μ、σ均通过平均时长E(T)和乘车时间方差var(T)得到。

由正态分布的基本图像可知，在二分之一行车时间附近的乘车时间是大概率事件。因此，可以认为，在中途上下车的乘客为多数，即大多数乘客的乘车时间在二分之一行车时间左右波动。因此，用二分之一行车时长表示行人的乘车时间是合理的。

对于候车时间，乘客到站时间服从均匀分布，乘客候车时间采用发车时间的一半表示[18]。

3)舒适度φ

舒适性与乘车时间和乘车环境有关。车厢越拥挤则舒适性越差，反之越好。笔者以一节车厢内的乘客人数表示舒适度，人数越多，说明车内越拥挤，则乘客的舒适性越差。根据以上定义，舒适度函数计算式如式(16)：

(16)

式中：qi为一个时间段内某种交通方式的乘坐总人数；n为一列地铁的车厢节数；Tzc为某一时间段内小时数；tjg为某一时间段内的发车间隔。

根据以上分析，票价优化前乘客出行效用函数为：

(17)

式中：tw为候车时间；txc为地铁总行车时间。

票价优化后乘客出行的效用函数为：

S[q(i)]=B[q(i)]-p(i)·q(i)=-[α1·p+

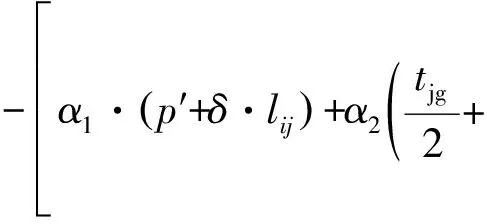
(18)

3 分时段定价优化模型

在确定客流量与票价的关系后，笔者对基于时间差别的地铁定价优化模型进行研究。

3.1 相关假设

为方便求解，做如下假设：①公共交通网络客流稳定，即短期内客流量增减幅度不会太大；②公共交通网络具有一定的独立性，即各线路之间互不影响；③地铁公司运营的收入仅考虑票价收入，且不考虑优惠票价的影响；④出行需求为多对多出行，任意两个站点之间均有客流需求，且客流受出行时间、票价等因素的影响；⑤乘客到达地铁站点的时间服从均匀分布；⑥公交地铁发车间隔均为不发车间隔，且每个时间段内各辆车的发车间隔相等且已知；⑦公交和地铁均为匀速行驶，地铁全天行驶速度形同，公交各划分时段内行驶速度相同；⑧研究仅考虑地铁价格改变后转移出的客流量，暂不考虑其他交通方式转入的客流量；⑨平峰期公交、地铁客流量不相互转移，即客流转移如图1。

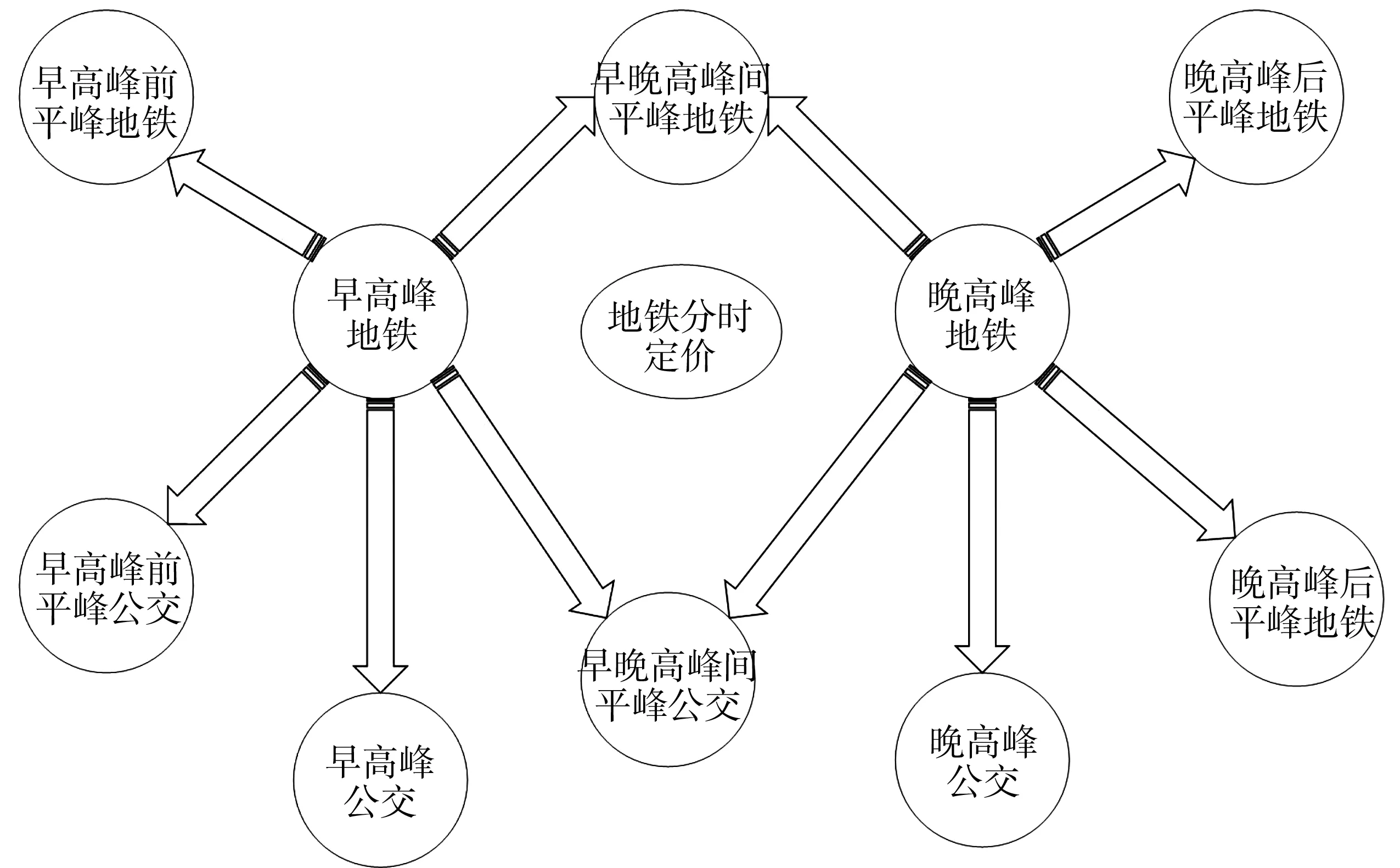
图1 分时定价后客流转移趋势Fig. 1 Transfer trend of passenger flow after time-sharing pricing

3.2 最大客流差最小化模型构建

为确保地铁的安全运营，模型以地铁最大客流差最小化，平衡地铁客流为目标函数。由此可得，目标函数应求得最小化的高峰期地铁负荷峰值和最大化的平峰期地铁负荷谷值。由于每时段小时数不同，故取时段客流除以时段时长所得的小时客流量衡量每个时段的客流负荷。最小化的高峰期地铁负荷峰值Qf、最大化的平峰期地铁负荷谷值Qg、最小化峰谷差Qf-g表达如式(19)～式(21)：

(19)

(20)

(21)

3.3 约束条件

约束条件从地铁公司效益、乘客效益和价格约束3方面构建。

3.3.1 地铁公司效益

目标函数以缩减最大客流差以达到削峰填谷为目的构建。在考虑目标函数实现的同时，地铁公司的效益问题不可忽略。目前，地铁公司多处于亏损状态，因而地铁公司效益已基本无缩减余地。相反，地铁定价策略应逐步以地铁公司盈利为目标进行。基于此，关于地铁公司效益的约束条件为票价优化定价后不会对地铁公司效益造成损害，即：

ΔR=R-R0≥0

(22)

由式(12)、式(13)可得：

(23)

3.3.2 乘客效益

地铁作为公共交通，其公共性是地铁定价的重要考虑因素，总的来看，其公共性可用乘客效益进行衡量。随着地面交通压力的逐渐增大，提倡公共交通出行成为主流。基于此，在对票价进行优化时，应考虑乘客总效益的变化，避免因效益损失过大带来大批乘客流失，加剧地面交通压力，故乘客效益损失应控制在一定范围，即：

|ΔS|=|S-S0|≤Sm

(24)

由式(17)、式(18)、式(24)可得：

(25)

3.3.3 价格约束

为了避免票价变化过高带来的乘客总效益下降，价格变动会有一定的范围，即：

p下限≤pi≤p上限

(26)

由式(14)可得，票价优化的实质是对运价率进行优化，即式(26)可变形为：

δ下限≤δi≤δ上限

(27)

3.4 求解算法

结合Pareto排序，采用遗传算法求解模型，具体步骤如下：

步骤1：令i=1，录入原始数据，包括票价优化前各时段客流量q0(i)、原始票价p0、地铁公司成本C、实施峰谷分时定价后运价率上限δ上限和下限δ下限。

步骤2：确定算法参数值，包括群体规模p、最大迭代次数G、交叉概率pc和突变概率pm。

步骤3：令i=i+1，由式(23)、(25)、(27)筛选δi的可能取值，产生随机初始化种群m。

步骤4：计算目标值函数。根据式(19)、式(20)、式(21)分别计算出最小化的高峰期地铁负荷峰值Qf、最大化的平峰期地铁负荷谷值Qg以及最小化峰谷差值Qf-g。

步骤5：通过Pareto得到个体的序位，并按序位对个体进行排序，最后根据排序值对个体分配选择概率。

步骤6：在由Pareto排序得出个体选择概率后，对群体进行选择、交叉、变异等操作，产生下一代群体后，重复步骤3，依次迭代，直至结束循环。

步骤7：输出结果。如果迭代次数g达到最大设定的迭代次数G，则算法终止，输出结果，得到各时段价格，再计算出最小峰负荷和最小峰谷负荷差。

4 算例分析

目前，某地地铁价格仍采用统一定价，即起步价2元，运价率为0.11元/km，公交价格为2元/次。二者均采用不等时间隔发车，以满足不同时期乘客的出行需求。此外，考虑地面不同时段路况的不同，公交的行驶速度也存在区别。公交、地铁分时段行车速度及发车间隔见表1。

表1 行车速度及发车间隔参数设置Table 1 Parameter setting of driving speed and departure interval

乘客效益函数相关参数取值见表2。

表2 其他参数设置Table 2 Other parameter setting

此外，各时段价格需求弹性见表3。

表3 各时段价格需求弹性Table 3 Price demand elasticity in each period

根据建立的地铁票价优化双层规划模型，采用遗传-Pareto算法求解，并利用MATLAB软件实现。运价率优化结果见表4。

表4 运价率计算结果Table 4 Calculation results of freight rate

由以上分时定价结果，可计算出地铁运价率为0.14元·km-1，大于实施分时定价前的0.11元·km-1。此外，具体各时段各方式转移客流量计算结果及各时段地铁分配客流量计算结果分别见表5、表6。

表5 各时段各方式转移客流量计算结果Table 5 Calculation results of passenger flow transferred by differentways in different periods

表6 各时段地铁分配客流量计算结果Table 6 Calculation results of passenger flow distributed inmetro at different periods 万人

地铁净收益为254.30万元，相较于票价优化前，净收入上浮185.45万元；乘客乘车效益值为-469.24，优化前乘客效益为-397.87，效益值下跌71.37；小时最大客流差为0.14万人，相较于优化前的0.16万人，小时最大客流差减小0.02万人。

由计算结果可知，地铁分时定价有利于地铁高峰客流的转移，减小高峰期客流拥堵情况，改善乘车环境，提升轨道交通利用率，增强乘客乘车体验，降低高峰期承载率，减小安全隐患，有利于地铁公司的运营。

5 结 论

利用弹性系数，参考电力、天然气等行业的用户需求响应模型，构建了地铁的用户需求响应模型，用于对地铁票价进行分时段优化，并利用遗传-Pareto算法对模型进行求解，最后通过算例，得到了优化后的分时段运价率，验证了模型。

笔者研究仍存在缺陷。首先，地铁票价优化后公共交通之间的客流转移仅考虑了地铁向公交的流动，而未考虑公交向地铁的流动。其次，由于弹性系数计算需要历史数据的局限，笔者模型验证仅参考国内城市地铁各项参数的算例分析，并未进行实际测算。下一步研究分析将从这两方面入手，以求构建更准确的地铁分时票价优化模型。