基于改进AHP和云模型的雷达软件系统安全性评价

夏 亮，项建涛，杨江平，王慧娟，张长聪

(空军预警学院， 武汉 430019)

雷达软件系统本身不会对人员和装备安全造成直接威胁，但是软件安全问题可能通过软、硬件的接口使硬件发生误动或失效，或者直接导致装备无法正常运行，造成严重的安全事故，影响正常的战备值班，目前，对雷达软件系统安全性研究较少，如何评价雷达软件系统的安全性是一个亟待解决的难题[1-5]。

常用的安全性评价方法有模糊评价法、层次分析法(Analytic Hierarchy Process，AHP)、熵权法、贝叶斯网络评价法等，例如王铁江等提出了一种软件安全性评估的模糊模型，利用软件测试过程中的客观危险失效的主观评价进行模糊推理，实现了软件安全性的定性评估[6]；刘威辰等基于AHP和熵权法对航空兵战术训练空域规划方案安全性进行评估，这一方法使评价的主观性与客观性都被充分考虑，具有较好的实用性[7]；涂俊翔利用贝叶斯网络描述了安全影响因素间的复杂依赖关系，构建了安全性评估模型，对机器安全性做出合理评价[8]。以上安全性评价方法在处理软件系统安全性评价问题上，不能够充分挖掘软件系统的耦合性和随机性因素，在将定性指标向定量评价转换时信息损失过多。

基于此，本研究提出了一种基于改进AHP和云模型的方法对雷达软件系统进行安全性评价，通过改进AHP方法可以更加合理的确定指标权重，通过云模型方法进行评价可以突出评价结果的耦合性、随机性和模糊性，为雷达软件系统更加合理、科学地进行安全性评价提供了一种新的思路。

1 雷达软件系统安全性评价指标体系

通过查找资料、部队调研、专家座谈，并结合雷达软件系统的自身特点，本研究按照3个层次构造雷达软件系统安全性评价指标体系，目标层是整个雷达软件系统的安全性，记为U；准则层是雷达软件系统的3个分系统的安全性，分别是终端分系统安全性、监控分系统安全性和信号处理分系统安全性，记为U1、U2、U3；指标层包括各个分系统下面的12个计算机软件配置项(Computer Software Configuration Item，CSCI)的安全性，分别记为U11～U33，具体的评价指标体系如图1所示。

图1 雷达软件系统安全性评价指标体系框图

2 改进AHP方法和云模型理论

2.1 改进AHP方法

传统的AHP方法都是通过元素之间的两两比较建立判断矩阵，然后通过求解判断矩阵最大特征根的特征向量来确定指标权重，假设有n个评价指标，要进行n(n-1)/2次比较才能确定判断矩阵，如此大的工作量容易导致专家判断出现失误，而且多次比较导致信息损失过多，不能客观反映指标的影响力。

因此，提出了一种改进AHP方法，该方法首先按照1～9的标度对各评价指标进行一次性打分，避免了重复冗余比较，更好地保留了各指标因素的信息，其次根据打分情况构造判断矩阵，最后按照AHP的方法确定指标权重。根据该方法确定的指标权重一定满足一致性要求，不需要额外进行一致性检验，具体的方法在评价流程中详细介绍。

2.2 云模型理论

云模型理论是基于传统概率统计和模糊集理论发展形成的一种综合评价法，能够实现定性概念和定量数值之间的相互转化，有效解决模糊概念的定量化处理[9-12]。

云模型包含三个数字指标，分别是(Ex,En,He)，其中Ex为期望值，最能够体现定性概念的一个指标，表示相应模糊概念信息转化为量化评价的中心值；En为熵，是期望不确定性的度量，表示数域中可被定性概念所接受的模糊度；He为超熵，是熵的不确定性的度量，表示云滴离散程度，揭示了模糊性和随机性的关系。

云模型通过计算机生成图像(Computer Graphic，CG)变化完成定性概念向定量数值的转换，其中CG分为正向CG和逆向CG，正向CG指的是从定性向定量的转换，输入云数值(Ex,En,He)和云滴数N，输出N个云滴的结果，如图2所示。

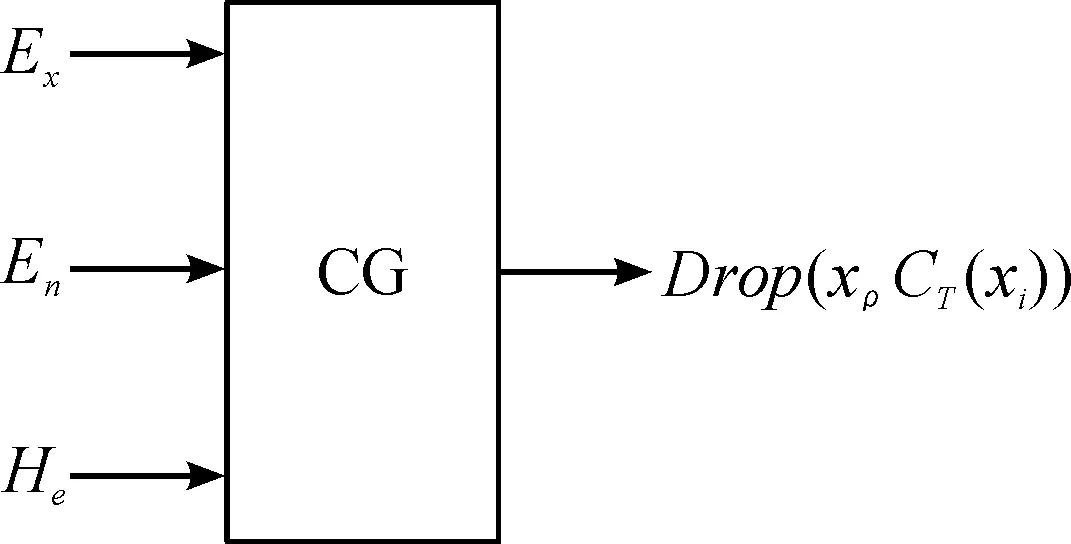
图2 正向CG

逆向CG-1指的是从定量向定性的转换，输入若干符合要求的云滴，得到云模型的3个数值，如图3所示。

图3 逆向CG-1

假设给定云C1(Ex1,En1,He1)和云C2(Ex2,En2,He2)的算数运算结果为C(Ex,En,He)，具体的运算规则如表1所示。

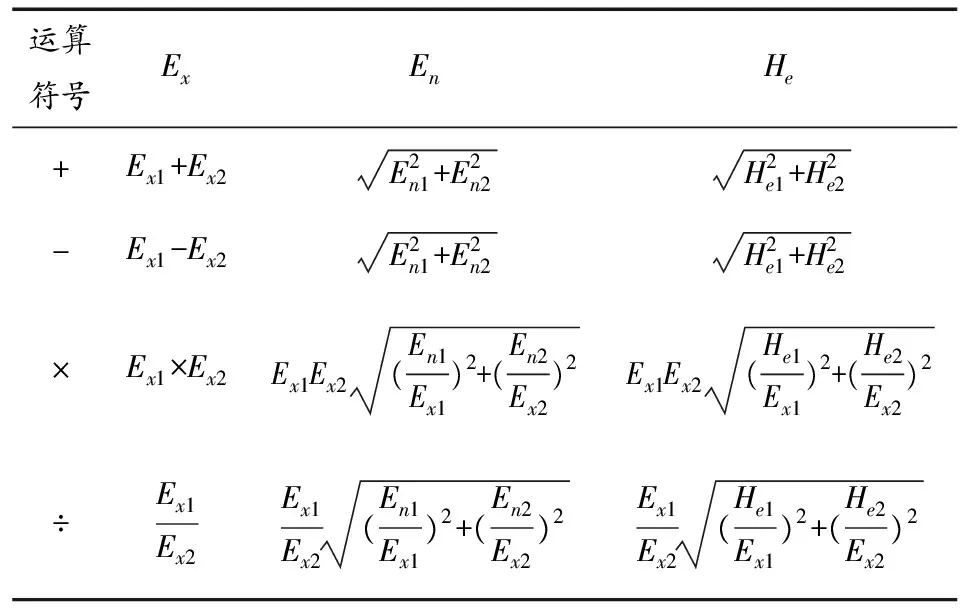
表1 云模型运算规则

3 评价流程

图4 云模型评价发生器

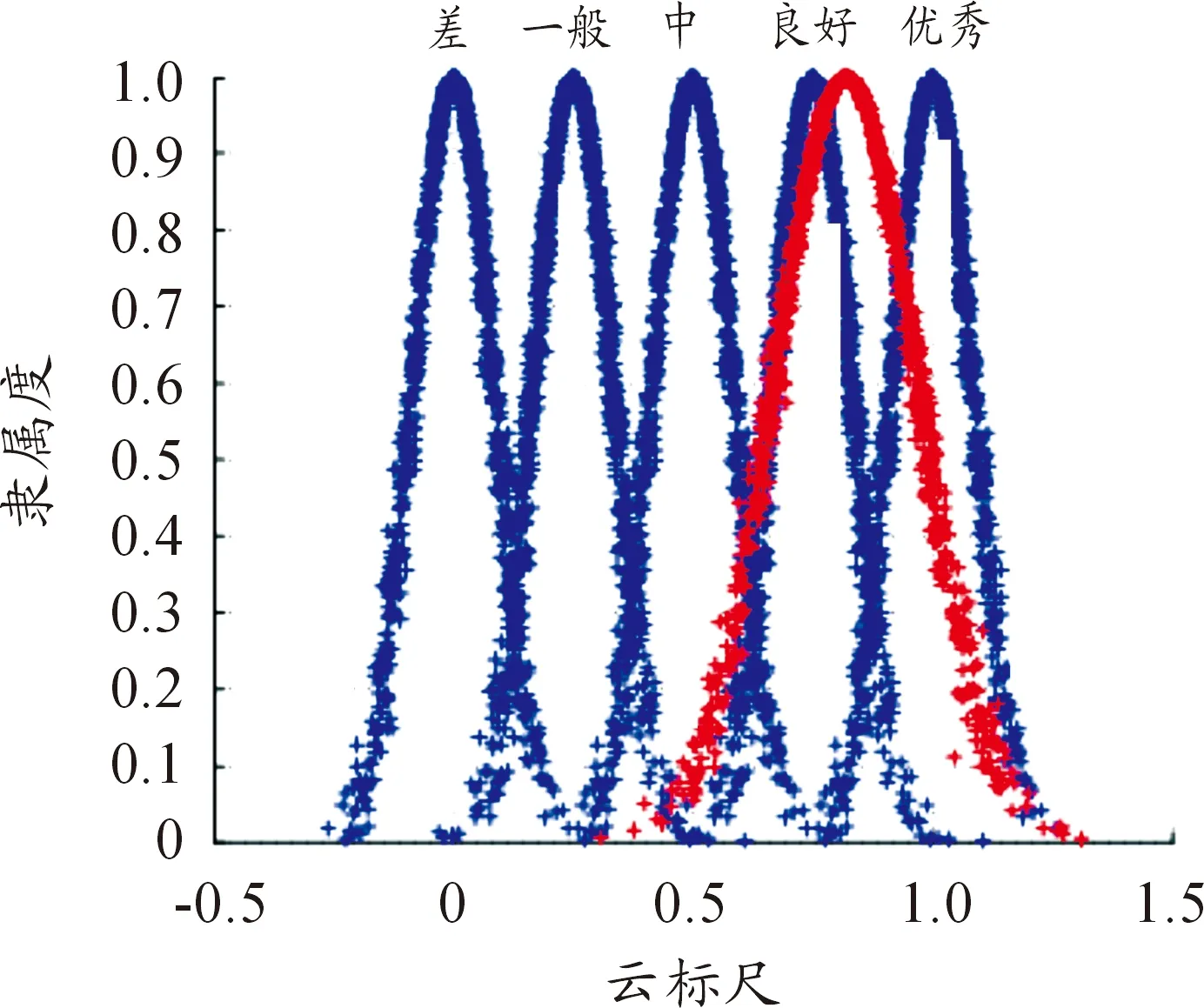
图4为Matlab仿真得到的云模型评价发生器，根据文献[13]可知，云模型服从正态分布，本文的评语集依次对应于云标尺中的5个正态分布的云模型，经过计算后得到综合云结果，然后将综合云结果置于本文确定的云模型评价发生器，与评语集对应的云模型进行对比，可以得到评价结果。

评价流程如图5所示。

步骤1对层次指标进行一次性打分

邀请来自部队、厂家和院校的专家组成专家组，根据指标的重要程度，按照1～9的分值对指标进行一次性打分，具体的分值情况见表2。

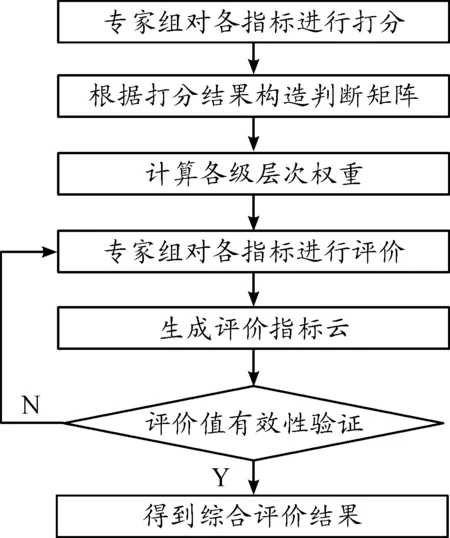
图5 评价流程框图

分值重要程度1极其不重要3不重要5中等重要7重要9极其重要2,4,6,8介于上述两相邻分值尺度之间

步骤2建立改进判断矩阵

通过打分情况建立判断矩阵的原理为，假设判断矩阵为A=(aij)n×n，n为指标的个数，bi和bj为同一判断矩阵中两个指标的分值，则aij可以表示为：

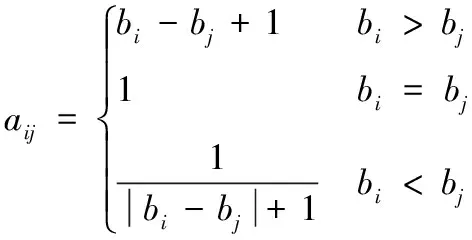
(1)

步骤3计算指标权重

(2)

(3)

根据式(2)和式(3)求出判断矩阵的最大特征值λmax和最大特征向量ωi，其中ωi为对应的指标权重。

步骤4对指标进行评价

专家组按照评语集对评价指标进行评价，将评价结果转化为具体的分值，对应关系为V={优秀，良好，中，一般，差}量化为(1,0.75,0.5,0.25,0)，组成评价矩阵Xi(xi1,xi2,…,xim)，i=1,2,…,n，式中n表示专家的个数，m表示指标的个数；然后通过云模型的逆向CG-1变化求出各个评价指标云的数字特征(Ex1,Ex2,…,Exm;En1,En2,…,Enm;He1,He2,…,Hem)，具体步骤见下。

步骤5生成评价指标云

1) 计算各评价指标的评价均值为

(4)

2) 期望值为

(5)

3) 评价的一阶绝对中心距为

(6)

4) 熵值为

(7)

5) 评价方差为

(8)

6) 超熵为

(9)

步骤6评价值有效性验证

步骤7综合评价云结果

将由改进FAHP求得的权重和由云模型求得的云数字特征进行运算，可以求得综合评价云，计算公式为

(10)

式中:m为指标个数，ωi为指标权重，得到的综合云为C(Ex,En,He)，将综合云代入本文确定的云模型评价发生器(图4所示)，并与评语集对应的云模型进行对比，相似度最高的评价等级对应的评价标准即为最终评价结果。

4 实例计算

步骤1对层次指标进行一次性打分

首先是对各层次指标进行打分，具体情况见表3所示。

步骤2建立改进判断矩阵

按照本文确定的规则，可以求得各层次的评价矩阵

表3 各层次指标打分情况

步骤3计算指标权重

根据式(2)和式(3)，可以计算出各指标的权重，如表4所示。

表4 各层次指标权重

步骤4对指标进行评价

邀请部队、院校、厂家组成的专家组10人对指标层进行评价，汇总评价表后，将各评价量化为相应分值，得到指标层评价矩阵为

步骤5生成评价指标云

根据式(4)～式(9)，求解准则层的评价指标云，得到的结果为U1(0.75,0.15,0.06)；U2(0.85,0.16,0.02)；U3(0.81,0.14,0.01)。

步骤6评价值有效性验证

通过对准则层各评价指标云结果的验证，发现U1不满足He

图6 指标U1云模型

造成这种情况的原因是专家对这个指标的评价存在较大差异，将评价结果反馈给专家组，然后由专家组经过反复研讨，重新进行评价，可以得到U1新的评价指标云，为(0.76,0.16,0.01)，如图7所示。

图7 指标U1改进云模型

步骤7综合评价云结果

根据式(10)，可以求得综合评价云结果为C(0.82,0.15,0.01)，将其代入云模型评价发生器，其云图如图8所示。

图8 综合云评价结果

根据图8可知，本文的综合云评价结果介于标准云“良好”和“优秀”之间，根据最大相似度原则，本研究认为雷达软件安全性评价结果为良好。

5 对比分析

将本文的方法与传统AHP法和云重心方法进行比较，其中与传统AHP方法主要比较指标权重确定方法的差异，与云重心方法主要比较评价方法的差异。

5.1 权重确定方法比较

以U2的权重为例，由传统AHP法确定的权重是(0.151 3 0.128 9 0.042 3 0.621 9 0.055 6)，将其与改进AHP法确定的权重进行比较，如图9所示。

图9 权重对比

从图9可以看出，由传统AHP法求出的权重存在个别指标信息损失过多、权重被弱化的问题；利用改进AHP法求得的权重既保留了各权重之间的相对关系，同时又避免了个别权重被弱化，而且对指标一次性打分避免了各指标两两之间的冗余比较，操作性更强。

5.2 评价方法比较

利用文献[11]确定的云重心评价法对雷达软件系统安全性进行评价，得到的云重心总加权偏离度为θ=0.762 3，将其代入云重心评价发生器，求得最后的评价结果为良好，与本文结果吻合。

将两种评价方式进行对比可以发现，利用云模型求得的评价结果更加直观而且更具有说服力，因为云模型求得的结果为C(Ex,En,He)，包含了云模型的三个数值，不仅得到了评价结果(期望)，而且还把云模型的熵(宽度)和超熵(厚度)也直观地展现出来了，使人能够一目了然且具有说服力，除此之外，云模型还对雾化严重的结果具有辨别力，当结果不符合云模型的检验条件He

6 结论

1) 确定了雷达软件系统安全性评价体系，为后续的评价奠定了基础；

2) 提出了一种改进AHP确定权重的方法，避免了指标之间的两两冗余比较和信息的损失；

3) 利用云模型评价方法对雷达软件系统安全性进行了评价，充分挖据了评价指标的耦合性和随机性，评价结果更加直观和具有说服力。

4) 本研究提出的这种评价方法对其他武器装备的评价亦具有借鉴意义。