基于Wiener过程和Kalman修正的速率陀螺仪剩余寿命预测

贺志远，吕卫民，胡文林

(海军航空大学， 山东 烟台 264001)

速率陀螺仪是导弹姿态控制系统的重要组成部分，它控制着飞行过程角速度的输出，一旦出现故障将影响飞行精度，导致飞行失控甚至弹体自毁。速率陀螺仪作为一种高精密的设备，内部包括众多电子元器件、传感器以及机械连接部分。它的性能随着工作时间逐渐改变，同时，受到环境因素(温度、湿度、振动)的影响，可能出现电路短路、断路、传感器失灵以及机械部件变形等失效。因此，对速率陀螺仪进行可靠性评估，合理预测剩余寿命，对于保证导弹的安全性具有重大意义。

传统的可靠性评估方法主要是根据失效机理建立模型进行失效分析，但是随着设备复杂程度的提高，很难建立起可靠的的失效物理模型[1]。针对这一问题，基于性能退化数据的分析方法出现，该方法利用设备性能随时间变化过程中的数据，建立性能退化模型，计算过程较为简便且结果具有较高的可靠度，已成为可靠性评估及寿命预测的重要手段之一[2-4]。目前，性能退化模型主要包括随机系数模型和随机过程模型。Lu等[5]最早使用随机系数模型研究退化过程，文献中假定模型的参数服从某种随机分布。这种方法的弊端在于，研究对象的参数一旦确定，其退化轨迹就确定，体现不出退化过程的随机性。而基于随机过程模型的方法解决了这一问题，该模型很好的体现了退化过程的不确定性，更加符合设备的实际退化规律。随机过程模型中主要包括Gamma过程和Wiener过程等， Yuan[6]建立Gamma过程退化模型对核电站某些元件的性能进行可靠性评估。王浩伟等[7]提出利用Gamma过程参数的非共扼先验分布进行Bayesian统计推断的剩余寿命预测方法。Gamma过程的退化增量是非负的，且严格单调递增，适用于单调变化的退化过程。而Wiener过程具有不严格单调的特性，计算分析特性较好，适用于退化过程具有波动性的产品。Park等[8]利用Wiener过程建立模型，对在加速应力条件下得到的退化数据进行处理。王小林[9]通过Wiener过程随机模型预测了金属化膜电容器的剩余寿命。

速率陀螺仪退化过程具有波动性，并非单调过程，本文采用Wiener过程建立随机模型进行计算。但是由于现实工作环境及设备本身的复杂性，退化建模过程还存在以下问题：① 设备内部组件较多，包含了电子部分和机械部分，退化规律不同，导致设备整体退化轨迹呈现非线性。线性Wiener过程已经无法有效的研究设备的退化过程，有些学者提出将非线性过程通过某种尺度转化为线性过程的方法[10]，王浩伟等[11]通过时间尺度转化方法将指数退化模型转化为线性模型对电连接器的可靠性进行了研究。虽然这种方法简化了计算过程，但结果的精确性也相应降低，而且有些退化模型无法转化为线性过程。② 不同于飞机等航空装备高频使用的特点，导弹装备的寿命更长，在全寿命周期内要经历不同的任务阶段，为了方便研究，分为运输、贮存、战备三个阶段，每个阶段的环境因素不完全相同，内部设备退化的主导机理也在改变，退化趋势呈现阶段性。针对多阶段退化问题，部分学者提出建立多阶段退化模型。袁庆祥等[12]引入转换函数改进Wiener过程，建立了多阶段退化模型预测电机的剩余寿命。该方法有效解决了多阶段退化问题，但是引入了新的函数，计算难度增大。

针对速率陀螺仪退化过程的非线性、多阶段的特点，本文采用Wiener过程建立非线性退化模型，利用收集到退化数据进行模型参数的估计，然后根据Kalman滤波算法对模型进行参数修正，实现退化过程的多阶段性，使剩余寿命预测结果更加精确。

1 剩余寿命预测模型

1.1 非线性退化模型

导弹寿命周期经历的环境因素复杂，内部设备的真实退化轨迹很难估计，也并非时间的线性函数，根据这一退化特点，本文建立基于Wiener过程的非线性退化模型。假设该设备退化过程只有一个关键性能参数，则非线性退化模型表示如下：

(1)

式中：X(t)为时刻t的性能退化量，X(0)为初始时刻的性能退化量(为了体现模型的一般性，令X(0)=0)；μ(t;θ)为非线性函数，显然，当μ(t;θ)=μ时，上式转化为一般Wiener过程；σB为扩散系数；B(t)为标准布朗运动。

1.2 寿命分布

当产品的性能退化量达到预设的临界水平时，就认为此时产品失效，这一临界水平称为失效阈值。假设该产品的失效阈值为ω，产品的寿命为T，且产品的性能退化轨迹由非线性Wiener过程描述，则产品的寿命T可定义为产品的性能退化量X(t)首次达到其失效阈值ω的时间，即

T={t∶X(t)≥ω|X(0)<ω}

(2)

假定μ(t;θ)和σB为固定未知参数，μ(t;θ)是关于t的可导函数，根据文献[13]，寿命T的概率密度函数为：

(3)

其中：

Ε(t;θ)=Λ(t;θ)-tΛ′(t;θ)

给定一个漂移系数λ，令μ(t;θ)=λbtb-1(b为固定参数)，寿命T的概率密度函数可表示为：

(4)

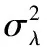
引理如果Z～N(μ,σ2)，A，B，C，ω∈R，那么

(5)

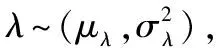
Eλ[fT|λ(t|λ)]

(6)

其中，p(λ)为λ的概率密度函数。

进一步可得，

(7)

可靠度函数可表达为：

(8)

1.3 剩余寿命预测

假设特定产品在tn和tn+l时刻的性能退化量分别为X(tn)和X(tn+l)，按照Wiener过程独立增量的性质，可得

(9)

令

Z(l)=X(tn+l)-X(tn)=

(10)

显然式(9)是一个由布朗运动B(l)驱动的新的随机退化过程。

产品的剩余寿命是指从当前时刻到产品发生失效时刻的时间间隔，根据寿命的定义可知特定个体产品在时刻tn的剩余寿命l可表示为：

L=inf{l∶X(tn+l)≥ω}

(11)

获得产品剩余寿命的关键是找到剩余寿命的概率密度函数。按照Wiener过程独立增量性质，结合式(9)、式(10)，可得

L=inf{l∶X(tn+l)≥ω}=

inf{l∶X(tn+l)-X(tn)≥ω-X(tn)}=

inf{l∶Z(l)≥ω-X(tn)}

(12)

特定个体产品在时刻tn的剩余寿命l，即随机过程退化量Z(l)首次达到阈值ω-X(tn)的时间。

结合式(3)、式(11)，可得tn时刻剩余寿命l的概率密度函数：

(13)

根据全概率公式，由式(13)可得，可靠度函数为式(14)：

(14)

2 参数估计

2.1 EM算法

上述非线性退化模型的未知参数设为Θ=(μλ,σλ,b,σB)。其中，b和σB为固定系数，描述各阶段退化过程的共性。μλ和σλ为随机系数，通过修正来描述不同阶段退化的过程的特性。

假设可测退化数据的设备有n台，分别在时刻t1，t2，t3，…，tm对设备进行测试，得到第i台设备在时刻j的性能退化数据Xi={X(t1,i),X(t2,i),…,X(tj,i)}，相应的退化增量为ΔX(tj,i)，因此

ΔX(tj,i)=X(tj,i)-X(tj-1,i)=

(15)

其中，λi为漂移系数的真实值。

未知参数增加为Θ=(λi,μλ,σλ,b,σB)。

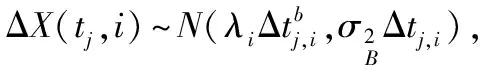
根据式(16)以及最优解搜索算法，可以得到未知参数的极大似然估计值，但计算过程较为复杂且未知参数数量较多，针对这一问题，本文采用Gibbs抽样算法来估计未知参数。

2.2 Gibbs采样算法

Gibbs采样是马尔科夫蒙特卡洛(Markov Chain Monte Carlo，MCMC)方法的一种，用于在难以直接采样时从多变量概率分布中抽取样本，尤其在高维参数的情形下，Gibbs采样有更大的优势。Gibbs采样算法实质上是M-H抽样时，接受概率等于1的特例，但由于其原理简单且适用范围广泛，因此被认为是一种特殊的抽样算法。

Gibbs采样算法的步骤如下：

1) 给定未知参数λi,μλ,σλ,b,σB的联合分布函数和先验分布函数，分别为p(λi,μλ,σλ,b,σB)和p(λi),p(μλ),p(σλ),p(b),p(σB)；

3) 计算出未知参数λi的条件概率密度，可表示为

(17)

同式(17)，分别计算其他未知参数的条件概率密度；

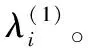
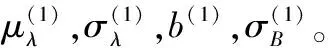
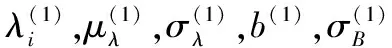
(18)

6) 使用收敛后的函数q(λi,μλ,σλ,b,σB)替代p(λi,μλ,σλ,b,σB)，重复3)、4)过程k次，得到k组Gibbs样本。

最后，利用k组Gibbs样本和贝叶斯公式计算未知参数的后验分布，进一步得到未知参数的估计值。

3 基于Kalman滤波算法的多阶段参数修正

Kalman滤波是一种高效的递归滤波器，建立在隐马尔科夫模型的基础上。它利用目标的动态信息，去掉噪声干扰，得到关于目标位置的估计。这个估计包括：滤波(对当前位置的估计)、预测(对将来位置的估计)和平滑(对过去位置的估计)[15]。

速率陀螺仪的退化过程具有明显的多阶段性，为了更加准确地预测剩余寿命，通过Kalman滤波算法对各阶段模型参数进行修正[16]，根据式(4)可知，修正对象为漂移系数λ。

假设在时刻tn进行漂移系数的修正，根据式(1)并结合Kalman滤波算法原理，选取状态空间方程如下：

(19)

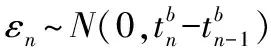
多种色釉于一坯胎中也是在近现代才流行起来，多种色釉的窑变比单色釉可说难，也可说易。难是难在对釉料料性的掌握，那种色釉流动，那种不流动，色釉与色釉之间能否结合，产生的效果如何，几种色釉结合当怎样的比例才能烧制出最佳效果等等，这就是难。说它容易，也只能说出现二次创作以后陶瓷艺术家才敢如此认为。颜色釉基础上的二次创作是根据艺术家对色釉窑变效果来巧妙装饰的，主观性较强，但选取的画面需要和色釉窑变气氛相吻合，才能达到异曲同工之妙。

误差项νδ可能是正值也可能是负值，这将影响到λn的正负，根据文献[17]，本文研究对象的漂移系数非负，为此确定了一个新的状态空间方程：

(20)

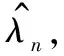
根据Kalman滤波算法及文献[14]，引入衰减系数γ(ti)。

γ(ti)=max{γ(ti),1}

(21)

且

其中，其中η为遗忘因子，0.95<η<1。

(22)

且

Pi|i-1=γ(ti)Pi-1|i-1

更新方差Pi|i。

(23)

最后，当i=n时，完成时刻tn漂移系数的阶段更新，修正后的退化模型可表示为

(24)

4 实例分析

通过对速率陀螺仪进行故障模式、机理及影响分析，发现寿命周期内其性能指标受到温度、湿度及振动等环境因素的影响。通过查阅相关文献，本文选取零偏值(°/h)作为性能退化指标。试验对象为6台速率陀螺仪，为了模拟该设备的工作特点，验证多阶段非线性模型的准确性，选取不同的温度应力(0～1 000 h，20 ℃；1 000～2 000 h，55 ℃；2 000～3 192 h，70 ℃)进行退化试验，试验过程共进行20次数据采集，每次间隔168 h，测试数据如表1所示。其中前4台测试数据用于模型参数估计，后2台测试数据用于多阶段参数的修正。试验的失效阈值设置为0.5(°/h)。

从图1可以看出不同温度应力下，零偏测试数据的退化存在着明显的差异，与上文多阶段退化的假设相符。

利用测试数据，通过Gibbs采样算法计算得到非线性退化模型的未知参数，再将计算结果与极大似然估计方法(EM)结果一起，列于表2。采用Gibbs采样算法，模型的拟合残差均方差(MSE)较小，说明该方法估计的参数更加符合实际数据的趋势。

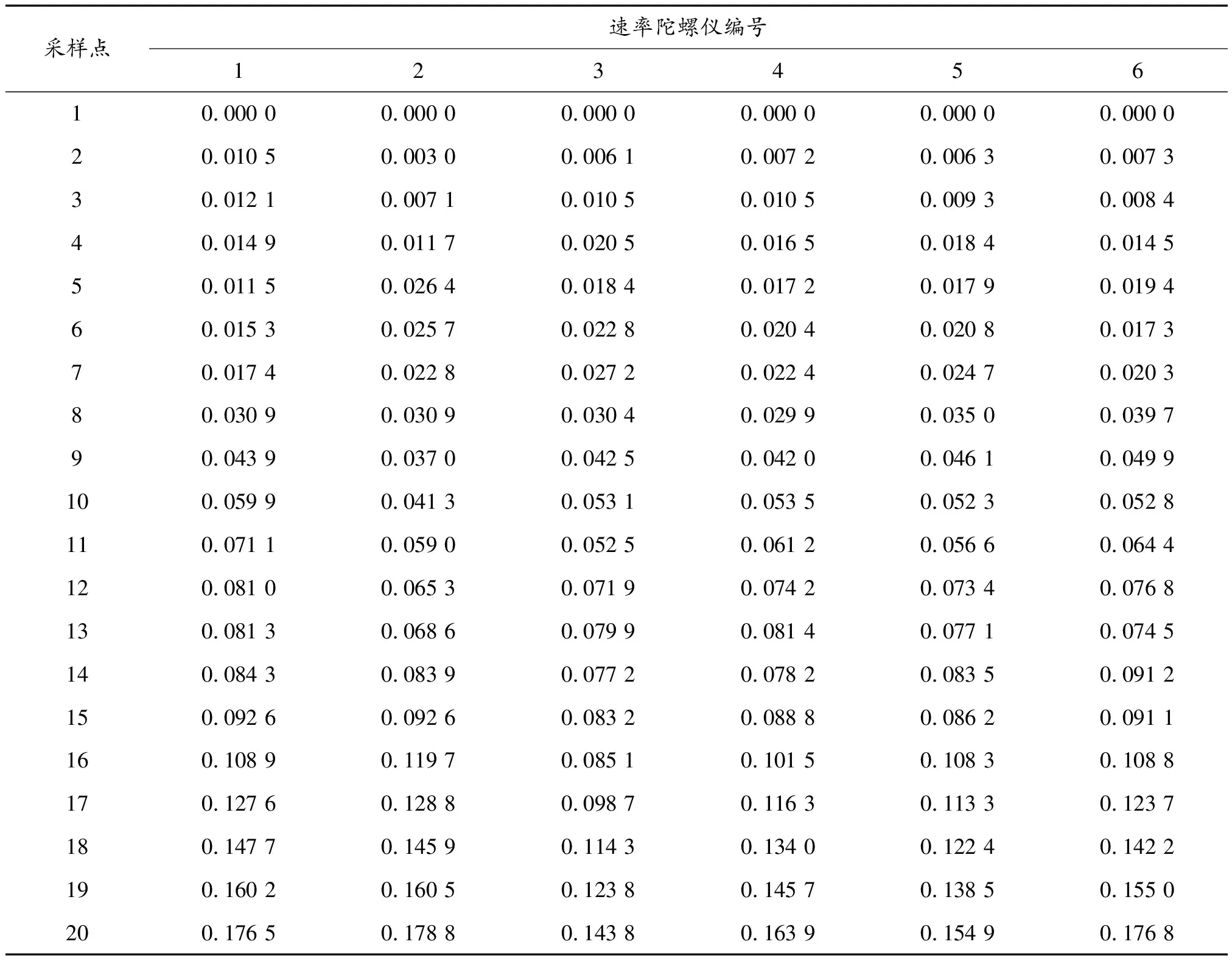
表1 速率陀螺仪零偏测试数据 (°/h)

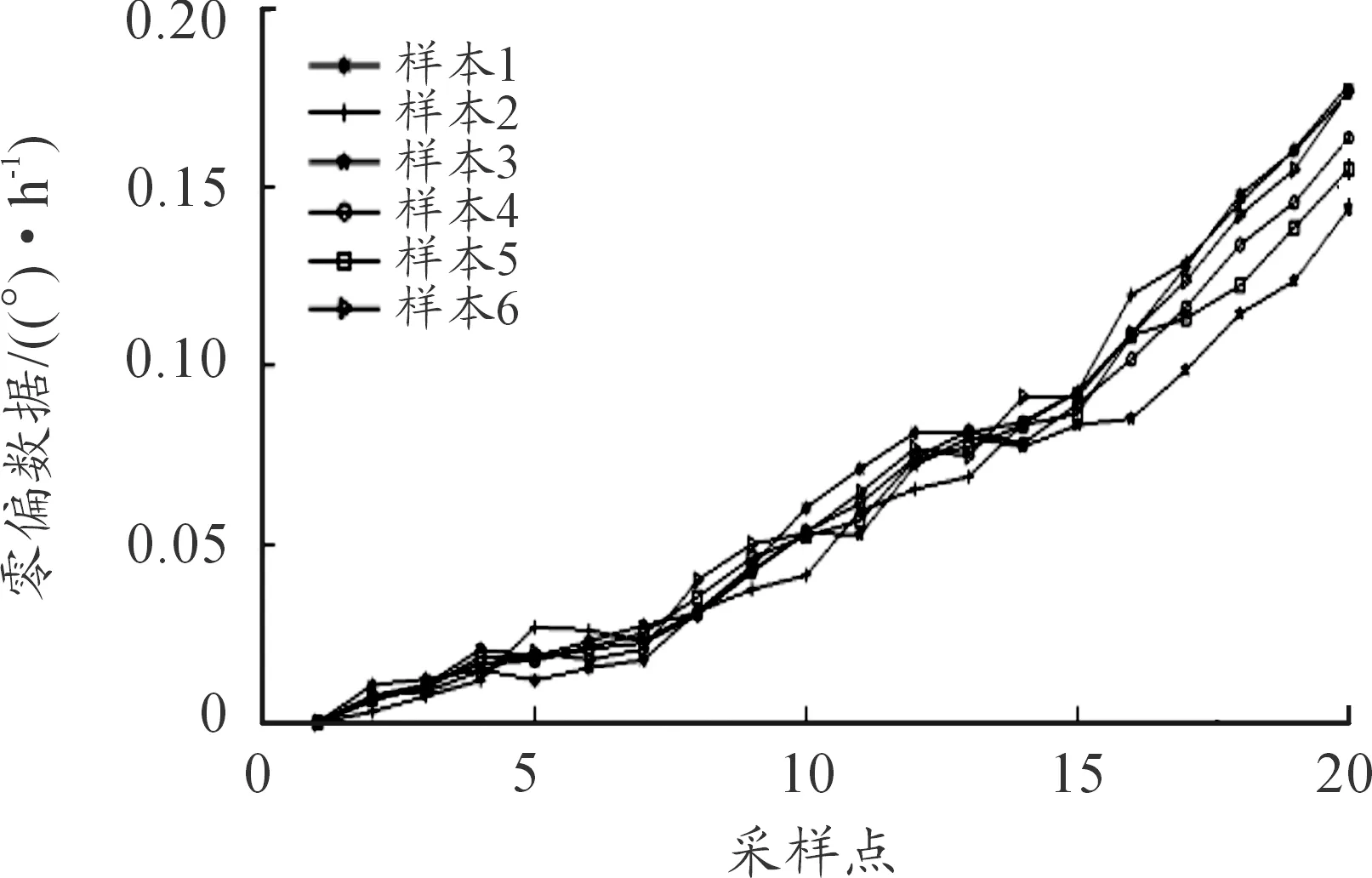
图1 零偏测试数据

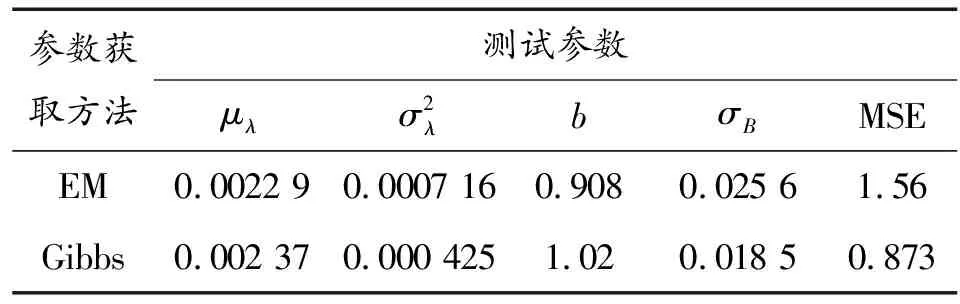
参数获取方法测试参数μλσ2λbσBMSEEM0.0022 90.0007 160.9080.025 61.56Gibbs0.002 370.000 4251.020.018 50.873

再运用Kalman滤波方法对各阶段退化模型的参数进行修正，修正后的参数如表3所示，并通过AIC准则与单阶段非线性退化模型参数进行比较，AIC值越小说明参数更加符合模型。

AIC=-2(maxl)+2p

(25)

其中，maxl表示最大似然函数的值；p表示模型未知参数的个数。

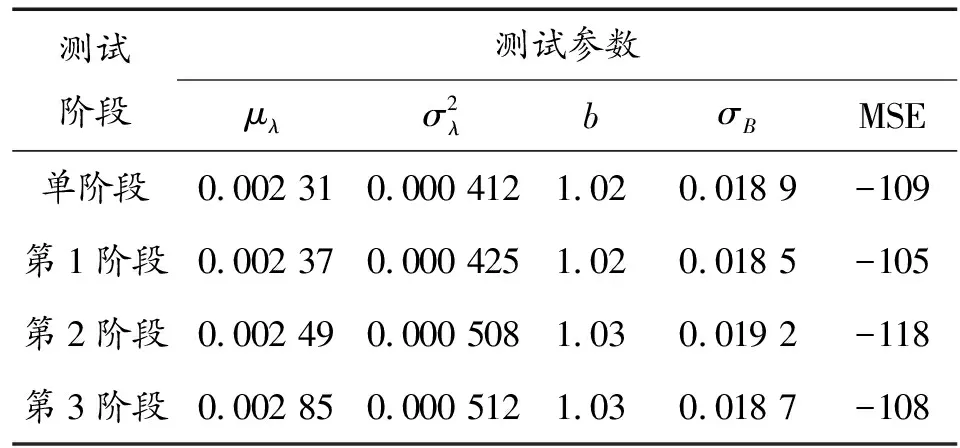
表3 不同阶段模型参数的修正值

从表3可以看出多阶段退化模型参数AIC的平均值小于单阶段退化模型，证明本文的多阶段参数估计方法更加精确，退化模型更加可靠。

最后利用修正后的模型进行剩余寿命预测，如图2所示。选取工作时间3 000 h，计算多阶段非线性模型和单阶段非线性模型的平均剩余寿命，分别为2 362 h和2 721 h。而在退化试验中，速率陀螺仪的平均失效时间为5 016 h。通过对比，本文所采用的基于Wiener过程的多阶段非线性退化模型所预测的剩余寿命更加接近实际情况。

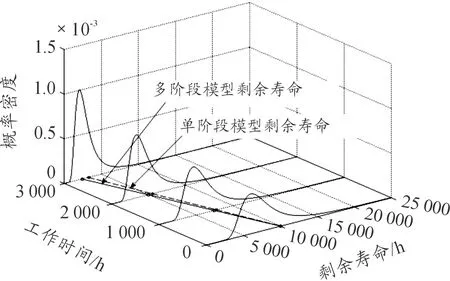
图2 剩余寿命预测概率密度

5 结论

1) 本文采用基于非线性Wiener过程建立速率陀螺仪的退化模型，使用Gibbs采样算法估计复杂模型的多个未知参数，并通过Kalman滤波算法进行漂移系数的修正，实现了退化过程的多阶段性。

2) 退化试验结果与不考虑漂移系数修正的单阶段退化模型相比，多阶段退化模型更加符合实际退化过程，对于剩余寿命预测更加准确。

3) 由于非实验条件下采集到的数据少且无效数据较多，使Gibbs采样算法计算精度降低。如何在样本少、干扰多的情况下估计模型参数值，需进一步研究。