基于ADC和模糊综合评判法的合成旅装备保障效能评估

宋 星，贾红丽，赵汝东，李正映

(陆军工程大学石家庄校区， 石家庄 050003)

高技术条件下的现代战争，装备保障的重要性愈加凸显，是否拥有较高的装备保障效能，成为制约战争胜负的重要因素之一。合成旅是军队改革后组建的新型作战力量，是我军适应信息化时代陆军建设模式和运用方式的重要探索。

对合成旅的装备保障效能评估，能够及时有效地掌握新型作战力量的装备保障系统现状，为装备保障建设提供科学的信息支持，对指导新编制体制下装备保障工作具有重大战略意义。装备保障效能评估[1]就是在一定的条件下和一定的时间内，按照一定的客观标准，对装备保障过程及其组成部分的保障模式、完成保障任务的好坏、保障反应速度的快慢、保障系统内部协调程度等等作出定量描述与评估的一种活动。

目前经典的评估方法有：结构分析法(ADC)、系统效能分析法(SEA)、层次分析法(AHP)、模糊综合评估法、指数法等。与其他方法相比，结构分析法(ADC)考虑了装备结构和战技术特性之间的相关性，强调了装备的整体性，能够较为全面地反映武器系统状态及随时间变化的多项指标，具有层次分明、结构简单、易于理解等优点[2]。

文献[3]以装备可用度为指标，采用蒙特卡洛仿真方法对装甲装备的装备保障效能进行了仿真优化；文献[4]采用ADC方法，对通信装备保障系统能力进行效能评估建模与分析；文献[5]在流水网络计划(FNP)技术框架下应用ADC模型对弹药调度系统保障效能进行了评估。以上评估多是对一种装备或系统的效能评估，而合成旅是军改后组建的新型作战力量，国内对于其装备保障效能评估的研究尚处于初始阶段，没有形成成熟的方法和手段。

ADC方法作为典型的效能评估方法，具有计算简单、易于实现的优点，在相关系统效能评价中应用较为广泛。因此，本文采用结构分析法(ADC)对装备保障效能进行评估。

1 结构分析法(ADC)

ADC方法又称为ADC效能模型，是由美国工业界武器系统效能咨询委员会WSEIAC(Weapon System Effectiveness Industry Advisory Committee)提出的一个经典的武器系统效能模型。该模型通过对系统中起作用的三个性能要素A、D、C进行分析，而后确定其内部的耦合关系，最后根据E=A×D×C计算武器系统效能[6]。

其中，矩阵A(Availability)表示待评估系统的可用度(有效性)，是对系统在开始执行任务时处于不同状态的概论。一般表达式为A=[a1,a2,…,an]，其中ai表示开始执行任务时处于状态i的概率。

矩阵D(Dependability)表示待评估系统的可信度指标，是对系统在开始执行任务处于某一状态而结束时处于另一状态的系统状态转移性指标的表述[7]。一般的，表示为：

dij表示在执行任务时系统由i状态转移到j状态的概率。

矩阵C(Capability)代表系统的固有能力，是系统在可用并可信的状态下，能达到任务目标的能力度量。一般表示为：

cij表示系统在i状态下达到j项要求的能力。

2 合成旅装备保障效能评估

从基于任务的角度来看，合成旅装备保障系统的可用度和可信度能够通过其完成主要任务的可用度和可信度来体现，即通过合成旅在完成任务过程中装备的平均可用度和可信度来反映。

2.1 可用度A

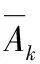
(1)

式(1)中，MTBF表示该装备的平均故障间隔时间；MTTR表示该装备的平均修复时间；MLDT表示平均保障延误时间[8]。

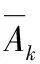
(2)

用a1,a2分别表示保障系统在任务开始时所处两种状态的概率，得到可用度向量A=[a1,a2]。其中，

(3)

(4)

2.2 可信度D

根据合成旅各主战装备系统的状态，可信度矩阵由4个元素组成，表示为：

(5)

当MTBF和MTTR服从指数分布时，设t为任务持续时间，则：

(6)

(7)

(8)

(9)

式(6)～(9)中，m为合成旅主战装备数量；λ为装备故障率；μ为修复率。

2.3 固有能力C

固有能力C的计算多采用AHP、品质效用函数或直接给出估值的方法，同以上方法相比，模糊综合评判可以做到定性和定量因素相结合，扩大信息量，使评价数提高、评价结论可信，很好地解决了判断的模糊性和不确定性问题[8]。因此，这里采用模糊综合评判的方法，对系统的装备保障能力C1进行评估，得到装备保障系统固有能力C1。其步骤如下：

步骤1根据装备保障的定义及装备保障任务区分，建立合成旅装备保障系统能力评价指标体系，见表1。

表1 装备保障能力因素集

步骤2分别确定一级、二级指标的因素集为：

U=[u1,u2,…,um]

Ui=[ui1,ui2,…,uik]

步骤3选取二级指标评价集V={v1,v2,…,vn}，将合成旅的装备保障能力分为v1(优)、v2(良)、v3(中)、v4(差)四个等级。

步骤4用AHP法和熵权法分别确定一级、二级指标的权重集为：

W={w1,w2,…,wm}

Wi={wi1,wi2,…,wik}

步骤5确定二级指标的评判矩阵为Ri=[rlj]k×n,l=1,2,…,k;指标rlj对于不同评语的模糊子集可由隶属函数确定，用指派方法[9]，四个等级分别属于偏大型、中间型、中间型、偏小型，采用梯形分布，设定隶属度函数为：

(10)

(11)

(12)

(13)

步骤6综合评判求B：B=W∘R；

模糊合成运算“∘ ”一般有四种计算模型，分别为:取大取小型、乘积取大型、取小上界和型及乘积求和型，需要根据具体实际来选取合成运算的计算方式[10]。

2.4 装备保障效能E

根据E=A×D×C求出系统的装备保障效能，并分析结果，得出意见建议。

3 实例分析

应用上述评估模型对某合成旅装备保障效能进行评估。由于合成旅主战装备数量等数据较多，不能全部列出，本文仅给出部分必要数据。

3.1 可用度和可信用计算

根据某合成旅各主战装备平均故障间隔时间MTBF和平均修复时间MTTR，平均保障延误时间MLDT，利用式(1)～式(4)计算出相应可用度向量为：

A=[0.998 0, 0.002 0]

根据式(6)～式(9)计算得到可信度矩阵D为：

3.2 固有能力C计算

3.2.1获取指标数据

通过“装备云”数据平台获取该旅装备保障相关数据，并对指标进行归一化处理，对于定性指标采用专家打分法(0～1)确定其最终值。指标数据见表2。

3.2.2确定权重集和隶属度

用AHP法和熵权法分别确定一、二级权重，由式(10)～式(13)计算各级隶属度，表3、表4和表5分别是最终确定的权重值和隶属度向量。

表2 归一化后的装备保障指标数值

表3 一级指标权重值

表4 二级指标权重值

表5 隶属度向量

3.2.3计算总目标的隶属度向量和装备保障能力

根据B=W∘R计算总目标的隶属度向量，归一化后结果如下：

从计算结果可以看出，该合成旅装备保障固有能力为良好以上，处于较高水平。

对照表6的评分表，计算该旅装备保障能力得分S=0.832。

表6 保障能力评分标准

3.3 装备保障效能E计算

E=A×D×C计算得到装备保障效能：E=0.752。从计算结果来看，该旅装备保障的固有能力得到了较大程度发挥，效能较高。但仍有较大提升空间，需要提高装备保障固有能力和装备维修水平。

4 结论

针对合成旅装备保障工作中的效能评估问题，在ADC效能评估的基础上运用模糊综合评判法计算装备保障能力C。以某合成旅装备保障相关数据为例，进行装备保障效能评估，验证了模型的有效性。结果表明，该旅装备保障固有能力较高，但实际发挥的效能不够，仍有较大提升空间，需要针对薄弱环节进一步加强训练，以提高装备保障效能。