基于运输安全的自适应多目标路径优化算法

吴耕锐，郭三学，吴虎胜，薄 鸟

(1.武警工程大学 装备管理与保障学院， 西安 710086； 2.武警警官学院 基础部， 成都 610213；3.武警警官学院 信息通信系, 成都 610213)

军事运输包含人员和物资(如武器装备、后勤物资等其他物资)运输，运输是从物资仓库到部队驻点的过程。处理大量重要物资的日常运输通常是由后勤保障部门完成。尽管运输任务是必要的，但运输安全也同样重要，尤其在军事运输中，由于运输的物资特别重要，更容易成为攻击目标，因此对运输路径安全性有特殊要求。

每次任务中，后勤部门收到部队驻点的需求信息。需求信息主要包括运输物资(人员)数量、到达目的地规定时间和装卸物资的OD位置信息，不同装卸位置会出现不同组合。例如，从一个中心节点装载军用物资并运送到另外一个军事驻点。

该问题属于有容量限制和时间窗要求的车辆路径问题，问题中包含了运输安全问题。相关的路径优化问题已在一些文献中有研究。比如王坤等[1]在弹药运输路径选择上进行了多目标优化，提升了弹药运输效率。黄军等[2]分析了军用油料运输安全风险影响因素，提出了安全风险的分析和识别方法。张梦得等[3]用弗洛伊德与蚁群算法对装备物资运输路径进行优化，简化了计算，解决了道路被敌人破坏时路径优化问题。张晓楠等[4]以运输成本和时间成本最小化目标，建立了预优化模型，并在实时调整阶段提出了基于调整成本期望的实时调整策略，使模糊需求车辆问题更贴近实际。陈希琼等[5]建立了同时考虑车辆容量和距离约束的双目标模型，构造了具有贪婪转移准则的多目标蚁群算法，实现了运输成本和路径间最大长度差最小化的目的。张萌等[6]在危险品运输路径研究上，建立了事故后果最小及运输成本最小的双目标，设计了处理大规模问题多项式，利于规避运输中重大事故问题。Y.Kang等[7]对危险品运输的公平因素提出了路径规划模型。

提高安全性的一种办法就是找到一条远离人群中心的路径[8]，另一种办法就是根据不同的非相似定义生成非相似安全路径。

从犯罪学研究运输路径安全性问题可知，恐怖分子会搜集攻击目标的相关信息，还会详细研究运输车队的路线等，增加车辆路径和行车计划变化性可以降低车队被攻击概率。周边社会经济人口密集地区易成为攻击目标[9]。例如，加拿大的一个研究发现，社会经济落后都与犯罪有很大关联，特别是突袭和抢劫[10]。

以上研究虽然考虑了运输路径的安全因素，但从本质上去研究路径问题，即对路径施加变化，降低路径本身可预测性的研究还不多，而针对路径易被攻击问题，以解决提升军事运输路径安全性的研究非常少。从以下因素考虑：按照相同的或者相似路径运输，车队容易被攻击；运输路径通过社会经济发达和人口密集地区，运输车队容易遭遇攻击。提出了一种综合安全风险度量，将综合安全风险度量作为自适应多目标随机路径选择算法的一部分，用于求解运输路径。算法是用k最短路径和IPM算法在每对OD节点上形成一系列非相似路径，根据车队历史运输路线，在之前路径中随机选择出部分路径，并把运输距离和运输安全值转化成权重和，将成本矩阵作为输入，在ALNS启发式基础上增加了自适应随机选择算法和时间调整算法来求解运输路径，进一步提高运输路径的安全性。其中，不同时间运输路径的变化示意图如图1。

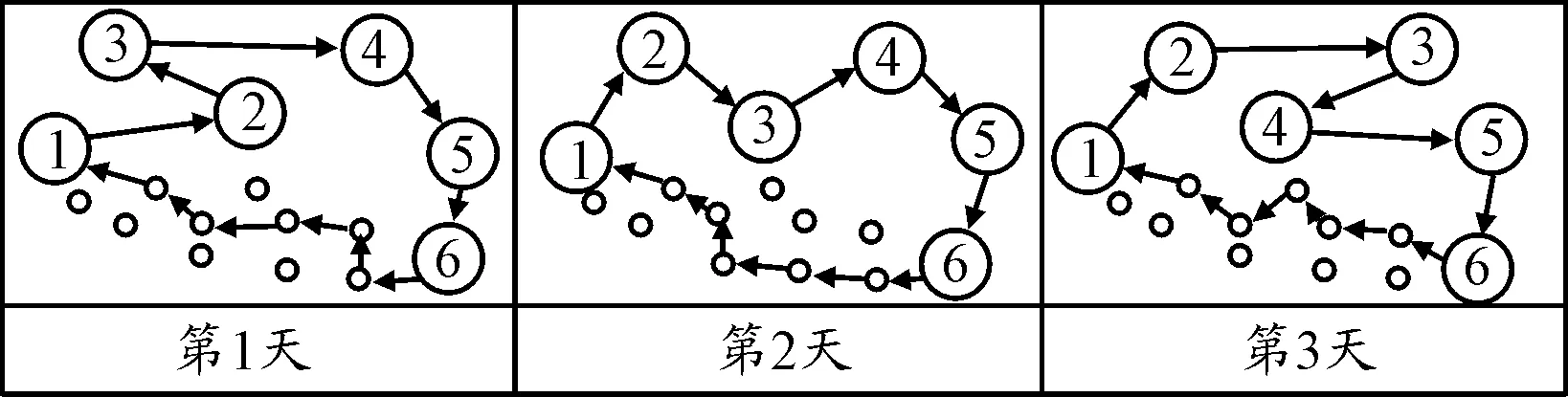
图1 路径变化示意图

1 问题描述

令G=(V,S)为一个有向图，V为顶点，RS为弧。弧(a,b)的长度为lab，顶点集由一个中心节点和需求点构成，即vo∈V和vn⊂V。算法就是在顶点集V的OD节点对之间生成一系列的非相似路径，并交替使用这些路径来解决运输路径问题。因此，令Dijk为路径k中顶点i到顶点j的距离，Nid为第i个节点在第d天的需求，Z为车队A中每辆车的载重量，目标函数是使运输距离最短和运输安全性最高。

1.1 综合安全风险模型

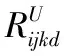
用地区的社会经济和人口密集条件值来计算顶点和弧的安全风险，同时将地区分为子地区或者周边地区，其中每个路径周边人口用低、中、高三种基于地区收入、教育水平的策略来计算，每种策略的人口权重值与其相应的安全风险相关。将顶点a和顶点b的弧的RS值定义如下：

(1)

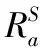
将顶点i和顶点j间的路径集Aijk中第k条路径的RS值定义如下：

(2)

数值包含了路径Aijk中每条弧的权重，弧越长，车队在弧上的行驶时间就越长，该路径就越不安全。这里假设路径周边地区的RS值固定不变，RU值会随着弧的使用频率变化而变化。

计算RU值时，每天都会计算相关路径弧的使用频率。RU值更新规则在一定程度上和指数平滑法相似。跟踪Ued值，即第d天所有路径中弧e所用的次数，是为了避免后续几天连续使用已用过的弧来使路径不可预测。因此，定义第d天弧e的预测计算公式如下：

Xed=α×Ued+(1-α)Xed

(3)

其中0<α<1为最近使用最频繁的弧的平滑因子。这表明Xed的值越小，运输安全性就越高。在一些初始化后，Xed出现较大值时需要对其进行调整。

(4)

其中，p是d天所有Xed值的平均值。

任意d天路径Aijk的RU值计算公式如下：

(5)

1.2 目标函数

将RU值和RS值合成一个综合安全风险度量值。令0≤Ka≤1和0≤Kb≤1代表两种安全风险的权重，将安全风险和每天运输距离成本优化相关联；令0≤Kc≤1。为第3部分的权重；令0≤Kd≤1为两种安全风险度量与Kd相关的统一权重，其中Kc+Kd=1。第d天路径Aijkd综合安全风险值计算公式如下：

(6)

第d天路径Aijkd成本计算公式如下：

Cijkd=Kc×Tc×dijk+Kd×Rijkd

(7)

其中，Rijkd表示综合安全风险值，Ta、Tb和Tc是平衡3种成本函数的缩放系数，使用缩放系数的主要目的就是平衡3种成本函数的影响。当Ta=1时，缩放系数就定义为综合成本值的平均值，Ta等于被RU值分割的RS值的平均值。Tc表示被距离分割的综合安全风险值的平均值。因为RU值每天都发生变化，所以要重新计算缩放系数。

用式(7)计算安全性最高的路径时，用自适应随机算法选出OD节点对(i，j)的特殊路径，并将这个路径的成本作为路径算法成本矩阵的输入。

2 求解算法

求解算法的描述如图2所示，提出了一个带成本矩阵的启发式算法，可以在短时间内求解出路径近似最优解。在预处理部分，每个节点对间会生成一个非相似数和最短路径；在每天开始时，根据前一天路径情况来更新RU值，在概率与它们距离和风险值成正比的路径中选择一条路径。

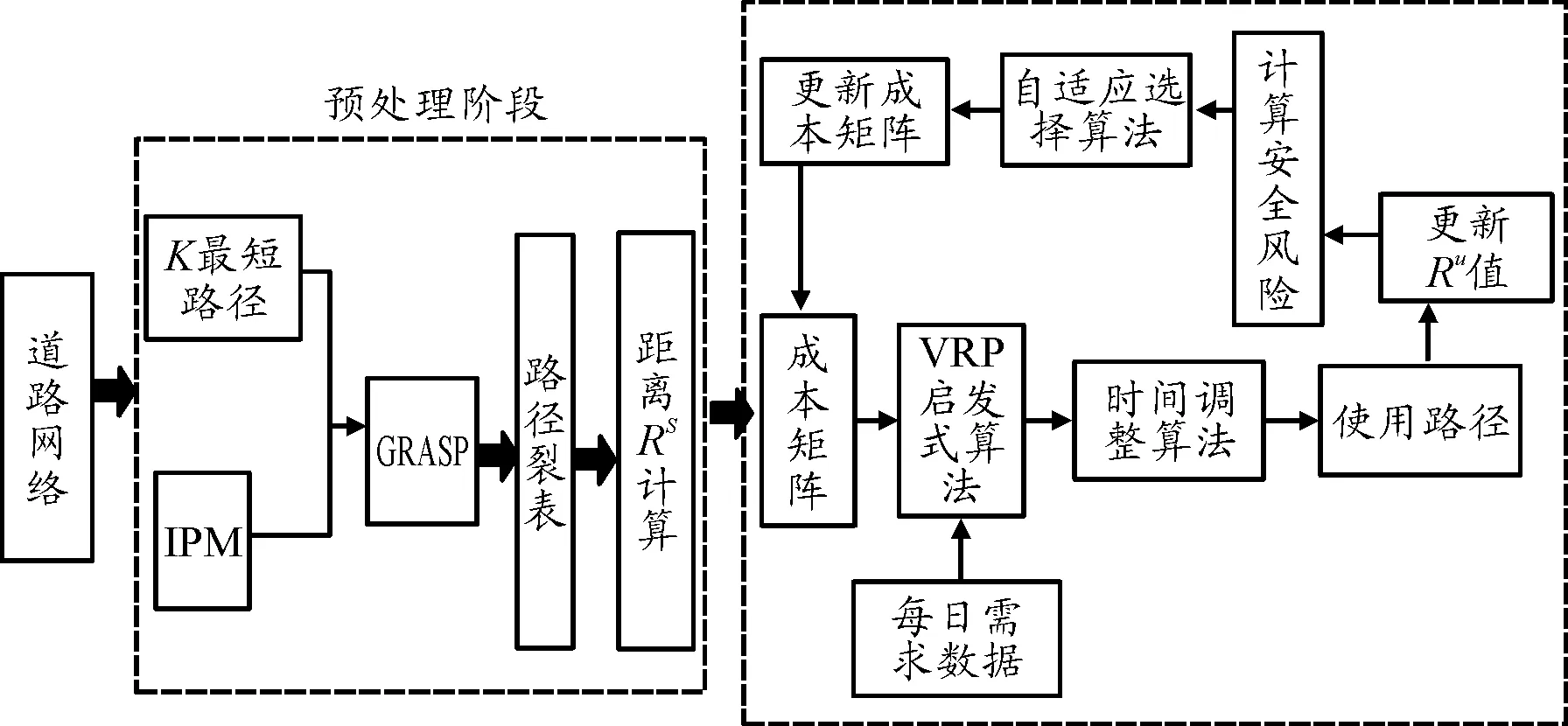
图2 算法流程框图

2.1 生成非相似路径

在每对节点(i，j)间生成替换Aij的非相似最短路径。一般来说，一系列短路径就可能包含很多共同的弧，弧分离的路径距离就可能很远。根据运输距离和非相似标准来选择路径，这个算法就成了用来求解双重目标路径非相似性的有效近似边界。步骤如下：

在每个节点对之间，用k最短路径算法生成15条候选路径，用IPM算法生成另外15条候选路径，从中选出10条无条件路径。算法首先随机消除高于非相似阈值的路径，然后迭代交换路径来改进路径的平均距离和非相似性，当达到最大迭代次数时停止。

通过所有路径中的配对非相似性来计算一条路径的平均非相似性。如果两条路径非相似，则该条路径的所有节点都远离其他路径的所有节点。为了测量路径1和路径2之间的非相似性，就要计算路径1到路径2的平均非相似性和路径2到路径1的平均非相似性，即路径1包含每个节点到路径2所有节点最短距离之和。路径2到路径1的非相似性计算也是如此。

求解算法的输入包含距离、RS值和这些路径的弧。通过该算法，可以求得平均距离短且非相似性高的路径集合。当路径生成之后，计算路径的RS成本。这些都是预处理部分的静态数据。

2.2 路径优化

应用路径优化算法，即算法1，确定每天的运输路径。在预处理阶段，应用成本矩阵生成第一天最短路径，对算法进行初始化；将成本矩阵和节点需求数据作为ALNS启发算法的输入，用于求解某一天的路径。在求得解后，算法会记录路径和所使用的弧，以更新路径中弧的使用频率，根据更新的频率值对RU值重新进行计算。为了便于规范更新所有路径的综合安全风险，算法将RU值规范在0～500，用于计算所有路径的综合安全风险值。

算法1路径优化算法步骤可总结如下：

第1步：初始化；

第2步：对于每个(i，j)节点：

1) 生成路径集AijAij={Aij1,Aij2,…,Aijk}，Aijk的距离为Dijk；

3) 选择节点(i，j)间最短路径作为初始路径。

第3步：当t=1，Nd时，进行循环：

1) 构建选择路径的成本矩阵；

2) 用ALNS算法求解路径问题，得到每辆车的路径总距离和安全风险值；

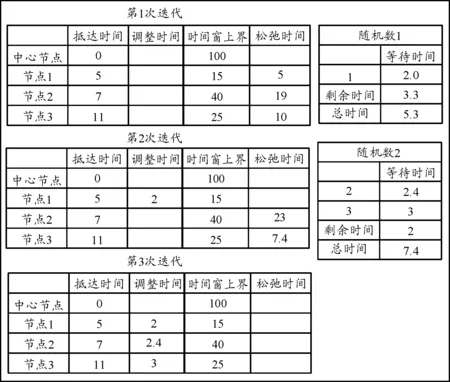
3) 如果t

① 记录ALNS解中使用的路径和弧；

② 更新所有弧的使用频率；

③ 计算所有路径的RU值；

④ 更新所有路径的综合安全风险值；

⑤ 应用自适应随机选择算法来选择OD节点对间的新路径。

2.2.1自适应随机路径选择算法

算法用于选择下一天所用路径。对于每个(i，j)节点对，算法为Aij中路径设置了一个选择概率，该概率与路径的成本成反比，路径的距离和安全风险就归并到决策者考虑的权重当中，根据前一天的RU值来调整选择概率。因此优化过程可以避免连续访问顺序节点。

该过程会随机选择路径，生成多样化路径集。每天生成的路径不一样是因为：访问节点需求不同；不同的成本矩阵值，生成的访问节点顺序不同；车辆随机抵达时间有调整。具体算法步骤可总结如下：

第1步：初始化；

2.2.2路径算法

这里使用ALNS算法，算法开始时有一个初始解，每一次迭代执行破坏和修复机制后，生成一个新的更好的解，在迭代一定次数后得到一个可能的最优解。

2.3 抵达时间调整算法

随机性和安全风险效应能提供一定的抵达时间多样性，为了增加同样需求节点抵达时间的变化性，使用调整算法来灵活分配与时间窗相关的节点访问时间。在时间窗上界和车辆抵达节点时间之间定义了一个松弛时间。调整算法是路径算法后处理部分的输出，每辆车运行独立调整算法。调整算法没有改变路径的顺序，所以路径的总距离和安全风险不变，只是在当前抵达时间上增加了调整时间。调整时间是插入在两个连续需求节点抵达时间之间的时间。在额外的时间间隔里，车辆可以停在两个需求节点中任意一个节点上，也可以停靠在两个需求点间的一个安全位置。分配多个停靠点的松弛时间可以降低车队停靠在单独一个位置的安全风险。将等待时间随机分割成不同位置的较短的等待时间，可使路径变得不可预测，从而提高路径的安全性。算法每一次迭代中，找到最低松弛时间，随机分成时间小块，并插入抵达时间子集当中。具体算法3步骤可总结如下：

第1步：初始化；

第2步：记录当前节点为节点O；

第3步：当当前节点不等于最后访问节点时，进行循环：计算路径A当前节点到最后一个节点的松弛时间；令当前节点最小松弛时间为tmin；在当前节点和前一个节点间随机分配最小松弛时间tmin；增加随机数作为调整时间，修改抵达时间。

迭代时，首先是计算所有需求点的松弛时间。当车辆在一个位置停留一个较长的松弛时间，其安全性较低，如果将松弛时间随机分成两个部分，就变成了两个不同地点的较短时间的停留，其路径安全性显然比较高，路径不可预测性得到加强，不同地点中车辆的等待安全性也就更高了。因此要将松弛时间被随机分成两部分，用一个随机数来确定被选需求点的松弛时间，这里称之为剩余时间，随机数代表路径随机性，以提高安全性。其中节点1的松弛时间最短是5.3。其次对于每个被访问节点来说，生成的随机数除去剩余时间后，将增加到抵达时间中作为时间调整。最后在每次迭代中添加和更新时间。第一次迭代后，下一个最小松弛时间为7.4，这个时间被分配到节点2和节点3。调整时间分配算法示意图如图3。

图3 调整算法示意图

用随机数来确定被选需求点的松弛时间的一部分，是为了增加路径的随机性，即车辆在不同地点的等待时间变成随机，让其无法预测在某点的具体等待停留时间，当然其随机数也是有相应时间取值范围的，不可超过时间上界要求，因此这里随机数来确定松弛时间是具有准确性的。

调整算法在初始可行解基础上进行，只是增加了抵达时间，没有违反时间窗可行性，因此不用考虑时间窗的下界。在这里虽然没有考虑时间窗下界，但实际工程应用中时间窗下界的影响是存在的，会出现个别情况时间下界数值较大时，会引起车辆服务质量时效性下降，影响整体的运输旅行时间，也可能造成一定程度的燃料浪费。

3 实验与结果分析

为验证算法对路径安全性、使用路径和访问节点顺序变化的影响，用两个不同数据集测试，第一个数据集中，对单独一天的需求求解，并对同样需求10 d的数据进行求解；第二个数据集中，对连续30 d求数据求解。数据集选择连续10 d和30 d，一方面是使数据具有连续性而不是单一随机的，另一方面取整，且取10的倍数，是为了便于计算。通过改变运输距离和安全风险目标权重对5种条件下算法进行测试：

条件1：安全性最高，不考虑距离(Kc=0,Kd=1)；

条件2：安全风险规避(Kc=0.25,Kd=0.75)；

条件3：安全中立态度 (Kc=0.5,Kd=0.5)；

条件4：愿意冒险的态度(Kc=0.75,Kd=0.25)；

条件5：距离最短，不考虑安全性(Kc=1,Kd=0)。

实验可知，需求不变时路径在不同天里的变化情况，算法有效。

运输安全值量化的思路如下：基于使用频率的安全风险(RU)和考虑第k条路径周边的社会经济和人口情况RS值，用这两个运输安全值来量化运输安全，一方面RU值增加时代表路径使用重复的路径频率高，使用了的相同路径概率高，其路径不可预测性就会降低，即路径安全性较低，相应数值也就较大，相反当其数值较小时，路径重复使用频率就降低，路径变得不可预测，安全性就变高，因此用其值大小可衡量路径安全性高低；另一方面，根据相关研究文献结果可知，RS值大小也与路径安全性高低相关，RS值大时，安全性降低，RS值小时，安全性就提高。

3.1 数据和实验环境

数据地点是中国北京。第一步应用GIS软件平台ArcGIS 10.3生成道路网络，初始化网络图如图4所示，包含 9 627个节点和 18 645条弧。平台中生成的相同节点和弧能够被消除，以此降低求解时间。消除既没有需求又不是中心节点的3种不同情况如图5所示。

1) 节点有一条输入和输出弧，节点被消除，输入和输出弧合并成一条弧；

2) 当输入弧的尾部和输出弧的头部相同时，节点被消除；

3) 节点有两条输入弧和两条输出弧，一条输出弧同时是节点的出入弧时，节点被消除，与此相关的4条弧合并成两条弧。

在消除节点后，节点数下降到1 865个，弧的数量下降到3 736条。尽管大部分节点是道路连接点，但生成和选择的替换路径的OD点数量会变得很大。算法预处理部分包含处理运输网络和生成不同节点对之间的替换路径，算法后半部分是在实验分析前进行批量处理。

图4 初始化道路网络图

图5 节点减少的预处理过程

通过对100个不同需求节点进行处理，可知不同节点位置越多，需求节点增加越多，计算量就越大。因此，额外的实验时间是可控的。

这里使用的是连续10 d和30 d北京驻军某部的真实需求数据。一天内需求节点的数量在50～150变化，需求值在0～6 000，包含15辆载重5 000 kg的军用卡车，车速在40～60 km/h。实验环境是64位Intel(R) Core(TM)i7-4800MQ CPU 2.70 GHz和16 GB 内存。

3.2 实验结果

首先，用算法求解连续10 d有相同需求数据的路径解。5种不同距离和安全权重条件下的求解情况见表1。

表1 10 d路径求解结果

从结果可知，优化路径时，只考虑距离最短，安全值就会很低，这个可以用RU值来衡量。因为使运输距离最短也会降低RU值，所以RU值很大程度就成了安全风险值。

反过来，正如预期的一样，短路径会频繁使用同一条弧。当生成路径时，只考虑使安全性最高，路径距离就变得很长。与条件5相比，条件1的路径距离长26%，安全性高47.7%。可知目标函数的安全风险权重增加时，路径安全性就明显提高。

在条件3下，当决策者对运输距离和运输安全风险保持中立态度时，与条件5相比，其运输距离长14.6%，安全性高38.7%。

分5种情况对目标函数中距离成分权重对总运输距离的影响进行量化，其具体描述如图6所示。可知，从条件1到条件5，决策者所冒的风险更多，总安全风险值呈一个增加趋势，而总距离是一个线性关系变化。

图6 连续10 d的距离和安全风险值

弧作为影响路径安全的一个指标，主要衡量指数是弧在不同天的使用频率。5种条件下一条弧在不同天里的使用频率分布情况如图7。分析得出，弧被使用的频率越高，则路径安全性就越低，当目标函数中安全风险的权重增大时，同一条弧重复使用频率就降低。比如，在条件1下，10 d里23.8%的弧只用于其中1 d；相比而言，在条件5下，1 d只使用12.5%的弧，超过4.6%的弧每天都在使用。路径的变化不仅仅是因为算法的随机性，还因为在10 d里选择替换路径以及决策时安全风险的权重。当安全风险权重Kd增加时，说明决策者不喜欢冒风险，弧的使用频率就会降低。这表明，算法可避免重复使用同一条路径，特别是通过RU值来限制时，可实现这一目标。

图7 5种条件下一条弧在不同天里的使用频率分布图

算法运行效率方面，对连续30 d军事运输情况进行测试，结果见表2。其结果与连续10 d数据求解结果相似，可知运输距离和安全风险的相关情况：当安全风险的权重Kd从1减小到0时，安全风险值增加了47.6%，总距离减少了27.7%，5种条件下运输距离和安全风险值如图8，可知路径优化中包含安全风险目标的优点。

表2 30 d路径求解结果

图8 连续30 d的距离和安全风险值

通过表1和表2求解情况可知，在安全性权重Kd从1～0变化过程中，运输安全风险值也随之发生了相应得从小到大的数值变化，表1给出的10 d求解路径运输安全风险值从270.59逐渐增加到了399.76，表2给出的30 d求解路径运输安全风险值从407.33逐渐增加到了601.32，说明了安全风险权重大小与运输安全风险值的很好对应关系，说明其合理性。

通过验证调整算法对需求点抵达时间的影响，对比10 d里有同样需求的每一天，是否运用调整算法情况下的路径求解中抵达时间的区别，并计算了连续10 d 5种条件下每个需求节点的抵达时间的变化范围，如图9所示，平均抵达时间存在92%的变化。同时，对变化值进行配对T检验，得到ρ值比10-5小，表明调整算法会增加变化值，但没有超出需求节点抵达时间变化范围，而每个需求节点的抵达时间是通过连续10d最大和最小的不同抵达时间来计算的， 5种条件下调整算法对抵达时间范围值的影响如图10，可知平均时间范围有24.1%的变化。配对T检验表明：调整算法会增加范围值，但ρ值小于10-3。调整算法增加了抵达时间的变化性，提高了路径的安全性。

图9 调整算法使用前后抵达时间方差

图10 调整算法执行前后抵达时间范围

4 结论

为了实现多目标优化，将成本矩阵作为求解路径的输入，运用提出的自适应选择算法求解，降低路径弧的使用频率，根据弧的使用频率来更新RU值，应用随机机制使路径不可预测，并通过定义松弛时间，使用调整算法使抵达时间多样化。

通过对北京地区驻军某部实际需求节点的数据测试，结果表明：算法降低了相同路径的使用频率，量化了运输距离和安全目标，调整算法实现了抵达时间多样化，提高了路径安全性，验证了算法有效性，能较好为军事运输提供决策辅助。