某型火箭静态应力及地震响应谱分析

韩向阳，赵继广，段永胜，辛腾达

(航天工程大学， 北京 101416)

spectrum

在液体火箭等待发射状态中，环境的温度、湿度以及外界带来的振动、冲击、污染等因素的作用都在不同程度上影响其使用效能，特别是在地震等自然灾害面前[1]，火箭发射前状态的安全保证存在较多难题。箭体的抗震性能直接影响人员和设备的人身和财产安全，因此验证火箭整体的安全性，对箭体结构进行地震响应谱分析是十分必要的。

在振动条件下，Wenyong Tang等[2]提出了一种新的模型来研究贮箱内推进剂的晃动，包括波浪断裂，波浪冲击侧壁和圆底，介绍了液体晃动模型在仿真分析中获取的方法。朱琳等[3]分析液体燃料运载火箭的推进剂与贮箱的耦合振动时，采用精确建模、工程化快速计算及火箭液固耦合燃料系统等效模态参数，为火箭复杂液固耦合结构的三维精确模型的建立和工程化应用建立了基础。根据研究现状来看，目前地震激励下待发射状态箭体结构振动响应的研究方法较少，缺少比较优势，不能更好地反映结构振动特性。

本文采用响应谱分析法对某型火箭在地震激励下的结构响应进行评估，建立有限元三维实体模型，进行静应力分析，采用模态分析计算结构振动特性确定其固有频率和振型，通过地震响应谱分析从频域的角度计算箭体结构的峰值响应。

1 地震响应谱分析方法

结构抗震分析主要有三种方法：等效静力法、时间历程法和响应谱法[4]。等效静力法比较简单，但存在工程计算缺陷，而时间历程法计算结果最为准确，但计算耗时长，且较为复杂，相比之下响应谱分析更能有效反映结构响应特性。响应谱分析时，首先需要求解固有频率、模态振型等结构的自振特性。合理设计地震响应谱，确定结构阻尼，计算各阶模态系数，最后利用振型组合方法求解结构的峰值响应[5]。

2 有限元模型建立

2.1 火箭箭体结构描述

箭体结构是火箭的主体，由多个功能各异的部件和组件构成，包括有效载荷整流罩、仪器舱、级间段、氧化剂箱、燃烧剂箱、箱间段、后过渡段、尾段等。该型火箭为两级推进，箭体高32.9m，直径3.35m，起飞质量约241t，采用常规液体推进剂，氧化剂箱充四氧化二氮液体，燃烧剂箱充偏二甲肼。箭体的重要部件中，过渡环焊缝采用氩弧焊将箱底、箱筒和短壳连接在一起，并承受轴压、液压和内压。尾段位于一级箭体的末端，全箭通过尾段竖立在发射台上，它承受着箭体全部重量。

2.2 三维实体模型

模型建立过程中各部件采用绑定接触、模拟螺栓连接和焊缝连接，对结果的影响较小，可以忽略。使用建模软件SolidWorks建立全箭的三维实体模型，如图1所示。

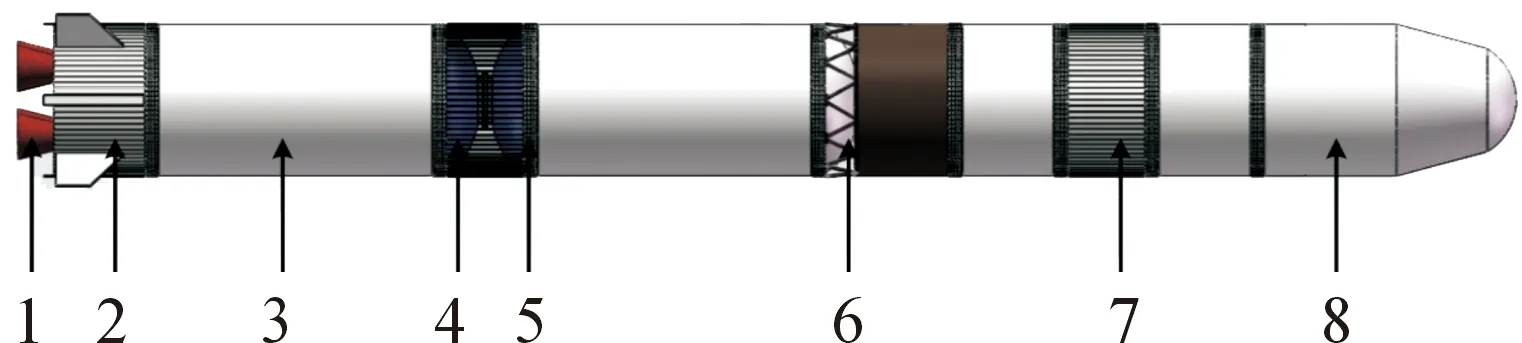
1.发动机；2.尾段；3.一级燃烧剂箱；4.前底；5.短壳；6.级间段；7.箱间段；8.有效载荷整流罩

2.3 材料属性及边界条件

箭体结构的主要材料为高强度铝合金2014、2024型号，主要部件材料物理参数值列于表1。箭体通过尾段的四个发射支座与地面发射台连接，作为位移约束固定，竖立在发射台上。

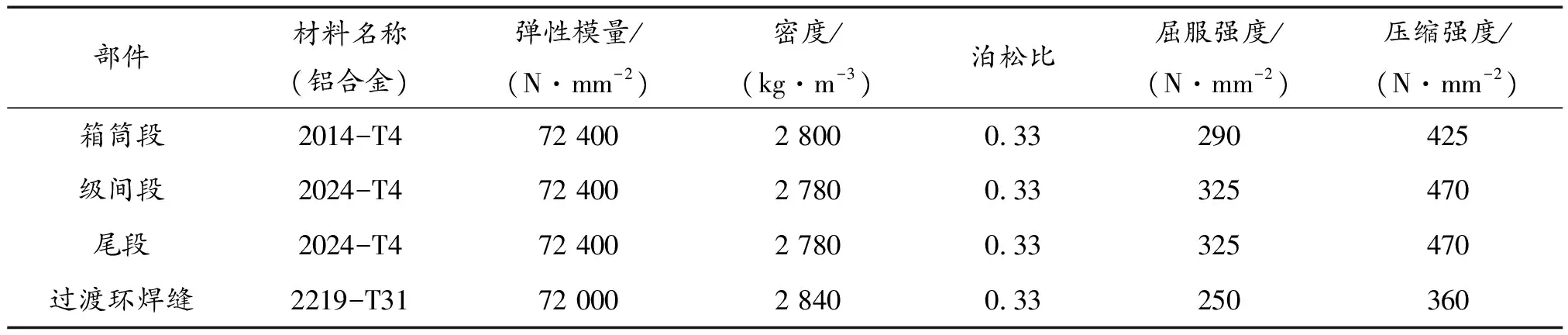
表1 箭体主要部件材料物理参数值

3 静力学分析

箭体自身受地球重力的作用，尾段承受全箭约241 t的重量，贮箱箱筒内加注完成液体推进剂，箱筒承受轴压、液压和内压，根据火箭竖立的实际状态对模型施加合理的约束条件和定义边界条件。固定尾段4个发射支点，载荷为标准地球重力，以Y轴负方向加载至整个箭体，箱筒内压为2个标准大气压0.2 MPa，进行静应力计算，其等效应力云图如图2所示。

从图2可以看出，推进剂加注完毕后在竖立状态，箭体的最大应力为203.37 MPa，主要作用在尾段的支点处，小于材料的屈服强度，满足强度要求。

图2 箭体结构等效应力云图

4 火箭结构模态分析

模态分析是计算结构振动特性的数值技术，是其他动力学分析的基础，响应谱分析需要在其基础上进行。结构振动特性包括固有频率和振型，确定结构的固有频率和振型，可以使结构设计避免共振，并预测在不同载荷作用下结构的振动形式[6]。在前述静力学分析的基础上添加Modal模块，求解箭体在此工作状态环境下的频率和振型，提取影响较大的前10阶模态频率[7]，如图3所示。

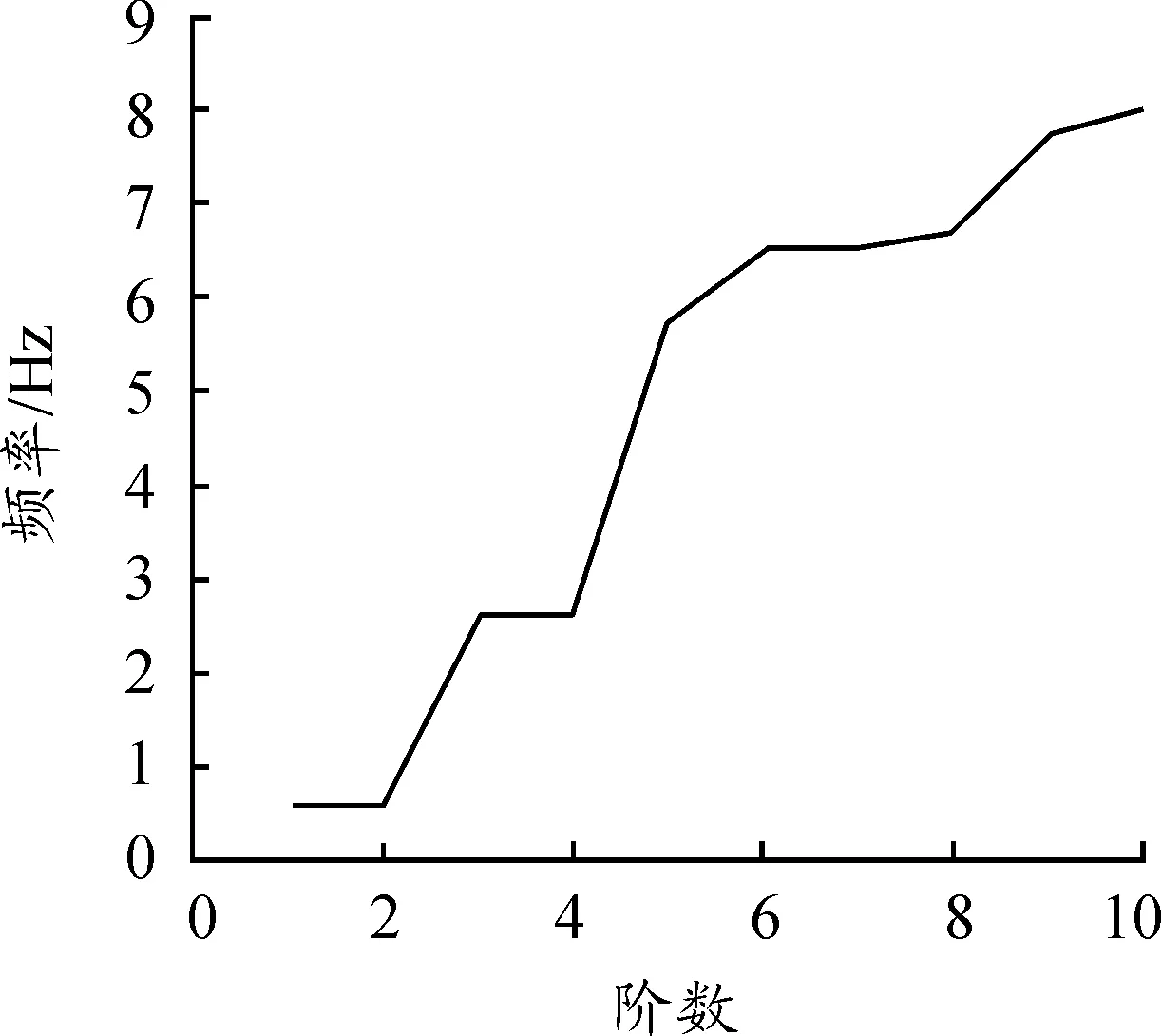
图3 箭体前10阶模态频率

通过前10阶频率数据分析，发现频率集中在0.5～8.1 Hz范围内，其中1阶和2阶，3阶和4阶，6阶和7阶频率基本相同。由于存在相似模态振型，研究相应模态的变形，仅具体分析第1、3、5、8、9、10阶模态，从左到右、从上到下依次排列，如图4所示。

图4 箭体各阶模态振型

由于按照真实1∶1变形，软件工作界面只能显示肉眼难以识别的微小位移，因此图4中采用自动放大倍数，可以清楚辨认振型特点。根据模态求解结果，总结前10阶模态频率和振型特点，如表2所示。

表2 箭体前10阶模态频率及振型特点

5 箭体地震响应谱分析

5.1 响应谱的描述与设计

对于响应谱分析方法，要求输入的是频谱激励，对一特定的地震波，可以通过实测或计算机求出一系列具有不同频率的单自由度系统的最大位移、速度和加速度，可以分别表示为频率的函数，这些关系曲线就是这个特定地震波的响应谱。地震响应谱分析是将复杂结构简化为若干振型叠加，每个振型转化为一个单质点体系。任何复杂结构的地震响应，都可以由若干个单质点体系响应叠加求得。具有固有频率的单自由度系统可根据响应谱求解出对地震波的峰值响应。

在没有本地地震波谱的情况下，采用目前结构抗震分析时常用的7级地震波El-Centro波作为输入[8]，该地震波N-S(北-南)向、E-W(东-西)向以及V(竖直)向峰值加速度分别为3.487、2.141、2.101 m/s2，分别与Workbench界面总体坐标系的X向(水平)、Z向(水平)以及Y向(竖直)相对应，地震波时程曲线如图5所示。

地震波时程曲线较为形象客观，可以对箭体进行瞬态动力学分析，分析结构在随时间任意变化的载荷作用下的动态响应。理论上时程分析是最准确的结构地震响应分析方法，但是由于其分析的复杂性，且地震波的随机性，只是把它作为响应谱的验证方法，一般并不直接使用。因此本文采用傅里叶变换将时域信号转换为频域信号，进行响应谱分析。Seismo Signal作为地震数据处理常用软件[9]，可以将时域信号转换为频域信号。

将El-Centro地震波数据载入Seismo Signal软件，经过基线校正和Butterworth滤波，设置带通滤波频率区间为[0.1 Hz，25 Hz]，获得地震频率的傅里叶变换曲线，如图6所示。图6中数据显示:频率为1.464 Hz时振幅达到最大为2.971 dB，说明地震波在此频率作用最大，而且主要作用频率均在箭体前10阶频率范围内。

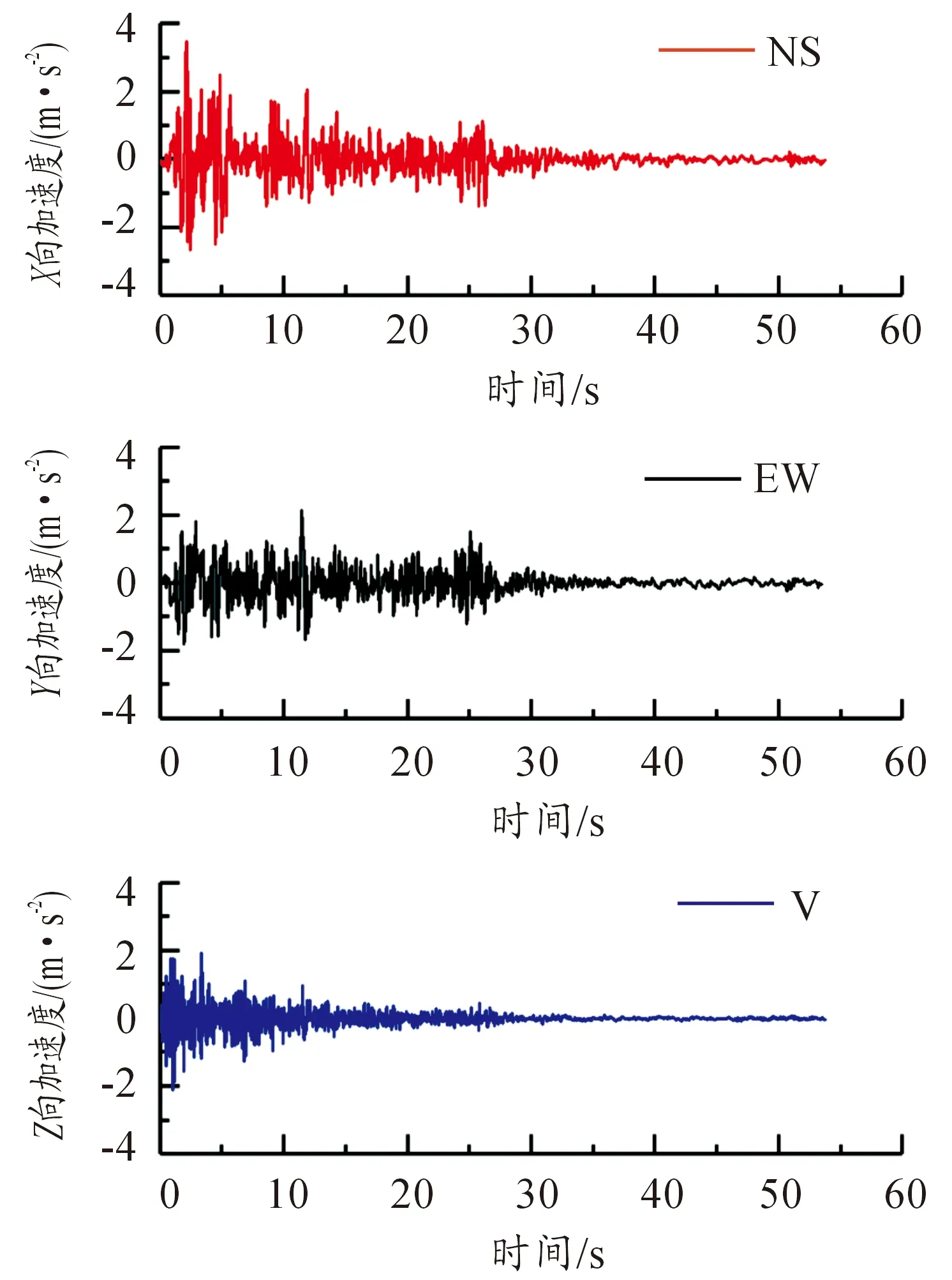
图5 El-Centro波加速度时程曲线

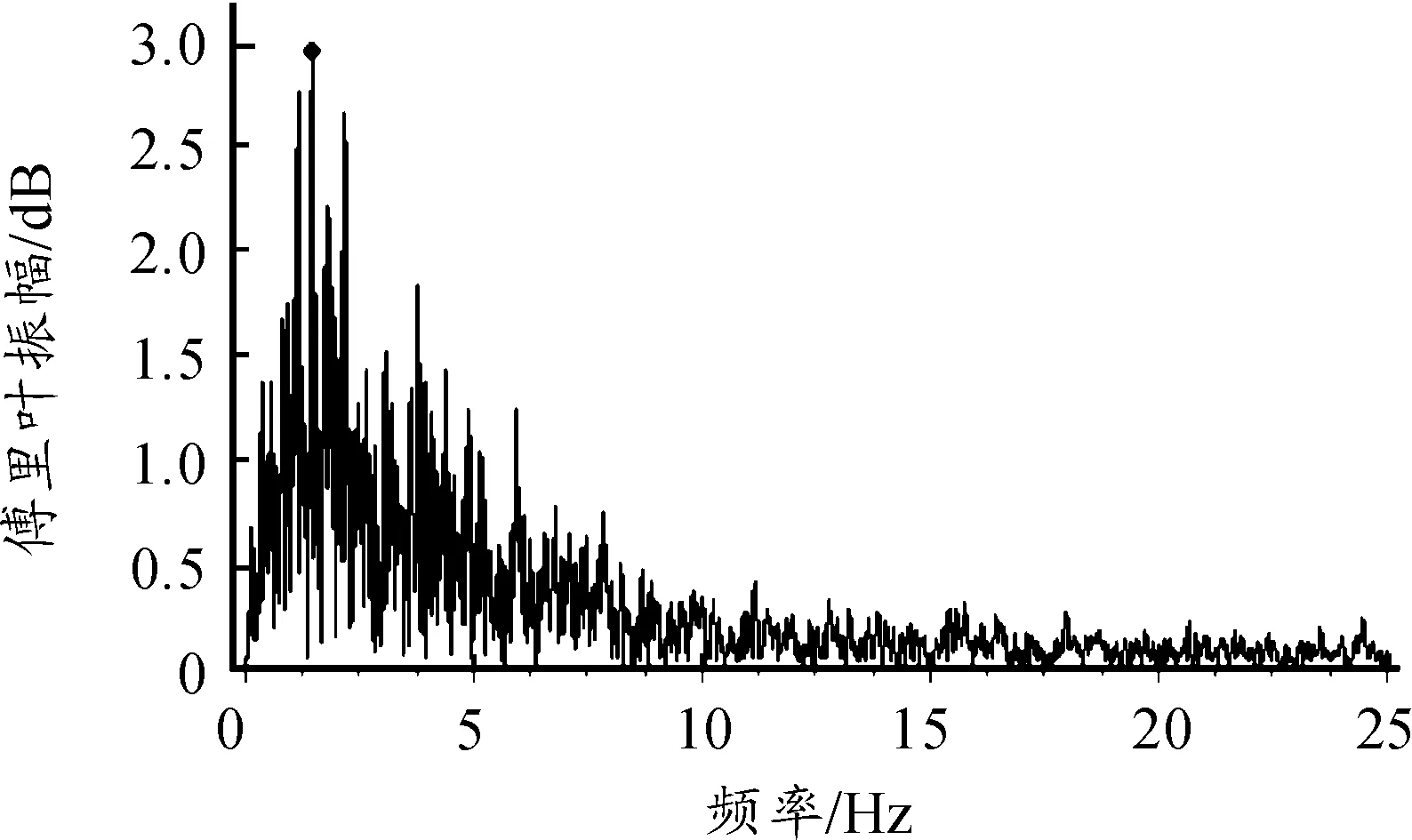
图6 傅里叶变换曲线

经过数据拟合求解，设定0.1的阻尼值，得到El-Centro波的加速度频谱如图7所示，位移频谱如图8所示。

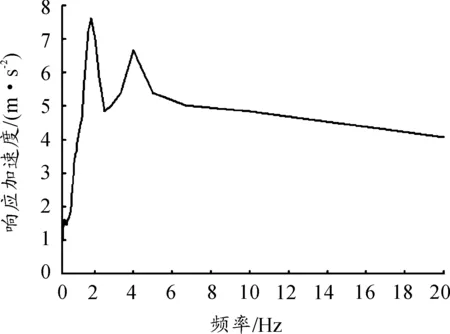
图7 响应加速度频谱

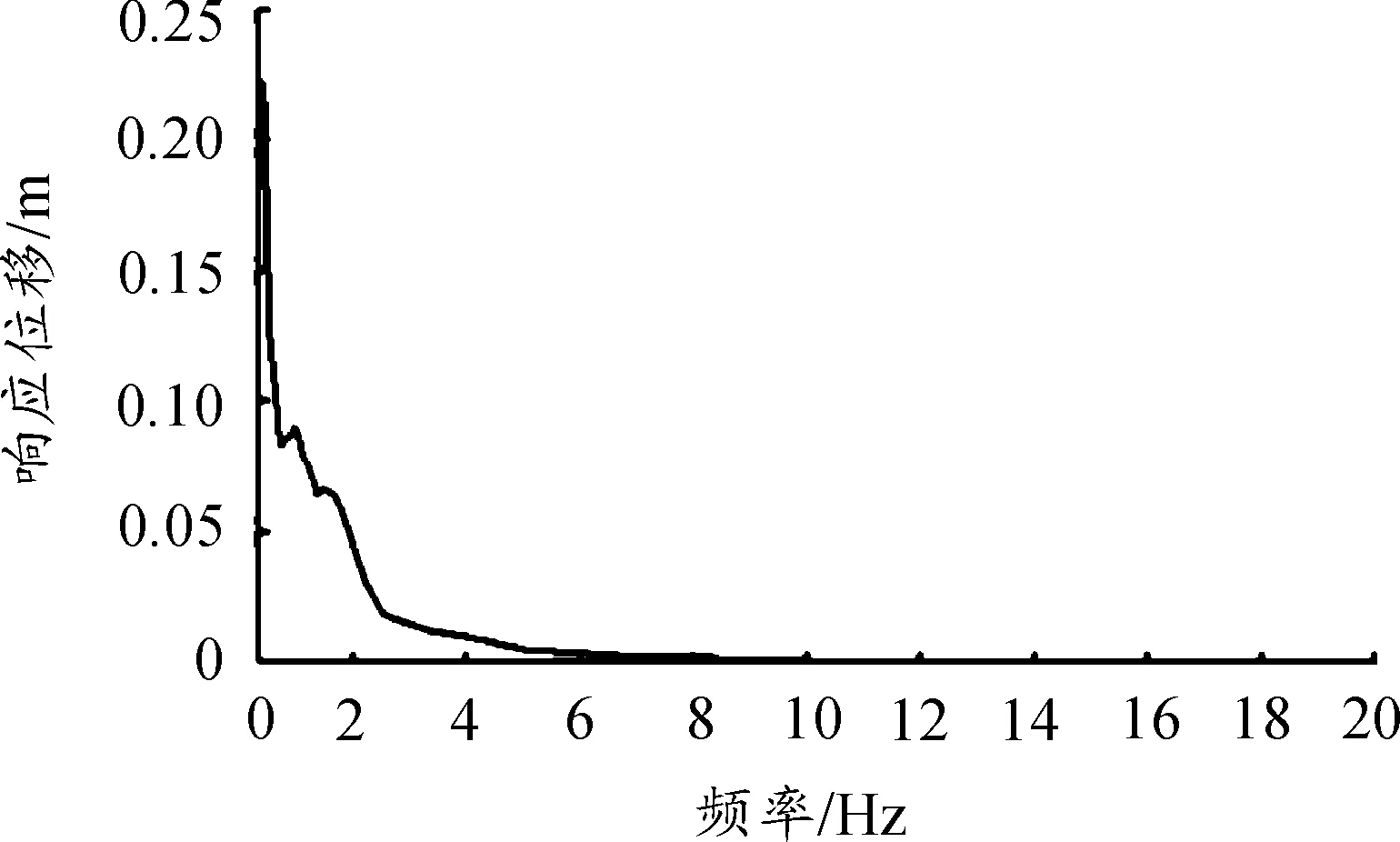
图8 响应位移频谱

Workbench中响应谱分析从频域的角度计算结构的峰值响应，即响应系数与振型的乘积[10]，振型最大响应组合在一起就给出了箭体结构的总体响应。通过Response Spectrum模块将箭体模态分析结果与地震波频谱连接计算，求解结构的应力、位移和应变等物理量[11]。

5.2 SRSS模态组合类型

在箭体模态分析的基础上，得到了前10阶振型，振型叠加目前常采用各振型平方和开方根简称SRSS的组合原则[12]。该方法建立在随机独立事件的概率统计方法之上，即要求参与数据处理的各事件之间完全相互独立，不存在耦合关联。当结构的自振形态相差较大时，近似认定各个振型相互独立。SRSS方法计算箭体结构最大位移响应公式为：

(1)

式(1)中，Wn(max)是第n个振型的最大位移响应。

同理，当计算箭体结构单元应力值时，也要首先计算各个振型的应力响应，再经过SRSS求出统计意义上的最大应力。

5.3 响应谱输入

地震波一般分解为两个水平方向和一个竖向的振动，由于三个分量不会在箭体结构上同时产生最大响应，应考虑能使结构产生最大响应的且符合实际的组合[13]，本文按照对箭体影响最大的X轴向地震波作为主方向，X向(水平NS)、Z向(水平EW)以及Y向(竖直V)地震激励按照100∶80∶50的比例加载。

加速度频谱数据加载至Response Spectrum模块，得到箭体在该频谱激励情况下的响应，X、Y、Z轴方向位移云图如图9，从上至下依次为X方向位移、Y方向位移、Z方向位移。箭体等效应力云图如图10。

在地震激励的作用下，最大位移位于X轴方向为64.601 mm，小于《运载火箭工程》[14]要求的箭体低频振动最大应变值，箭体受到的最大等效应力为238.89 MPa，主要集中在尾段发射支点处，低于材料2024-T4铝合金325 MPa的屈服强度，处于合理范围内，满足抗震强度要求。综合分析，该型火箭满足发射等待状态抗震安全性要求。

图9 箭体地震谱响应XYZ方向位移云图

图10 箭体地震谱响应等效应力云图

6 结论

模态分析方法提取箭体振型和频率，可以有效避免结构共振，优化结构特征。箭体结构通过响应谱分析方法，直观研究应力分布和位移变形，为系统工程具体操作提供数据支撑。该型火箭结构设计比较合理，应力应变分布均匀，最大应力238.89 MPa，位于尾段处，材料强度符合设计要求。绝对位移较小，不会造成箭体中轴线角度偏移。低阶模态主要为弯曲振动，高阶模态为扭转和弯扭组合，结构频率在0.1～10 Hz之间，属于低频振动范围，在7级地震波的激励下，满足抗震安全性要求。此分析方法与更为复杂的时间历程分析比较，可以更加精确地验证火箭抗震安全性能。