一种惯性测量组合陀螺常值漂移外场标定方法
阮 卫, 张秦南, 迪玉茹, 国琳娜, 王立文
一种惯性测量组合陀螺常值漂移外场标定方法
阮 卫1,2, 张秦南1, 迪玉茹1, 国琳娜1, 王立文1
(1. 中国船舶重工集团公司 第705研究所, 陕西 西安, 710077; 2. 水下信息与控制国防重点实验室, 陕西 西安, 710077)
针对惯性测量组合(IMU)外场标定问题, 文中提出一种IMU陀螺常值漂移3位置外场标定方法。在静基座条件下, 先利用二次对准技术测出产品的姿态角, 再利用卡尔曼滤波估计北向陀螺漂移, 结合3个位置的姿态角和北向陀螺漂移, 再利用最小二乘法对陀螺漂移进行求解。仿真结果表明, 该标定方法简单易行, 无需转台, 能够对陀螺常值漂移进行有效估计。
惯性测量组合; 标定; 卡尔曼滤波; 陀螺常值漂移
0 引言
惯性测量组合(inertial measuring unit, IMU)参数估计与补偿对提高惯性导航精度具有重要意义[1], 因此需要对IMU进行标定以保证其满足使用要求。然而, 随着时间的推移和环境的变化[2], 以及IMU中电子元器件的老化, 相关参数必然发生变化, 从而导致IMU指标超差, 无法满足对准和导航的使用要求。
陀螺常值漂移是IMU主要性能指标, 实航中航姿角的精度主要取决于陀螺常值漂移。文献[3]提出一种双位置陀螺常值漂移估计方法, 将加速度作为量测, 设计卡尔曼滤波器估计陀螺常值漂移, 但需要较高精度转台实现旋转。文献[4]提出一种整弹不开箱条件下IMU 7位置标定方案, 通过俯仰30°等7个小姿态特殊位置进行组件级标定, 但同样要求转台精度小于1°, 不适用于没有精密转台的现场标定。文献[5]由线性系统理论得出, 静止状态下惯导系统有6个状态变量是不可观测的。文献[6]在研究车载IMU免拆卸标定方案中, 证明陀螺常值漂移和水平加速度计零偏是可观测的。文献[7]提出二次对准技术, 对姿态矩阵连续进行2次修正, 可以解决现场存在的大失准角问题。
通过对上述文献的分析和研究, 文中提出一种IMU简易3位置标定方法, 并进行数学仿真。该方法现场仅需指北基准且允许指北基准存在较大的误差。
1 理论分析
文中导航坐标系选取北天东, 机体坐标系选取前上右, 静基座条件下惯导系统误差方程为
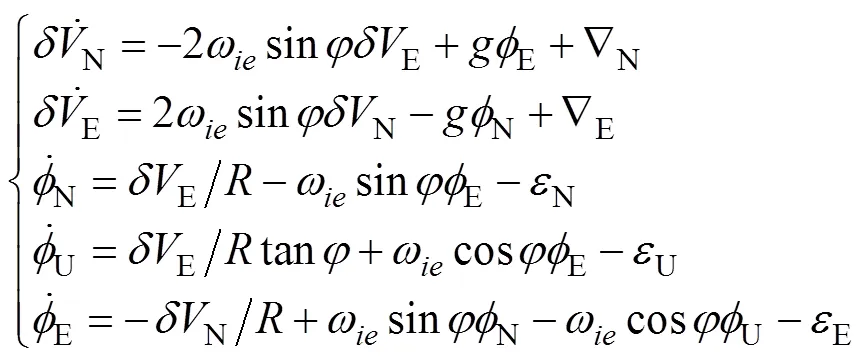

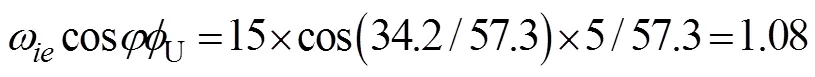
2 数学模型建立
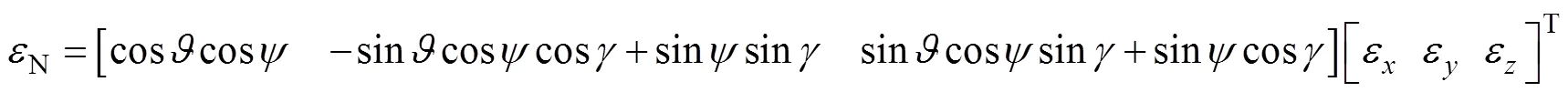
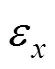
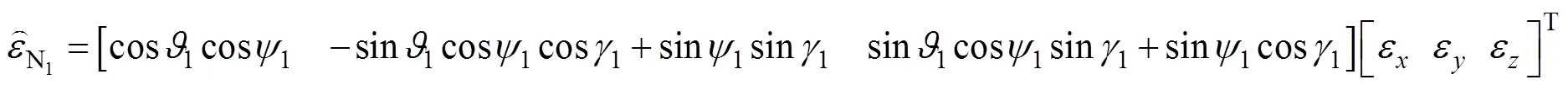

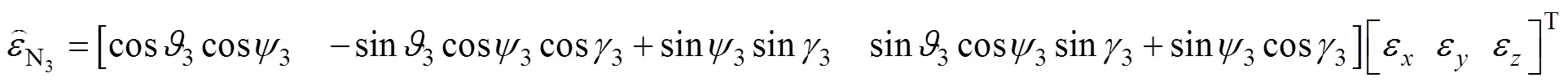
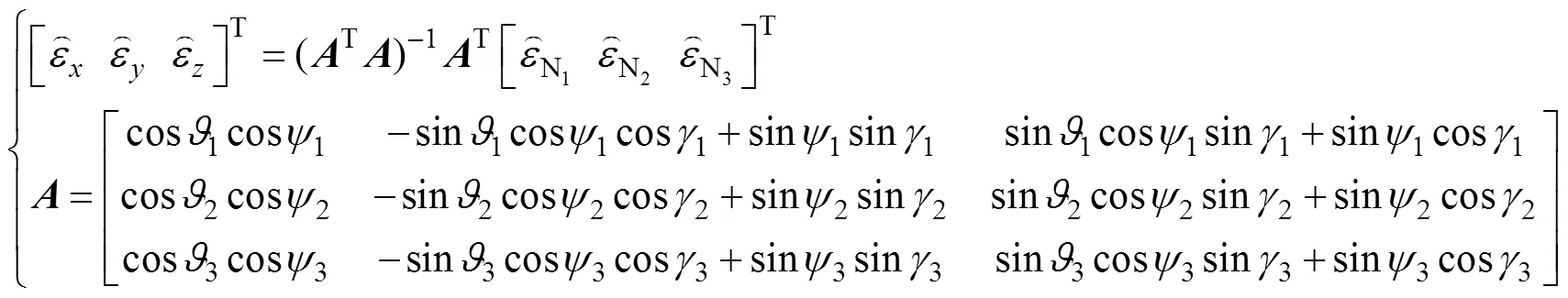
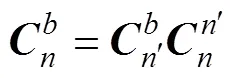
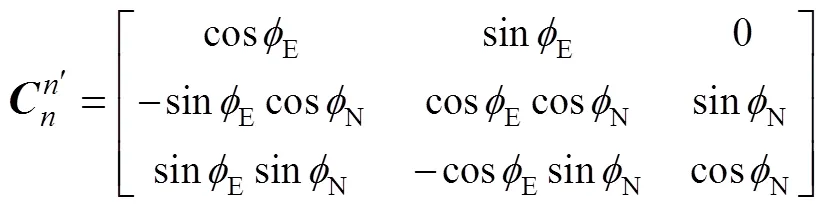
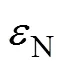
3 数学仿真
建立卡尔曼滤波方程
量测方程为

图1 3位置标定方案
IMU在位置1大概水平指北位置静止300 s生成数据; 然后大概偏航90°到位置2静止300 s;在位置2的基础大概横滚20°到位置3静止300 s。3个位置姿态角真实值如表1所示。
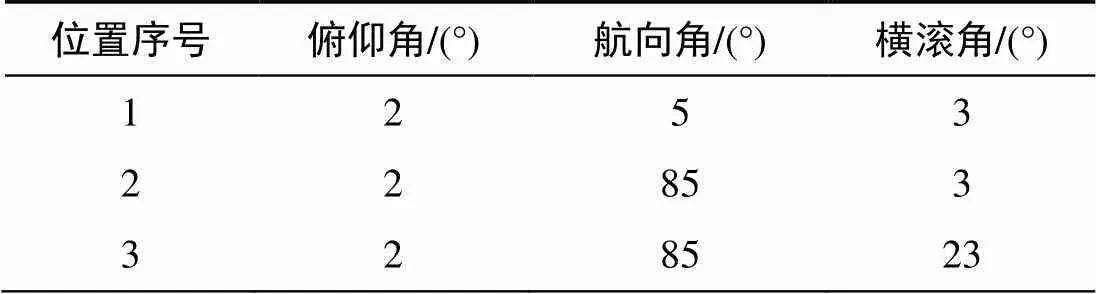
表1 3位置姿态角设置
按照编排方案生成陀螺仪和加速度计输出如图2和图3所示。
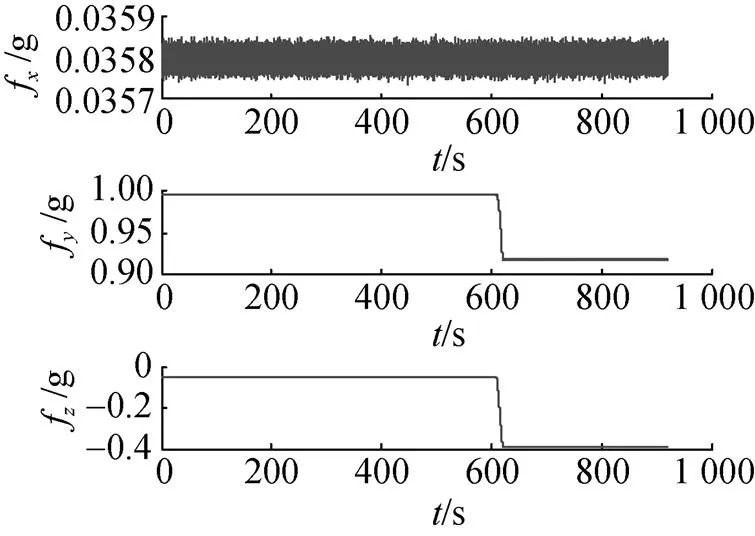
图2 陀螺仪仿真数据
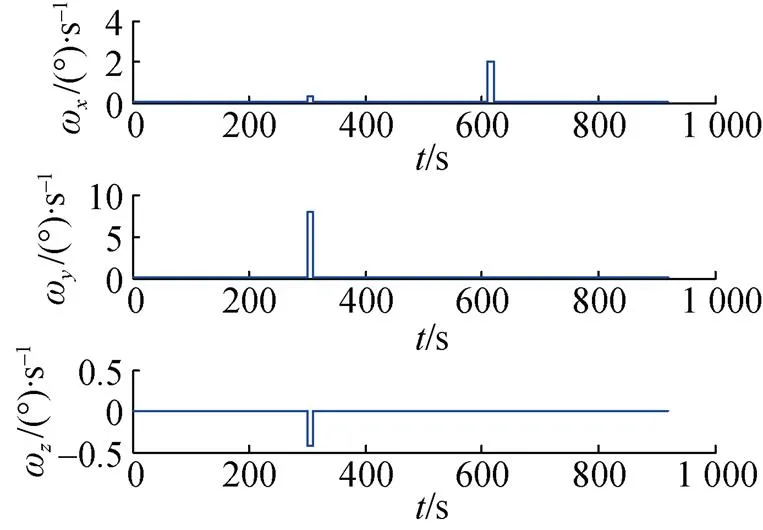
图3 加速度计仿真数据
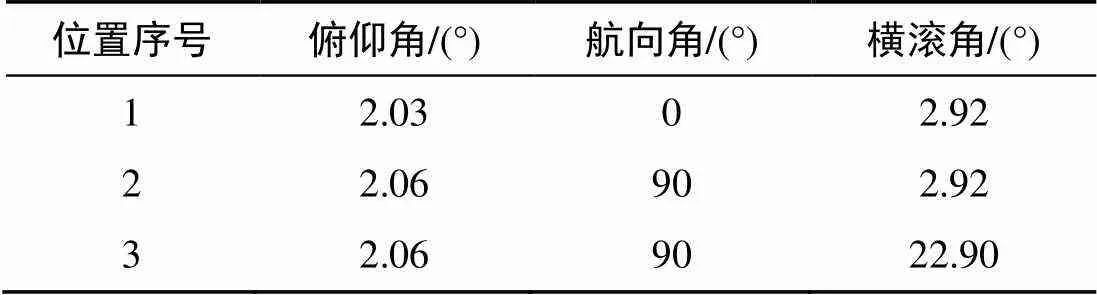
表2 3位置姿态角计算值
二次对准完成后对每个位置的北向陀螺漂移进行估计, 结果如图4所示。
每个位置具体北向陀螺漂移估计值如表3所示。
由表4可以看出, 在考虑最大5°航向角误差的情况下, 陀螺常值漂移最大绝对误差为0.06°/h, 可以满足低等精度IMU(陀螺漂移为1~10°/h)的标定要求, 从而验证3位置标定方案的正确性。
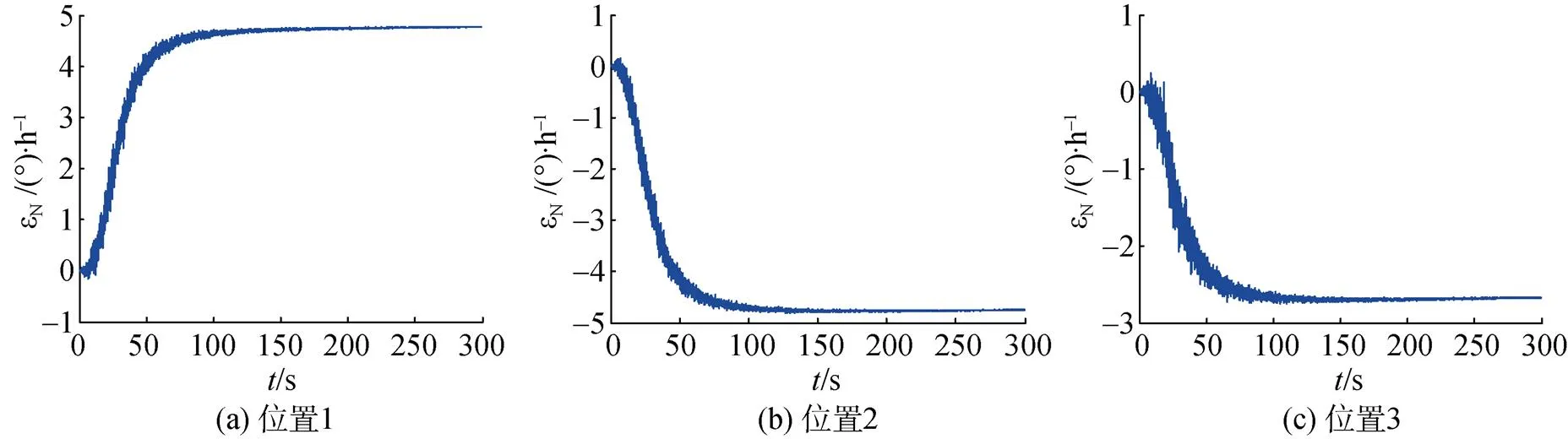
图4 3位置北向陀螺常值漂移估计曲线

表3 3位置北向陀螺常值漂移估计值

表4 陀螺常值漂移估计值与真实值对比
4 结束语
针对现场指北基准可能存在较大误差的问题, 文中提出一种IMU简易3位置标定方案, 在每一位置先利用二次对准技术对姿态矩阵进行精确修正, 再对北向陀螺漂移进行估计, 最后结合最小二乘法完成对陀螺漂移的求解。3位置标定方案与传统方法相比, 步骤简单、标定成本低, 具有重要的理论和实用价值, 可为IMU免拆卸标定提供研究思路。
[1] 杨晓霞, 黄一. 利用ESO和TD进行的激光捷联惯组误差参数外场标定方法[J]. 中国惯性技术学报, 2010, 18 (1): 1-9.Yang Xiao-xia, Huang Yi. Application of ESO and TD to Outer Field Calibration of Laser Gyro SINS[J]. Journal of Chinese Inertial Technology, 2010, 18(1): 1-9.
[2] 吴平, 雷虎民, 邵磊, 等. 一种车载筒弹惯导装置不开箱标定方法[J]. 中国惯性技术学报, 2010, 18(1): 28-32. Wu Ping, Lei Hu-min, Shao Lei, et al. Calibration without Opening Box for Vehicle Silo Missile’s Inertia Instrument[J]. Journal of Chinese Inertial Technology, 2010, 18(1): 28-32.
[3] 徐晓苏, 万德钧. 船用捷联式惯导系统初始对准及对陀螺仪随机常值漂移估计方法的研究[J]. 中国惯性技术学报, 1990(2): 17-24.Xu Xiao-su, Wan De-jun. A Study of The Methods of Initial Alignment and Estimation of Gyro’s Random Constant Drifts in Marine SINS[J]. Journal of Chinese Inertial Technology, 1990(2): 17-24.
[4] 冯志刚, 邹颖. 整弹不开箱的惯性系统射前小姿态标定方法[J]. 中国惯性技术学报, 2009, 17(1): 33-36, 41.Feng Zhi-gang, Zou Ying. Method of Small Gesture Calibration for Inertial Measurement Units without Opening Box Pre-Launch[J]. Journal of Chinese Inertial Techno- logy, 2009, 17(1): 33-36, 41.
[5] Saab S, Gunnarsson K T. Automatic Alignment and Calibration of an Inertial System[C]//Position Location and Navigation Symposium. Las Vegas, NV, USA: IEEE, 1994.
[6] 赵晓伟, 孙谦. 一种车载激光捷联惯组免拆卸标定方法[J]. 导航与控制, 2016, 15(1): 17-22.Zhao Xiao-wei, Sun Qian. A Free Disassembly Calibration Method for Strapdown Inertial Navigation System Based on the Vehicle[J]. Navigation and Control, 2016, 15(1): 17-22.
[7] 张秦南. 快速高精度的二次对准技术研究[J]. 鱼雷技术, 2001, 9(3): 33-36.
An Outer Field Calibration Method of IMU Gyro Constant Drift
RUAN Wei1,2, ZHANG Qin-nan1, DI Yu-ru1, GUO Lin-na1, WANG Li-wen1
(The 705 Research Institute, China Shipbuilding Industry Corporation, Xi’an 710077, China; Science and Technology on Underwater Information and Control Laboratory, Xi’an 710077, China)
To solve the problem of inertial measuring unit(IMU) gyro constant drift in outer field calibration, a three-position outer field calibration method of IMU gyro constant drift is proposed. Under the static pedestal condition, the attitude angles of the product are measured by the secondary alignment technique, and then the north gyro drift is estimated by Kalman filter. Finally, the gyro drift is solved by the least squares method via combining the attitude angles of the three positions with the north gyro drift. Simulation results show that this method can estimate gyro constant drift effectively without using turntable.
inertial measuring unit(IMU); calibration; Kalman filter; gyro constant drift
TJ630.33; U666.12
A
2096-3920(2019)04-0442-04
10.11993/j.issn.2096-3920.2019.04.012
阮卫, 张秦南, 迪玉茹, 等. 一种惯性测量组合陀螺常值漂移外场标定方法[J]. 水下无人系统学报, 2019, 27(4): 442-445.
2018-12-04;
2019-03-21.
阮 卫(1993-), 男, 在读硕士, 主要研究方向为水下航行器导航与控制技术.
(责任编辑: 陈 曦)

