基于双欧拉法的鱼雷空中弹道仿真

任 斌, 温志文, 杨智栋

基于双欧拉法的鱼雷空中弹道仿真

任 斌1, 温志文2, 杨智栋2

(1. 海装装备项目管理中心, 北京, 100071; 2. 中国船舶重工集团公司 第705研究所, 陕西 西安, 710077)

传统鱼雷弹道六自由度仿真多基于欧拉角方法求解运动微分方程, 可以直观地得到鱼雷的位置和姿态角。但随着鱼雷空投弹道的出现, 在倾角±90°的情况下会产生奇异点, 致使欧拉方程无法求解, 得不到正确结果。为克服上述不足, 文中采用双欧拉法建立鱼雷运动数学模型, 并对鱼雷空中弹道进行数值计算。仿真结果表明, 基于双欧拉法的弹道模型能够正确地反映鱼雷空中弹道运动规律, 在计算过程中不会因出现奇异点而发散。

鱼雷; 空中弹道; 双欧拉法

0 引言

空投鱼雷由于可以有效增加鱼雷的航程和速度, 一直以来, 都受到各国海军及相关研究机构重视[1]。而欧拉角具有概念清晰、运用实现简单的优点, 因此通常情况采用欧拉方程来描述鱼雷的六自由度运动方程[2]。

然而欧拉方程在描述鱼雷运动方程有一个致命缺陷: 在鱼雷俯仰角为±90°时, 由欧拉方程解算出来的偏航角和横滚角会出现奇异, 无法得到正确的姿态角[3]。在进行空投鱼雷研究时, 不可避免地会遇到鱼雷俯仰角为±90°的情况, 因此研究此时鱼雷姿态角的解算方法对鱼雷弹道的研究具有重要意义[4]。

航空航天领域对欧拉方程奇异性的研究较早, 也有了比较充分的认知。通常采用四元数法和双欧拉法这2种方法解决以上问题[5]。其中, 四元数法由于存在原理性缺陷, 在数值计算过程中会不断累积计算误差[6]。而双欧拉法没有原理性缺陷, 通过正、反欧拉方程的交替使用, 可有效解决单欧拉方程的奇异性问题[7], 所以得到了广泛的应用。

文中将双欧拉法引入到空投鱼雷的六自由度方程中, 以鱼雷空中弹道为研究对象, 应用双欧拉法建立鱼雷运动数学模型, 采用正反欧拉方程的交替使用, 对鱼雷空中运动规律进行有效计算分析, 为鱼雷空中弹道的研究提供支撑。

1 鱼雷运动微分方程

1.1 基于正欧拉变换的运动方程

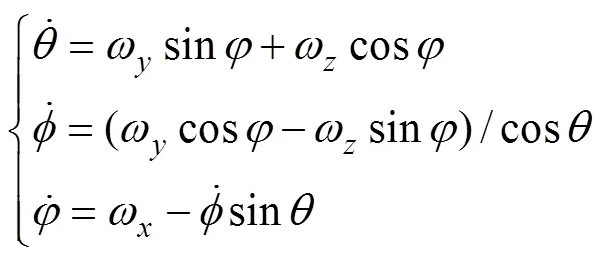
1.2 基于反欧拉变换的运动方程

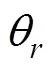
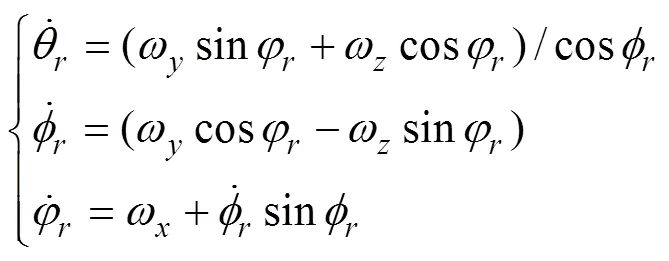
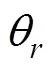
1.3 采用双欧拉法克服雷伞系统欧拉方程奇异性

由式(1)和式(3)可知, 正欧拉方程俯仰角在±90°附近, 求解出现奇异性, 在0°(和180°)位置附近, 求解比较准确。与此相反, 反欧拉方程在0°(和180°)位置附近求解出现奇异性, 在±90°附近求解比较准确[8]。那么在求解鱼雷空中运动方程时, 在±90°附近采用反欧拉方程进行计算, 在0°(和180°)位置附近采用正欧拉方程求解, 运用正反欧拉方程交替运行, 可得到比较精确的解[9]。

正反欧拉方程在交替运行时由于存在积分环节, 所以在每次计算前都需要提供初始值, 这需要通过正反欧拉方程所对应转换矩阵的坐标转换来实现。

用正欧拉角表示从地面坐标系到雷体坐标系的转换矩阵

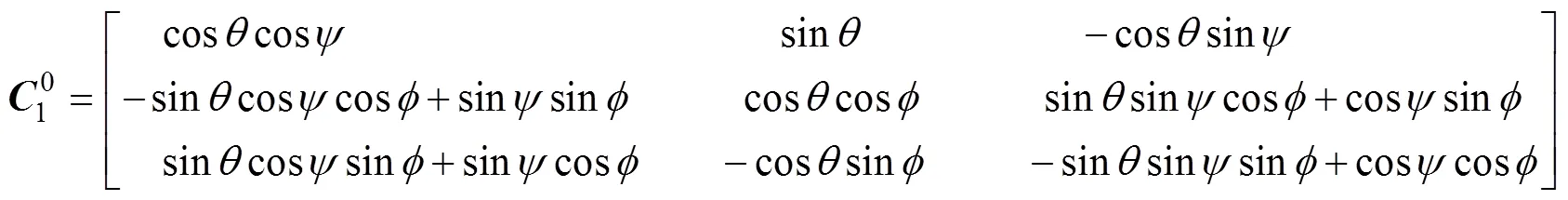
若用反欧拉角表示, 则为

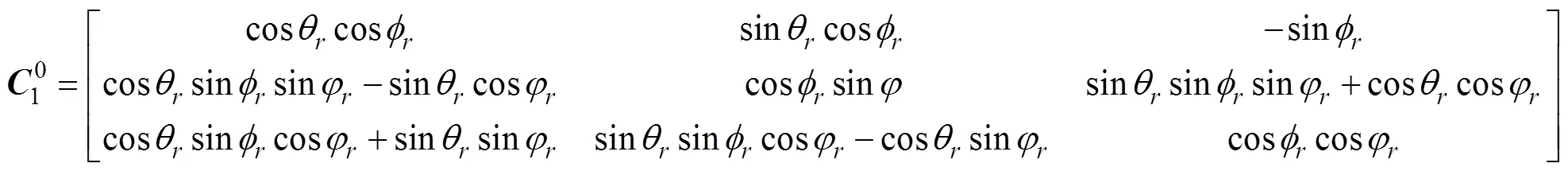
则两转换矩阵中对应元素相等, 可得正欧拉角转换为反欧拉角

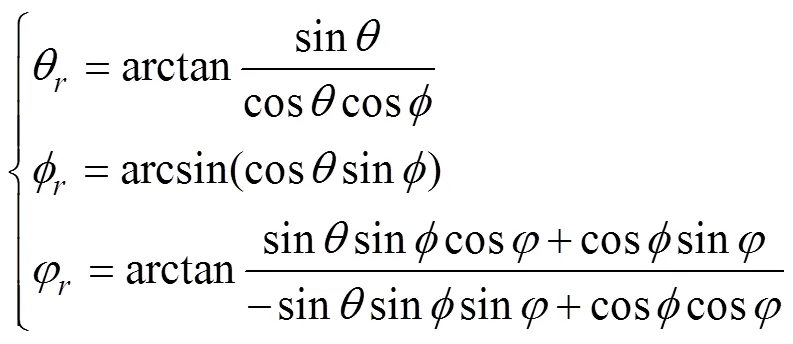
反欧拉角转换为正欧拉角

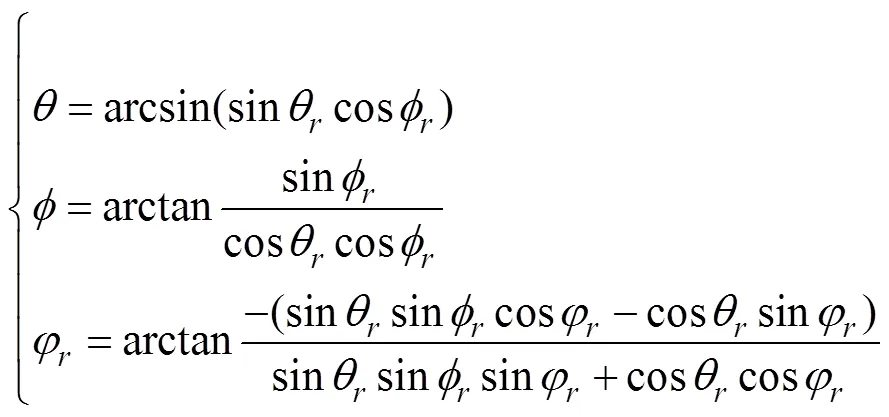
1.4 双欧拉法求解流程

双欧拉法求解流程图如图1所示。

2 仿真实例及分析

以某鱼雷空投弹道为例, 鱼雷质量10 kg, 长度1 m, 初始弹道高度500 m, 初始速度v=10 m/s,v=150 m/s, 初始俯仰角90°。利用文中双欧拉方法建立鱼雷运动数学模型, 通过仿真得到该鱼雷的空投弹道(见图2)。

图3为鱼雷轴向运动曲线, 由图可以看出, 鱼雷的下落速度在3 s后接近稳定值, 约在10 s时达到稳定状态, 速度稳定在29.4 m/s左右。图4为鱼雷俯仰角变化曲线, 由图可知, 鱼雷初始俯仰角为90°, 在降落伞的作用下翻转(降落伞绳系于雷尾)。大约在10 s时达到稳定状态, 俯仰角稳定在–89.83°左右。

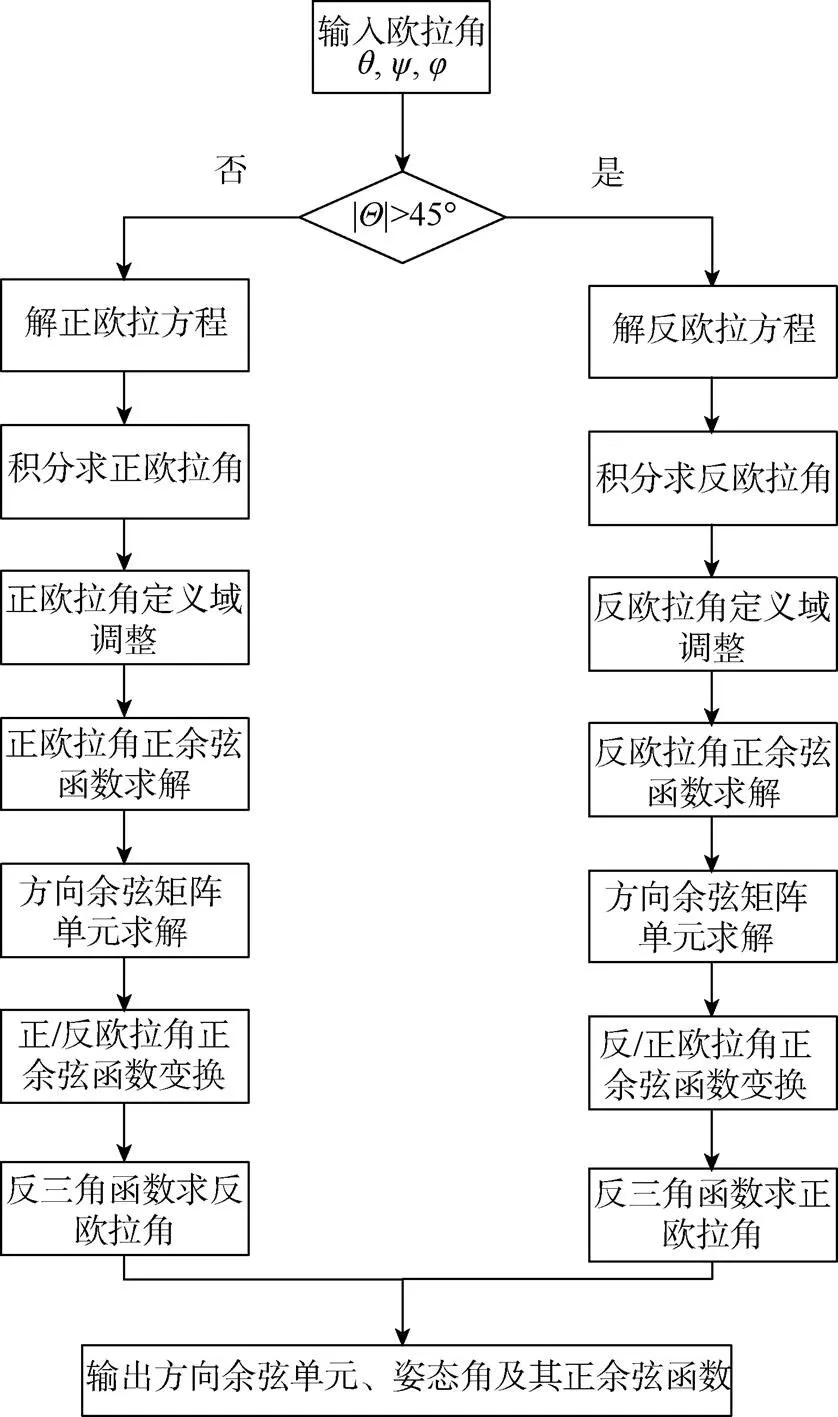
图1 双欧拉法运算流程

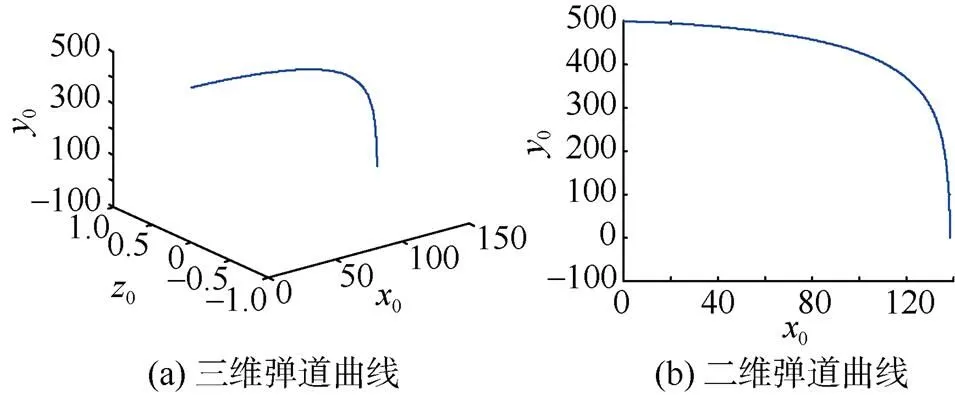
图2 空投鱼雷弹道曲线

图3 鱼雷轴向速度曲线

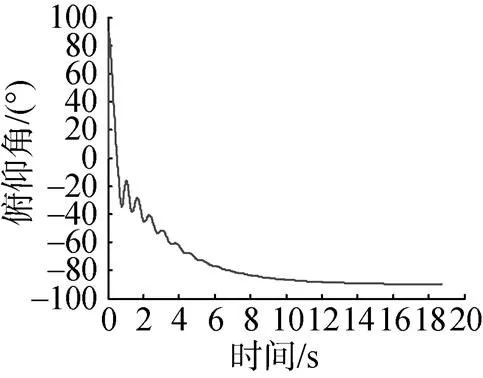
图4 鱼雷俯仰角变化曲线

由图2~图4可知, 文中采用的双欧拉法可以较好地解决空投鱼雷在俯仰角接近±90°时产生的奇异问题。

根据文中仿真结果与实际试验数据对比(见表1)可得二者能够保持一致, 证明了文中方法的可行性和准确性。

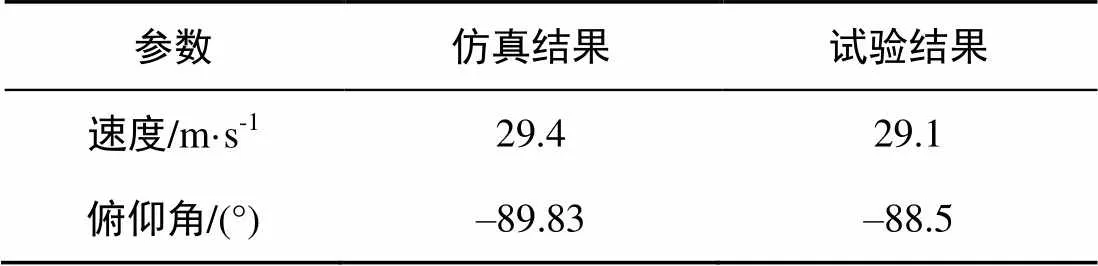
表1 文中仿真结果与实际试验结果比较

3 结束语

空投鱼雷在空中运动非常复杂, 姿态变化十分剧烈, 甚至可能发生大攻角翻转的现象。为避免这种局限性, 采用双欧拉法建立鱼雷空中运动学方程, 并在大攻角条件下进行仿真计算, 结果表明: 基于双欧拉法变换的弹道模型可正确反映空投鱼雷的运动规律, 能够仿真得到实际的弹道轨迹, 在计算过程中不会出现由于奇异点而导致方程退化的现象, 为鱼雷大幅度姿态运动的空投弹道研究提供了理论参考。

[1] 曲延明, 周明, 林宗祥. 基于Simulink的飞航式火箭助飞鱼雷空中弹道仿真[J]. 舰船科学技术, 2011, 33(12): 107-111.Qu Yan-ming, Zhou Ming, Lin Zong-xiang. Research on Air Trajectory Simulation of the Cruising Rocket Assisted Torpedo Based on Simulink[J]. Ship Science and Tech- nology, 2011, 33(12): 107-111.

[2] 李跃军, 阎超. 飞行器姿态角解算的全角度双欧拉法[J]. 北京航空航天大学学报, 2007, 33(5): 505-508.Li Yue-jun, Yan Chao. Improvement of Dual-Euler Me- thod for Full Scale Eulerian Angles Solution of Aircraft[J]. Journal of Beijing University of Aeronautics and Astro- nautics, 2007, 33(5): 505-508.

[3] 周明, 徐德民. 火箭助飞鱼雷弹道的仿真实现与应用研究[J]. 弹箭与制导学报, 2007, 27(2): 235-238.Zhou Ming, Xu De-min. Infection of Impact Dispersion to the Rocket Assisted Torpedo Detection Probability[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2007, 27(2): 235-238.

[4] 王亚东, 袁绪龙, 张宇文. 双欧控制法在运载器水弹道中的应用[J]. 鱼雷技术, 2013, 11(6): 401-405.Wang Ya-dong, Yuan Xu-long, Zhang Yu-wen. Appli- cation of Dual-Euler Control Method to Water-Trajectory Design of Missile Carrier[J]. Torpedo Technology, 2013, 11(6): 401-405.

[5] 杜阳华, 吴宇. 火箭助飞鱼雷发控及弹道仿真[J]. 指挥控制与仿真, 2014, 36(3): 89-94.Du Yang-hua, Wu Yu. Rocket-assisted Torpedo Fire Con- trol and Ballistic Trajectory Simulation[J]. Command Control & Simulation, 2014, 36(3): 89-94.

[6] 王晓娟, 唐世轩, 刘正平. 火箭助飞鱼雷系统建模与空中弹道仿真研究[J]. 弹箭与制导学报, 2003, 23(2): 51-55.Wang Xiao-juan, Tang Shi-xuan, Liu Zheng-ping. The Rocket-Assisted Torpedo System to Set Up the Mold and Air the Trajectory to Imitate the True Research[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2003, 23(2): 51-55.

[7] Jia Y, Song B W, Liang Q W, et al. Simulation of Trail Gui- dance Trajectory of a Model Torpedo Based on MATLAB/ Simulink[J]. Systems Engineering-Theory & Practice, 2006, 26(3): 141-140.

[8] 周伟, 张晓今, 寇保华, 等. 双欧拉法在克服伞-弹系统欧拉方程奇异性中的应用[J]. 航天返回与遥感, 2003, 24(3): 4-8.Zhou Wei, Zhang Xiao-jin, Kou Bao-hua, et al. The Application of the Dual-euler Method for Overcoming the Singularity of Euler Equation in Parachute-Missile System[J]. Spacecrafts Recovery & Remote Sensing, 2003, 24(3): 4-8.

[9] 岳军红, 贺怀清. 克服欧拉方程奇异性的方法[C]//第六届全国交通运输领域青年学术会议论文集. 大连: 第六届全国交通运输领域青年学术会议, 2005.

Simulation of Torpedo Air Trajectory Based on Dual-Euler Method

REN Bin1, WEN Zhi-wen2, YANG Zhi-dong2

(1. Armament Project Management Center of Naval Equipment Department, Beijing 100071, China; 2. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi’an 710077, China)

Due to its advantages of obtaining torpedo’s attitude angle and position intuitively, Euler angle representation has been extensively applied to solve the differential equation of torpedo’s six-DOF motion. However, for the torpedo air trajectory, this representation will produce singular points at the pitching angles of ± 90°, leading to the fact that the Euler equation cannot be solved. Therefore, this paper employs the dual-Euler method to avoid such singularity. Based on the dual-Euler method, a mathematical model of torpedo motion is established, and the torpedo air trajectory is numerically simulated. There is no divergence induced by the singularity during the calculation process. Simulations result shows that the torpedo air trajectory model based on the dual-Euler method can reflect the motion characteristics of torpedo air trajectory, and can achieve satisfactory performance at arbitrary angles. This work may provide a theoretical reference for the study of torpedo air trajectory.

torpedo; air trajectory; dual-Euler method

TJ631.7; O351.2

A

2096-3920(2019)04-0459-04

10.11993/j.issn.2096-3920.2019.04.015

任斌, 温志文, 杨智栋. 基于双欧拉法的鱼雷空中弹道仿真[J]. 水下无人系统学报, 2019, 27(4): 459-462.

2018-11-11;

2019-01-06.

任 斌(1982-), 男, 硕士, 主要研究方向为水中兵器装备管理.

(责任编辑: 陈 曦)