基于迭代观测更新滤波的单站无源定位算法
熊 露, 谌 剑, 毕晓文, 陈安全
基于迭代观测更新滤波的单站无源定位算法
熊 露1, 谌 剑2, 毕晓文1, 陈安全3
(1. 陆军工程大学军械士官学校 雷达系, 湖北 武汉, 430075; 2. 海军工程大学 控制科学与工程博士后科研流动站, 湖北 武汉, 430033; 3. 海军士官学校 信息与通信系, 安徽 蚌埠, 233012)
单站无源定位具有较强的隐蔽性, 能够避免多个观测平台之间数据的融合与同步等问题。针对单站无源定位算法性能易受测量误差一致性和初始状态误差等因素影响的问题, 文中从线性估计理论出发, 提出了一种基于迭代观测更新滤波(IMUF)的单站无源定位算法。首先, 将经典的一步离散线性估计器观测更新改写为连续时间上的逐步更新过程, 推导了连续逐步状态及其误差矩阵的演化方程, 然后进一步离散化得到迭代观测更新方程, 并采用Sigma点方法对其中的高斯矩进行近似计算, 得到了一种具有类似Kalman滤波运算形式, 适用于单站无源定位问题的迭代观测更新滤波算法。仿真试验证明, 较之传统算法, 该算法能够有效处理非一致性观测误差和大初始状态误差下的性能恶化问题, 在滤波收敛性与估计准确性方面更有优势。
单站无源定位; 迭代观测更新滤波; 线性估计器; Sigma点方法
0 引言
单站无源定位仅采用一个观测平台对目标进行定位跟踪, 其本身不向外辐射能量, 具有较强的隐蔽性, 避免了多个观测平台之间数据的融合与同步等问题。非线性滤波算法是单站无源定位的关键技术之一, 但由于观测模型可观测性弱, 此时观测噪声尺度差异、初始条件误差较大等原因容易导致算法定位误差增大、收敛性下降甚至估计结果发散, 因此寻求一种定位精度高、收敛速度快、性能稳定的滤波算法是单站无源定位技术需要解决的一个核心问题[1]。
经典的扩展卡尔曼滤波(extended Karman filter, EKF)算法通过对非线性方程进行1阶Taylor级数展开来逼近真实的状态分布, 当模型非线性较强时可能导致滤波性能不稳定甚至结果发散[2]。Sigma点类算法[3-4]通过采用一组确定的加权采样点来捕获高斯随机变量经过非线性变换后的均值和方差, 一方面避免了EKF在系统模型较为复杂时雅克比矩阵难于求解的问题; 另一方面其结果能够匹配到对应的真值Taylor展开项的第2阶(second order), 在适合的初始条件下相比EKF提高了高斯矩近似精度, 但在先验误差增大时则容易产生非局部采样效应(non- local sampling effect)[5-6], 导致滤波性能不稳定, 参数调谐困难[7]。此外在多传感源条件下, 当观测噪声呈现较大量级差异时将可能导致非线性条件下的高斯假设失效, 从而造成滤波性能恶化[8-10]。
针对上述问题, 文中从基本的线性估计理论出发, 将离散线性估计器一步观测更新改写为连续(伪)时间上的逐步更新过程, 推导了连续逐步状态及其误差矩阵的演化方程, 并进一步通过对其离散化后应用Sigma点矩近似方法, 得到了一种新的迭代观测更新算法。通过与经典方法的仿真对比试验表明, 迭代观测更新滤波算法能够有效处理非一致性观测误差和大初始状态误差下的性能下降问题, 具有更佳的滤波收敛性与估计准确性; 且算法实现结构与经典Kalman滤波器相似, 具有较好的可行性。
1 单站无源定位问题状态空间描述
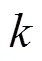

其中,

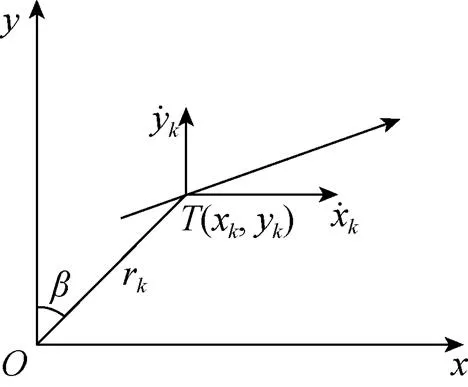
图1 观测站与目标辐射源位置关系示意图
式(1)中噪声增益项为

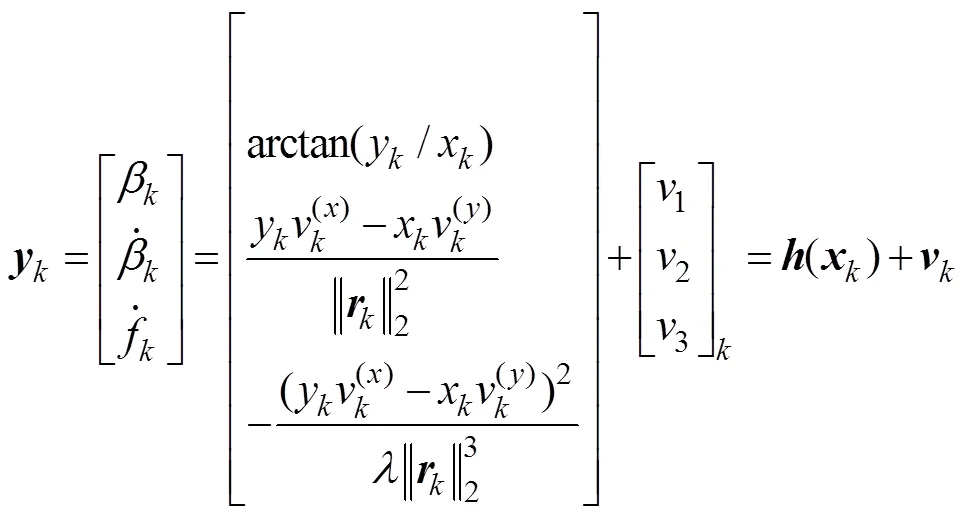
通过将跟踪问题系统抽象为基于状态空间模型描述的滤波估值问题, 即可采用滤波算法对状态进行递推估计, 从而实现实时单站无源定位。
2 迭代更新滤波算法设计
线性估计将估计值看作是观测值的线性函数, 此时问题等效为找到如下估计值

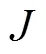
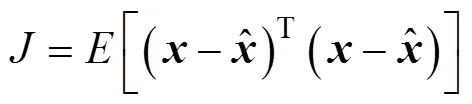
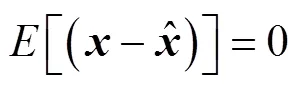
根据无偏性要求可得
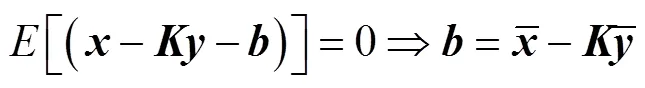
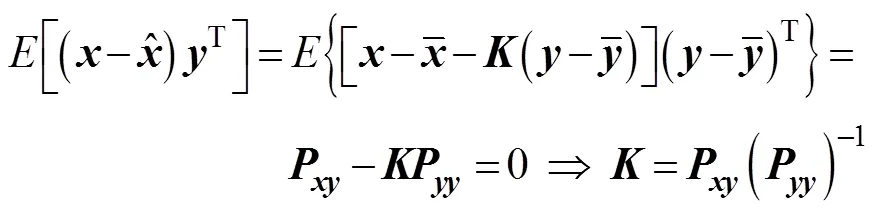
其中

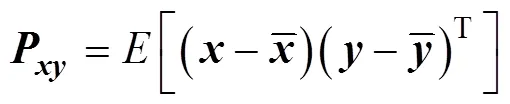
则根据式(5)可得

且可得线型最小均方差(linear minimum me- an square error, LMMSE)估计器的MSE矩阵
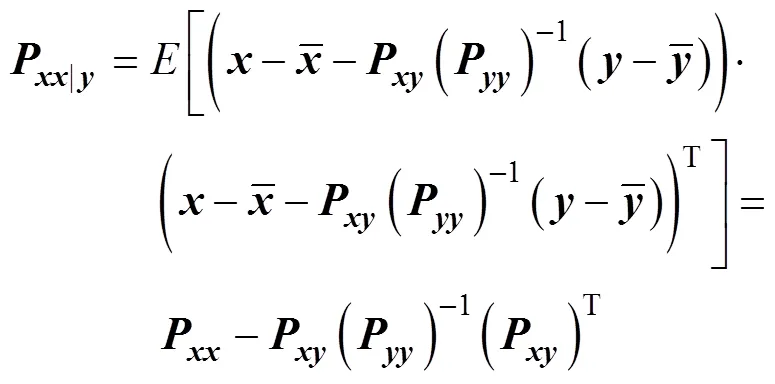
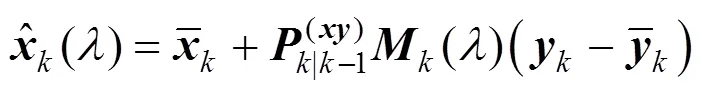
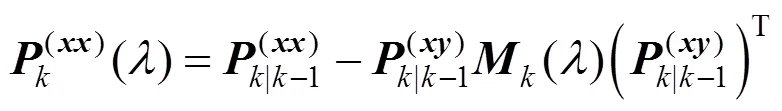
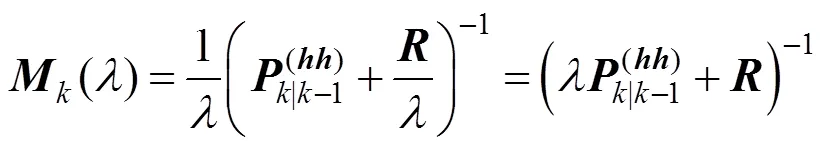
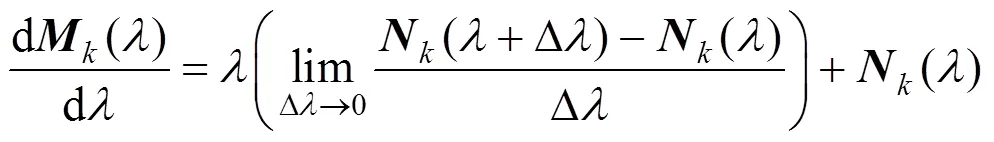

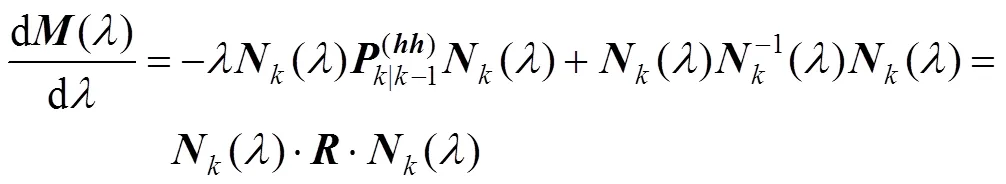
注意到对于线性估计器, 根据连续时间滤波理论[12]可近似有
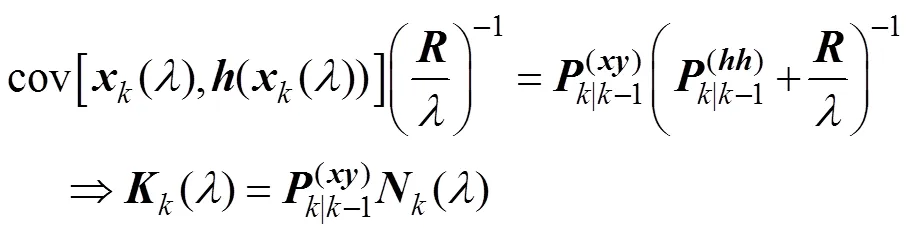
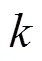
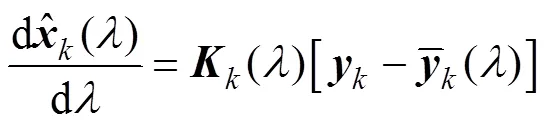
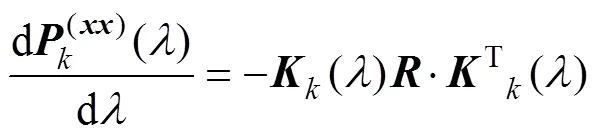
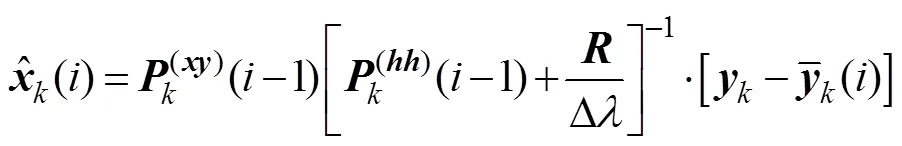

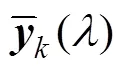
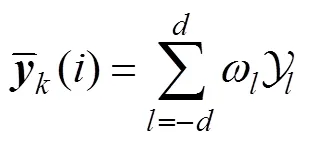

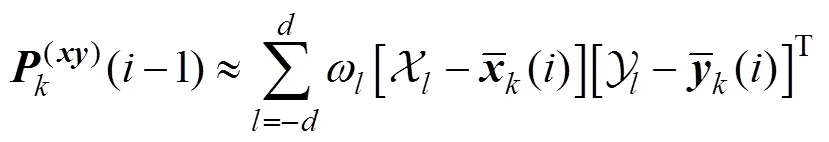
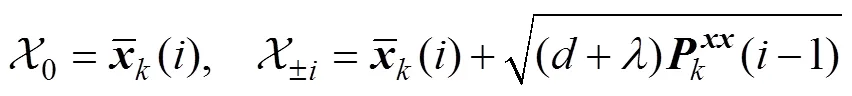
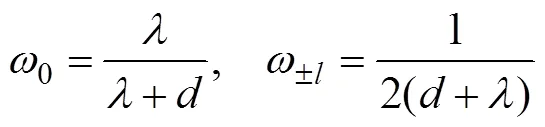

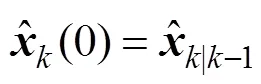
3 数值仿真与分析
为了检验 IMUF算法的性能, 将其与经典的EKF、无损卡尔曼滤波(unscented Kalman filter, UKF)以及容积卡尔曼滤波(cubature Kalman filter, CKF)算法进行计算机仿真试验, 利用这3种方法为IMUF提供滤波性能参考[14-15], 并对比所得的数值结果。
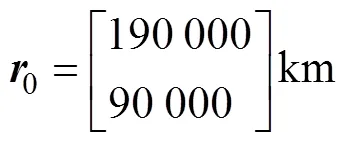
根据上述设置, 得初始状态及误差矩阵分别为
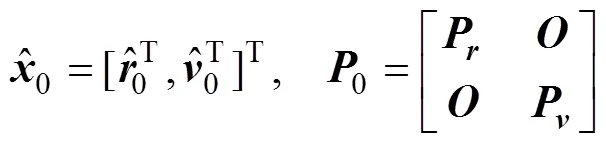
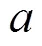
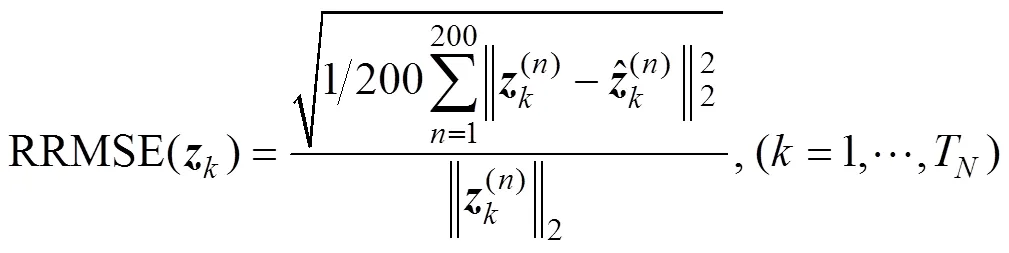
从图2中可见, 当初始条件设置与实际情况误差较小时, 文中提出的IMUF算法与UKF和CKF算法相当并略优于两者; 而从图3中则可看出, IMUF在处理大初始条件误差时能够快速收敛, 且收敛至稳定时的性能要明显优于UKF和CKF算法; 对于文中的无源定位问题, 由于实际情况中一般难以根据观测数据直接推算初始位置, 故IMUF更实用。同时可注意到, 由于观测模型具有较强的非线性, 基于1阶近似的EKF算法在2种初始误差条件下均给出了较差的估计结果。
图4~5分别给出了在状态模型中引入目标机动时, 在初始条件I和II下位置和速度估计的RRMSE, 可见目标机动对于各个滤波器的性能都造成了较大影响, 但文中算法在各个条件下均保持了良好的收敛性, 且整体误差显著低于其他几种典型方法。

图2 初始条件I下位置与速度估计相对均方根误差
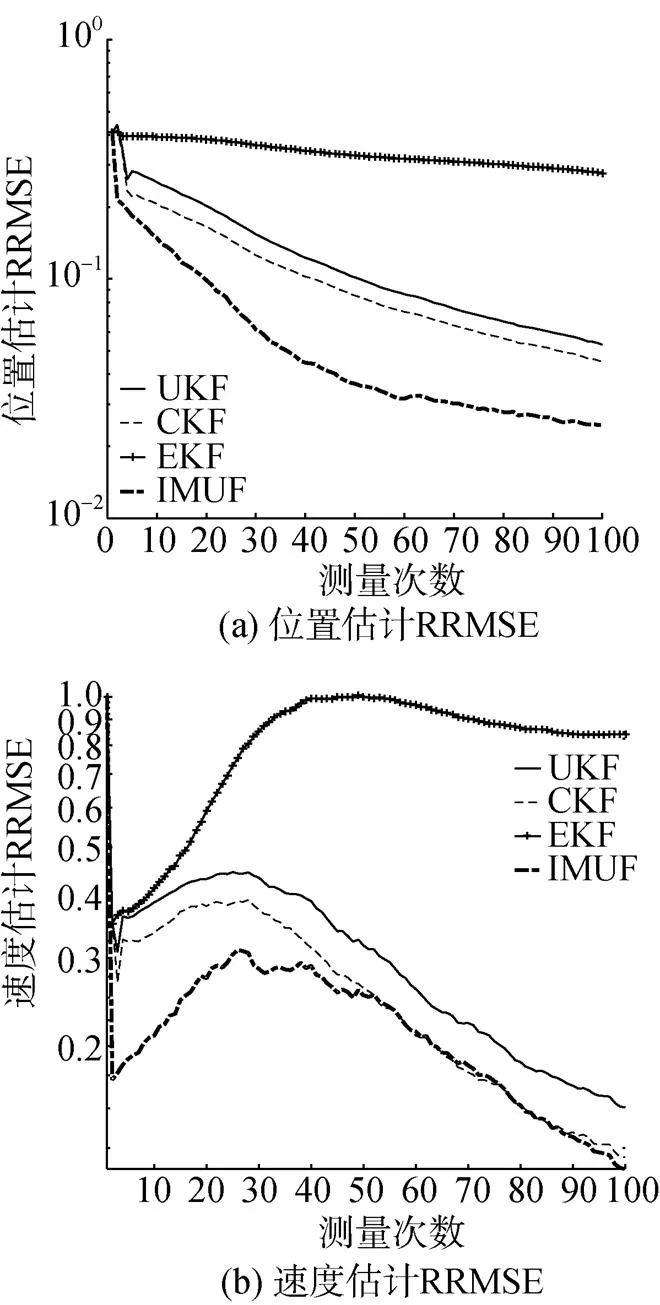
图3 初始条件II下位置与速度估计RRMSE
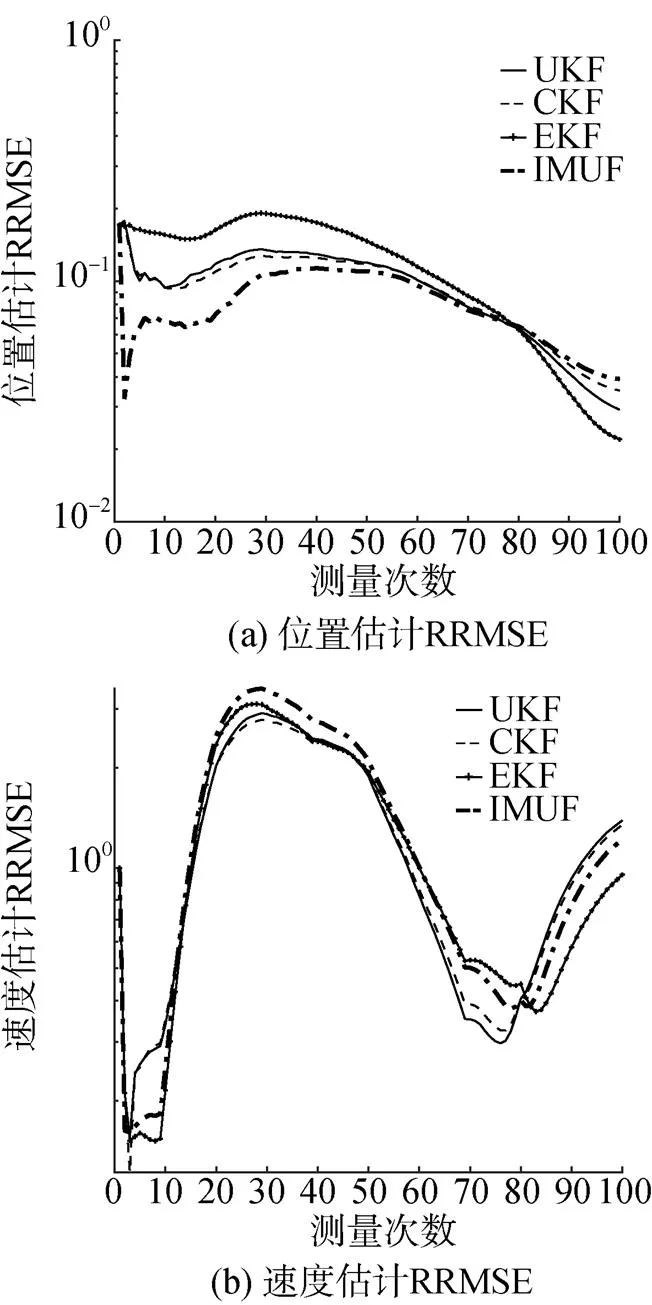
图4 目标机动时初始条件I下位置与速度估计RRMSE
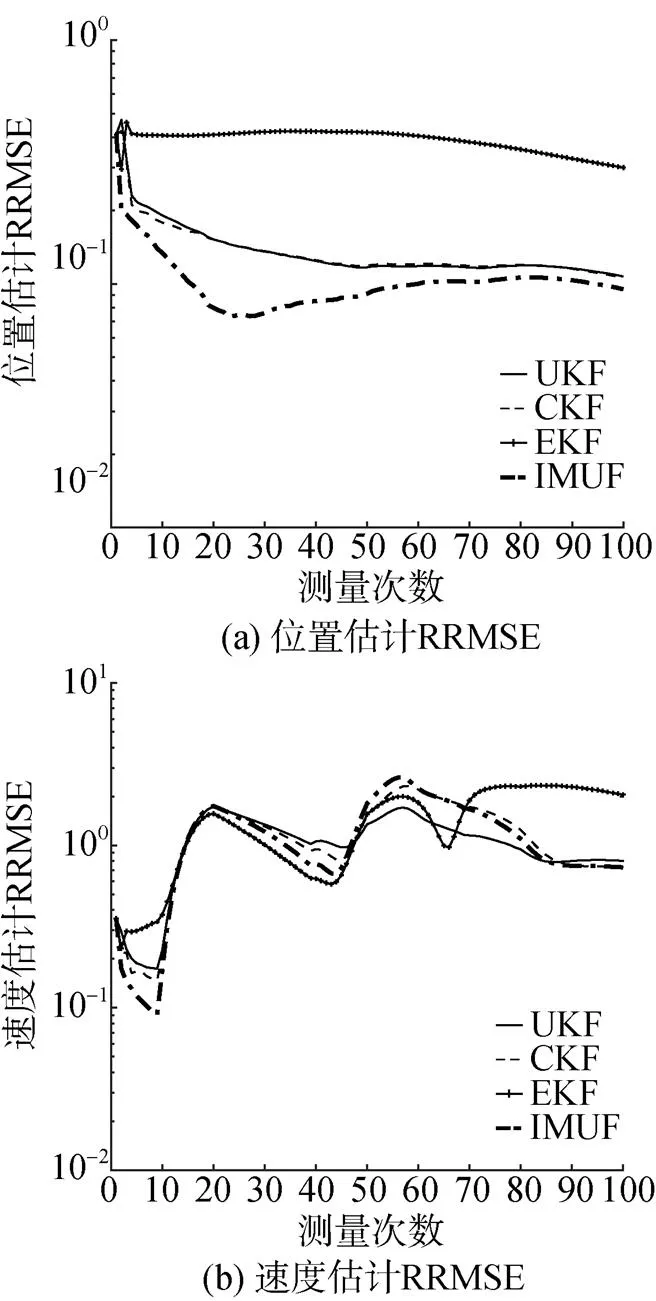
图5 目标机动时初始条件II下位置与速度估计RRMSE
4 结束语
文中提出了一种应用于单站无源跟踪的迭代观测更新滤波算法。将经典的一步离散线性估计器观测更新改写为连续时间上的逐步更新过程, 推导了连续逐步状态演化规律, 并进一步离散化得到了实用迭代观测更新算法。通过与经典方法的仿真对比试验表明, 迭代观测更新滤波算法具有更好的收敛性与稳定性, 以及更佳的滤波准确性; 且算法实现结构与经典Kalman滤波器相似, 具有较好的可行性。同时该算法也适用于其他非线性滤波领域, 对工程实践具有一定的现实意义。下一步的研究方向应集中在更为广泛的算法应用以及降低由于迭代导致的复杂度增长。
[1] 孙仲康, 郭福成, 冯道旺, 等. 单站无源定位跟踪技术[M]. 北京: 国防工业出版社, 2008.
[2] Shalom Y, Li X R, Thiagalingam K. Estimation with Applications to Tracking and Navigation[M]. New York: Wiley, 2001: 381-394.
[3] Arasaratnam I, Haykin S. Cubature Kalman Filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269.
[4] Rudolph M. Sigma-Point Kalman Filters for Probabilistic Inference in Dynamic State-Space Models[D]. Oregon: Oregon Health & Science University, 2004: 251-256.
[5] Garcia-Fernandez A F, Morelande M R, Grajal J. Truncated Unscented Kalman Filtering[J]. IEEE Transactions on Signal Processing, 2012, 60(7): 3372-3386.
[6] Chang L, Hu B, Li A, et al. Transformed Unscented Kalman Filter[J]. IEEE Transactions on Automatic Control, 2013, 58(1): 252-257.
[7] Gustafsson F, Hendeby G. Some Relations Between Extened Kalman Filter and Unscented Kalman Filter[J]. IEEE Transactions on Signal Processing, 2013, 60(2): 545-555.
[8] Zanetti R. Adaptable Recursive Update Filter[J]. Journal of Guidance Control & Dynamics, 2015, 38(7): 1-5.
[9] Perea L, How J, Breger L. Nonlinearity in Sensor Fusion: Divergence Issues in EKF, Modified Truncated SOF, and UKF[C]//Proceedings of AIAA Conference of Guidance, Navigation, and Control, South Carolina, USA: IEEE, 2007: 3489-3499.
[10] Morelande M R, Garcia-Fernandez A F. Analysis of Kalman Filter Approximations for Nonlinear Measurements[J]. IEEE Transactions on Signal Processing, 2013, 61(12): 5477-5484.
[11] 李宗华, 肖予钦, 周一宇, 等. 利用频域和空域信息的单站无源定位跟踪算法[J]. 系统工程与电子技术, 2004, 26(5): 613-616.Li Zong-hua, Xiao Yu-qing, Zhou Yi-yu, et al. Single Station Localization Algorithm for Source Free Targets Using Frequent and Spatial Information[J]. System Engineering and Electronic Technology, 2004, 26(5): 613-616.
[12] Jazwinski A. Stochastic Process and Filtering Theory[M]. New York: Academic Press, 1970.
[13] Sarkka S. On Unscented Kalman Filtering for State Estimation of Continuous-Time Nonlinear Systems[J]. IEEE Transactions on Automatic Control, 2007, 52(9): 1631- 1641.
[14] 袁罡, 陈鲸. 基于UKF的单站无源定位与跟踪算法[J]. 电子与信息学报, 2008, 30(9): 2120-2123.Yuan Gang, Chen Jing. Single Station Localization and Tracking Algorithm for Source Free Targets Based on UKF[J]. Journal of Electronics and Information, 2008, 30(9): 2120-2123.
[15] 胡振涛, 张勇, 刘先省. 基于量测迭代更新集合卡尔曼滤波的机动目标跟踪算法[J]. 控制理论与应用, 2014, 31(11): 1517-1523. Hu Zhen-tao, Zhang Yong, Liu Xian-xing. Maneuver Target Tracking Algorithm Based on Iterated Measurement Updated Ensemble Kalman Filter[J]. Control Theory & Application, 2014, 31(11): 1517-1523.
Single Observer Passive Localization Algorithm Based on Iterated Measurement Updating Filter
XIONG Lu1, SHEN Jian2, BI Xiao-wen1, CHEN An-quan3
(1. Department of Radar System, Ordnance NCO Academy of Army Engineering University of PLA, Wuhan 430075, China; 2. Post-doctoral Program on Control Science and Engineering, Naval University of Engineering, Wuhan 430033, China; 3. Department of Information & Communication, NCO Academy of PLA Navy, Bengbu 233012, China)
Single observer passive localization has strong concealment performance, and can avoid the problem of data fusion and synchronization among multiple observing platforms. To address the performance degeneration of single observer passive localization affected by the factors such as measurement error consistency and initial state error, a single observer passive localization algorithm based on iterated measurement updating filter(IMUF) is proposed in this paper. Firstly, based on the theory of linear estimation, the classical one-step discrete linear estimator update is rewritten as the step-by-step updating process in continuous time. Secondly, the evolution equations of continuous stepwise state and its error matrix are deduced and the iterated measurement updating equation is obtained by discretization. And then, the Sigma point method are used to approximate calculate the Gaussian matrix included in updating equations, and the IMUF is obtained, which has the Kalman filter-like computation form and is suitable for single observer passive localization. Finally, compared with the classical method, the experimental results show that the IMUF algorithm can effectively deal with the performance degradation problem under non-uniform measurement error and large initial state error, with better filtering convergence and estimation accuracy.
single observer passive localization; iteratedmeasurement updating filter(IMUF); linear estimator; Sigma point method
TJ630.34; TN713
A
2096-3920(2019)04-0406-07
10.11993/j.issn.2096-3920.2019.04.007
熊露,谌剑,毕晓文,等.基于迭代观测更新滤波的单站无源定位算法[J].水下无人系统学报, 2019, 27(4): 406-412.
2016-11-19;
2016-12-18.
海军工程大学科研基金(20180795); 中国博士后科学基金(2018M643864).
熊 露(1986-), 女, 博士, 讲师, 主要研究方向为目标探测与跟踪.
(责任编辑: 陈 曦)

