非自治半线性退化随机抛物方程的动力学行为

杨 潇， 李晓军

（河海大学 理学院，江苏 南京211100）

1 预备知识

考虑在DN上带有Wiener型乘积噪声的非自治半线性退化抛物方程

其中，DNRN（N≥2）是一个具有光滑边界DN的有界区域，λ 是正常数，g（t，x）∈L2loc（R；L2（DN）），ω是定义在概率空间上的双边实值 Wiener过程．非线性f∈C1（R，R），满足：

其中，l＞0，αi，βi＞0，i＝1，2．对于方程（1）中非负可测的扩散系数σ（x），σ：DN→R＋∪0，假设满足：

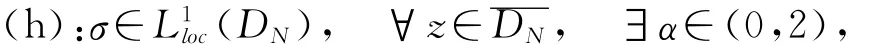
使得

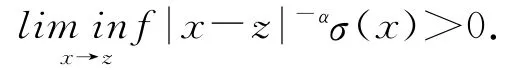
对于确定的半线性退化抛物方程的动力学已有大量的研究，如文献［1－3］．由于退化扩散系数的出现，退化抛物方程动力学行为的研究有别于传统的方法，主要表现在解的正则性估计与紧吸引集或吸收集的得到．自然界的许多现象带有随机性，带随机项的抛物方程动力学行为研究也备受关注（如文献［4－8］）．文献［4］研究了非退化带乘积噪声抛物方程随机吸引子的存在性，文献［9－10］研究了带可加噪声自治的退化抛物方程吸引子的存在性与正则性．

本文在有界域上研究带乘积噪声的非自治退化系统（1）随机吸引子的存在性．首先，通过Ornstein－Uhlenbeck变换，将方程（1）转化为一带随机参数的方程．其次，通过限制非自治项的增长和在（2）和（3）式之下，说明D－拉回吸收集的存在性．最后，通过在权空间中解的正则性估计，得到紧的吸引集．

令‖·‖和（·，·）表示在L2（DN）上的范数和内积，‖·‖p表示Lp（DN）上的范数．

1．1 函数空间 假设N≥2，α∈（0，2），令

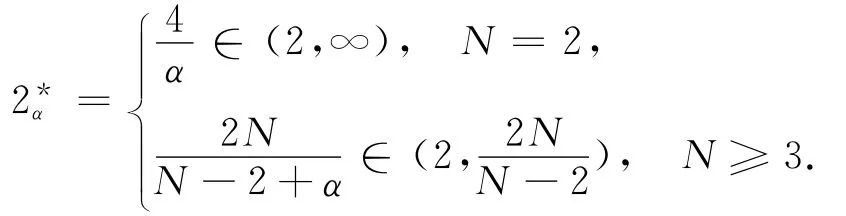
令空间D1，20（DN，σ）是C∞0按下列范数的闭包

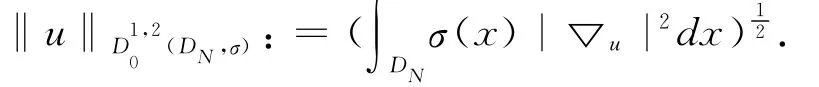
D10，2（DN，σ）上的内积定义为：

按此内积定义的空间 D10，2（DN，σ）是一个 Hilbert空间，由文献［11－12］有以下结论．

引理1．1 假设DN是RN上的有界集，N≥2，且σ满足条件（h），则有：

1）D10，2（DN，σ）L2α＊（DN）是连续的；

2）当p∈［1，2α＊）时，D10，2（DN，σ）Lp（DN）是紧的．

1．2 随机动力系统 以下叙述中关于随机动力系统的相关概念与理论，可参考文献［5－6，13］．

令Q是一个非空集，（Ω，F，P）是一个概率空间．（X，‖·‖X）是一可分的Hiblert空间，其上的Borelσ－代数为 B（X）．对任意的t∈R，σt：Q→Q是一映射，称（Q，｛σt｝t∈R）为一参数动力系统，若对任意的s、t∈R，有σs＋t＝σsοσt，σ0是Q 上的恒同映射．类似地，θ：R×Ω→Ω是（B（R）×F，F）－可测的，θ0在Ω上恒同映射，且对任意的s、t∈R，有θs＋t＝θsοθt和θtp＝p，称（Ω，F，P，｛θt｝t∈R）为度量动力系统．

定义1．2 令（Q，｛σt｝t∈R）和（Ω，F，P，｛θt｝t∈R）分别为参数动力系统和度量动力系统，映射

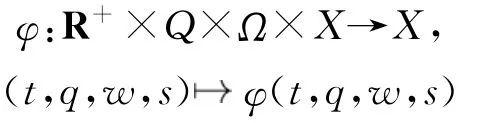
称为X 上定义在（Q，｛σt｝t∈R）和（Ω，F，P，｛θt｝t∈R）上的随机余圈，如果对于任意的q∈Q，w∈Ω和任意的s，t∈R＋，有：是可测；

（ii）φ（0，q，w，·）是X 上的恒同映射；

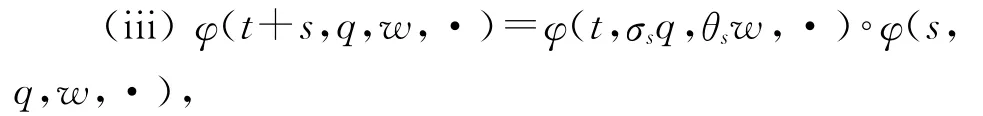
称为随机余圈φ在X中的连续余圈，如果对于任意的q∈Q，w∈Ω 和t∈R＋，φ（t，q，w，·）在X 中是连续的．

令D表示X中非空子集组成的集合

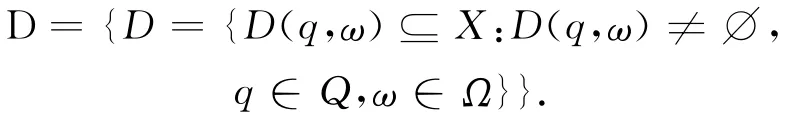
为确保拉回吸引子的唯一性，引入下面概念：称D是包含闭，若对任意的

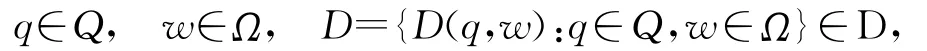
如果

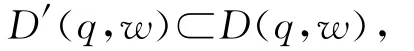
那么

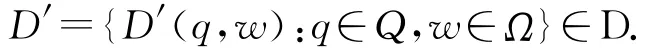
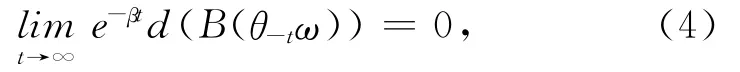
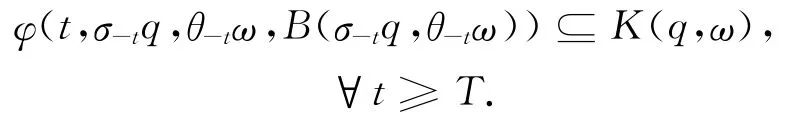
定义1．5 令D是X的非空子集族组成的集合．称φ是X上D－拉回渐近紧，如果对任意的q∈Q，ω∈Ω，当xn∈B（σ－tnq，θ－tnω），其中

且tn→∞时，序列在X中有收敛子列．

定义1．6 令A＝｛A（q，ω）：q∈Q，ω∈Ω｝∈D，称A是φ的D－拉回吸引子，如果：

（i）A关于F在Ω中是可测的，且对任意的q∈Q，ω∈Ω，A（q，ω）是紧的；

（ii）A是不变的，即对任意的q∈Q，ω∈Ω，φ（t，q，ω，A（q，ω））＝A（σtq，θtω），t≥0；（iii）A吸引D中任意集合，即

公司生技部、安监部、人资部、市场部等部门负责人，公司党校(教育培训评价中心)分管培训负责人，各地市级供电单位，云南电科院、建设分公司、带电作业分公司、送变电工程公司等分管生产和安监的相关负责人，以及各供电局县级供电企业分管生产的负责人共计80多人参加会议。

其中d（·，·）是X上的Hausdorff半距离．

定理1．7 令D是X的非空子集族组成的集合，且是包含闭的．φ 是X 上定义在（Q，｛σt｝t∈R）和（Ω，F，P，｛θt｝t∈R）上的连续余圈，则φ有唯一的 D－拉回吸引子A存在当且仅当φ在D上有一个闭可测的D－拉回吸收集

K＝｛K（q，ω）：q∈Q，ω∈Ω｝，

2 方程（1）的变换系统

下面通过Ornstein－Uhlenbeck变换将方程（1）转化为相应的含随机参数的非自治方程．

定义作用于（Ω，F，P）的群｛θt｝t∈R：

由文献［5－6，14］知，其稳定解为

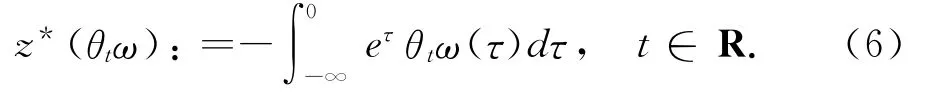
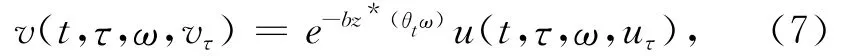
其中u是方程（1）的解，则v是

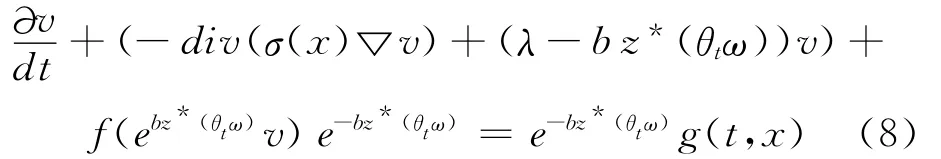
的解，其初值条件为

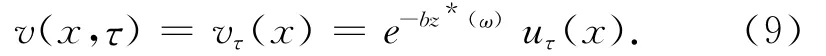
由文献［14］中引理3．1可知，e－bz＊（ω）是缓增的．设方程（1）中的λ满足

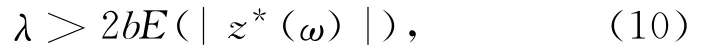
则由遍历定理［15］可知

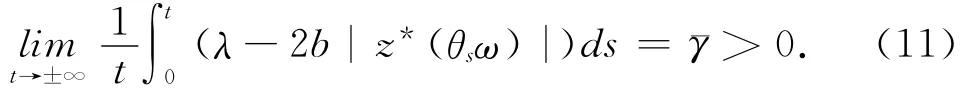
运用经典的Galerkin方法［16］可知，如果g（t，x）∈Ll2oc（R；L2（DN）），f 满足（2）和（3）式时，方程（8）和（9）在L2（DN）中存在唯一的弱解v（·，τ，ω，vτ），且对任意关于t≥τ，解关于初值vτ连续依赖．对t∈R＋，τ∈R，ω∈Ω和uτ∈L2（DN），定义

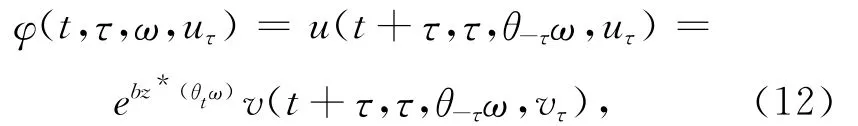
则φ是方程（1）在L2（DN）生成的连续随机余圈．令B是L2（DN）中的有界非空子集，‖B‖＝suupB‖u‖L2（DN）．假

∈设D＝｛D（τ，ω）：τ∈R，ω∈Ω｝是L2（DN）的一族有界非空子集，且满足：对任意的τ∈R，ω∈Ω，有

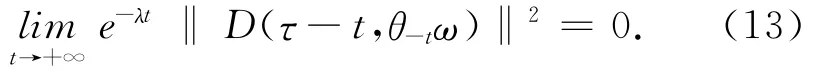
令D表示L2（DN）中满足（13）式的有界非空子集组成的集合，即

显然D是包含闭的．

对非自治外力项g（x，t），假设

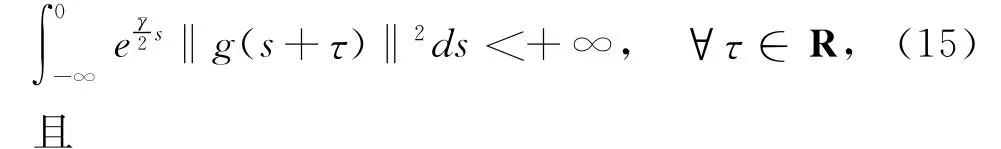
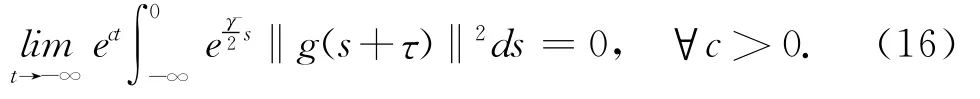
3 随机吸引子的存在性

对方程（8）的解进行一致估计，证明D－拉回吸收集的存在性和余圈φ的渐近紧性，从而得到随机吸引子的存在性．

引理3．1 假设（2）、（3）及（15）式成立，则对任意的 D＝｛D（τ，ω）：τ∈R，ω∈Ω｝∈D，存在T＝T（τ，ω，D）＞0，当t≥T 时，有

其中vτ－t∈D（τ－t，θ－τω）．

证明 将（8）式与v在L2（DN）中作内积，可得

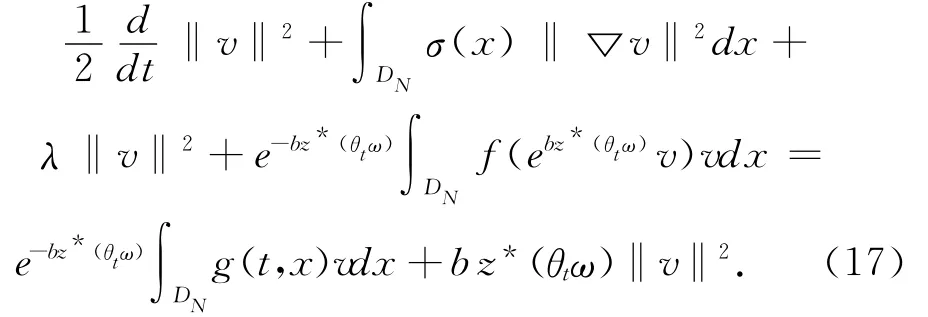
注意到，由（2）～（4）式、Hölder不等式以及Young不等式，可得：

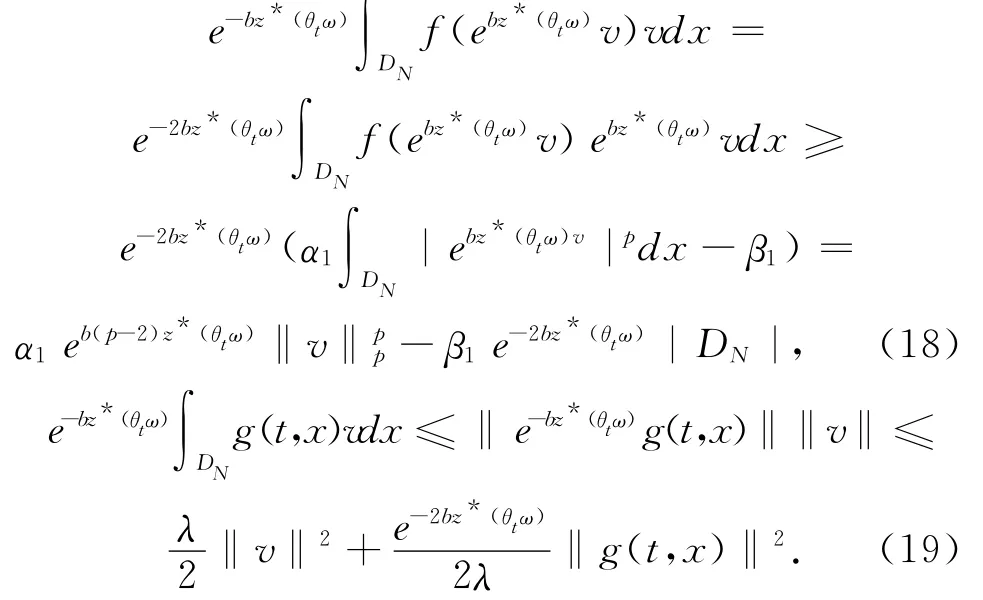
由（17）～（19）式有

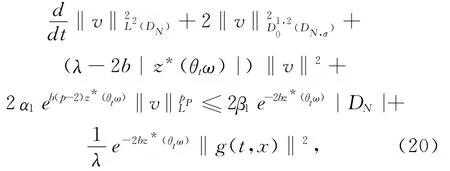
故

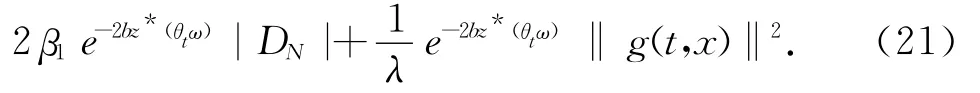
在［τ－t，τ］和t＞0对（21）式应用Gronwall引理可得

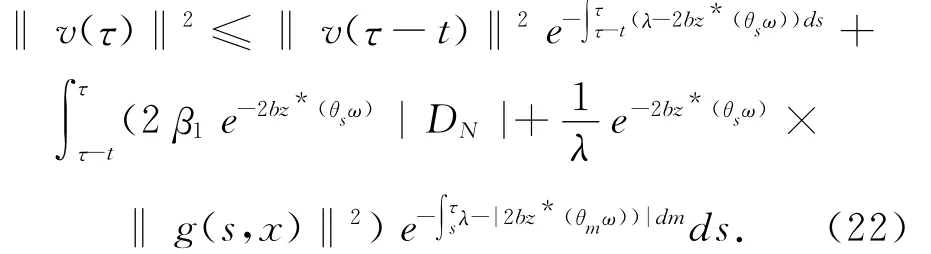
在（22）式中，用θ－τω 代替ω 得

由于e－2bz＊（θtω）是缓增的，故对任意的ε1＞0，存在T1＝T1（ε1，ω），有

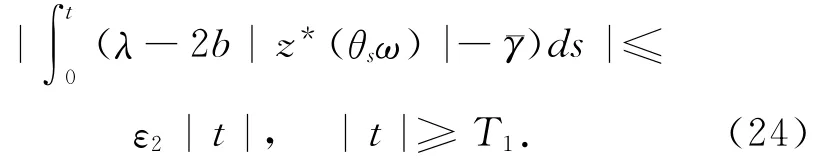
由（11）式可得，对任意的ε2，存在T2＝T2（ε2，ω），有令ε＝ε＝1γ珔，对t＞T＝max｛T，T｝，有

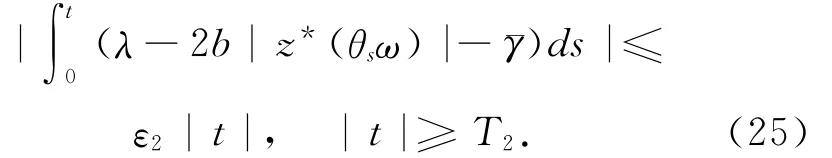
124312

应用（15）和（24）～（26）式有

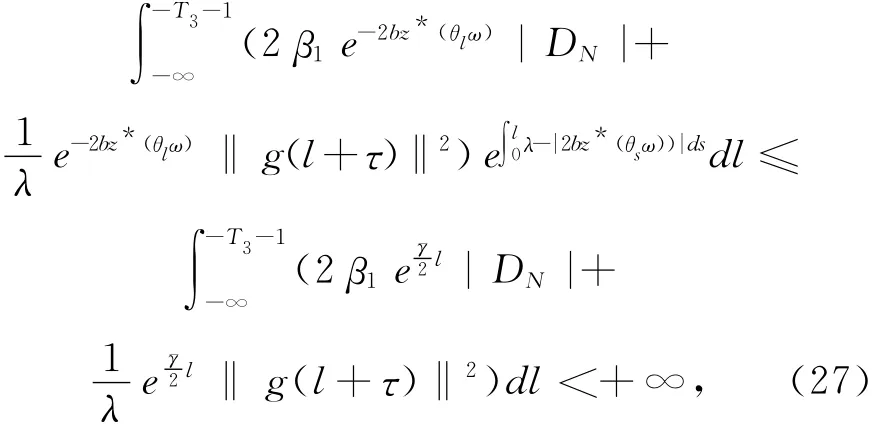
故对任意的τ∈R，ω∈Ω和D∈D，存在T＝T（τ，ω，D）＞0，使得t≥T时，有

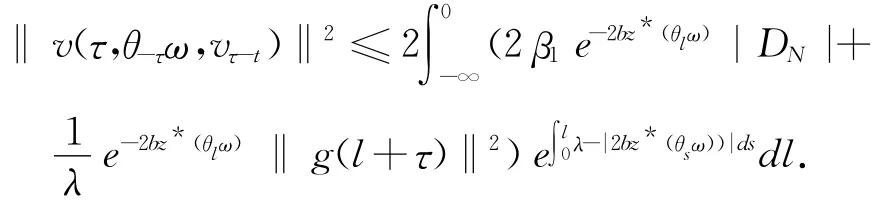
引理3．2 假设（2）、（3）和（15）式成立，则对任意的τ∈R，ω∈Ω，D＝｛D（τ，ω）：τ∈R，ω∈Ω｝∈D，存在T′＝T（τ，ω，D）≥1，使得当t≥T′时，有

其中，r＞max｛T3，T′｝．

证明 将（21）式在［0，t］，t＞0上应用 Gronwall引理，有

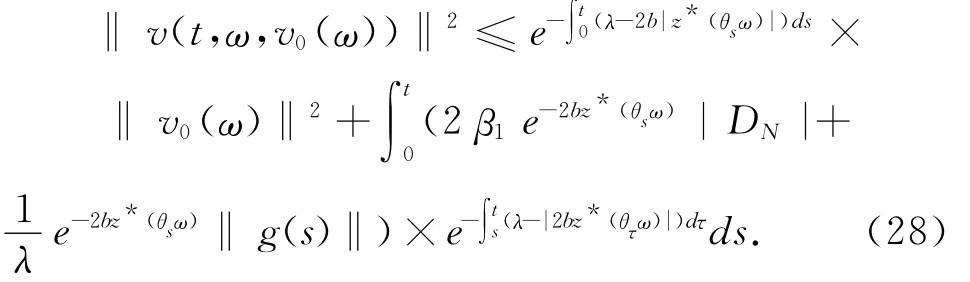
在（28）式中首先用T4代替t，T4＞T3，再用θ－tω 代替ω，有

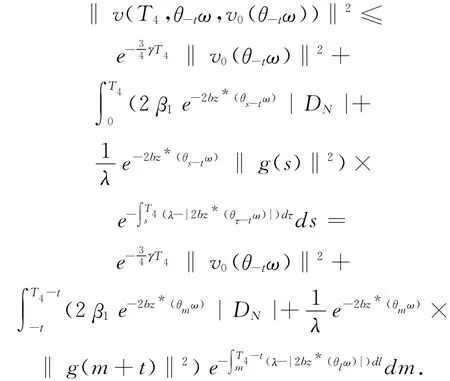
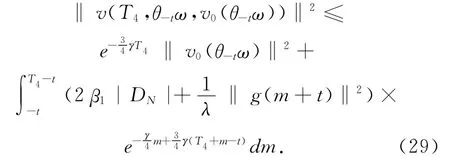
故对充分大的t，t＞T4，应用（24）式得（29）式两边同乘以e34（T4－t）γ珔得

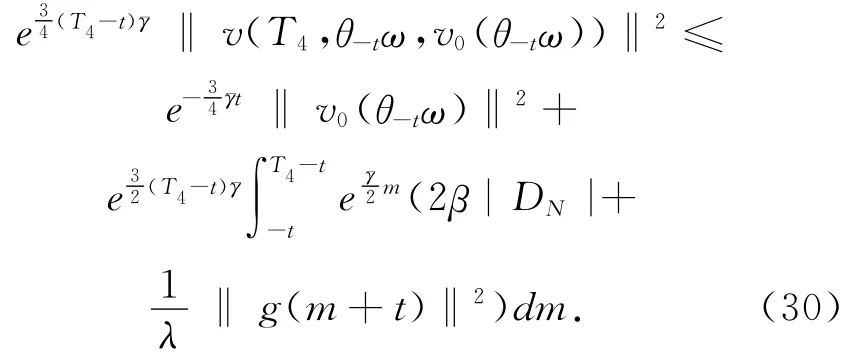
（20）式在［T4，t］上应用Gronwall引理，t＞T4＋T3，用θ－tω 代替ω 并应用（30）式得

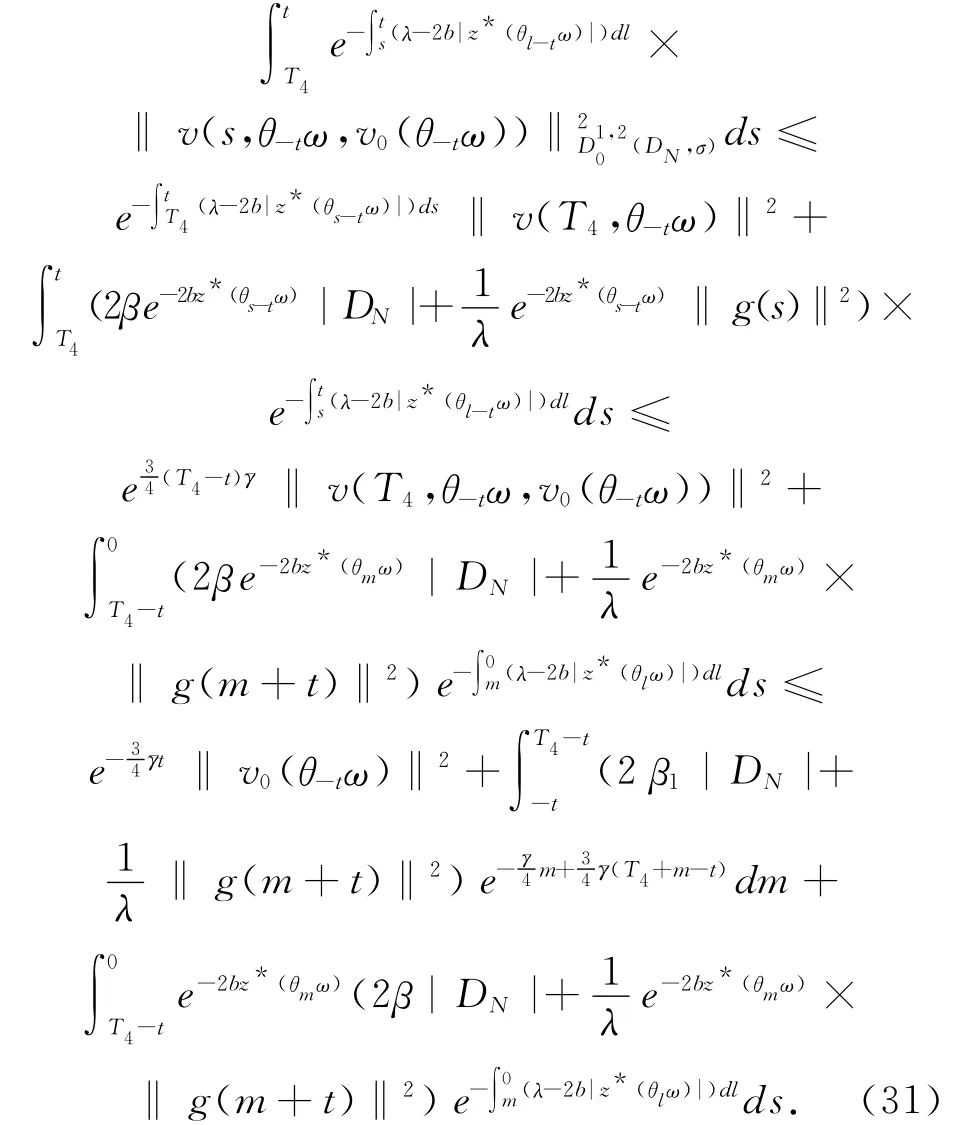
在（31）式中，用t代替T4，t＋r代替t，其中r＞T3，有

注意到，对t≤s≤t＋r，有

由于‖v0（θ－t－rω）‖2是缓增的，故存在T′（D，ω）＞0，当r＞max｛T3，T′｝，由（32）和（33）式可得

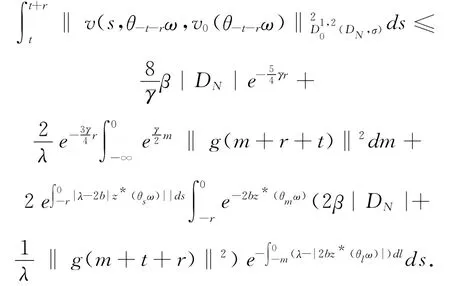
引理3．3 假设（2）、（3）和（15）式成立，则对任意的τ∈R，ω∈Ω，D＝｛D（τ，ω）：τ∈R，ω∈Ω｝∈D，存在T″＝T″（τ，ω，D）≥1，使得当t≥T″时，有

证明 将（8）式与 Av＝－div（σ（x）▽v）在L2（DN）中作内积，有

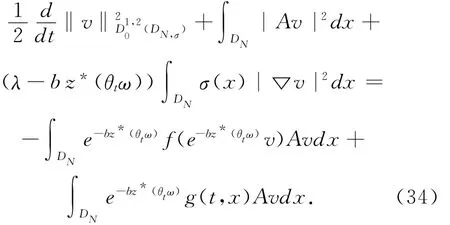
注意到

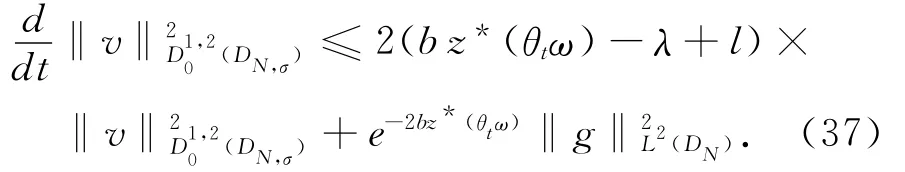
由（34）～（36）式可得取t≥T′，且s∈（t，t＋r），这里T′与r同引理3．2，对（37）式在（s，t＋r）上积分，有

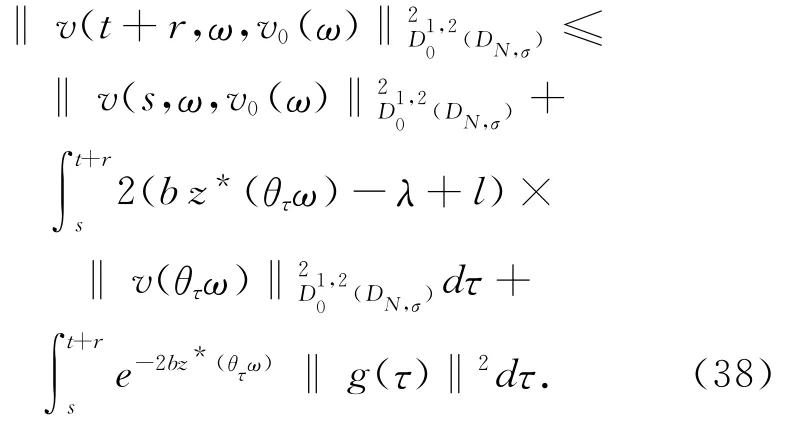
用θ－t－rω 代替ω 有

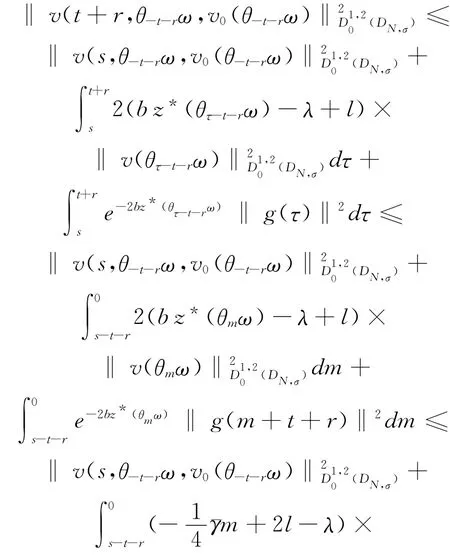
对（39）式中s在（s，t＋r）上积分有

由引理3．2可得

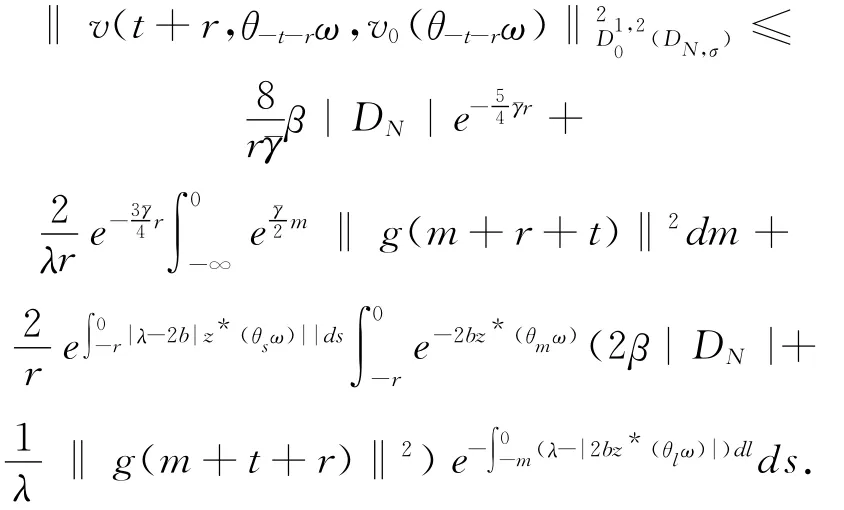
至此，有下面主要结果．

定理3．4 假设（2）、（3）、（8）和（9）式成立，则由系统（1）生成的随机动力系统φ于L2（DN）上存在唯一的随机吸引子A．

证明 由引理3．1可知，在假设（8）和（9）成立下，φ于L2（DN）中存在缓增的拉回吸收集．由引理3．3可知，φ是拉回渐近紧的，故应用定理1．7，结论成立．