参考答案略粗放,推理计算实集约
——基于2018年中考宜昌数学卷第24题参考答案的思考
☉湖北省姊归县教育科研信息中心 何训光
☉湖北省姊归县归州镇初级中学 叶先玖
2018年中考数学宜昌卷第24题,整合了初中阶段的一次函数、反比例函数和二次函数,守住《义务教育数学课程标准(2011年版)》的底线,题不超标,解却有道,直击数学学习的灵魂.解答这道题,会自觉地对题中蕴含的基本数学思想和方法进行吸收和内化,会获得真正受益终身的宝贵财富.下面就此题的解法探究、笔者的思考和获得的启示等方面做一全面分析,以期得到专家和学者的指点和帮助.
一、原题呈现

图1
题目:如图1,在平面直角坐标系中,矩形OADB的顶点A、B的坐标分别为(-6,0)、(0,4),过点C(-6,1)的双曲线y=(k≠0)与矩形OADB的边BD交于点E.
(1)填空:OA=___________,k=___________,点E的坐标为___________.
③当点F和点P随着t的变化同时向上运动时,求t的取值范围,并求在运动过程中直线MN在四边形OAEB中扫过的面积.
二、试题赏析
试题聚焦核心素养,注重通性、通法,立意新颖、巧妙,富含数学思维,解法思路多样,具有一定的创新性、前瞻性和导向性,导向明确,思维求活,育人求实.
在考查方向上,注重体现核心基础知识和数学思维品质的特点,突出对数学运算与逻辑推理的考查.
在考查内容上,传承本地对含参函数问题的研究,延续定轴动区间或动轴定区间函数命题风格,侧重于在平面直角坐标系内综合考虑点、直线、双曲线、抛物线的运动变化及相对位置关系,考虑特定情形下的公共点、临界点及面积情况,再充分借助几何直观,考查学生的逻辑推理、数学运算和直观想象素养.
在命题技术上,隐去不必要的图形,设置合理坡度以搭建“脚手架”,体现命题者对考生的人文关怀,关联通法与巧法,求实而不失科学、严谨,有层次地考查学生应对复杂情境中工作的要求并成功开展工作的综合能力及关键能力.
三、解法展示
1.命题教师给出的参考答案,以下简称“解法1”
解:(1)填空:OA=6,k=-6,点E的坐标为
(2)①设直线MN:y=k1x+b1.
当1≤t≤6时,yp随着t的增大而增大,此时,当1≤t≤6时,随着t的增大,点P在直线x=-1上向上运动.
当1≤t≤4时,yF随着t的增大而增大,此时,随着t的增大点F沿着y轴向上运动,则1≤t≤4.
当t=1时,直线MN:y=x+3与x轴交于点F(-3,0),与y轴交于点G(0,3).
命题组发布试题评述时这样表述道:“第24题侧重于在平面直角坐标系内综合考虑点、直线、双曲线、抛物线的运动变化及相对位置关系,考虑特定情形下的公共点、临界点及面积情况,在充分借助几何直观的理解下,综合考查学生的逻辑推理、数学运算和直观想象素养.”不难发现,命题组给出的参考答案,解法简洁,力求多思少算,倡导多想少写,不失人文关怀.但是,笔者在自行解答后,再与答案比对时,发现参考答案第(2)问②和③留下的思考空间似乎大了点.
2.参考答案中的部分困惑
对于第(2)问的②,参考答案借助运动变化观念,进行直观推理,临界分析得出或时,抛物线与矩形OADB有且只有三个公共点.这个解答的结论完全正确,但笔者困惑的是:这种解法是否严谨?特定情形下的临界分析,特情处理能否取代逻辑推理?要不要在解后进行验算去进一步推理?有没有基于课标要求学生能进行严谨推理的解法?
对于第(2)问的③“当t=1时,直线MN:y=x+3与x轴交于点F(-3,0),与y轴交于点G(0,3),当t=4-时,直线MN在四边形AEBO中扫过的面积为”,显然是在运动变化观念下的临界分析,但这里,如果不自行解答,为什么会出现?对于直线MN在四边形OAEB中扫过的面积,其临界点在什么地方,以及为什么会在这个地方?基于几何直观和割补法求MN扫过的面积,还有没有其他不同的解法?
3.解法再探

图2
下面呈现笔者一部分粗浅的思路,以期能解决上述解答困惑.
解法2:(2)①分别过点M、N作坐标轴的平行线,如图2.由k的几何意义及纵横比,得再把点M或N的坐标代入y=x+b1,求出直线的解析式从而避开繁杂运算,后边解答过程同解法1.
情形1:当抛物线过点B时,由对称性知抛物线与BD有另一个交点(-2,4),则,解得.抛物线此时必与AD相交于点M.又点M的横坐标为-6,则点M的纵坐标为0,此时点M在DA的延长线上.此时,令y=0,得x+4,解得x=2或x=-4,即抛物线与x轴有两个交点为(2,0)或(-4,0),故此时抛物线与矩形有三个交点,如图3,即点B(0,4)(-2,4)及(-4,0),故符合题意.

图3

图4
情形2:当P不过点B时,要使抛物线与矩形OADB有且只有三个公共点,则必定有点P在DB上,如图4.由抛物线的对称性,可知:抛物线右侧必与线段BO相交,其左侧必与线段AD相交或有一个交点在线段AO上,则=4,解得当时,有,抛物线与线段OB交于点,与线段DB交于点(-1,4),与线段AD交于点).此时,令y=0,得,解,即抛物线与x轴有两个交点,但这两个交点有一个在线段AO上,故此时抛物线得与矩形有三个交点,即故符合题意.
③与解法1过程相同,可求得1≤t≤4.
对于直线MN扫过的面积,笔者猜测考生可能会得到以下五种不同解法:
解法1:当t=1时,直线MN的解析式为y=x+3,它与x轴交于点F(-3,0),与y轴交于点G(0,3).
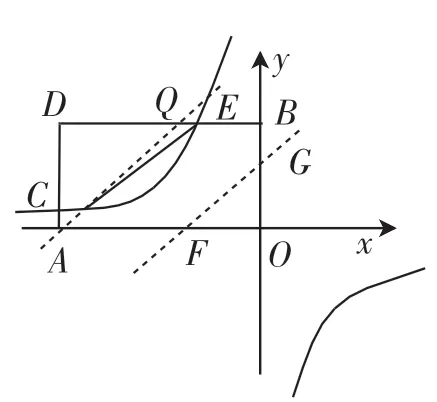
图5
解法2:过点A且平行于直线MN的直线的解析式为y=x+6,设它与BD的交点为Q(-2,4),S=S梯形AOBQ-S△AEQ-
解法3:连接AB,同解法1证明时,直线MN落在四边形AOBE外,所以当1≤t≤4时,直线MN在四边形AEBO中扫过的面积
解法4:连接EF.
解法5:
四、教学启示
笔者认为,面对思维跨度大的参考答案,或者面对那些要求直接写出答案的中考压轴题,命题者应当智慧地带来以下两点教学启示:
1.必须明确数学学科核心素养的内容
数学学科核心素养,说到底是立德树人的落实,即利用数学文化、知识等素材,在传承中发挥数学的育人功能和价值,培养学生良好的品质和习惯等;通过数学学科知识素养的学习与提升,形成用数学眼光处理问题的方法策略的素养和能力,学会交流、学会遵守规则、学会表达与合作,即“用数学眼光观察世界,用数学思维分析世界,用数学语言表达世界”.
从以上解答分析可看出,跨度较大的解答背后,却指向本地今后函数题的教学,应当在数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识和创新意识等方面用足力量,落细、落实初中生应当具备的数学学科核心素养.
2.必须明确掌握必要的数学技巧
一是要学会画一画.要在解题过程中学会画草图.学会画图,可以给学生想象的空间,感悟解决问题的方法,厘清解决问题的思路,这从解法1、解法2中可以看出,补画草图,观察直线MN与抛物线的运动变化趋势,联立解析式,着眼交轨法,从而采用临界分析,进行特情处理,而这种解法正好是命题人文关怀给予答题者的暗示,与命题意图相吻合.思维与严谨是数学学科必备的核心素养之一,也是本题给出的教学导向.教学时,直观和想象不能取代计算与推理,推理与计算必须同行,补图与验算必须同进,直观与想象必须并列,合情与严谨必须并存.否则,以形表数时,当出现思维定式导致画图分析不全面时,往往会出现错解或漏解.
“逻辑推理是数学的命根子”“数学运算是数学的童子功”.推理与计算是初中数学的硬功.数学教学,素养优先于模型,核心优先于刷题.一味刷题,过度重视模型、套路、技巧而忽视思维是教学的一种硬伤.平时教学或备考,要不断反复提示学生“手中有图(画草图),眼中取势(动态趋势),心中明道(数学知识、思想和眼光),脑中优术(解题方法与策略)”,确保“学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程”.教学一定要“明确”,谨记在三个“防范”和三个“追问”中,尤其是在不脱离课程标准要求的情况下,尽可能做好初、高中数学的有效衔接,为学生后续学习和发展奠基.

