煤斗调频减震火电厂结构优化设计及减震性能分析

康迎杰， 彭凌云， 彭奕亮， 薛 涛， 杲晓龙， 苏经宇

(1. 北京工业大学 工程抗震与结构诊治北京市重点实验室，北京 100124； 2. 河南省电力勘测设计院，郑州 450007；3. 国核电力规划设计研究院，北京 100095； 4. 同济大学 土木工程学院，上海 200092)

2016年中国火力发电量占全部总发电量的比例为74.37%，并且在未来很长的一段时间内，火力发电的主导地位不会发生变化，此外在日本、印度、美国、土耳其等许多国家中火力发电亦发挥着非常重要的作用。火力发电厂作为生命线工程，保证其在地震作用下的抗震安全性至关重要，火电厂结构往往采用薄弱环节较多的框排架结构形式[1]，为此将消能减震技术应用在火电厂主厂房结构中显得尤为必要。在超高层、高耸、及大跨结构中，调谐质量阻尼器(Tuned Mass Damper，TMD)作为一种减振控制技术已被广泛应用与研究[2]，为了弥补单一TMD频率敏感、鲁棒性差的缺点，双重调频质量阻尼器和多重调频质量阻尼器(Multiple Tuned Mass Damper，MTMD)被相继提出[3]，随后研究表明MTMD与TMD相比具有更好的减震效果和减震稳定性[4-5]。作为调频减震理论的应用拓展，一些学者在大型火电厂主厂房结构抗震设计中展开了对煤斗减震技术的应用研究，现阶段的煤斗减震设计方法主要包括悬吊式和支承式[6-8]，煤斗调频减震结构与传统附加额外质量到结构上形成TMD的构造不同，在火电厂中以煤斗质量作为TMD的质量单元，形成了火电厂主厂房特有的减震结构形式。在侧煤仓火电厂主厂房结构中，多个煤斗布置在整体结构的中上层，高度可达25～40 m，煤斗总质量较大，与结构总质量之比可达到20%～35%左右，对于传统火电厂结构这往往成为抗震不利因素，会导致结构质量分布不均，煤斗层出现“强梁弱柱”，并形成复杂异型节点等问题[9]。但若采用调频减震理论利用煤斗质量进行振动控制，煤斗则提供了非常可观的质量，并且其布置位置也对调频减震有利。

现阶段被动型调频减震优化方法主要包括基于经典定点理论推导的单自由度系统的TMD和MTMD优化设计方法[10]，针对多自由度系统分别提出的TMD单模态控制和MTMD单模态或多模态控制设计方法[11-12]，采用的优化目标函数主要包括基于简谐激励作用下的结构响应动力放大系数和基于随机激励作用下的结构动力响应均方值[13]。

本文将典型侧煤仓火电厂结构简化为多自由度剪切型模型，基于调频减震理论对单重和多重煤斗调频减震火电厂结构的优化设计方法进行了研究，选取典型侧煤仓火电厂结构进行煤斗减震设计，进行了53组地震动作用下的弹性时程分析，检验煤斗调频减震结构相对传统结构的减震效果。由于结构进入弹塑性阶段后，调频减震效果会发生变化[14]，为此采用弹塑性时程分析方法，对结构发生弹塑性变形后煤斗减震的控制效果加以考察。

1 煤斗减震结构设计理论

传统火电厂结构的煤斗通常固定连接在框架梁上，煤斗减震结构中可采用悬吊或者支承的方式放松煤斗约束，同时设置弹性和阻尼元件进行调频减震设计，如图1(a)所示。图1(b)所示为支承式煤斗减震构造示意图[15]。煤斗和框架梁间可采用支座连接，支座承担了煤斗的重力作用，同时提供水平弹性力及阻尼力，可通过阻尼器来调整减震煤斗的阻尼比，在火电厂结构中多个煤斗往往并排布置，每个煤斗可采用同样布置方式，煤斗的设计参数主要包括弹性刚度ki,i=1,2,…,n及阻尼系数ci,i=1,2,…,n(或阻尼比ξi,i=1,2,…,n)，其中n为煤斗的总数量。

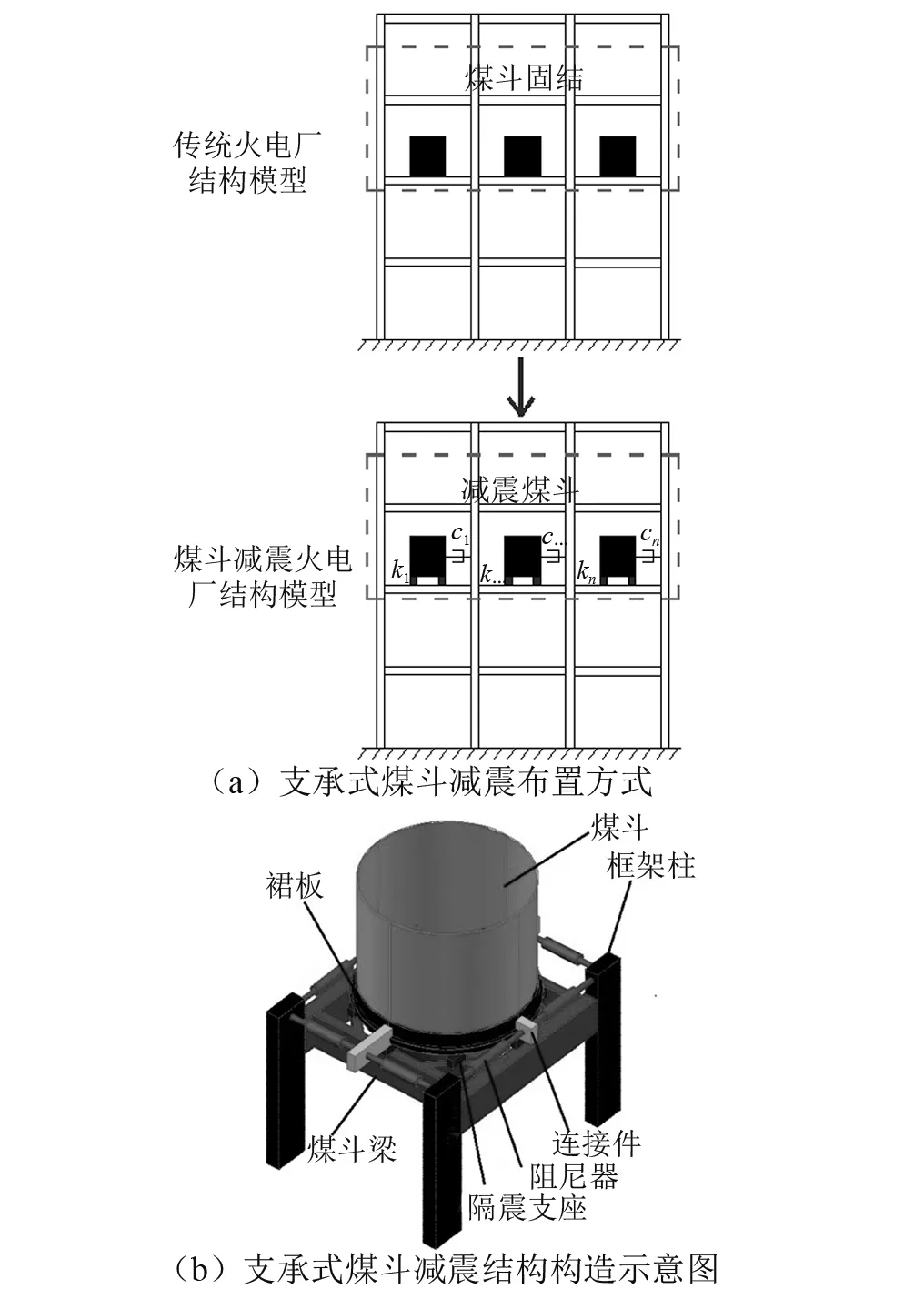
图1 煤斗减震火电厂结构简化模型Fig.1 The simplified model of coal-fired power plant building with coal bucket dampers

1.1 结构动力响应传递函数

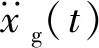
(1)

(2)

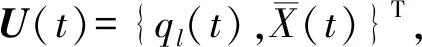
(3)

(4)

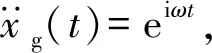
(5)

第l阶振型广义坐标ql的传递函数为y(ω)的第一个元素，通过计算可得

(6)

式中：ηl,ξl,ωl分别为第l阶振型参与系数，振型阻尼比和振型圆频率。

1.2 优化设计目标函数

假定地震激励为平稳随机白噪声过程，S0为地震波功率谱密度，结构主控振型的广义坐标ql响应方差为

(7)

火电厂结构中，各个煤斗质量相差不大(mp=md)， 若将n个煤斗的设计参数统一(ωp=ωd,ξp=ξd)则为TMD减震系统，式(6)得

(8)

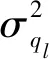
(9)

将n个煤斗的自振频率按照等间隔分布则为MTMD减震系统，假定各个减震煤斗的阻尼比相等(ξp=ξd)， 煤斗频率比覆盖范围为βωl，频率比间隔则为βωl/(n-1)，ωd为n个减震煤斗频率的平均值， 假定ωd=λωl，λ定义为MTMD系统的频率比则有

(10)

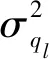
(11)

具体参数寻优流程如图2所示。首先确定无煤斗火电厂结构主控振型的动力特征(ηl,ξl,ωl,φl)及减震煤斗设计方案(TMD或MTMD)，然后分别确认频率比λ、频率比覆盖率β及煤斗阻尼比ξ的寻优范围，其中λ和ξ的寻优范围，可采用由经典公式计算的最优值向两侧扩展，β取值在[0,2)，β=0时即为TMD减震方案，在上述最优参数寻优范围内，根据上述式(6)、式(7)、式(9)和式(11)计算各个参数下目标函数值，随后寻找目标函数最小值，其对应的参数即为最优设计参数，优化寻优过程宜采用MATLAB等编程软件进行计算处理。

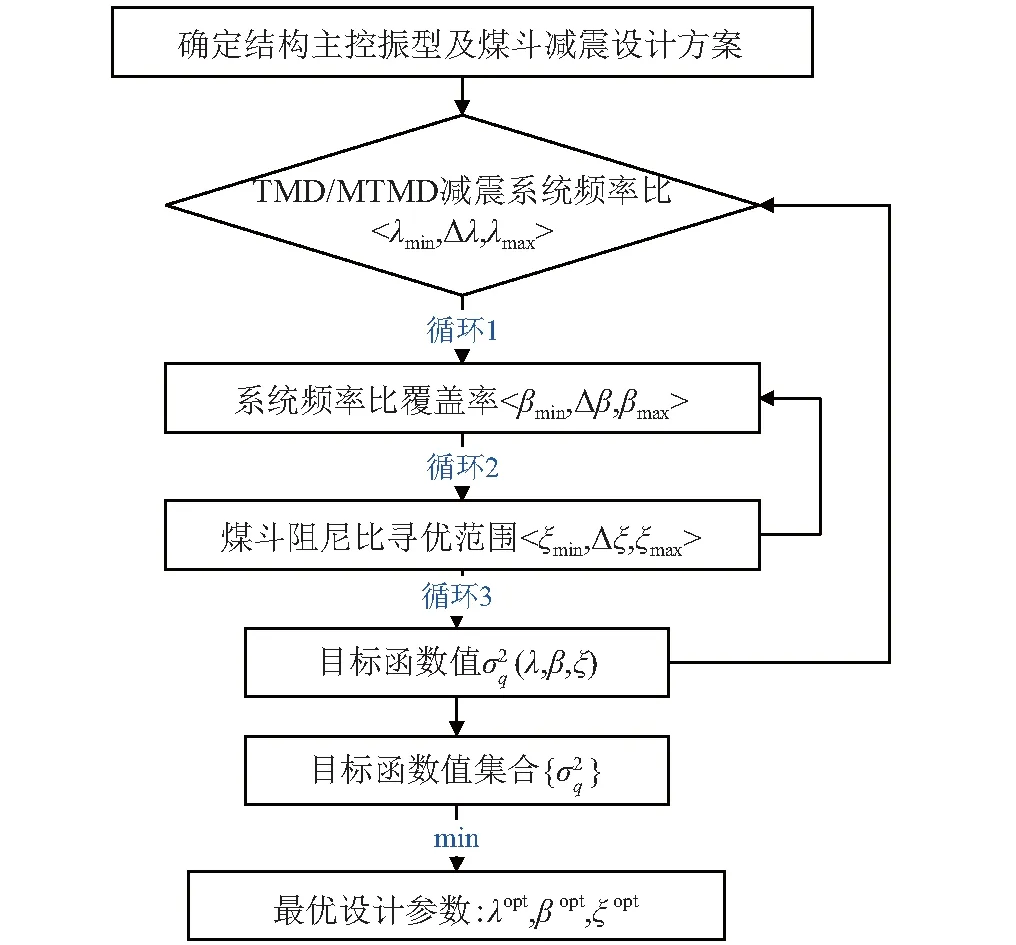
图2 参数寻优流程图Fig.2 Parameter optimization process

2 工程算例

2.1 工程背景

选取某典型侧煤仓火电厂结构模型作为研究对象，如图3所示。工程主体为8层钢筋混凝土框架结构，高62.65 m，横向(y向)3跨20.4 m，纵向(x向)8跨73.6 m，基本地震烈度为7度(0.15g)，场地类别为Ⅲ类，设计地震分组为第二组，场地特征周期Tg=0.55 s，抗震设计等级为一级。结构第4层一共布置了12个煤斗，煤斗具体布置位置如图3(b)所示。每个煤斗质量为580 t，煤斗总质量占去除煤斗后火电厂结构总质量的29.2%，传统煤斗固接布置的结构记为模型1(YJG)，结构主要梁柱构件详细信息如表 1所示。

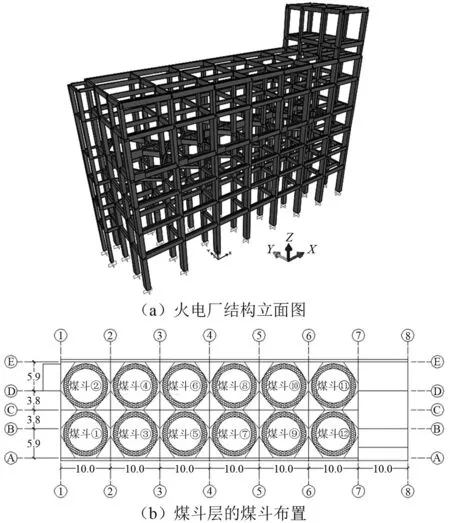
图3 侧煤仓火电厂主厂房结构模型Fig.3 Structural model of side bunker coal-fired power plant

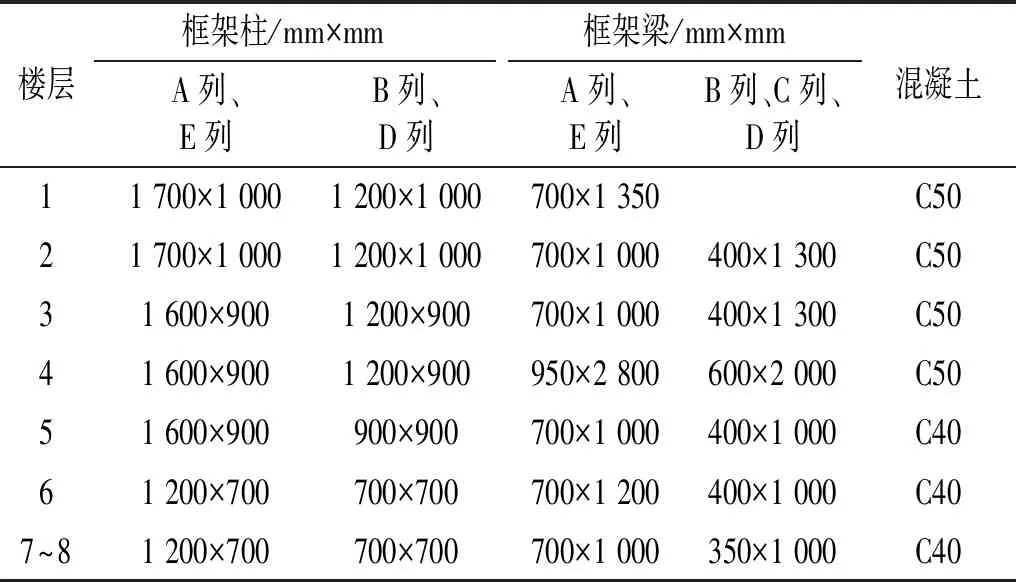
楼层框架柱/mm×mmA列、E列B列、D列框架梁/mm×mmA列、E列B列、C列、D列混凝土11 700×1 0001 200×1 000700×1 350C5021 700×1 0001 200×1 000700×1 000400×1 300C5031 600×9001 200×900700×1 000400×1 300C5041 600×9001 200×900950×2 800600×2 000C5051 600×900900×900700×1 000400×1 000C4061 200×700700×700700×1 200400×1 000C407～81 200×700700×700700×1 000350×1 000C40

2.2 煤斗减震设计参数

侧煤仓火电厂结构平面布置较为规则，去除煤斗质量后的结构记为模型2(YJG′)，第1阶振型为纵向平动振型，振型质量参与系数0.86，选取结构第1振型作为主控振型，第1阶振型的主要动力特性如图4所示。煤斗减震设计参数分别按照上述TMD和MTMD减震系统的优化目标函数确定，其中MTMD减震方案按照煤斗组合方式分为3种方案，具体方案设计如表2所示。

图4 无煤斗火电厂结构模型第1阶振型Fig.4 First mode of coal-fired power plant without coal buckets

方案煤斗组合TMD①～MTMD 12①②③④⑤⑥⑦⑧⑨⑩MTMD6①②③④⑤⑥⑦⑧⑨⑩MTMD3①～④⑤～⑧⑨～

根据目标函数和结构主控振型的动力特性，采用数值算法确定煤斗减震的最优设计参数。如图5(a)～ 图5(d)所示为4种煤斗减震方案在最优频率覆盖范围β=βopt的条件下，目标函数值与λ和ξd的空间变化关系，图6(a)和图6(b)所示分别为在最优频率比或最优阻尼比条件下，目标函数值与ξd或λ的变化关系曲线。从图6可知：

(2) 在最优参数条件下，MTMD减震方案的方差减震效果稍优于TMD减震方案，TMD方案目标函数最小值比MTMD方案约高8.7%，MTMD方案的目标函数值离散程度较小，且随TMD数量的增加而变小。

(3) 在最优频率比条件下，当TMD和MTMD的阻尼比参数小于最优阻尼比参数时，目标函数显著加剧，控制效果很差，而阻尼比参数大于最优阻尼比参数时，目标函数增加程度较为缓和，可以保证减震效果的稳定性，如图6(a)所示。为此在进行煤斗减震设计时，可以适当增大煤斗的阻尼比以保证减震效果的可靠性。

(4) 最优阻尼比条件下，在TMD和MTMD最优频率比附近的一定区间范围内，减震效果较为稳定，其中MTMD的频率比区间要明显优于TMD的频率比区间，MTMD6与MTMD12的区间较为相当，并优于MTMD3方案。

图6 优化目标函数与ξd,λ的变化曲线Fig.6 Variation of objective function value with ξd,λ

2.3 有限元模型及筛选地震波

采用SAP2000 软件建立火电厂煤斗减震结构有限元模型，将每个煤斗的质量平均分为四等份并以节点质量形式模拟，通过LINK单元将节点质量与煤斗梁连接，LINK单元的刚度和阻尼属性按照各煤斗减震方案的最优参数确定，4种减震方案下，各个减震煤斗的质量、弹簧刚度及阻尼参数如表 3所示，其中各煤斗质量一致为580 t，在弹性分析阶段有限元模型的材料采用线弹性本构模型，结构振型阻尼比取为0.05，单个减震煤斗模型及整体结构煤斗减震模型如图7(a)和图7(b)所示。

考虑到调频型减震控制受地震波离散性的影响较大，为提高煤斗减震结构减震效果的可靠性，选取FEMA P695报告[16]建议的22条远场地震波(编号1～22)、28条近场地震波(编号23～50)、2条人工波(编号51～52)和Elcentro地震波(编号53)，共53条地震波作为输入地震波， 53组地震波的绝对加速度反应谱，如图8所示。对结构进行时程分析时，地震波峰值加速度按照55 cm/s2调幅。

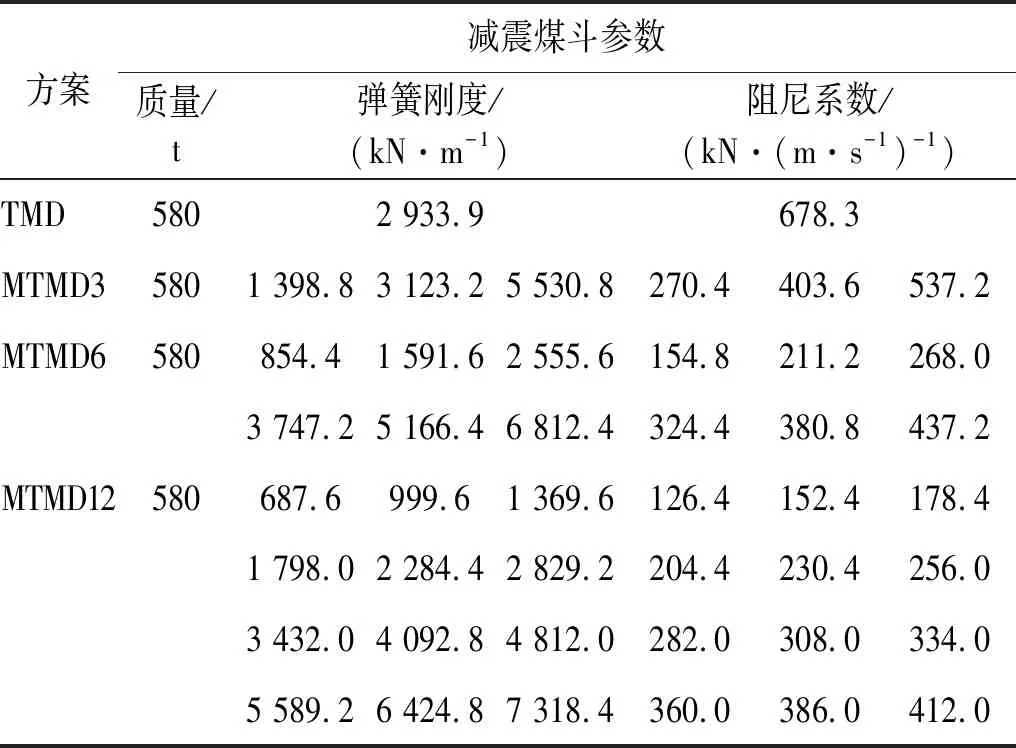
表3 减震煤斗设计参数

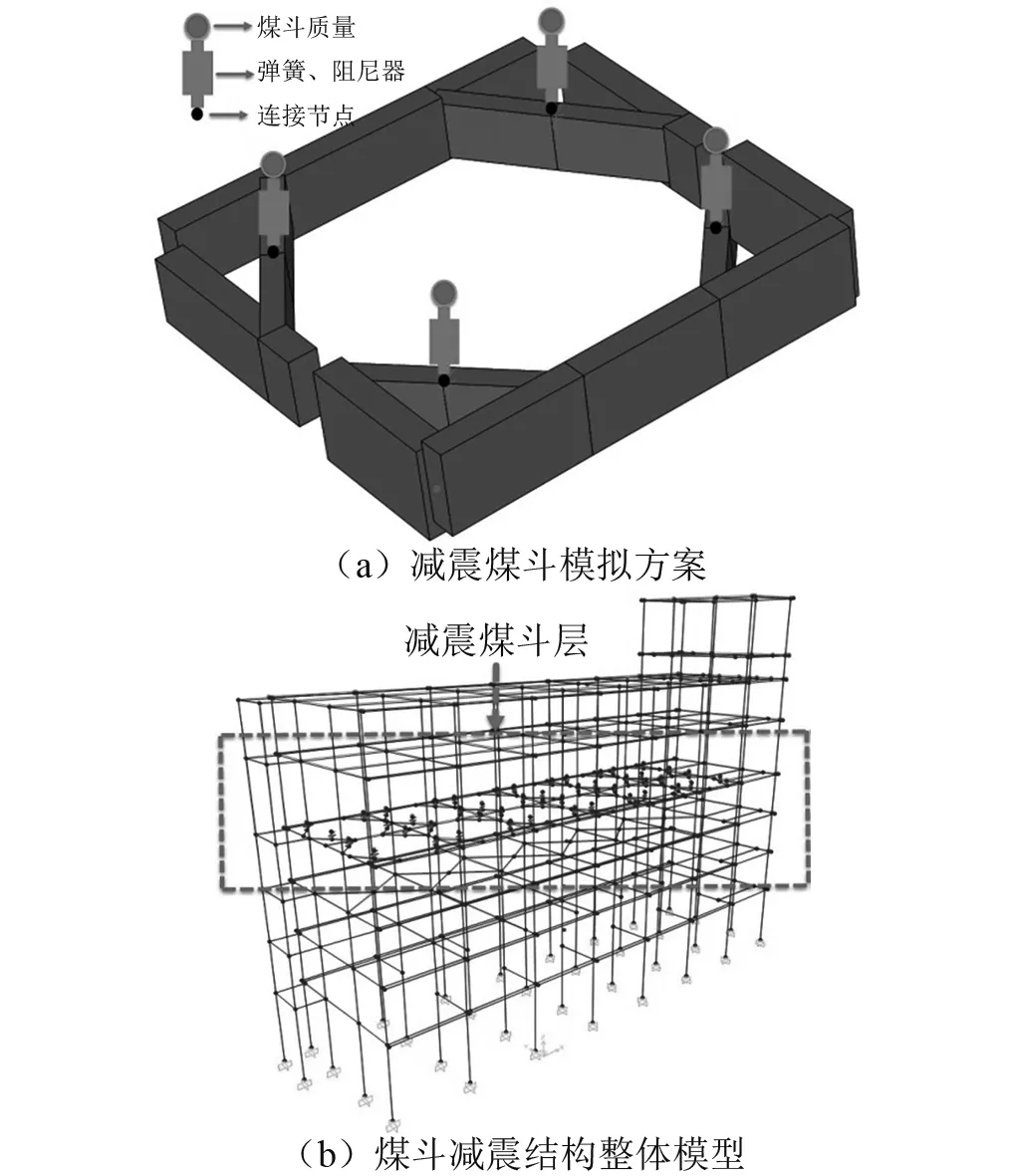
图7 煤斗减震结构数值分析模型Fig.7 Finite element model of the structure with coal bucket dampers

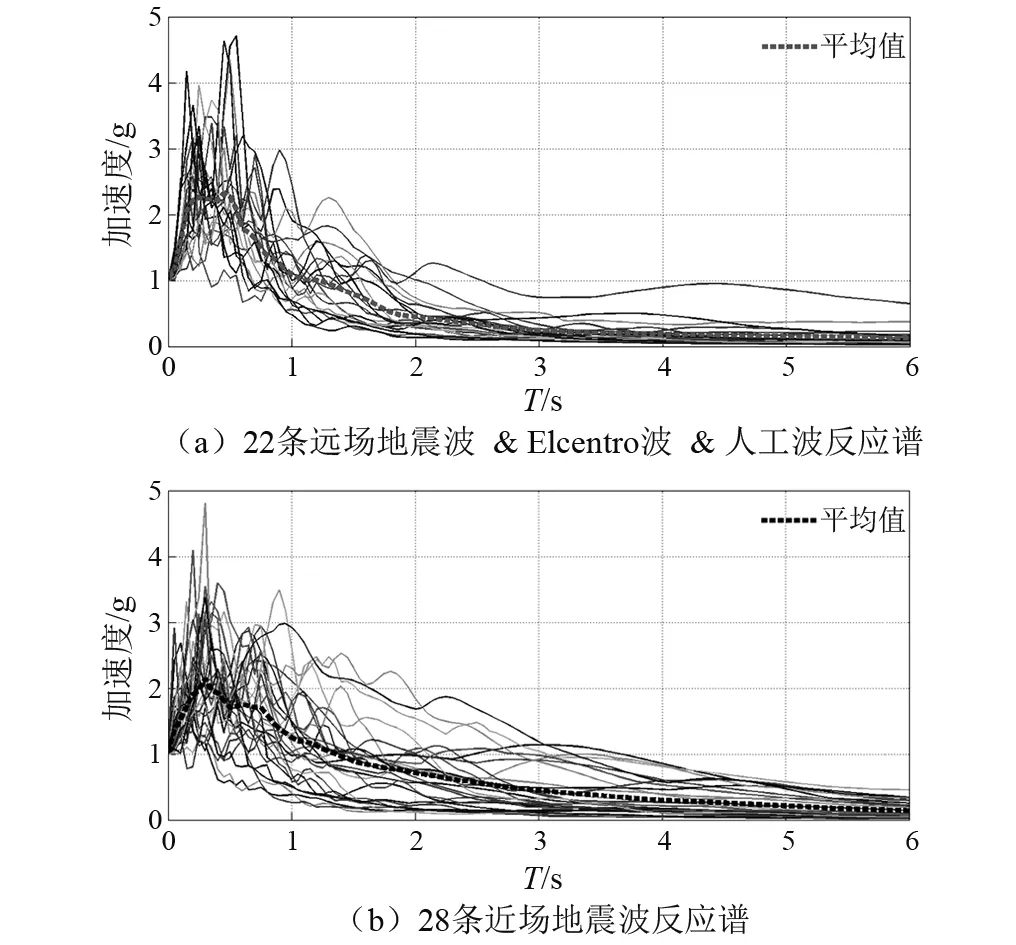
图8 53组地震波反应谱Fig.8 The response spectrum of 53 sets of seismic waves

3 减震效果分析

在53组地震波作用下，采用时程分析法对4种煤斗减震方案的控制效果(相对与传统结构模型1)进行分析，分析结果主要包括：结构层间变形的减震效果、结构顶层位移的减震效果及结构基底剪力的减震效果。采用均方根减震率作为结构减震效果的评价指标，定义结构动力响应均方根(Root Mean Square, RMS)

(12)

式中： 均方根减震率由η=(R-Rd)/R计算；xi为i时刻结构动力响应；N为采集的总点数；R为原结构动力响应均方根；Rd为煤斗减震结构动力响应均方根。

3.1 结构响应减震效果

图9(a)所示为原结构和4种煤斗减震结构在53组地震波作用时各层最大层间位移角平均值分析结果，图9(b)所示为4种减震方案各个楼层层间位移角减震率统计结果，从图9可知：①4种煤斗减震方案对结构的层间变形起到了良好的控制效果，3种MTMD方案的减震效果较为相当，TMD方案的减震效果要稍优于3种MTMD方案；②煤斗减震方案对结构煤斗层及其以下楼层的控制效果(减震率大于40%)明显优于煤斗层以上楼层，对鞭梢效应突出的第7、第8层控制效果较小(减震率在5.9%～10.5%)。

图10(a)所示为4种煤斗减震方案下，结构顶层位移均方根减震率统计结果，图10(b)所示为在Elcentro波作用下，原结构与煤斗减震结构顶层位移时程曲线，从图10可知：①在53组地震波作用下，4种煤斗减震方案的减震趋势较为一致，减震效果良好且平均减震率都到达了45%及以上，其中TMD方案减震效果稍优于3种MTMD减震方案；②与原结构相比，煤斗减震使得结构顶层位移的振动循环过程增多，在结构位移增大时，减震煤斗对结构施加与结构运动反向的作用力，从而抑制结构位移的进一步增大，达到结构振动控制的效果；③不同地震波的减震效果表现出一定的离散性。

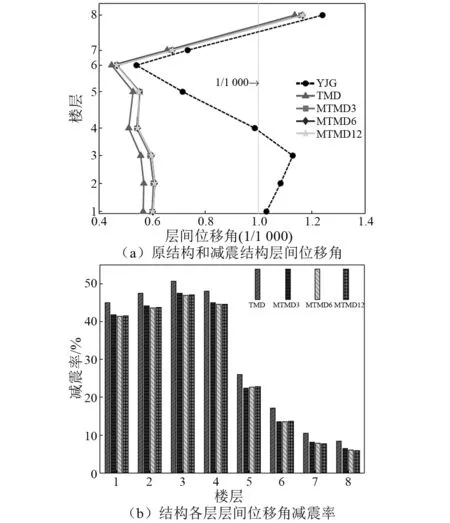
图9 煤斗减震结构层间位移角减震效果Fig.9 Damping effect of structural story drift

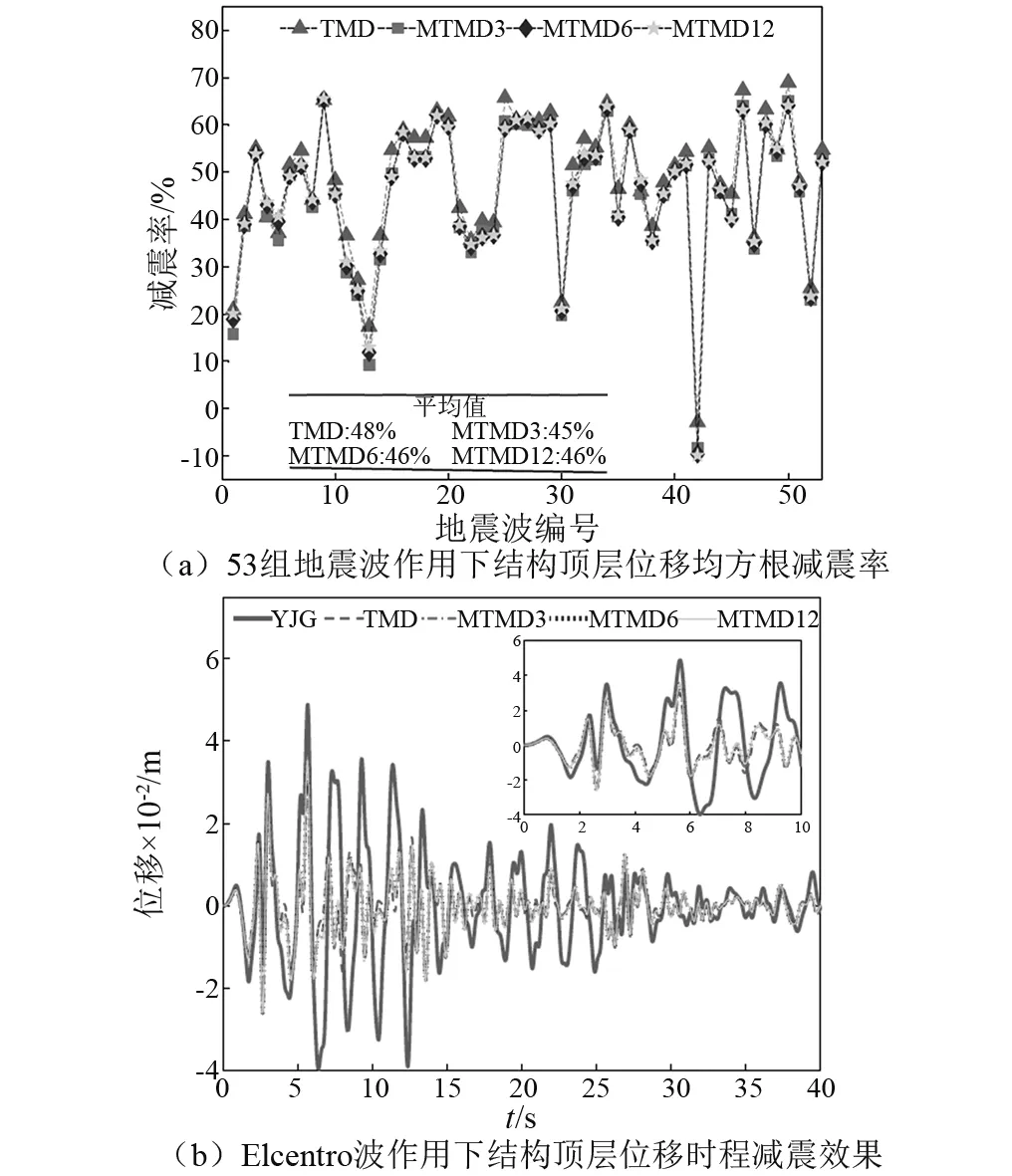
图10 煤斗减震结构顶层位移减震效果Fig.10 Damping effect of structural roof displacement

图11 (a)所示为结构底部剪力均方根减震率统计结果，图11(b)所示为在Elcentro波作用下，原结构与煤斗减震结构底部剪力响应时程曲线，从中可以看出结构底部剪力减震率与顶层位移减震率的变化趋势一致，随地震波的不同表现出一定的离散性，但4种煤斗减震方案对应的结构底部剪力减震率平均值都超过51%，减震效果非常可观。

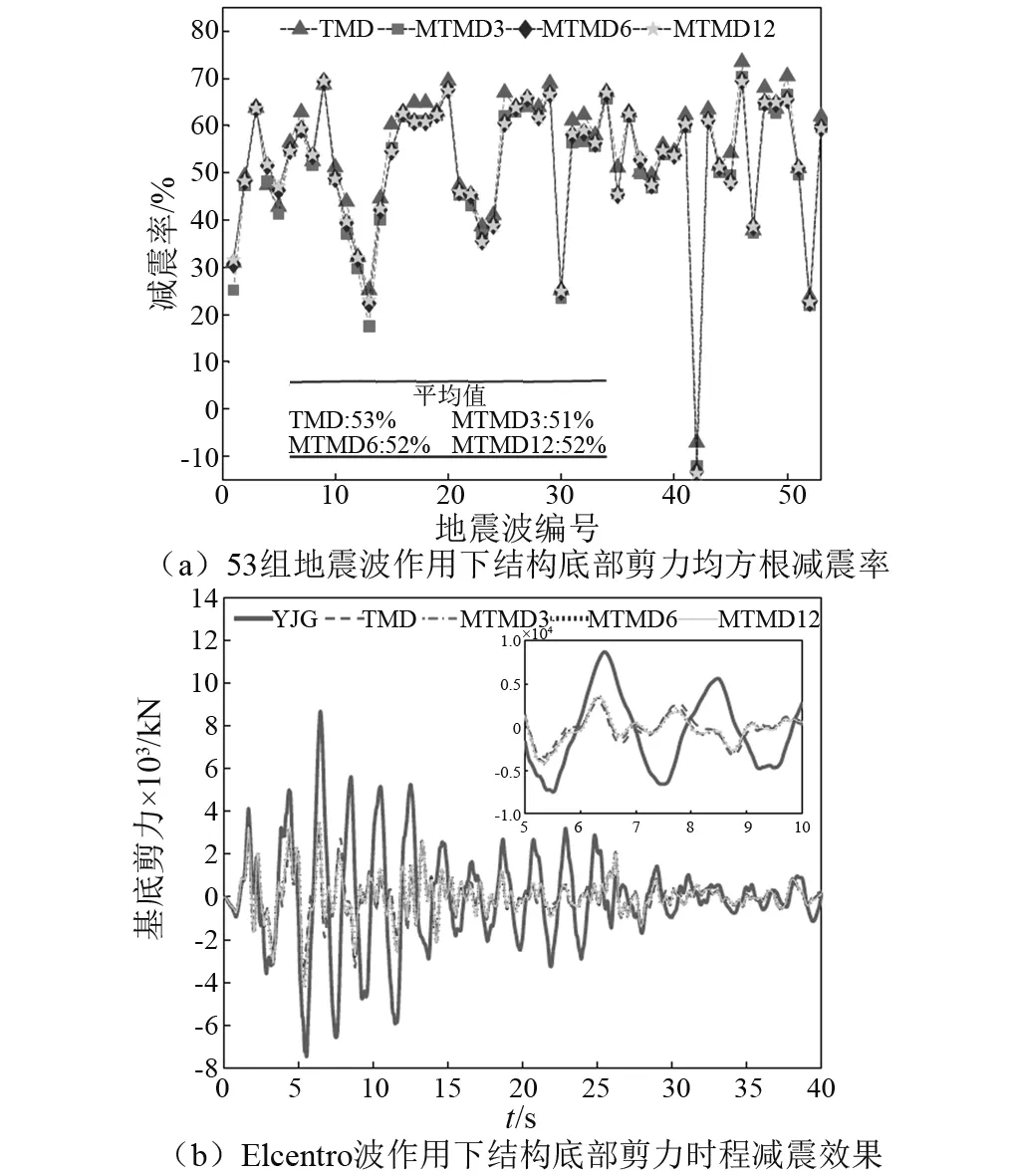
图11 煤斗减震结构底部剪力减震效果Fig.11 Damping effect of structural base shear force

3.2 减震率离散性分析

首先对煤斗调频减震机理进行分析，如图12所示为原结构和煤斗减震结构第1阶振型模态位移传递函数幅值，其中针对TMD减震方案，激励频率在2.55～5.35 Hz时，煤斗减震表现出良好的减震效果，此区间即是有效减震区域，当激励频率小于2.55 Hz时，煤斗减震则对结构位移产生放大效应，当激励频率大于5.35 Hz时，减震前后的结构位移响应较为相当，以此表明调频减震的控制效果受激励频率的影响甚大。从结构位移响应方面来看，当激励频率与结构自振频率接近时，结构发生共振响应剧烈，但此时调频减震控制效果显著，抑制结构的强烈震动；当激励频率远离结构自振频率时，调频减震对结构位移响应产生一定的放大效果，但此时结构响应本身较弱，结构并未发生明显的强烈震动。在结构受到外界荷载作用时，其中与结构自振频率临近的荷载分量往往会对结构产生较大的振动作用，此时调频减震可以发挥较好的减震效果，因此调频减震在控制结构地震响应方面是有效的，另外可以看出MTMD与TMD具有相似的作用效果。

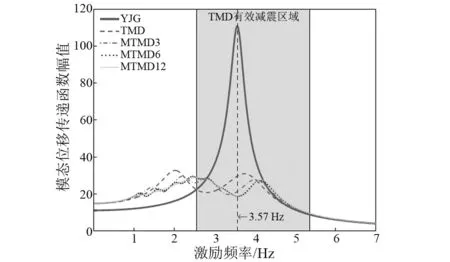
图12 结构模态位移传递函数幅值Fig.12 Transfer function amplitude of structural mode displacement

经对53组地震波的减震效果分析可知，煤斗减震对结构的动力响应整体表现出较好的控制效果，但在不同地震波作用下，减震率有一定的离散性。由上述对调频减震机理分析可知，调频减震的控制效果受激励频率的影响甚大，而各个地震波频谱的差异性较大，这就导致不同地震波作用时，煤斗减震效果出现离散性，个别工况出现了负控制现象。为检验煤斗减震结构具有足够的抗震安全性，选取第42条地震波和Elcentro波作为分析工况，其中在第42条地震波作用下，减震结构的动力响应比原结构的动力响应有所增大，4种煤斗减震方案的顶层位移均方根放大率在2.9%～9.9%；在Elcentro波作用下，4种煤斗减震方案顶层位移减震率在52.1%～54.7%。首先对两条地震波的频谱特性、反应谱特性和结构层间位移角进行对比分析如图 13所示。从图13可知：①从两条波的频谱对比来看，在结构主控振型频率附近，第42条地震波的频率分量明显小于Elcentro波，同时根据上述调频减震机理，在有效减震区域内Elcentro波的频率分量较大，煤斗减震对其控制效果良好；在非有效减震区域内，第42条地震波的频率分量较大，煤斗减震并未有减震控制效果，导致煤斗减震出现负控制现象；②从两条波的反应谱对比来看，第42条地震波在结构主控振型周期附近的反应谱为Elcentro波对应反应谱的1/5，造成结构在Elcentro波作用时动力响应明显强于第42条地震波，此即意味着Elcentro波对原结构的动力作用比第42条地震波的动力作用明显较大，导致原结构在Elcentro波作用下的层间位移角明显大于第42条地震波的层间位移角结果，如图13(c)结果所示；③地震波在有效减震区域内的频率分量越多，结构响应越大，煤斗调频减震控制效果越好，地震波在非有效减震区域内的频率分量越多，煤斗调频减震控制效果较差，甚至出现负控制效果，但结构响应本身较小，结构不会出现强烈的动力响应，从图13(c)可知，TMD减震结构在第42条地震波作用下，层间位移角出现局部放大，但其仍明显小于Elcentro波作用下的位移角。

由上分析，调频减震的控制效果对激励频率非常敏感，各个地震波的频率组成具有显著差异性，因此煤斗减震结构的减震效果必将表现出一定离散性，其中对结构响应较大的地震波工况减震效果显著，而在减震效果较差的地震波工况中，结构本身的动力响应较小，其抗震安全裕度较大，并未对结构产生明显负面效应，所以煤斗减震对提高结构的抗震性能具有良好的适用性。

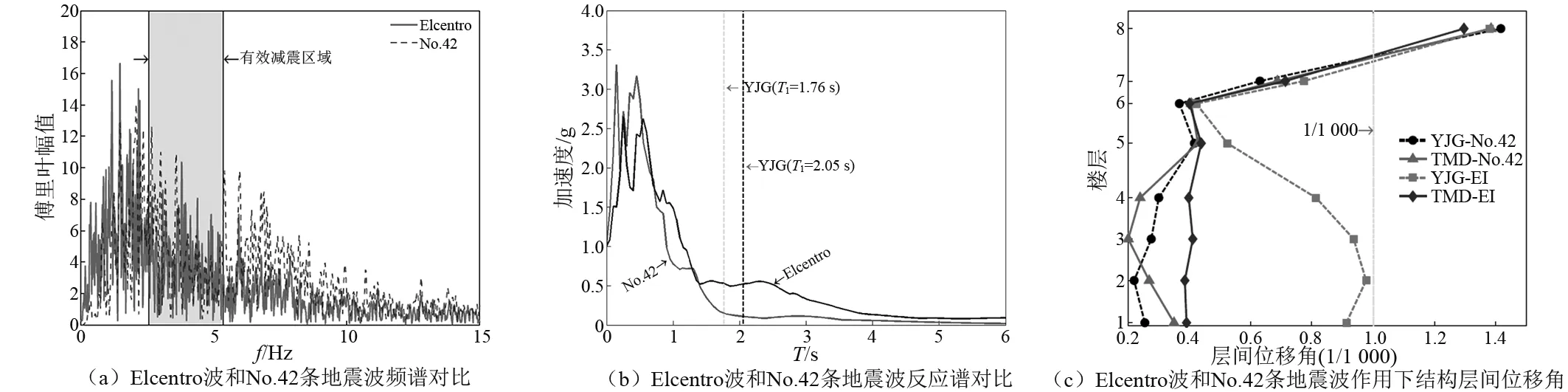
图13 不同地震波作用下煤斗减震结构减震差异性Fig.13 Different damping effect of different seismic waves

4 弹塑性阶段减震分析

为检验结构在进入弹塑性阶段后煤斗减震的控制效果，本文采用ABAQUS有限元软件对侧煤仓原结构和煤斗减震结构进行弹塑性时程分析，采用一维杆件纤维束单元B31模拟结构框架梁、框架柱，该单元能够同时考虑弯距和轴力的耦合效应[17]，采用刚性隔板假定模拟楼板的作用效用，结构材料采用了ABAQUS提供的UMAT接口编制的钢筋、混凝土用户子程序，其中钢筋采用了Clough本构模型考虑Bauschinger 效应引起的刚度退化，混凝土材料本构与OpenSees[18]中的Concrete02本构模型一致。结构阻尼取0.05，采用瑞雷阻尼实现，地震波选取Elcentro波，为使结构进入较强的弹塑性阶段，地震波峰值取为510 cm/s2。

侧煤仓火电厂结构第7、第8层“鞭梢效应”较为突出，地震作用时结构响应较大，可通过特殊方案对其进行局部加强，以结构第1～第6层的地震响应作为评价整体结构抗震性能的标准。原结构第3层为结构薄弱层，最大层间位移角为1/95，4种煤斗减震结构的控制效果基本一致，且最大层间位移角同样出现在第3层为1/142，减震率达到33.1%，如图14所示。结构顶层位移时程曲线表明4种减震结构的位移响应结果较为一致，与原结构相比位移响应明显减弱，其均方根减震率达到约37%，如图15所示。

根据数值分析结果中纤维单元的压、拉应变的大小将结构构件的损伤程度分为轻微损伤、中度损伤、较严重损伤和严重破坏4种状态，侧煤仓火电厂原结构在弹塑性阶段的第D列构件损伤结果如图16(a)所示，原结构在第1～第3层框架梁两端基本全部出现了塑性铰，第3～第5层框架柱出现了较多的塑性铰，其中第3层梁铰已达到较严重损伤程度，第4层的框架柱柱顶达到中度损伤程度。图16(a)所示为MTMD6减震结构第D列构件塑性铰分布结果，通过对比可以看出结构第1、第2层梁铰基本消失，第3层梁铰的损伤状态由较严重损伤下降到轻微损伤，第3、第5层的框架柱损伤基本消失，减震结构的塑性铰主要为第3层梁铰和第4层柱铰，且其主要损伤状态仅为轻微损伤，其它3种减震模型的塑性铰分布结果亦有同样的响应结果。

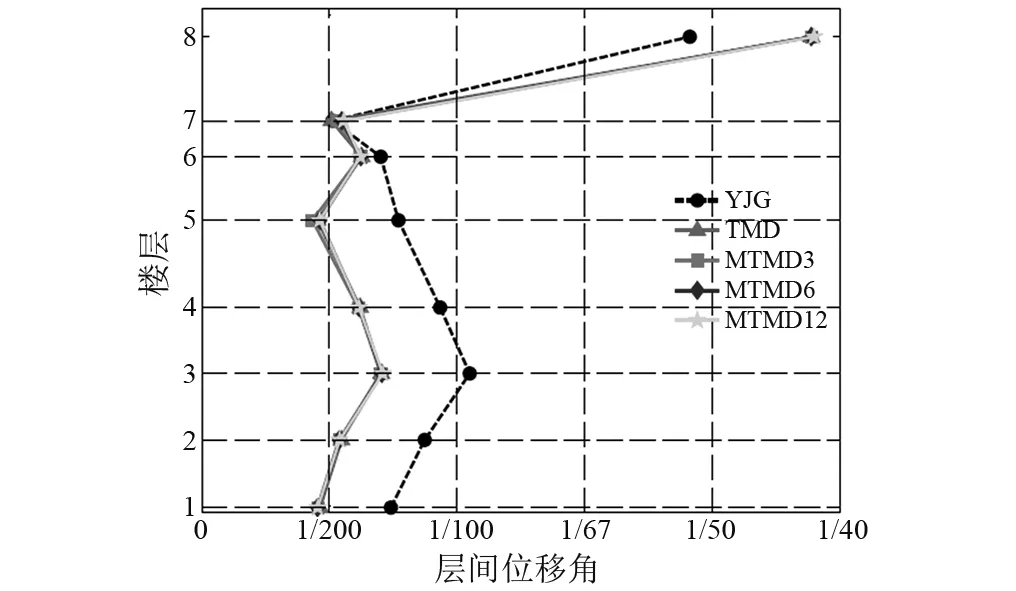
图14 弹塑性阶段层间位移角减震效果Fig.14 Damping effect of structural story drift in the elastoplastic stage

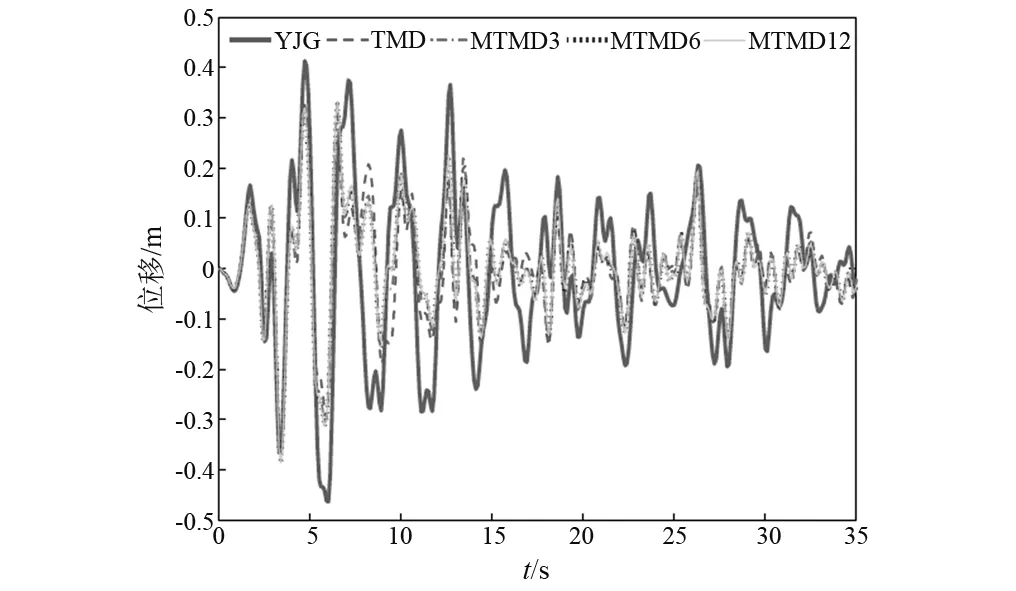
图15 弹塑性阶段顶层位移时程减震效果Fig.15 Damping effect of structural roof displacement in the elastoplastic stage

图16(c)所示为构件损伤统计结果，表明煤斗减震结构构件损伤程度明显降低，各种损伤程度的塑性铰数量都明显下降，其中3种MTMD减震结构的下降率较为一致，而TMD减震结构要稍优于MTMD减震结构。

图16 结构构件损伤减震效果Fig.16 Damping effect of structural member damage

5 结 论

由于火电厂主厂房特殊的工艺要求对结构工程抗震造成了不利影响，为保证结构的抗震安全性，提出了煤斗调频减震结构，即是将其抗震劣势转换为抗震优势，本文通过调频减震理论确定了煤斗减震火电厂结构参数优化设计方法，并采用时程分析法研究了煤斗减震结构的减震效果和结构进入弹塑性阶段后的减震稳定性，主要得出以下几点结论：

(1) 按照调频减震理论获得的单重和多重煤斗减震火电厂结构的最优设计参数中，单重煤斗减震结构的最优频率比稍微小于多重煤斗减震结构，而阻尼比明显偏大，最优条件下两种减震结构控制效果相近。

(2) 在结构保持弹性状态条件下，整体来讲，经过优化设计的单重和多重煤斗减震结构的位移响应明显小于原结构，结构层间变形变小，煤斗调频减震振动控制效果良好。

(3) 煤斗减震结构的控制效果具有显著的频率敏感性，因此在不同地震波作用下的控制效果表现出一定的离散性，但能够保证结构具有良好的抗震安全性，并且进入弹塑性阶段后，煤斗减震结构相对传统结构仍具有明显的减震效果。

煤斗减震结构展现了良好的抗震性能和稳定的减震效果，在结构主体进入明显弹塑性阶段时，最优设计参数发生变化，煤斗减震结构的减震稳定性待进一步研究。