基于蚁狮优化算法与迹稀疏正则化的结构损伤识别

陈承滨， 余 岭,2， 潘楚东， 陈泽鹏

(1. 暨南大学 力学与建筑工程学院，广州 510632；2. 暨南大学 重大工程灾害与控制教育部重点实验室，广州 510632)

结构损伤识别(Structural Damage Detection，SDD)是实施结构健康监测[1-2](Structural Health Monitoring，SHM)的关键一步。近年来，采用群智能优化算法将SDD问题转化为数学上的约束优化问题是SDD的一个热门方向。从计算和优化的角度，将结构损伤识别问题看作优化问题，通过定义一个关于系统模型的目标函数，利用优化的手段实现对损伤参数的识别。随着计算机和优化思想的发展，涌现出大量群智能识别方法，如基于粒子群、蚁群、猴群、人工鱼群和人工蜂群等方法，并已取得较好的研究成果[3-7]。但是，大多算法都存在识别精度不足和噪声鲁棒性有待提高的问题。

Mirjalili[8]提出蚁狮优化(Ant Lion Optimizer，ALO)算法，这是一种新型元启发式群智能算法。由于引入了随机游走、轮盘赌策略及精英策略，使得ALO算法成为一种种群多样、寻优性能强、调节参数少、易于实现的搜索技术。近年来，ALO算法已成功应用于杆系结构优化设计[9]、电力系统最优潮流计算[10]及结构高效建模[11]等领域，表现出良好的寻优能力和抗噪鲁棒性，但目前尚未应用于结构损伤识别问题。

本文基于结构损伤前后模态参数建立SDD问题的目标函数，同时引入迹范数约束条件[12]作为稀疏约束项，利用蚁狮优化算法对该目标函数求解以获得结构局部损伤。本文介绍ALO算法基本原理、引入策略及实现流程；给出结构损伤识别优化问题的目标函数并建立简支梁数值模型，并讨论目标函数引入稀疏约束项的必要性；对简支梁的局部损伤进行识别，同时添加人工噪声，研究其对识别精度的影响；最后，利用实测的钢管简支梁实验数据验证ALO算法应用于结构损伤识别的可行性与有效性。

1 蚁狮优化(ALO)算法

1.1 ALO算法基本原理

ALO算法核心思想是模拟蚁狮捕猎蚂蚁的狩猎机制以实现全局寻优。蚁狮在捕猎前会在在沙质土中利用其巨大的下颚挖出一个漏斗状的陷阱，并藏在陷阱底部等待猎物到来。一旦随机游走的蚂蚁落入陷阱时，蚁狮迅速将其捕食，随后重新修缮陷阱等待下一次捕猎。

ALO算法通过数值模拟实现蚂蚁和蚁狮之间的相互作用将问题优化：引入蚂蚁的随机游走实现全局搜索，通过轮盘赌策略和精英策略保证种群的多样性和算法的寻优性能。蚁狮相当于优化问题的解，通过猎捕高适应度的蚂蚁实现对近似最优解的更新和保存。

1.2 蚂蚁的随机游走

蚂蚁在自然界中随机游走寻找食物的过程可以看作各搜索代理搜寻可行域的过程。随机游走的过程在数学上可以表示为

X(t)=[0,cumsum(2r(t1)-1),…,
cumsum(2r(tn)-1)]

(1)

式中：X(t)为蚂蚁随机游走的步数集；cumsum为计算累加和；t为随机游走的步数(本文取最大迭代次数)；r(t)为一个随机函数，定义为

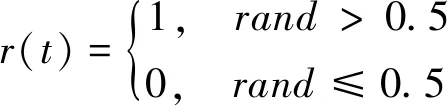
(2)

式中：rand为[0,1]的随机数。

由于可行域存在边界，不能直接用式(1)更新蚂蚁的位置。为确保蚂蚁在可行域范围内随机游走，需根据式(3)对其进行归一化

(3)

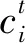
1.3 蚁狮对蚂蚁随机游走的影响

蚁狮制造的陷阱会影响蚂蚁随机游走的路线，为对此假设进行数学建模，提出

(4)

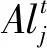
1.4 自适应机制

通过轮盘赌策略选择某只蚂蚁具体被哪只蚁狮捕食，每只蚂蚁只能被一只蚁狮捕食，而适应度越高的蚁狮捕获蚂蚁的概率越大。另外，蚂蚁一旦落入蚁狮制造的陷阱，蚁狮就会向陷阱边缘抛沙以防止蚂蚁逃脱。此时，蚂蚁随机游走的范围将急剧缩小。通过下列方程模拟这种现象

(5)

(6)

式中：I为比例系数；T为最大迭代次数；v为一个随着迭代次数增大而变化的数(本文取0.1T0.95T时v为6)。

当蚂蚁的适应度值比蚁狮小时，则认为蚁狮将其捕获，此时蚁狮会根据蚂蚁的位置来更新位置

(7)

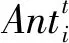
1.5 精英策略

每次迭代后，选择适应度最好的蚁狮作为精英蚁狮。第t只蚂蚁在第t+1次迭代的位置由式(8)确定

(8)

1.6 实现步骤

步骤1数据初始化。确定蚂蚁和蚁狮的数量以及变量维数，在可行域内随机初始化它们的位置，并计算相应的适应度值。

步骤2确定精英蚁狮。选择初始化后蚁狮种群中适应度最好的作为精英蚁狮，本文适应度值越小越好。

步骤4每次迭代后重新计算蚂蚁和蚁狮适应度值，根据蚂蚁的位置和适应度更新蚁狮位置，适应度最好的位置为新精英蚁狮的位置。

步骤5判断是否到达最大迭代次数，若到达则输出结果并结束迭代，否则重复步骤3。

2 迹稀疏正则化在结构损伤识别中的应用

2.1 不考虑稀疏约束

本文采用单元刚度折减模拟结构的真实损伤，忽略质量变化产生的影响，则结构的整体刚度矩阵可以表示为

(9)

式中：α为结构损伤因子向量；αi即为第i个单元的损伤程度，将结构损伤因子约束在[0,0.99]， 其中αi=0为单元健康，αi=0.99为单元完全失效；Ki为整体坐标下第i个单元的刚度矩阵；K(α)即损伤量为α时的刚度矩阵。

模型修正结构损伤识别方法的核心思想是寻找合适的计算模型，使计算获得的结构特征参数与实测结构特征参数相一致。本文选取结构固有频率与结构振型作为特征参考值，并给出描述特征相近程度的定量函数为

(10)

(11)

(12)

利用频率与振型，可将结构损伤识别问题转化为数学中优化问题的形式，其目标函数为

(13)

式中：Δ1和Δ2为加权系数。在测量信息完备，忽略噪声影响的理想情况下，利用式(13)进行结构损伤识别可得到最接近真实损伤的结果。但是，在实际工程中不存在理想条件。因此，在实际应用中通常存在两个问题：

(1)实测模态信息有限而待识别参数过多，往往使损伤识别方程出现较大误差，从而导致识别结果产生偏离，即测量数据不完备导致多识别结果[13]。例如，只利用频率去识别简支梁损伤的结果容易出现对称单元误判，这是由于对称单元具有一致的损伤灵敏度。

(2)测量时存在噪声导致识别精度降低，结构损伤识别属于结构动力学逆问题的研究范畴，由结构特征建立的优化问题通常呈现病态性，即微小的信号扰动会给识别结果带来较大的误差[14]。

2.2 考虑迹稀疏约束的目标函数

真实损伤通常只发生在结构的局部位置，在物理空间上具有稀疏性。因此，为提高结构损伤识别的精度，本文在式(13)的基础上，引入迹稀疏约束条件，将目标函数改写为

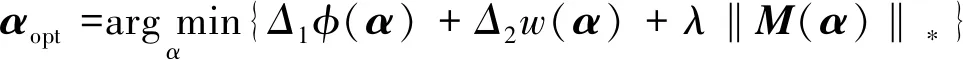
(14)

式中：λ为正则化参数，其数值表示参与程度大小； ‖M(α)‖*为迹范数，表示计算矩阵M的奇异值之和，其中矩阵M(α)=Xdiag(α)，X为设计矩阵。

本文将矩阵X设为

X=A·rand(Nele)

(15)

(16)

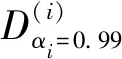
式(14)为迹稀疏约束条件下结构损伤识别方程，可用本文所提ALO算法进行求解。与式(13)比较，其最大的优势在于引入损伤变量的稀疏性约束，既有利于描述真实损伤在物理空间上的稀疏性，又利于改善原来问题的病态程度及提高识别结果的抗噪鲁棒性。

2.3 加权系数的选取

上述定义的目标函数中，采用两个加权系数Δ1和Δ2平衡来自频率与振型的信息。 实际上，频率和振型属于同一结构中两种不同类型的动力指纹。由频率和振型分别构成函数w(α)和φ(α)，在数值上可能出现较大的差异。

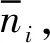
(17)

(18)

(19)

式中：αi取0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，0.99分别进行损伤识别；w(αi)j和φ(αi)j为第j个单元在损伤因子为αi时w(α)和φ(α)的数值； 计算得到Δ1和Δ2分别为0.025和0.975。

3 数值模拟

简支梁有限元模型见图1，梁全长为3 m，共划分为10个单元，所用单元为2结点4自由度单元。其中圆圈内数字为单元编号，其余为节点编号。结构弹性模量Ec=210 GPa； 横截面面积Sc=1.164×10-3m2； 截面惯性矩Ic=7.617×10-7m4； 材料密度Dc=8 590 kg/m3。损伤工况设置见表1，分别考虑单损伤、两损伤及多损伤工况。结构损伤识别时，取结构前5阶固有频率与模态振型，其中振型只提取各单元节点的竖向自由度。同时考察噪声对模态参量的影响，即同时对频率和振型加噪声，噪声添加公式为

rn=rcal(1+LnRn)

(20)

式中：rn和rcal分别为含噪声与不含噪声模态参量；Ln为噪声水平；Rn为以随机矩阵， 表示矩阵Rn内每个数都是[0,1]的随机数。

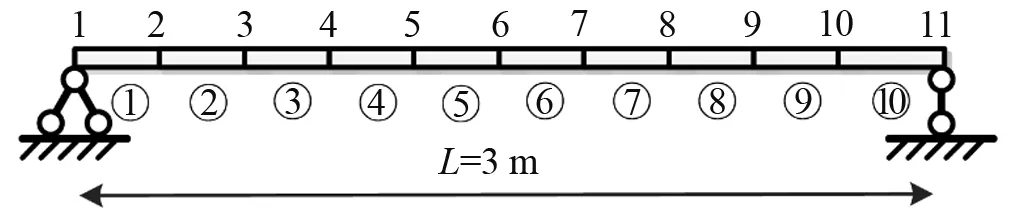
图1 数值模拟简支梁有限元模型Fig.1 Finite element model of simply-supported beam

数值模拟过程在MATLAB2016b版本环境下实现，ALO算法参数设置为：蚁狮数量ALnum=100， 蚂蚁数量Antnum=100， 变量维度dim=10， 最大迭代次数Gmax=100， 蚂蚁随机游走步长n=100， 损伤因子约束在αi∈[0,0.99]，并随机初始化种群位置。针对最小值问题，每个工况计算10次，取10次结果作为最终识别结果。

图2为ALO算法计算本文目标函数的迭代收敛曲线图。由于迭代次数在[80,100]收敛，故取最大迭代次数为Gmax=100次。

另外，本文对是否添加稀疏约束的问题进行了数值模拟，结果如表2所示。从表2可知，考虑稀疏约束的识别结果比不考虑稀疏约束识别结果更趋于真实值，噪声水平越大稀疏约束起到的作用越明显。因此，后续研究都采用添加稀疏约束方案。

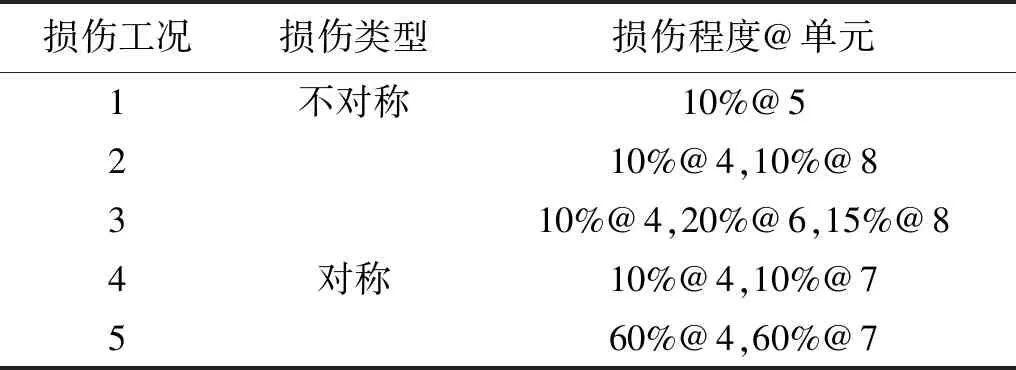
表1 损伤工况及识别结果

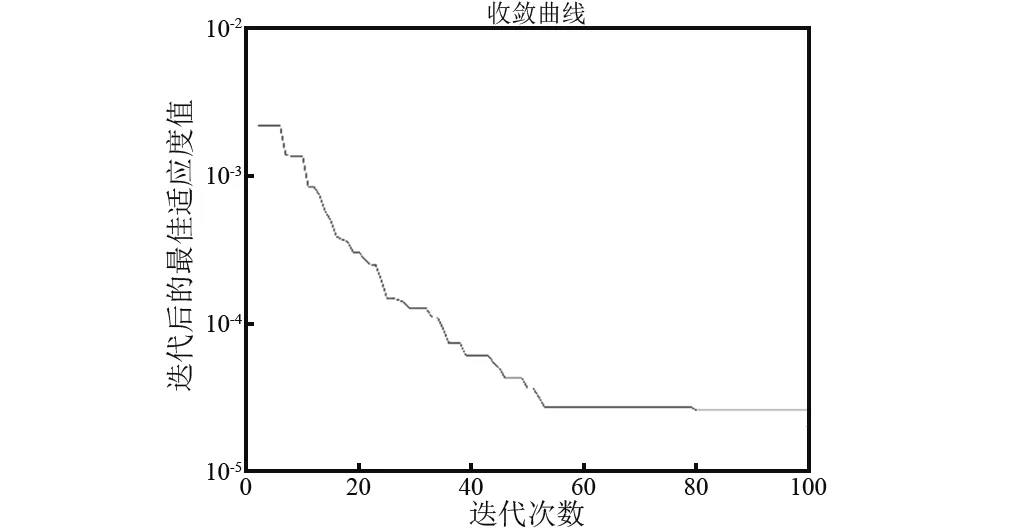
图2 ALO算法迭代收敛图Fig.2 Iterative convergence curve of ALO algorithm

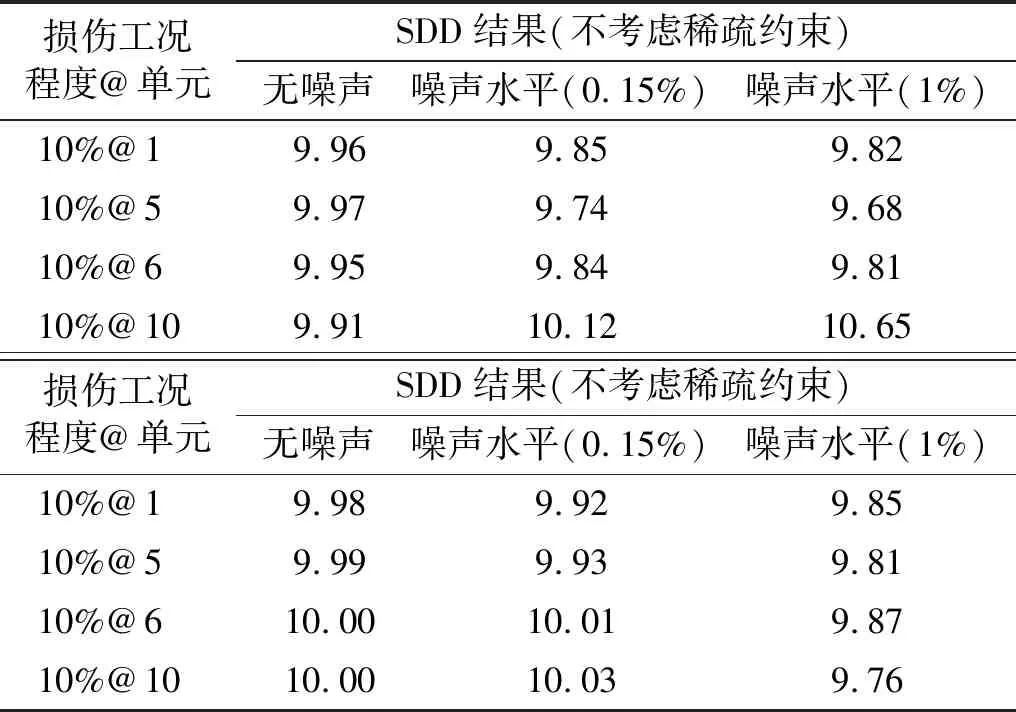
Tab.2 Effect of trace sparse constraint on SDD %

图3～图7为不同噪声水平[15]下各工况损伤单元识别结果。可以看出ALO算法既能准确识别出损伤单元所处位置且能够较为精确的识别出单元损伤程度；工况1出现的误判最少，说明单损伤识别结果好于两损伤及多损伤识别结果；工况4和工况5为对称单元损伤，且对称单元损伤识别结果有互补的趋势，验证了简支梁对称单元具有一致的损伤灵敏度结论。

在图3～图7中，0.15%噪声水平和1%噪声水平下各工况损伤识别结果表明噪声的加入虽会使一些未损伤单元处出现误判，但大部分误判结果均较小，仍可看作无损单元。虽然在高损伤工况5情况下，有个别误判超过5%，但是并不影响ALO算法对损伤单元真实位置及损伤真实程度的判断。结果表明噪声对结构损伤识别结果影响不大，即ALO算法在结构损伤识别过程中具有一定噪声鲁棒性。

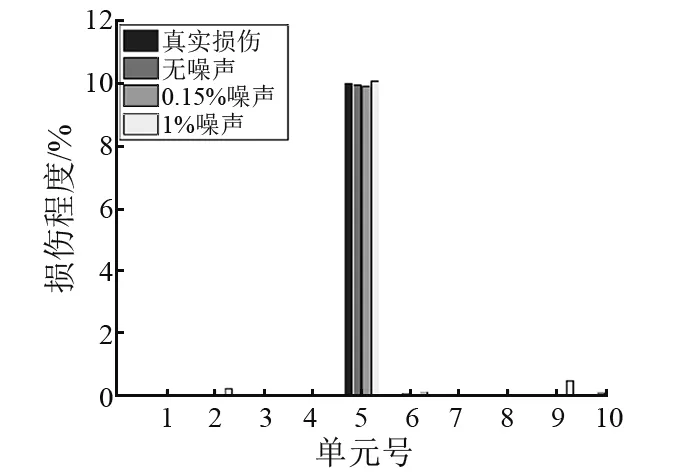
图3 不同噪声水平工况1损伤识别结果Fig.3 SDD results in case 1

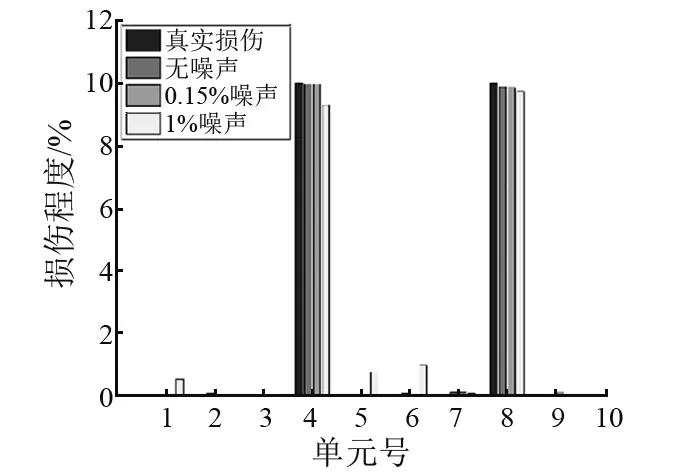
图4 不同噪声水平工况2损伤识别结果Fig.4 SDD results in case 2

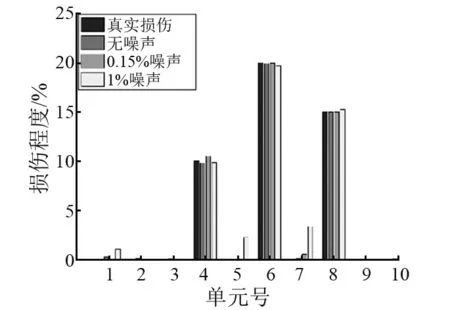
图5 不同噪声水平下工况3损伤识别结果Fig.5 SDD results in case 3

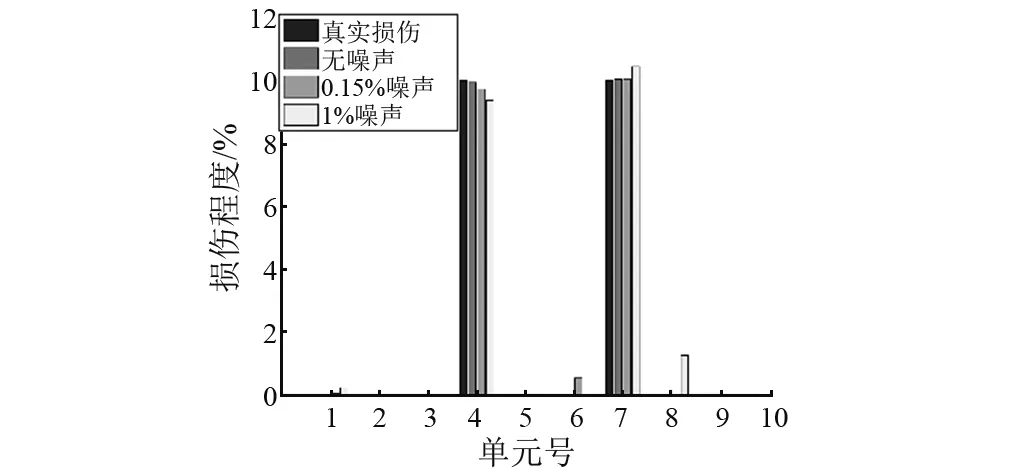
图6 不同噪声水平工况4损伤识别结果Fig.6 SDD results in case 4

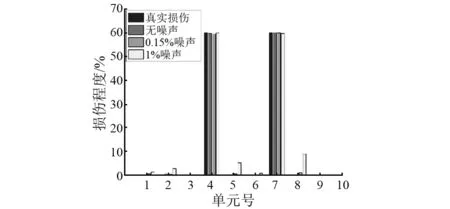
图7 不同噪声水平工况5损伤识别结果Fig.7 SDD results in case 5

4 实验验证

本文实验数据、图8、图9均引自文献[16]。实验模型为3 m长封闭钢管简支梁，外围宽140 mm，高60 mm，钢板厚度3 mm，主梁两端底面横桥向焊接钢转轴，与固定在铰接支座上的轴承动圈固结，见图8。

图8 实验设置Fig.8 Experimental setup

4.1 有限元模型修正

在结构损伤检测前，须建立与实验模型对应的健康结构有限元模型，由于建模存在误差需对初始有限元模型进行修正。具体模型修正见参考Chen等的研究。

4.2 损伤模拟与识别

修正后的有限元模型可以作为健康结构的基准来模拟损伤情况。如图9所示，通过减小梁的横截面来模拟结构损伤。通过降低梁刚度百分比来估计真实损伤程度。实验设置了4种损伤工况，见表3。切割位置选择在距离左端支座0.4 m和2.2 m处。真实的损伤程度通过惯性矩的变化近似估算，具体计算方法以及参数见Pan等的研究。从表3可知，频率随着损伤程度加剧而减小，本文选取前三阶测量频率与振型进行损伤识别。

采用ALO算法计算时，基本参数为：ALnum=100，Antnum=100，dim=10，Gmax=100，n=100，损伤因子约束在xi∈[0,0.99]。每个工况计算10次，取10次结果的平均值作为最终识别结果。

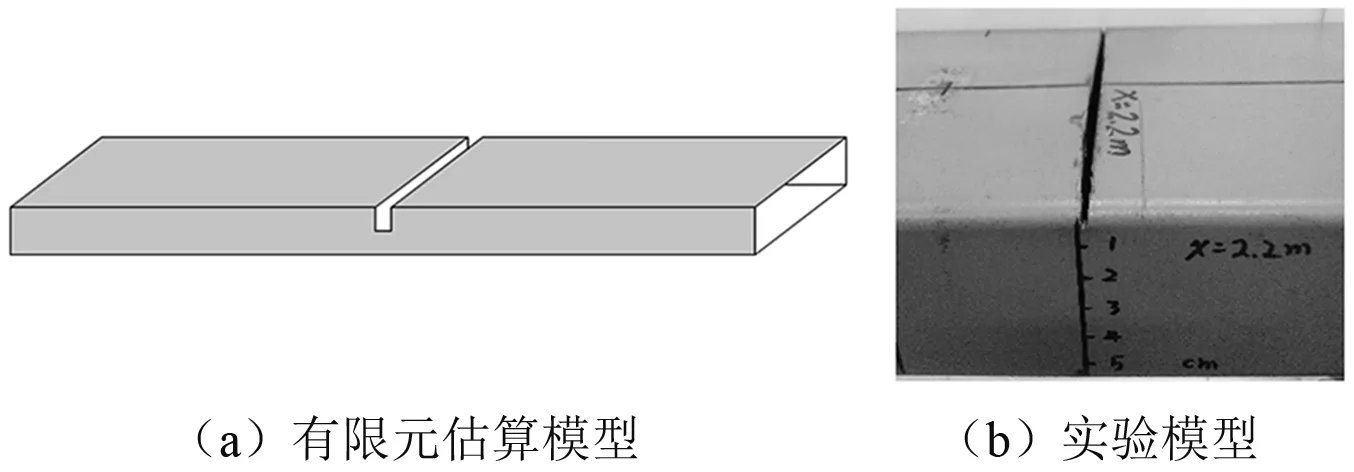
图9 实验切割模型Fig.9 Experimental cutting model

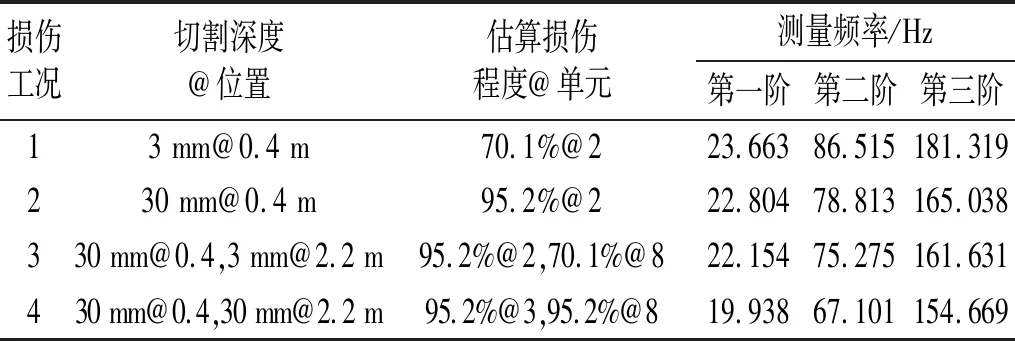
损伤工况切割深度@位置估算损伤程度@单元测量频率/Hz第一阶第二阶第三阶13 mm@0.4 m70.1%@223.66386.515181.319230 mm@0.4 m95.2%@222.80478.813165.038330 mm@0.4,3 mm@2.2 m95.2%@2,70.1%@822.15475.275161.631430 mm@0.4,30 mm@2.2 m95.2%@3,95.2%@819.93867.101154.669

由图10～图13的损伤识别结果可知：

(1) 本文所提方法在实验4个工况下都能够有效地定位损伤位置且准确识别损伤程度。虽然工况4中的5号和2号健康单元出现了较大的SDD值，但是与真实损伤单元SDD值比较，相对较小，所以能够从一定程度上仍能说明本文所提方法的合理性和有效性。

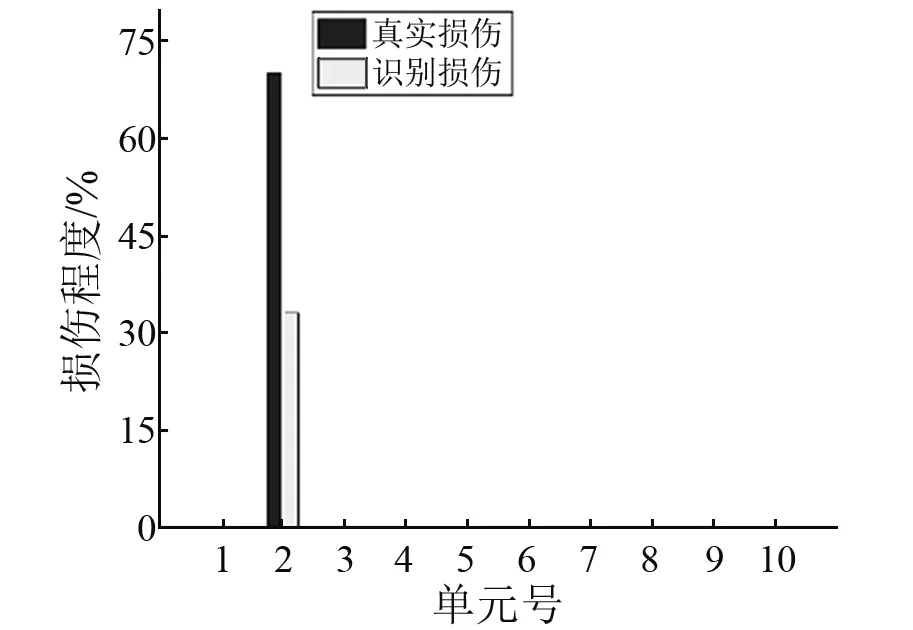
图10 工况1损伤识别结果Fig.10 SDD results in case 1

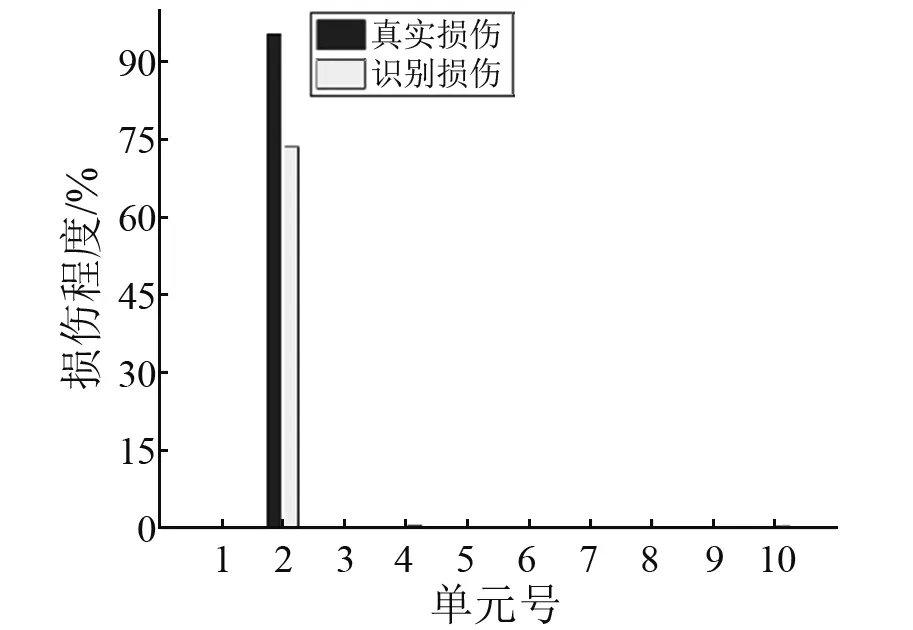
图11 工况2损伤识别结果Fig.11 SDD results in case 2

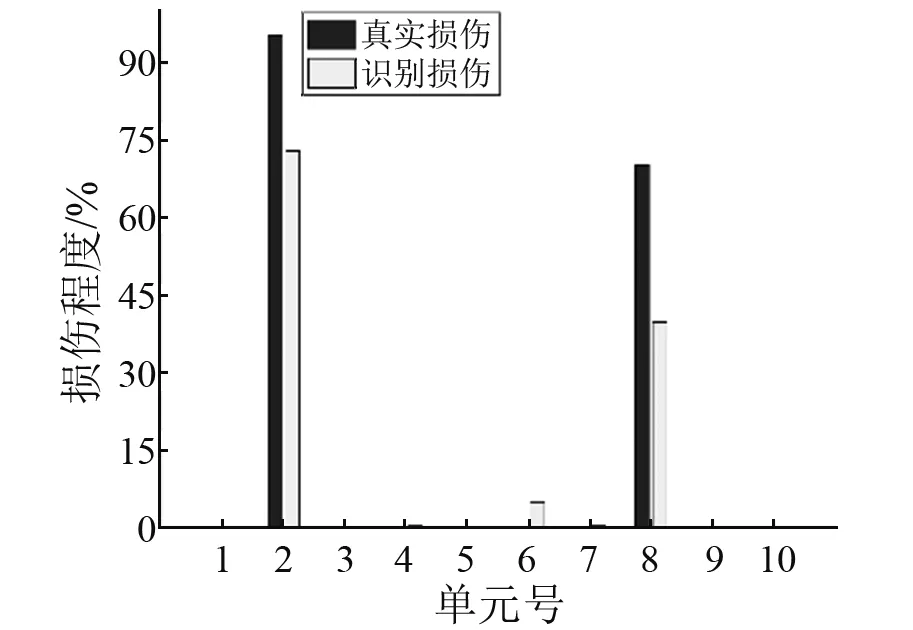
图12 工况3损伤识别结果Fig.12 SDD results in case 3

图13 工况4损伤识别结果Fig.13 SDD results in case 4

(2) 在2号和8号损伤单元上，损伤识别结果均要小于基于截面惯性矩变化的估算结果，主要原因是Lu等研究中所提损伤估算方法可能存在偏高估计。此外，从工况4的识别结果可以看出，2号单元和8号单元的损伤识别程度十分接近。因为两个单元内的切割缝深度相同，在一定程度上说明了损伤识别结果的合理性。

5 结 论

本文提出基于蚁狮优化算法和迹稀疏正则化的损伤识别方法。通对简支梁单损伤、两损伤、多损伤数值模拟以及钢管简支梁实验验证本文所提损伤识别方法的有效性和可行性。结论如下：

(1) 数值模拟与实验结果表明本文提出的基于蚁狮优化算法和迹稀疏正则化的损伤识别方法能够有效识别出不同损伤工况下的结构损伤位置及损伤程度，且具有一定噪声鲁棒性。

(2) 蚁狮优化算法各参数取值较合理，可应用于基于模型修正的结构损伤识别目标函数优化问题。

(3) 钢管简支梁模型修正结果表明，蚁狮优化算法修正的有限元模型能较好模拟实际模型。

(4) 真实损伤一般出现在结构局部位置，物理空间上具有稀疏性。在目标函数中添加稀疏约束有利于提取损伤识别结果的稀疏表示，既能抑制噪声带来的不利影响又能提高损伤识别精度。