钢管扣件式脚手架半刚性节点多参数模拟法

谢向阳，陈果，殷磊

(中国建筑工程(澳门)有限公司，澳门 999078)

随着计算机应用技术的发展，钢管扣件式脚手架的稳定承载性能研究逐步由以单排或整架实验数据为基础的长度系数修正法向计算机有限元模拟分析方法深入。在模拟分析中，立杆在节点处受水平杆、斜杆的约束刚度是最重要的基础性参数。立杆在节点处存在3个平动自由度(x,y,z)和3个转动自由度(x,y,z)，水平杆、斜杆针对这6个自由度的约束，有铰接、全刚性、半刚性3种假设模拟方法。

迄今为止，研究及实验工作主要集中在以扣件节点半刚性假设为基础的稳定性分析和对节点的转动刚度确定上。根据文献[1-6]，扣件节点半刚性的刚度研究基本集中在水平杆通过直角扣件对立杆在xz平面内的转动自由度y的约束刚度上，对其他5个自由度的研究较少，且研究主要集中在扣件本体抗滑及抗扭性能[7-9]。在已知的绝大多数稳定性分析中，采用仅y转动约束为半刚性的单一半刚性参数取值方案(以下简称“单参数”法)进行模拟及分析，除y转动约束外的其他5个约束均默认为铰接(3个平动全刚性、2个转动全释放)。以节点x平动约束为例，其刚度不到全刚性的4%(参见下文)，远达不到平动全刚性。因此，大多数以单参数节点半刚性假设稳定性分析研究在基础假设上存在不严密性。

在对架体稳定承载力中杆件作用机制初步分析基础上，采用敏感度分析方法，分析节点处全部6个自由度的约束情况与立杆特征值屈曲临界荷载系数(简称屈曲因子)之间的关系，判断每个约束各自的作用机制及贡献度。在已公开发表的实验测试数据基础上，分析实际约束刚度的取值区间，初步提出针对6个自由度节点约束刚度的多参数取值方案，并对节点约束、杆件的作用机制进行揭示阐述。

1 脚手架杆件作用机制初步分析

现行钢结构设计规范[10]中，压杆稳定承载力的计算与抗侧移刚度大小直接相关。设计简化脚手架模型并施加水平推力，观察架体侧移特征和内力特征，对架体的抗侧移机制进行初步分析。图1列出了在水平推力作用下4种形式的架体侧移状态，图2列出了无竖向斜杆(A类)和有竖向斜杆(B类)架体在水平推力下各杆件的内力情况。

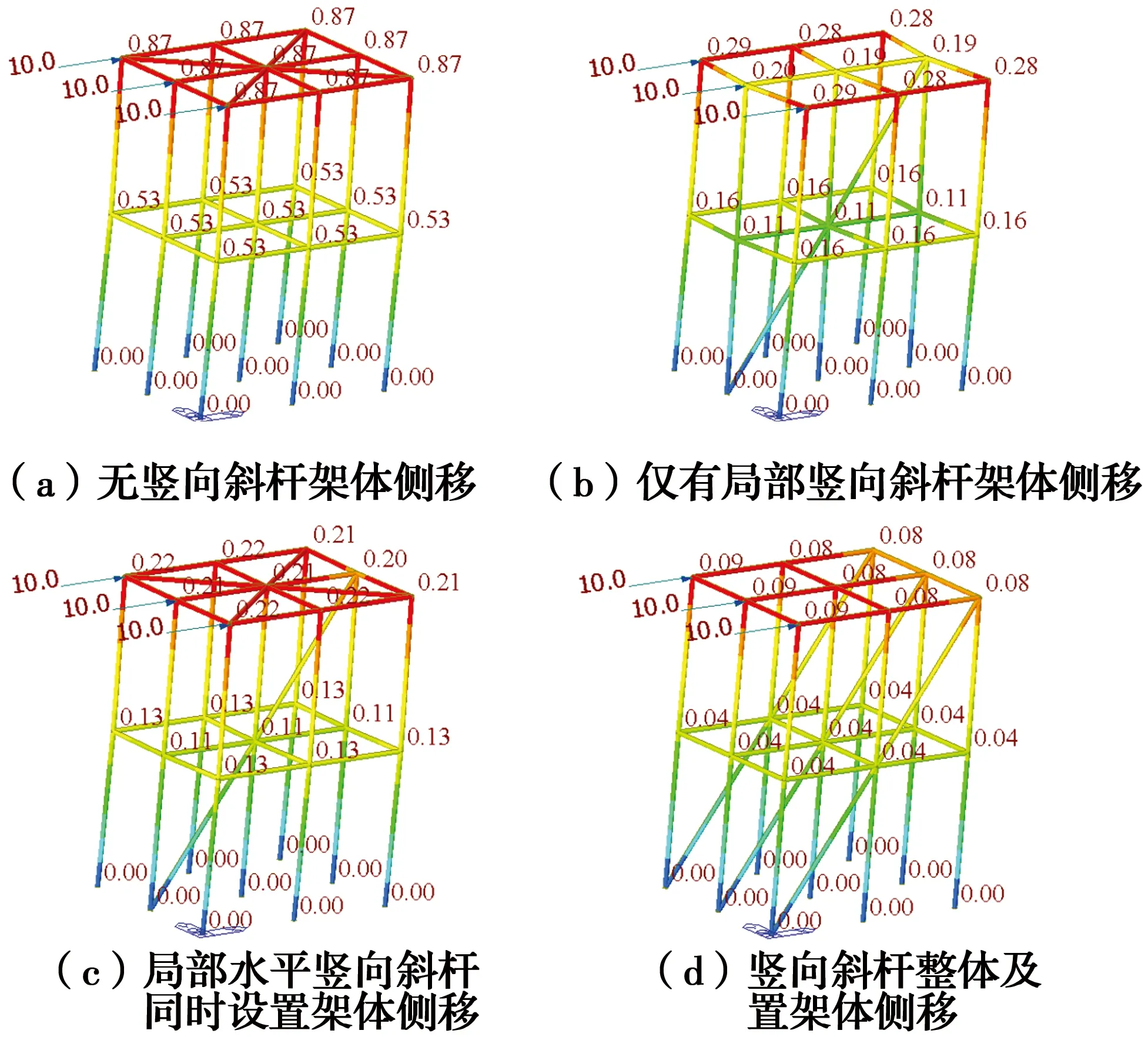
图1 水平推力下架体侧移状态示意图Fig.1 Displacement mode of frames under lateral

架体在无竖向斜杆的情况下(图1(a))，顶部侧移一致且侧移量最大；仅设置局部竖向斜杆无水平斜杆时(图1(b))，架体整体侧移量有较大幅度减少，同时，有竖向斜杆的刚架平面侧移量较其他无斜杆平面小；在设置局部竖向斜杆的同时设置水平斜杆时(图1(c))，架体整体侧移量进一步减少，刚架平面间侧移量差异缩小；竖向斜杆整体设置时(图1(d))，侧移量最小，且各刚架平面侧移一致。

当无竖向斜杆时(图2(a)～(c))，架体呈典型门式刚架侧移模态，水平杆弯矩Mz为0；当局部设置竖向斜杆时(图2(d)～(f))，轴力显著增大，My弯矩则减小，由于侧移量的不一致，水平杆出现Mz弯矩。在未列出的竖向斜杆整体布置架体模态中，My进一步减少，水平杆弯矩Mz为0。

图2 水平推力下架体内力状态示意图Fig.2 Inner force of frames under lateral

由以上分析可以初步看出脚手架杆件对架体抗侧移的作用机制：对于无竖向斜杆的架体，立杆和水平杆组成的门式刚架为抗侧移机构；当增加竖向斜杆时，斜杆与立杆、水平杆组成的三角形结构大幅度增强了抗侧移能力；架体内各片刚架侧移量不一致时，水平杆和水平斜杆提供一定的传递协同作用。

在对架体及杆件初步分析的基础上，展开对杆件及节点半刚性的具体分析。

2 节点半刚性对杆件刚度的折减机制

应用midas软件进行模拟分析计算，其全局坐标系z轴方向平行于重力加速度方向并与其反向；杆件通过扣件对立杆节点的约束，采用单元坐标系，x轴为杆件轴向。相关坐标系及约束释放符号规定如图3所示。

图3 坐标系及节点刚度符号规定Fig.3 Coordinate system and symbols of node

2.1 全刚接条件下水平杆对立杆约束的理论刚度

全刚性假设下，水平杆对立杆的约束刚度与杆件本身的物理性能及架体构造尺度相关。表1为基于Q235材质48 mm×3.2 mm钢管、1.0 m立杆纵横跨距构造的水平杆对立杆各平动、转动约束的全刚接条件下的理论刚度。

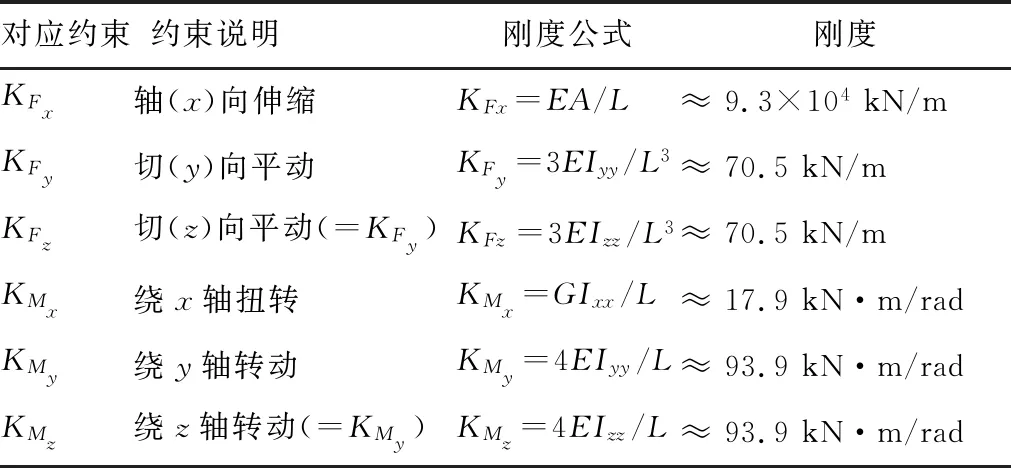
表1 全刚接约束条件下理论刚度计算表Table 1 Calculation table of stiffness coefficients under full rigid condition

注：表中，E=2.06×108kN/m2；A=4.50×10-4m2；L=1.0 m；Iyy=Izz=1.14×10-7m4；Ixx=2.27×10-7m4；G=7.9×107kN/m2。

2.2 扣件连接的各项节点刚度

脚手架实际构造中，水平杆通过直角扣件与立杆连接，节点受力后扣件与钢管壁之间存在滑移，扣件纵横扣之间存在转动。该滑移和转动，使得节点介于铰接和刚接之间的半刚性状态，因而，水平杆对立杆的各项理论刚度存在一定程度的折减。折减程度由扣件节点各项刚度决定，节点各项刚度及机制为：1)KjFx为轴(x)向伸缩节点刚度，由x向水平力作用下扣件沿水平杆轴向滑移距离确定，kN/m；2)KjFy为切(y)向平动节点刚度，由y向水平力作用下扣件的本体伸缩长度确定，kN/m；3)KjFz为切(z)向平动节点刚度，由z向水平力作用下扣件沿立杆轴向的滑移距离确定，kN/m；4)KjMx为绕x轴扭转度节点刚度，由扭矩作用下扣件绕水平杆轴向的滑动角度确定，kN·m/rad；5)KjMy为y向转动节点刚度，由在y向弯矩作用下扣件纵横扣之间转动角度确定，kN·m/rad；6)KjMz为z向转动节点刚度，由在z向弯矩作用下扣件绕立杆轴向的滑动角度确定，kN·m/rad。

2.3 扣件节点对理论刚度的折减系数

立杆通过直角扣件接受水平杆的约束，节点实际位移或转动情况与理论性全刚接时的节点位移转动情况存在差异。以节点z向平动约束为例，说明实际位移与理论位移、节点位移的关系。

假设水平杆与立杆为刚接、水平杆在节点处对立杆的约束刚度为KFz，则沿立杆轴向施加作用力P情况下，对应z向理论位移Δt=P/KFz(图4(a))。由于采用扣件连接，水平杆杆端处与立杆另存在附加的z向局部滑动位移Δj=P/KjFz，因此实际总位移Δ为Δt与Δj之和(图4(b))。实际总位移对应的全局总刚度以KgFz表示，则

Δ=P/KgFz=Δt+Δj=

P/KFz+P/KjFz

即KgFz= [KjFz/(KFz+KjFz)]×KFz

令i=[KjFz/(KFz+KjFz)]，则上式简化为

KgFz=i×KFz

式中的i作为系数，体现了由扣件连接弱于全刚接导致实际约束刚度相对于理论刚接刚度的折减程度，简称为刚度折减系数。节点其余各项约束的刚度折减系数同理类推，为对应节点刚度与理论刚度节点刚度之和的比值。在midas软件中，梁端(节点)约束的释放(半刚性)程度采用输入刚度折减系数来设定。

图4 理论与实际位移的关系示意图Fig.4 Schematic of relationship between theoretical

3 约束敏感度分析

为分析扣件连接点对立杆各项约束的效能，建立多个模型，运用单因素敏感度分析方法，确定扣件节点处6个约束项对立杆特征值屈曲的影响效能，从而研究约束的作用机制；同时，进一步展开对水平杆、斜杆作用机制和效能的分析研究。

3.1 敏感度分析的架体模型建立及设定

根据工程应用中较常见的架体构造参数，建立一个9.0 m × 9.0 m × 4.5 m的基准架体模型(模型1)：杆件为Q 235材质48 mm × 3.5 mm钢管，立杆纵横各9跨，纵横跨距1.0 m；纵横水平杆4道，步距1.5 m；边界条件为架体底部节点固定铰接；荷载条件为中部立杆顶端加垂直向下点荷载10 kN、边杆5 kN、角杆2.5 kN。在模型1的基础上，按表2所列方式增加斜杆设置，形成5个对比模型(模型2～6)。其中，模型4的构造示意参见图5。

表2 对比模型的构造Table 2 Construct of contrast models

图5 架体模型4构造图Fig.5 Construct schematic of model

3.2 约束敏感度测试方法及结果

通过逐一改变6个自由度约束项的刚度，测试承载能力变动的情况及规律，分析寻找其中对承载能力有重要影响力的约束项。

采用midas软件中的屈曲分析模块，进行架体特征值屈曲分析。水平杆与立杆相交节点处，6个自由度的基准约束均假设其刚度折减系数i=50%，对应屈曲因子λr作为本模型的基准屈曲因子。

针对以上所有模型，对于水平杆在节点处对立杆的每一项约束，在其他5个约束刚度均保持基准值不变的基础上，其刚度折减系数i依次取0.01%(相当于无约束，赋予其非0值以避免可能的矩阵奇异)、10%、50%、90%、100%，模拟扣件节点在该项约束上刚性的无、弱、中、强、全5种情况(基于表述的简洁性划分)，依次测试屈曲因子λi；通过分析屈曲因子比值R(λi/λr)的变动情况，研究架体稳定承载能力对该项约束变动的敏感程度。

实际扣件的约束能力和紧固程度有关，同一节点上，不会出现某单个约束项强而其他约束项弱的情况。因此，本步骤仅为针对约束项敏感度的理论性分析，而非实际扣件约束性能的分析。

所有模型的斜杆对节点的约束取值赋予初始值(取值情况在下文中说明)，并保持不变，以保证结果的可比性。敏感度测试结果见表3。

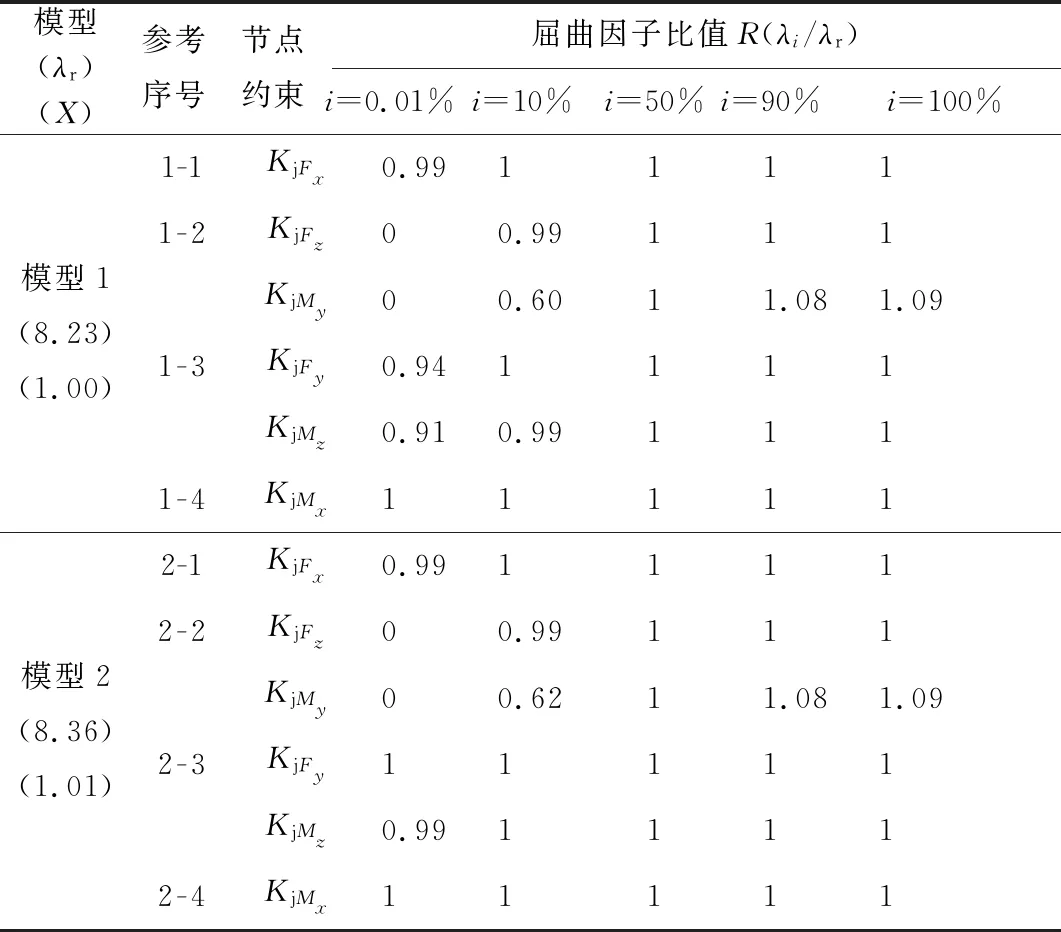
表3 各约束取值变化对应的屈曲因子比值R(λi/λr)Table 3 Ratios R of critical load factor on different assignments of each constraint

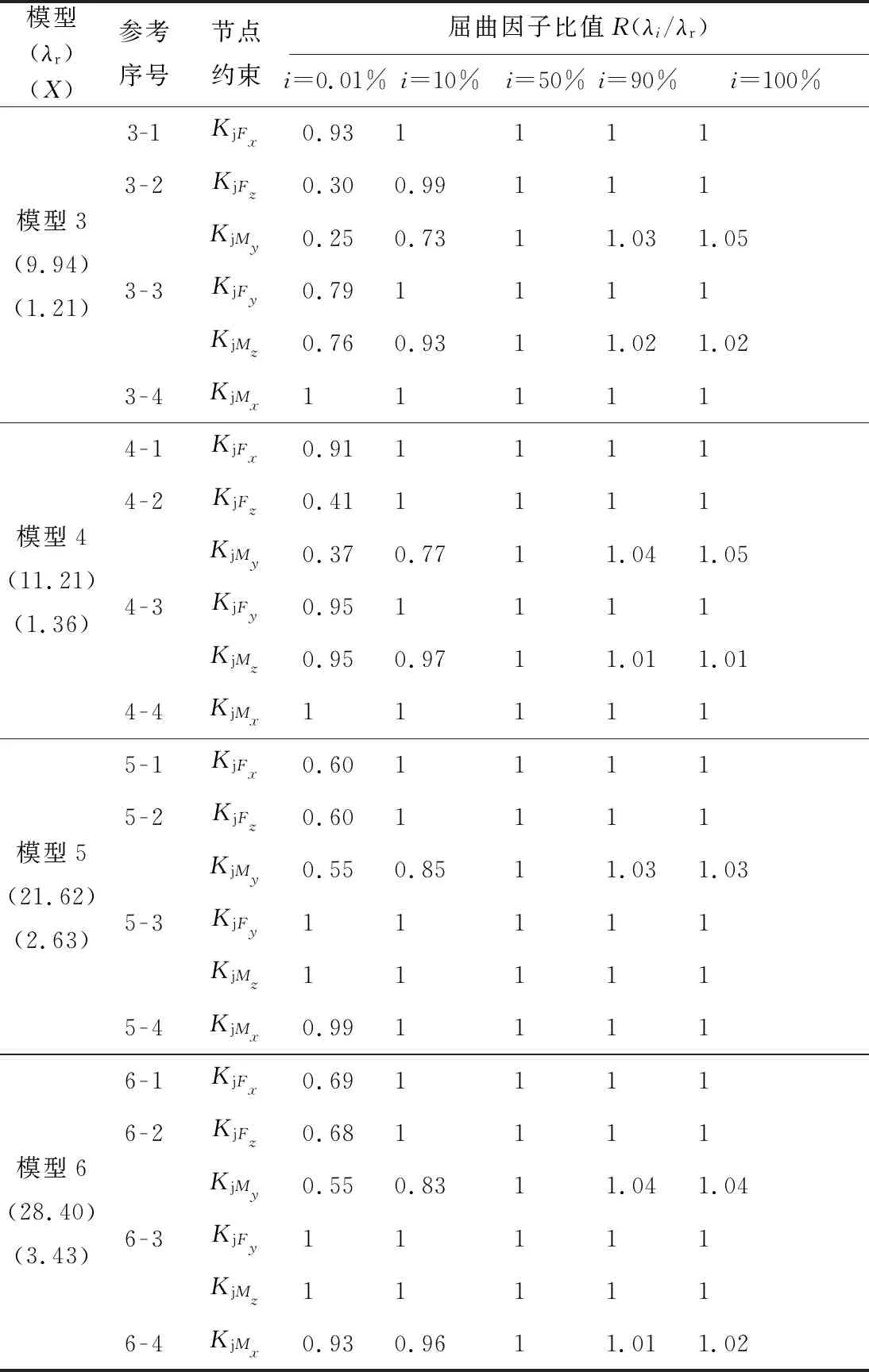
续表3

注：第一列中X代表本模型λr与模型1的λr的比值。

3.3 稳定承载能力对水平杆节点约束的敏感程度

表3表明，某项约束的刚度折减系数从0.01%增加至100%的过程中，如果屈曲因子比值R发生明显变化，则说明该模型的特征承载力与该约束有明显的相关性，即该约束产生效能贡献，反之则承载力不受该约束变化的影响，该约束不产生效能贡献。为便于表述，按R值变化情况，将承载能力对约束变化的敏感程度分为3个级别:不敏感(|R-1| ≤ 0.01，即从无约束到全刚性约束的整个变化过程中，承载能力变化小于等于1%)、弱敏感(0.01 < |R-1| ≤ 0.1)和强敏感(|R-1| > 0.1)。承载能力对各约束的敏感程度为：

1)KjFx：在无竖向斜杆时(参考序号1-1、2-1)，承载能力对该项约束不敏感(为简化表述，以下对 “承载能力对该项约束” 均做省略处理)；仅在四周配置竖向斜杆时弱敏感(3-1、4-1)；当竖向斜杆纵横满布时(5-1、6-1)，敏感度显著增强。

2)KjFz和KjMy：这2个约束存在明显的耦合性，且均表现出极强的敏感度；当无竖向斜杆(1-2、2-2)时敏感度最强，四周竖向斜杆(3-2、4-2)时次之，竖向斜杆纵横满布(5-2、6-2)时进一步降低。

3)KjFy和KjMz：这2个约束存在一定的关联性；仅存在水平斜杆(2-3)时或竖向斜杆纵横满布时(5-3、6-3)，均表现为不敏感；在无斜杆(1-3)时为弱敏感性，当四周配置竖向斜杆(局部性配置)(3-3、4-3)时，敏感度增强，但仍属弱敏感。

4)KjMx：仅在模型6中(6-4)存在弱敏感性，其余模型中均不敏感。所有模型中，仅模型6出现局部屈服模态，其他模型均为整体屈服模态。

3.4 杆件对架体承载力的效能贡献

表3中给出了各模型的基准屈曲因子λr及相关比值，由此可以看出：

1)仅增加水平斜杆，基本不产生效能。模型2的λr为模型1的1.01倍，即水平斜杆单独作用对稳定承载能力的效能贡献极低。

2)仅局部增加竖向斜杆，效能增加较明显。模型3的λr为基准模型的1.21倍。

3)在有局部竖向斜杆的前提下，设置水平斜杆能产生一定的效能。模型4在模型3基础上增加水平斜杆，λr为模型1的1.36倍。

4)竖向斜杆满设，效能远超过水平斜杆和局部竖向斜杆的组合方式。模型5的λr为基准的2.63倍。

模型6在模型5的基础上增加水平斜杆，λr为模型1的3.43倍。此时，模型6的屈曲已不同于模型5的整体屈曲模态，而是呈现局部屈曲，超出了作为大长细比结构脚手架的构造强度范畴，因而不做分析。

以上结果与脚手架杆件作用机制初步分析一致。

4 杆件约束作用机制及架体稳定承载力机制

4.1 水平杆各约束作用机制及效能

1)水平杆KjFz和KjMy(图2(b))为平面内抗侧移的一对约束。当无竖向斜杆时，其决定架体的特征值屈曲临界荷载(模型1、2)随着竖向斜杆设置增加(如模型3、4)，其决定作用降低；当全部配置竖向斜杆时，其作用进一步降低(如模型5、6)。

2)KjFy和KjMz(图2(c)、(f))为平面外抗侧移的一对约束。当竖向斜杆不设(模型1)或满布(模型5)时，不同架体竖向平面间的侧移基本一致，因此，这对约束仅显示极弱的效用(如边角荷载设定与中部荷载一致，则无效用)；当存在水平斜杆(模型2、4、6)时，水平斜杆与纵横水平杆组成的三角形结构对竖向平面间相对侧移的约束作用远强过这对约束，因而，其约束作用也相对微弱；在无水平斜杆且竖向斜杆局部布置(模型3)时，不同竖向平面间侧移不一致，因此，这对约束能产生一定的效用。

3)KjFx在没有配置或者少量配置竖向斜杆的模型中，由于竖向平面内立杆侧移形态基本一致，其作用微弱，随着竖向斜杆的增加，KjFx的作用逐步上升。KjFx的作用机制在于，其决定斜杆与立杆、水平杆组成的三角形抗侧移(图2(d))效能的大小，进而影响架体稳定承载力。

4)KjMx仅在水平杆发生扭转变形时产生约束作用。当架体平面间出现侧移不一致时，水平杆出现相对扭转，KjMx将约束这种扭转变形，但其约束远远弱于KjFz和KjMy的效能，更弱于斜杆的效能。因此，KjMx仅仅在构造非常强的模型6中出现了弱敏感性，而在模型1～5中均不敏感。

4.2 斜杆约束作用机制及效能

1) 竖向斜杆与同一竖向平面内的立杆、水平杆组成三角形结构，所提供的竖向平面抗侧移能力远超过仅由立杆、水平杆组成的门式结构。

2) 水平斜杆与纵横水平杆组成的水平三角形结构，在存在局部布置的竖向斜杆时，能将有斜杆的竖向平面抗侧移能力向无斜杆竖向平面传递，其传递效能远超过纵横水平杆组成的水平门式结构。

3) 当无竖向斜杆或竖向斜杆对称满布设置时，各竖向平面抗侧移性能一致，但由于边角部荷载较中部低，因此，局部侧移量不同，水平斜杆的存在仍能产生一定约束效能并少量提高架体的稳定承载力。

4.3 竖向斜杆局部配置的架体稳定承载力机制

竖向斜杆局部配置是指在架体纵横抗侧移刚架平面中，斜杆布置数量不同。这类架体的稳定承载力由架体中受步距层(水平杆层)约束最弱的立杆稳定承载力所决定。该立杆的承载能力由以下几部分综合决定：

1) 立杆所在xz或yz平面(无竖向斜杆的弱构造平面)本身基本抗侧移能力。其中，步距和立杆间距为其决定因素。

2) 立杆所在平面之外的强构造平面(配有竖向斜杆)抗侧移能力。其中，竖向斜杆配置量为该强构造平面的抗侧移的增量因素。

3) 外部强构造平面抗侧移能力通过水平斜杆KjFx约束(有足够配置时)或水平杆KjFy、KjMz约束(无水平斜杆或配置数量不足时)向本立杆所在弱平面传递的传递效能。

4.4 竖向斜杆整体配置架体稳定承载力机制

竖向斜杆整体均匀配置是指架体抗侧移刚架平面中，斜杆布置方式相同(无任何竖向斜杆配置属于本类型中的特例)。此类架体，由于各刚架平面抗侧移能力一致，其稳定承载力由立杆水平杆组成的门式刚架的抗侧移能力以及水平杆、立杆、竖向斜杆组成的三角形结构抗侧能力共同决定。

BS 5975—1996[11]的标准解决方案中，采用竖向斜杆整体均匀配置，无水平斜杆的概念及布置要求。

5 扣件节点刚度多参数模拟取值研究

根据扣件的传力特点和能力及有关文献的试验数据，结合前文的效能与敏感度分析，对扣件节点各项约束的局部刚度取值进行初步定量分析。

5.1 水平杆直角扣件节点各项刚度取值

1)扣件x向(轴向拉压)KjFx刚度，取决于扣件的水平抗滑性能；根据文献[7]提供的试验数据，直角扣件扣接下的P-Δl在2.1～6.5 kN/mm区间，其中，第1组数据为20 N·m拧紧力矩、4 kN加载幅度、周转25次情况下的初始刚度3.8 kN/mm。由于架体承受临界允许荷载时水平杆的拉压受力均未达到常规的8 kN抗滑允许值(参见后文)，综合文献中的加载幅度、周转次数、扭紧力矩等图表数据，暂定水平杆轴向节点拉压刚度为3 800 kN/m，则其对应i约为3.9%；该取值附近KjFx在常规构造形式(模型3～5)下均保持强敏感，即该取值的准确性对架体承载力分析的准确性影响更大。

2)扣件y向(切向)KjFy刚度，相当于扣件本体的抗拉压刚度(大于2×105kN/m)，远远大于杆件的KFy刚度。从表3可以看出，除竖向斜杆局部配置且无水平斜杆的模型3以外，其余模型KjFy均不敏感，因此，KjFy简化取值为全刚性，其对应i约为100%。

3)扣件z向(切向)KjFz刚度，其实际机制与KjFx一致，为扣件的抗滑移能力，约为2 100 ～6 500 kN/m，远远大于杆件的KjFz理论刚度70.5 kN/m，暂定取值为3 800 kN/m，其对应i约为98.2%；尽管总体上KjFz属于强敏感约束，但在这个取值的附近，KjFz已处于不敏感状态。

4)扣件绕x扭转KjMx刚度，取决于握裹水平管的扣件转动抗滑能力。这一方面的试验研究极少，朱启新等[4]在扣件节点的“水平面内的刚度测试”研究中提出，扭矩M<0.3 kN·m时，θ约等于0.084 7M，即KjMx约为11.8 kN·m/rad。暂定取整值12 kN·m/rad，其对应i约为40.1%；表3可知，i超过10%，除构造极强的模型6，其余常规模型中KjMx已不敏感。

5)扣件绕y轴转动KjMy刚度，取决于扣件的竖向平面内抗弯刚度。迄今为止，扣件对6个自由度约束绝大部分研究集中在KjMy的取值上。根据胡长明[2]的研究，标准拧紧力矩条件下，转动刚度试验值为85.96 kN·m/rad；袁雪霞等[1]的试验结果为46.85 kN·m/rad；根据朱启新等[4]试验研究结论，M≤0.4 kN·m时，θ约为0.044 3M，即刚度约为22.6 kN·m/rad；陈志华等[3]提出“在实际计算中,可以取拧紧力矩为40 N·m时的19.867 4 kN·m/rad作为扣件的转动刚度”。综合以上文献的试验设计严谨程度及实施先后关系，采纳陈志华等[3]的结论，并简化取整值为20 kN·m/rad，其对应的i约为17.6%。在该取值的附近区间，KjMy均保持强敏感，即该取值的准确性对架体稳定承载力分析，尤其是对无斜杆架体的准确性非常重要。这与Prabhakaran[12]的试验结论“对于有侧移框架而言，扣件未扣紧将显著降低承载力，而对于有斜杆框架影响相对较小”相吻合。

6)扣件绕z轴扭转KjMz刚度由扣在立杆部分的转动抗滑能力决定，与KjMx机制相同，暂定取值12 kN·m/rad，i约为11.3%。在该取值附近，对于模型3的构造方式，KjMz处于强敏感状态，其余构造方式则处于不敏感状态。

5.2 斜杆旋转扣件节点各项刚度取值

斜杆的主要贡献在于形成稳定三角形所提供的抗侧移能力，即KjFx起决定作用；针对斜杆其他约束项的作用，由于实际工况中斜杆配置数量远低于水平杆，因此，贡献作用微弱。在郑莲琼等[8]的周转性试验数据中，旋转扣件KjFx初始值的区间为600～2 000 kN/m，剔除极端情况下的偏保守取值为1 500 kN/m。

竖向斜杆与立杆采用旋转扣件连接，不提供y向转动约束，因此，KjMy=0；竖向斜杆的其余约束项机制基本与直角扣件相近，且效用极低，因此，KjFy、KjFz、KjMx、KjMz取值参照直角扣件的约束假设。

水平斜杆与水平杆采用旋转扣件连接，不提供z向转动约束，因此KjMz=0；水平斜杆的其余约束项机制基本与直角扣件相近，参照直角扣件的约束假设，由于β角的不同，水平斜杆的KjMy、KjMz分别与竖向斜杆的KjMz、KjMy相等。

5.3 扣件刚度多参数法及分析

扣件刚度多参数法模拟方案见表4。在表4基础上，再次采用敏感度分析方法，选择较典型的模型4作为基准，在其他约束不变的基础上，将每一约束取值乘以0.5～1.5的系数进行单独弱化和强化，测试其λi与标准取值方案下λr的比值，以判断约束取值的容错性能，结果见表5。

表4 扣件刚度多参数法Table 4 Coupler stiffness value multi simulation scheme

注：表中“/”代表全刚接。

表5 模型4在不同约束取值系数下的屈曲因子比值RTable 5 Ratio R of critical load factor under different value factors of constrain of model 4

注：A代表水平杆+直角扣件；B代表竖向斜杆+旋转扣件；C代表水平斜杆+旋转扣件。篇幅所限，仅列出比值R最大变动超过0.01的约束项。

由表5可以看出，影响模型4临界荷载值的关键因素在于水平杆直角扣件节点的KjMy刚度和斜杆旋转扣件节点的KjFx刚度；在未列出的针对模型6的测试中，水平斜杆所有约束已无敏感性，即不起作用。以上数据及分析体现以下两方面的意义：

1)在更准确的模拟方式下，仍体现了前面各部分分析的基本特点。在全部平面同等竖向斜杆配置情况下，各平面抗侧移能力基本相等，水平斜杆因不需协调强弱平面而不产生效能。在局部平面配置斜杆的情况下，水平杆及竖向斜杆的KjFx显著影响竖向斜杆所在平面的抗侧移能力，水平杆的KjFz及KjMy决定无竖向斜杆平面的基本抗侧移能力，水平杆及水平斜杆的KjFx决定强弱平面间的效能传递效率。

2)当以上关键约束项的刚度取值同时出现一定程度的偏差(±50%)时，特征值将出现大的偏差。在未列出的进一步分析中，当将所有约束刚度取值同步降低50%和增加50%进行计算，后者的特征值约是前者的2.1倍，差异幅度较大，而作为取值基准参考的部分文献刚度试验数据之间的差异已经超过上述假设值的差距。因此，对关键约束项刚度取值进行针对性的系统实验研究，是脚手架稳定承载力分析计算得以准确深入开展的基础。

5.4 扣件刚度多参数取值方案的简化

根据表4、表5的数据，将不敏感的约束项进一步简化，并与常规取值方案进行对比，见表6。

KjMz(11.3%)尽管在表5的变动区间(6.0%～16.1%)内属于不敏感约束，但如简化为0或100%，其他模型结果会出现一定偏差(表2的模型3、模型4)，因此，KjMz刚度不做简化。

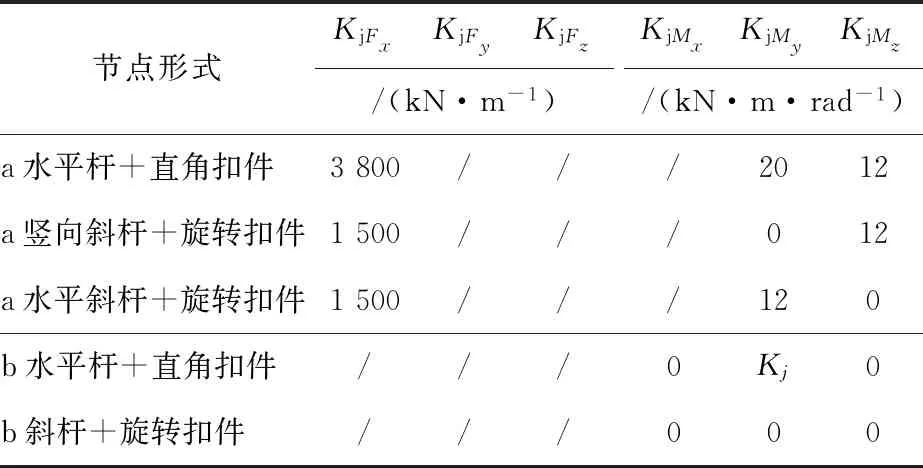
表6 节点刚度取值方案对比Table 6 Comparison of node stiffness value schemes

注：1.表中“/”代表全刚接；a代表多参数方法，b代表单参数方法；
2.“Kj”表示有关单参数方法的KjMy取值，范围为19～90kN·m/rad。

6 多参数模拟法的前提条件验证

在确定扣件节点各项约束取值时，基本依据是有关参考文献的试验及分析数据，该数据源于试验中的加载条件。因此，必须对扣件在架体承受最大允许荷载时的实际受力状态与有关试验的加载力进行对比，以确定约束刚度假设值的前提条件是否达到。

如表7所示，构建纵横15跨(跨距1 m、长宽15 m×15 m)、20步(步距1.5 m)、顶底分别挑出0.5、0.3 m(架体总高30.8 m)的2个对比模型，模型7-a按照《建筑施工扣件式钢管脚手架安全技术规范》(JGJ 130—2011)[13]中剪刀撑普通型要求构造，模型7-b按照竖向斜杆整体平均布置构造，其他构造参数参照前面模型，约束假设采用多参数法。通过特征值屈曲分析，获得架体的临界荷载，推算出名义计算长度，按照JGJ 130—2011的稳定系数表，计算出最大允许荷载值作为设计荷载，采用midas的P-Delta模块进行(几何非线性/材料线弹性)二阶分析，获得极限性荷载条件下2个架体构件节点内力(即扣件受力)的基本情况。

表7 对比模型组构造Table 7 Construct of contrast model group

注：1.名义计算长度为立杆的计算长度最大值，根据架体特征值屈曲临界荷载及欧拉稳定公式计算得出；
2.设计承载力系根据名义计算长度、按照JGJ 130—2011的稳定系数表计算得出。

二阶分析中的初始缺陷考虑架体的整体搭设缺陷Δ和杆件的初始缺陷δ。

整体搭设缺陷的设定上，对比第1阶特征值屈曲模态缺陷构型法、假想力法、缺陷直接构型(一致偏移)法后，最终选择更适合脚手架承力构造特点的缺陷直接构形法，按照总高3/1 000的允许搭设偏差进行整体一致偏移，完成Δ的设定。

杆件的初始缺陷值根据JGJ 130—2011中允许的偏差标准，6.5 m杆件杆中不大于20 mm、顶部挑出杆件杆顶偏移小于5 mm进行设定，采用一致偏移构形法设定整体搭设缺陷后，取其第1阶特征值屈曲模态，并根据其波长情况，依据6.5 m内不大于20 mm 的基本比例设定最大值初始缺陷值，对模型进行更新，完成δ设定。几何非线性分析结果见表8。

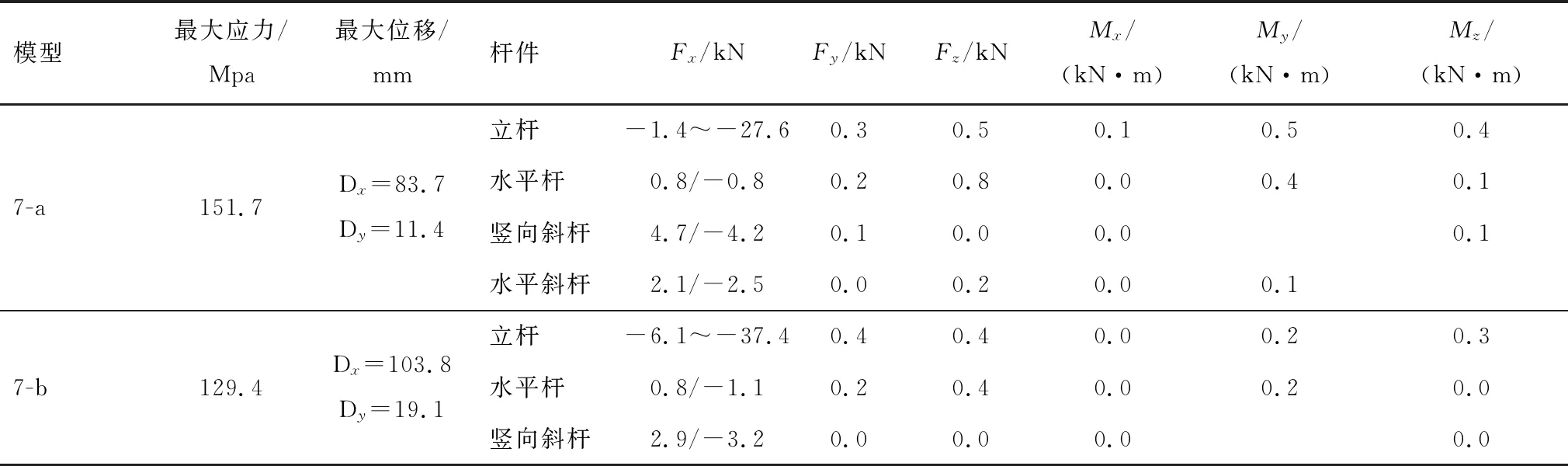
表8 对比模型组的位移及杆件内力Table 8 Displacement and tube internal force of contrast model group

注：Fx中正值代表拉力，负值代表压力。

由表7数据可知，直角扣件、旋转扣件水平抗滑承载Fx最大值分别为1.1和4.7 kN，均未超出规范允许承载力8 kN以及文献[7-8]采用的4～12 kN的试验加载值范围，因此，扣件节点平动刚度的取值条件得到验证；直角扣件、旋转扣件旋转抗滑承载Mz最大值为0.1 kN·m，未超出文献[4]中M<0.3 kN·m的取值条件，其对应转动刚度取值条件得到验证；直角扣件竖向平面内抗转动承载My最大值为0.4 kN·m，未超过文献[3]中0.2 ～ 0.8 kN·m的试验加载范围。另外，由于模型构建时，模型中的杆件均简化为交于同一节点，而实际存在最少2个甚至6个以上扣接点，节点间的规范最大允许间距达150 mm。因此，上述简化对节点受力主要是直角扣件竖向平面内抗弯存在一定影响，但通过对附加弯矩、附加应力的测算，在较不利情况下，节点受力仍处于文献[3]的试验加载范围内。

通过以上计算，分析架体扣件节点的受力状况，均未超出多参数模拟法所参照相关文献的试验加载条件，多参数模拟法的前提条件得到验证。

7 常规取值方案及部分模型假设问题

7.1 常规方案的特征值偏大

常规单参数法半刚性假设见表6，平动约束均采用全刚性(铰接)假设，转动约束KjMx、KjMz为0，转动约束KjMy采用水平杆与立杆(直角扣件)连接条件下的竖向平面转动线性刚度Kj。其与多参数取值简化方案的关键区别在于KjFx的取值，其次在于KjMz的取值。

按照现行规范JGJ 130—2011有关加强型剪刀撑的配置要求建立模型8(有关杆件参数同模型1)，见图6。立杆间距1 m共12跨、长宽各12 m，水平杆步距1.5 m共12跨、总高18 m；竖向剪刀撑平面纵横每4跨设置，平面内斜杆配置率(有斜杆的框格占总框格的比率)为1/2；水平剪刀撑每四步(间隔6 m)一设、平面内斜杆配置率1/2。以模型8为基准，按照表9中的构造变化形成对比模型组，分别按照表6的两种取值方案，对模型的特征值进行计算，特征值结果对比见表10。

表10结果充分体现了常规方案将节点的KjFx设置为铰接(平动全刚性)，所造成强构造平面抗侧移能力的高估，进而导致架体稳定承载能力高估；尤其对于8-f、8-g两个模型，单参数法的结果为多参数方案的2.5倍左右。可见，半刚性单参数法在关键性假设上仍为平动全刚性，因此结果偏大。这也是有关文献模拟计算结果和规范允许取值之间存在巨大差别的原因之一。另外，表10表明，不同竖向斜杆设置构造，模型特征值差别较大，最大值约为最小值的2倍多，约为无竖向斜杆设置模型的3.5倍(未列出)。文献[14]中的试验验证了双排脚手架横向设置斜杆对承载力有1.6倍的提升，破坏发生在未设斜杆的纵向杆；但文献 [15]中采用单一的1.4倍系数确定设剪刀撑情况下承载力的调增，难以体现不同剪刀撑设置方式对承载能力的巨大影响差异。

图6 模型8构造示意图Fig.6 Schematic construct of model

模型竖向斜杆平面间隔(纵横)竖向斜杆配置率水平斜杆层间隔水平斜杆配置率84跨1/24步1/28-a4跨1/34步1/28-b4跨1/64步1/28-c4跨1/124步1/28-d4跨1/24步1/68-e4跨1/64步1/68-f每跨1/64步1/68-g每跨1/6不设0

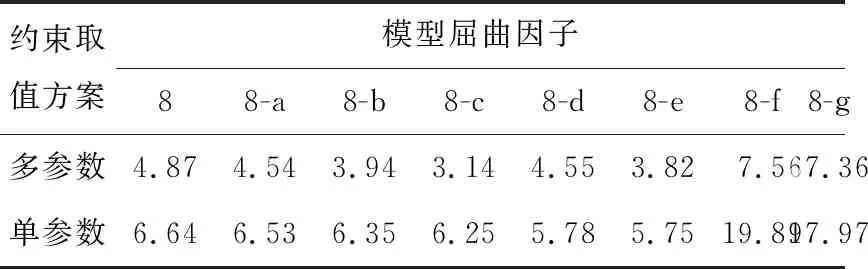
表10 两种取值方案下屈曲因子对比表Table 10 Critical load factor comparison between two value schemes

7.2 水平斜杆效用分析的误区

部分文献对水平斜杆的效用分析容易造成误导，即认为水平斜杆能较大程度地直接提高架体承载能力。相关规范指导也认为，水平斜杆是提高架体稳定性的必要措施。

从前文分析可知，水平斜杆的效能主要是传递作用。当无斜杆或整体配置斜杆时，水平斜杆基本不发生作用；即使在竖向斜杆局部配置的情况下，当水平斜杆配置层的间隔偏大，其效能贡献较低。

对于模型8，采用多参数法，增减水平斜杆层的布置，与完全无水平斜杆进行对比；另外，通过仅增、减立杆钢管壁厚来模拟基准架体的立杆计算长度的变化，增加两组对比参考数据。计算结果见表11。

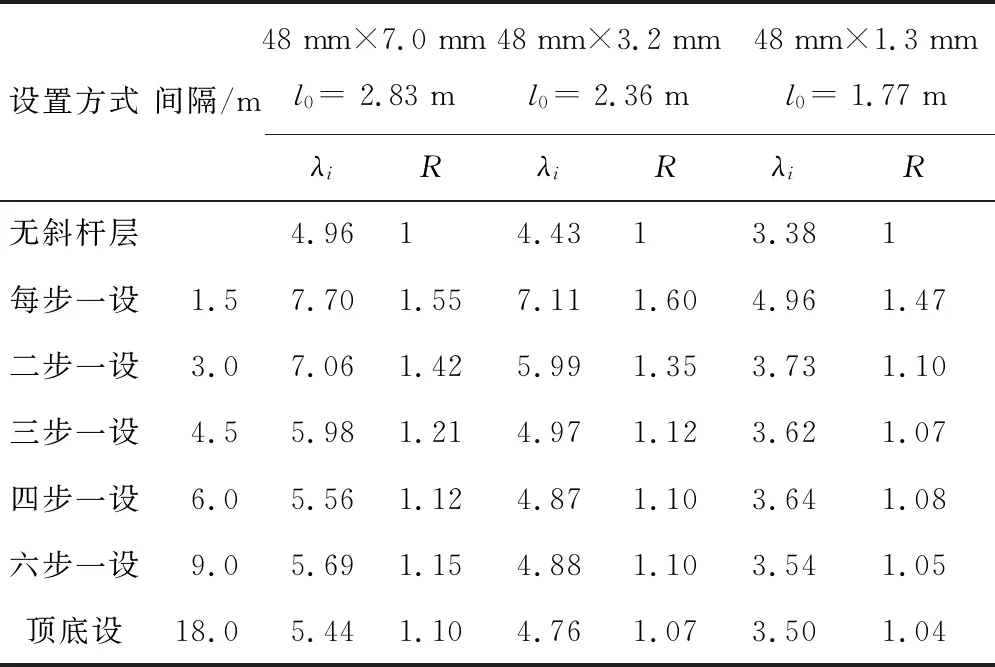
表11 不同水平斜杆层间隔设置及不同截面立杆的屈曲因子及比值Table 11 Eigenvalue and ratio of different set-up of horizontal level inclined brace layer and upright tube sectional dimension

注：l0为无水平斜杆层模型立杆的最大计算长度，根据特征值屈曲临界荷载及欧拉稳定公式计算得出。

从表11中可知，对于48 mm×3.2 mm立杆，符合规范剪刀撑加强型构造标准四步一设(≤ 6.0 m)的水平斜杆层，只产生约10%的贡献，在实际中基本不可能采用两步一设的条件下才有显著贡献；另外两组数据规律相同，且显示出基准模型计算长度越短要求水平斜杆层的间隔越小，才能产生同能效能贡献。

在未列出的另一组测试中，在模型8的基础上，每步一设水平斜杆层(R=1.6)，如将竖向斜杆配置率由1/2降为1/6时，R迅速降至1.2，如继续将每层水平斜杆配置率降为1/6，R为1.1。

因此，仅当存在局部平面配置较强的竖向斜杆，且当水平斜杆层的间隔距离接近立杆的计算长度(如两步一设)时，水平斜杆将产生显著的效能；当超过2倍计算长度时(如规范所规定的四步一设)，实际效能较低。

常规四步一设的水平斜杆，在仅有局部少量竖向斜杆的条件下，其真实作用远低于通常的估计或推断。

7.3 局部加载的整架试验可能存在的结论失真问题

部分文献中，如文献[15]，采用了局部加载的方式进行整架试验。架体局部承载时，未承载区域架体仍将提供竖向平面的抗侧移效能，而计算分析时，一般都将这部分效能归于承载区域的架体立杆，按此立杆推算架体整体状态，即会导致节点约束刚度及架体承载力的高估以及架体承载状态的误判。

如图7所示，按照文献[16]中工况3的模型参数，当采用局部承载时，承载立杆的临界荷载将大于整体承载条件的临界荷载，如采用该临界荷载来推算架体所有立杆的能力，即会导致高估；满载屈曲模态为正常的宽度方向屈曲(图7(a))，而局部加载的模态为长度方向的屈曲(图7(b))，二者模态完全不同。

如水平杆和斜杆按铰接进行假设计算，承载能力计算结果将偏高(偏差程度与斜杆配置数量有关)，而采用局部加载进行整架试验，最终试验结论也将出现高估，因此，难以发现计算假设中的缺陷。

图7 满载与局部加载模态对比示意图Fig.7 Comparison mode diagram of whole loading

8 结论

1)扣件式钢管脚手架的承载力取决于架体弱构造平面立杆的承载力；该平面立杆的承载力由平面自身抗侧移能力以及强构造平面传递而来的抗侧移能力决定；在无斜杆配置的架体内，平面自身抗侧移能力由水平杆及直角扣件提供的KjMy、KjFz两项平面内约束所决定；在有斜杆配置的架体内，竖向斜杆的数量显著影响强构造平面的抗侧移能力，水平斜杆的KjMz、KjFy形成一定强弱平面间抗侧移能力的传递作用，水平斜杆的间隔层数及配置数量，决定强弱平面间抗侧移能力传递能力。

2)通过约束的敏感度分析，在已知实验数据的基础上，提出了针对水平杆、斜杆及直角扣件、旋转扣件的节点约束多参数模拟方法。

3)通过应用多参数模拟方法以及二阶分析方法，计算架体水平杆、斜杆的内力状况，间接获得了扣件的受力状况。计算结果表明，扣件受力基本处于相关试验的加载区间内，初步复核验证了多参数模拟方法的可靠度。同时，计算结果也间接证明了架体压溃属于立杆失稳性压溃，而不是节点强度性压溃。在架体(极值)破坏之前的临界平衡阶段，节点处扣件受力很小，只有在临界平衡被打破后，架体发生大幅度变形，之后导致节点受力急剧增大，最终扣件破坏或失效。

4)将水平杆、斜杆的三向平动约束假设为全刚性的常规假设方法、以及部分模型的不当假设，会导致对架体承载能力的高估，同时也会影响到架体承载机制及效能研究工作的方向。

关于约束的作用机制，多参数模拟法的研究结果显示，在钢管扣件式脚手架稳定承载能力研究中，节点半刚性单参数法存在基础性的缺陷，采用多参数法较之于单参数法，能进行更清晰、全面、准确的分析度量研究。今后如能基于约束作用机制，对全部节点约束进行针对性、系统性的扣件试验和整架试验，将为脚手架稳定承载能力研究提供关键性参考。