基于无应力状态量的平面梁节段预制构形计算方法
但启联,秦顺全,2,魏凯,邓鹏,苑仁安,2
(1.西南交通大学 土木工程学院,成都 610031;2.中铁大桥勘测设计院集团有限公司,武汉 430050)
预制节段施工方法[1-3]是将梁体分为若干节段,在工厂或工地附近制梁场预制后,在桥位处进行组拼形成桥梁的一种施工方法,该方法经济、环保、高效,节段便于工厂化生产,质量易于控制,在现代桥梁施工中被广泛采用。采用预制节段施工方法的关键是确定并精确制造出能满足主梁线形的所有梁段。对于主梁节段预制,常用的方法有长线法[4-5]和短线法[6-9]。长线法是按设计的制梁线形制作固定曲线底座,预制节段在该固定底座上逐段生成,由于各节段间的相对几何关系由底座曲线确定,精度易于控制。该方法对台座稳定性和预制施工场地要求较高。短线法是在同一可调支架上逐段制造所有梁段的方法,它以已完成预制的相邻节段一端作为端模,通过调整与端模的角度实现预制节段的线形,制造梁段的线形在与已成梁段的匹配中实现,其精度主要取决于线形的调整精度。长线法和短线法制造梁段前需准确计算主梁的制造线形,以使梁段在组拼后满足主梁设计线形要求。
近年来,有学者基于无应力状态控制法,对预制节段施工主梁节段制造和安装问题展开了研究。余昆等[10]针对钢箱梁斜拉桥悬臂拼装施工线形控制问题,提出基于无应力状态法理论的主梁线形控制的方法,通过主梁制造线形推算梁段间相对几何关系,用以指导梁段的制造和安装,使最终成桥状态内力和线形满足目标要求。吴运宏等[11]针对钢箱梁斜拉桥主梁线形控制问题,提出考虑内力修正的主梁节段预制尺寸确定方法。颜东煌等[12]基于自适应无应力构形控制思想,推导了主梁节段轴线夹角及节段制造参数公式。以上方法在确定节段预制构形时,均需事先获得主梁制造线形,由制造线形通过几何递推确定梁段间相对几何关系和梁段预制参数,过程较繁琐。
无应力状态控制法理论[13-15]阐明了结构施工过程与最终成形状态之间的关系,指出分阶段施工桥梁控制的核心是构建单元无应力状态量。单元无应力状态量是结构单元本身的稳定固有量,表征了单元无应力时的几何尺寸和形状,将其回归到单元预制构形确定,并用以指导节段的预制施工,具有工程实际意义。文献[16]建立了基于平面梁单元的分阶段成形结构线形控制方程,由方程可直接求解结构单元无应力状态量。若要用单元无应力状态量来确定单元预制构形,需首先明确二者间的对应关系。笔者通过对矩形平面梁单元变形过程分析,建立单元无应力状态量与预制构形参数间的数学关系,并通过数值算例对关系式进行验证。
1 平面梁节段预制构形计算理论
由有限元分析理论可知,节点位移下单元形状和尺寸将发生改变。通过分析平面梁单元在节点位移下的变形来建立单元无应力状态量与单元预制构形参数间的关系。对矩形平面梁单元,发生节点位移后,单元两端面曲率和长度为
(1)
l′=l+uj-ui
(2)
式中:ui、uj分别为单元i、j端的轴向位移;vi、vj分别为单元i、j端的横向位移;θi、θj分别为单元i、j端的转角位移;l为单元的初始长度。
为方便分析,规定单元构形夹角为单元两节点连线与单元端面内法线的夹角,记为θi0、θj0,并规定连线顺时针转向内法线时的夹角为正,反之为负[16]。单元构形长度为单元节点间的几何距离,记为l0。为了方便梁段的制造,工程中常采用以直代曲的方式将曲线形梁段简化为直线形梁段,文中单元构形均指直线形构形,但无应力状态量仍指曲线形梁段单元对应的无应力状态量,单元无应力构形见图1。
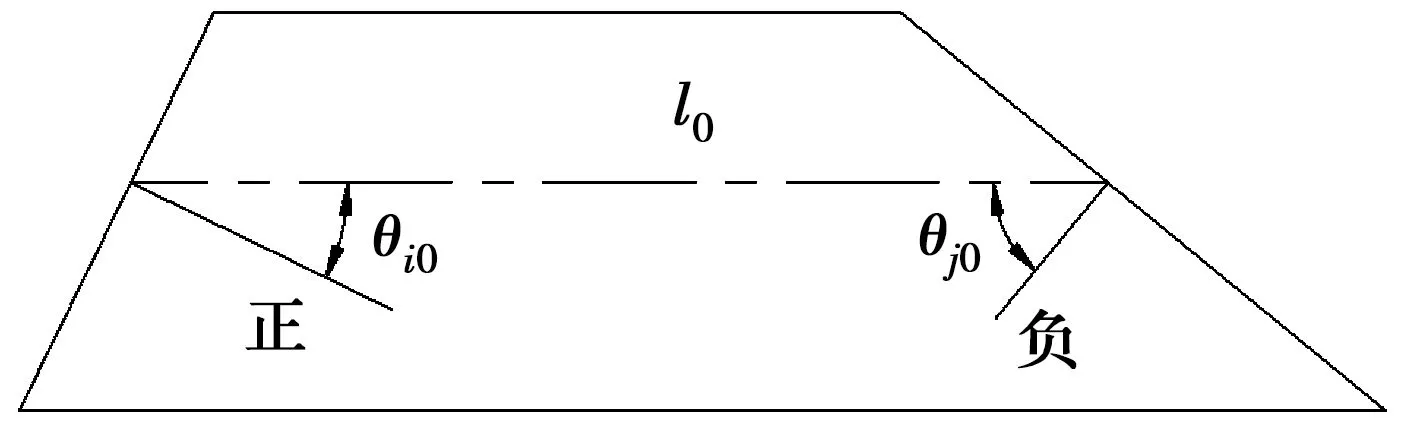
图1 平面梁单元预制构形Fig.1 Precast configuration of plane beam
1.1 无应力曲率与预制构形夹角
在节点转角位移或横向位移下,平面梁单元将产生弯曲变形,分3种情况讨论。
1)节点产生转角位移
单元仅产生节点转角位移θi、θj,无横向位移,如图2所示。单元两端截面产生相对转动,变形后单元构形夹角为
(3)
代入式(1)得变形后单元端面无应力曲率为
(4)
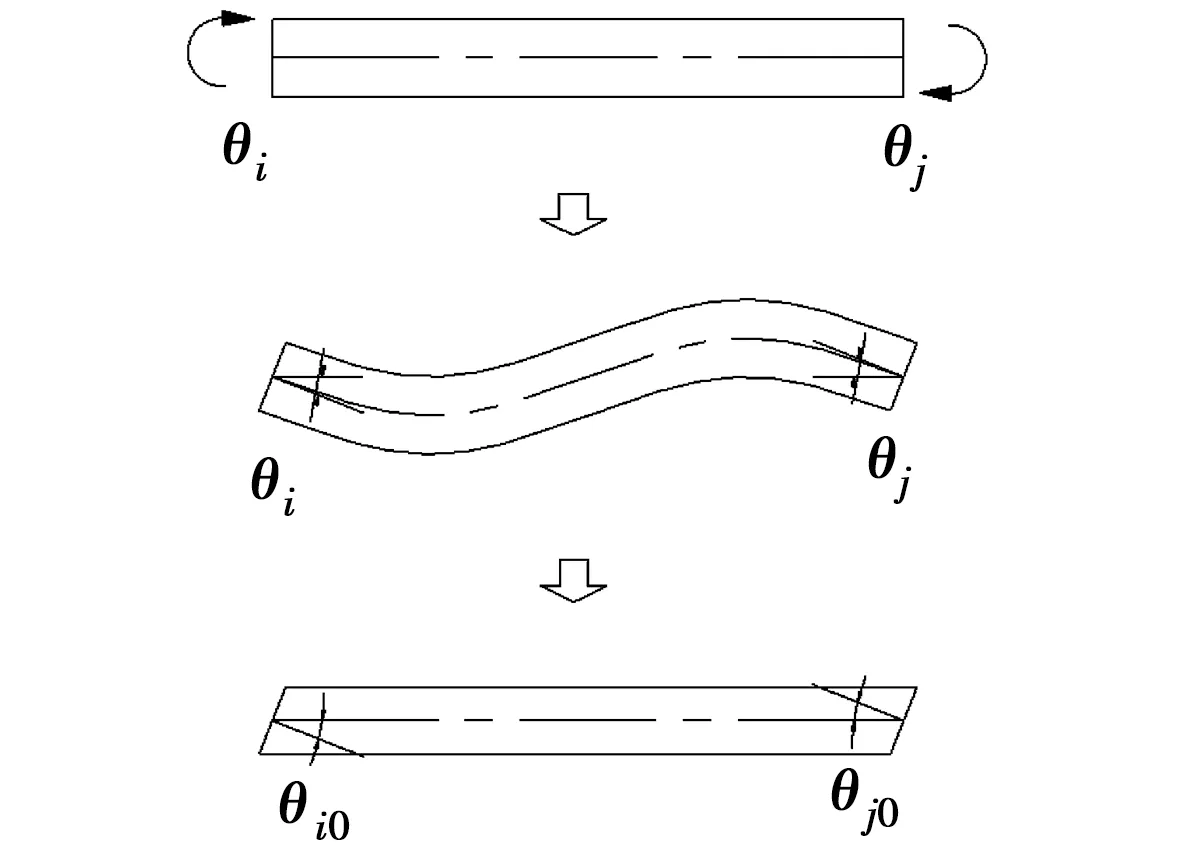
图2 单元节点产生转角位移Fig.2 Angular displacement occurring on the element
2)节点产生横向位移
单元仅产生节点横向位移vi、vj,无转角位移,如图3所示。单元两端面产生相对错动,变形后单元构形夹角为
(5)
代入式(1),考虑与式(4)形式上的统一,得变形后单元端面无应力曲率为
(6)
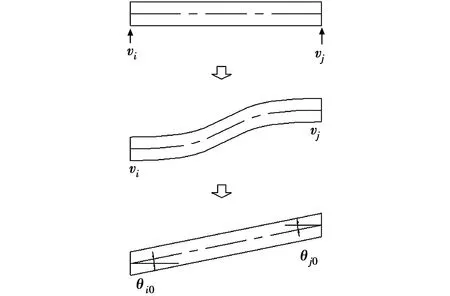
图3 单元节点产生横向位移Fig.3 Transverse displacement occurring on the element
3)节点产生横向位移和转角位移
单元同时产生节点横向位移vi、vj和转角位移θi、θj,如图4所示。此时,可看作情况1)、2)的叠加,变形后单元构形夹角为
(7)
代入式(1)得变形后单元端面无应力曲率为
(8)
式(4)、式(6)、式(8)的形式一致,说明无应力曲率与单元构形夹角对应。由式(4)、式(6)、式(8)的任何一个,容易导出用端面曲率表示的构形夹角的表达式,即
(9)
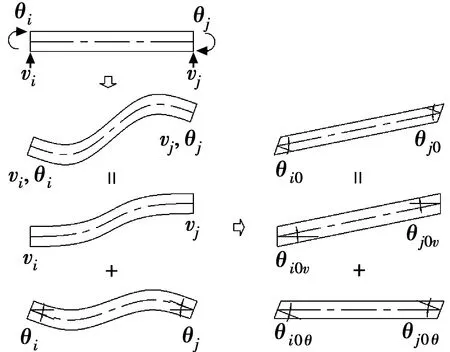
图4 单元产生横向位移和转角位移Fig.4 Both of angular and transverse displacements occurring on the element
1.2 无应力长度与预制构形长度
单元仅产生节点轴向位移ui、uj,如图5所示。单元将产生长度改变,改变量为
Δl=uj-ui
(10)
变形后单元构形长度为
l0=l+Δl
(11)
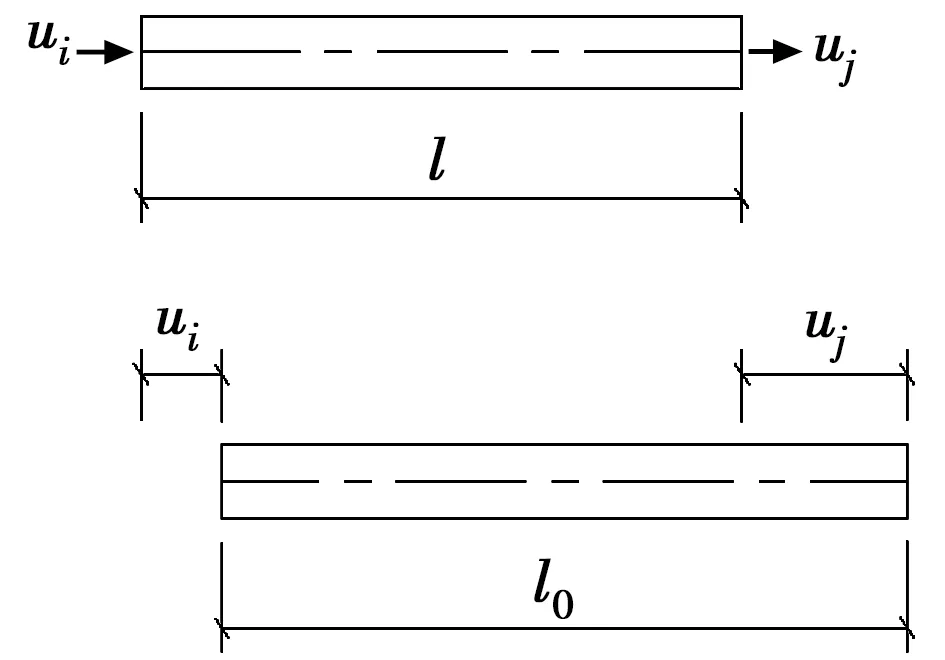
图5 单元产生轴向位移Fig.5 Axial displacement occurring in the
上述分析表明,平面梁单元预制构形与单元无应力状态量之间相互对应,预制构形的改变将引起单元无应力状态量的变化,反之亦然。
1.3 节段预制构形的确定
当单元预制构形参数确定后,可用以指导预制梁段的制作。图6所示为梁段预制构形尺寸,设构形顶、底边长度分别为ls、lx,构形截面形心距顶、底边的垂直距离分别为hs、hx,其余符号同前。由几何关系可得
(12)
由式(12)可得到预制构形的制作尺寸。
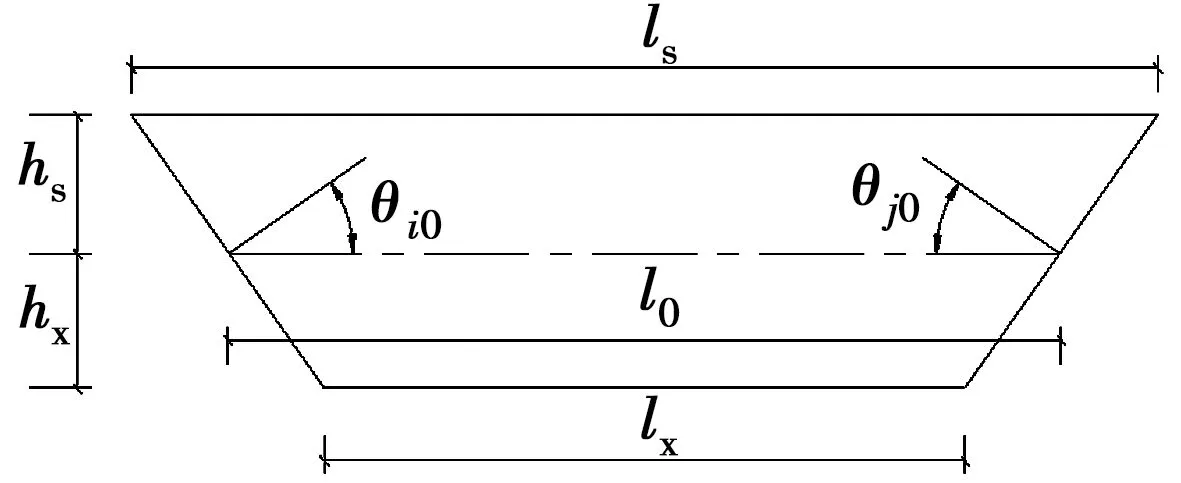
图6 梁段预制构形尺寸Fig.6 Precast configuration size of the beam
2 算例
以图7所示悬臂梁为例,对建立的单元无应力状态量与预制构形间关系式进行验证。图中悬臂梁跨径为30 m,梁的竖向弯曲刚度为4×107kN·m,梁上按3 m水平间距作用有10个60 kN的竖向集中荷载,要求荷载作用下主梁最终目标线形为抛物线y=x2/(2×104)。将主梁等距划分为10个单元,将主梁目标线形节点坐标和转角作为输入,由文献[16]推导的线形控制方程计算单元无应力状态量。对于预制节段施工主梁,结构线形通常以标高(坐标)进行控制,即施工过程中和最终线形要达到预定的标高值。不同的节点输入将计算得到不同的单元无应力状态量,进而对应不同的单元预制构形,为说明不同预制构形对主梁目标线形实现无本质影响,以考虑节点转角和不考虑节点转角两种线形(分别记为线形Ⅰ、线形Ⅱ,如图7(b)、(c)所示)作为输入。
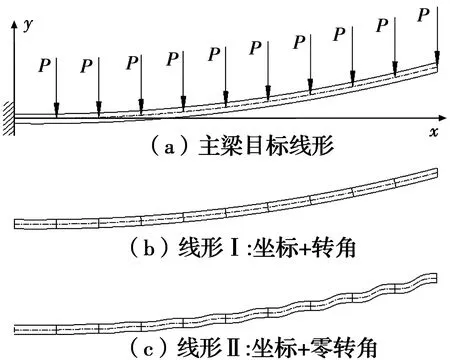
图7 主梁线形
2.1 线形Ⅰ计算结果
通过线形控制方程计算线形Ⅰ对应的梁段单元无应力状态量,由式(9)计算单元构形夹角,如表1所示。
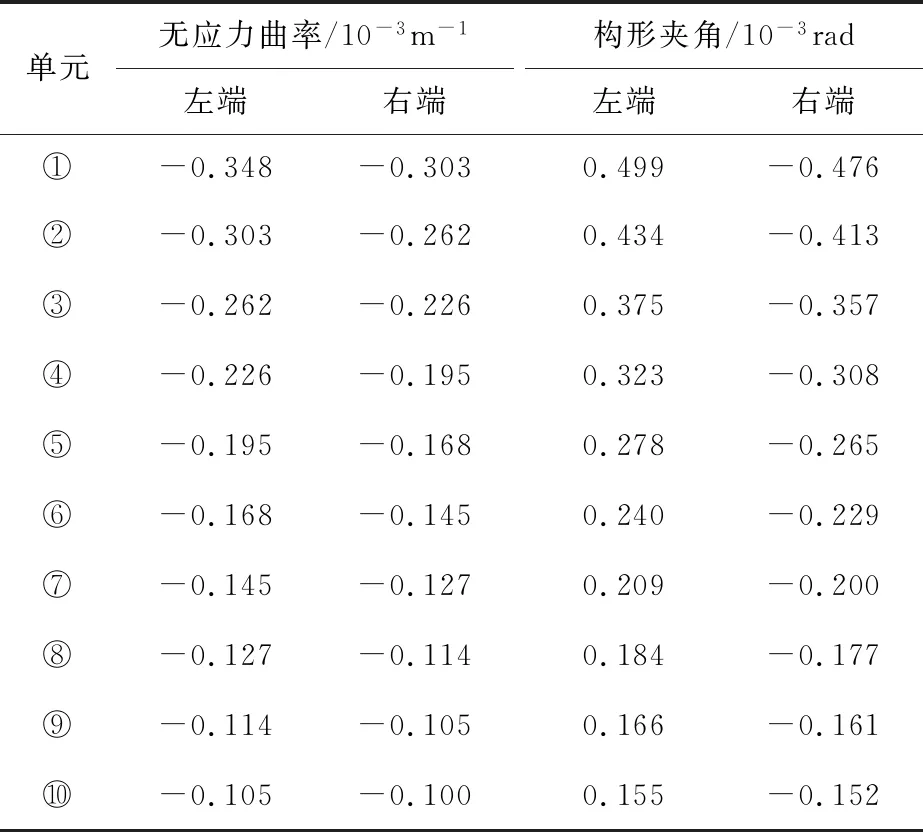
表1 线形Ⅰ无应力曲率及构形夹角Table 1 Unstressed curvature and configuration intersection angle of the alignment Ⅰ
主梁通过节段拼接形成,各预制节段间相对几何关系是确定的[16]。如图8所示,设第k-1(k=2,3,…,10)节段轴线与水平线间的夹角为αk-1,则第k梁段轴线与水平线间的夹角为
αk=αk-1-θj0k-1+θi0k
(13)
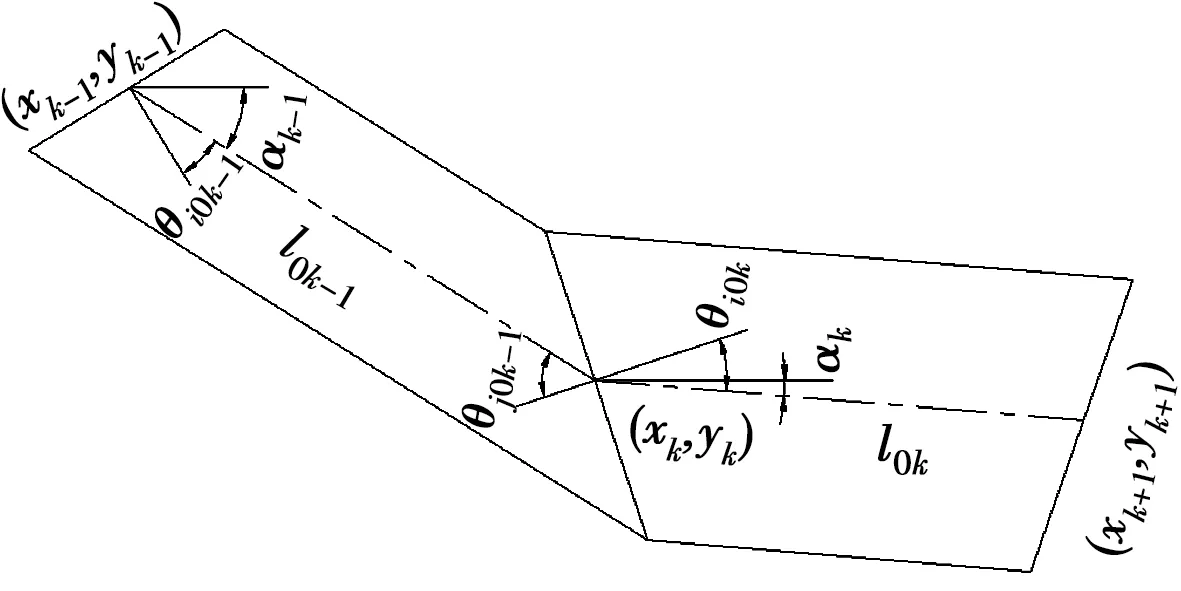
图8 预制构形间几何关系Fig.8 Geometrical relationship among the
设第k-1梁段始端坐标为(xk-1,yk-1),则得第k梁段始端坐标为
(14)
由式(13)、式(14)对主梁结构进行数值拼装,得到结构预拼线形,并将结构由于荷载P产生的位移叠加至预拼线形得到结构最终成桥线形,如表2所示。由表2可知,结构最终成桥线形与目标线形一致。
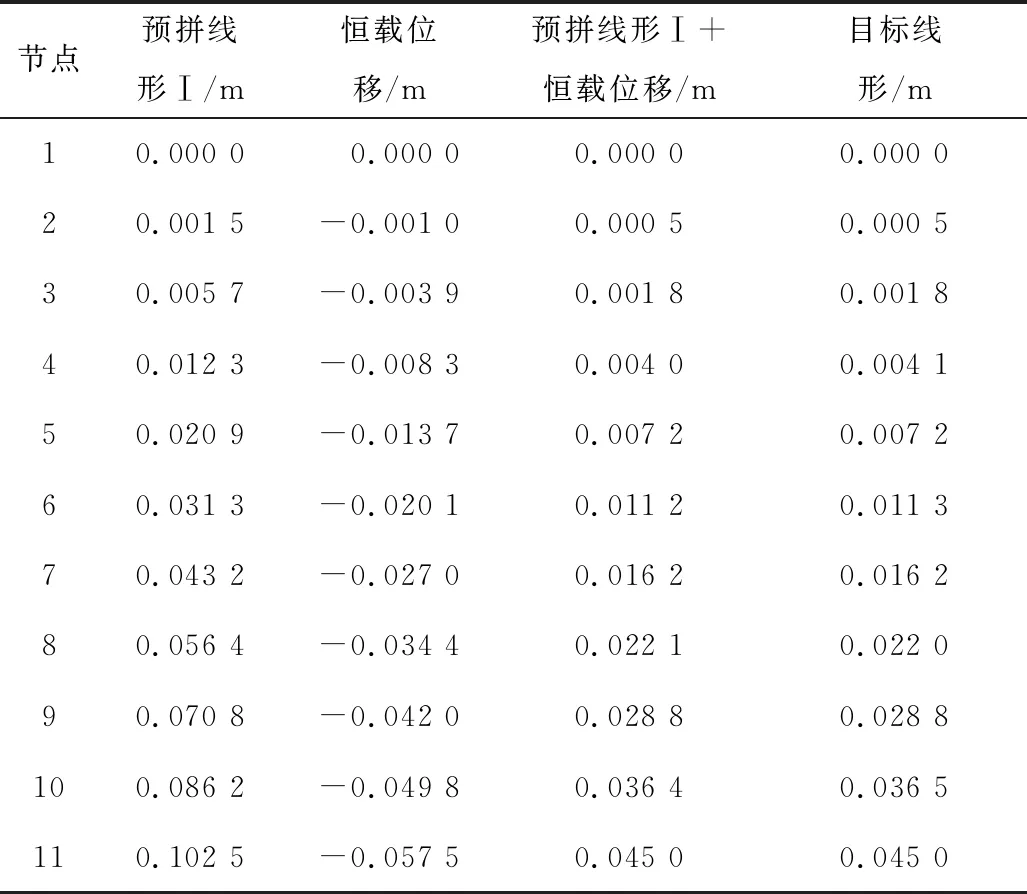
表2 线形Ⅰ拼装验证Table 2 Calculated assembly verification of the alignment Ⅰ
2.2 线形Ⅱ计算结果
通过线形控制方程计算得到线形Ⅱ对应的梁段单元无应力状态量,并由式(9)得单元预制构形夹角,如表3所示。
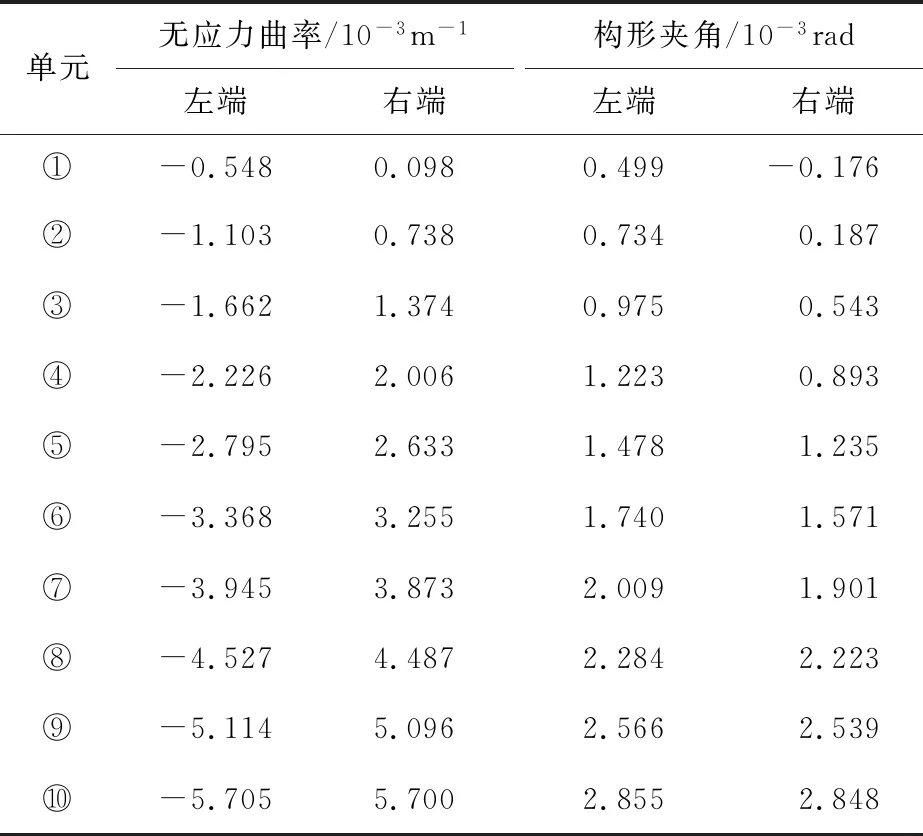
表3 线形Ⅱ无应力曲率及构形夹角Table 3 Unstressed curvature and configuration intersection angle of the alignment Ⅱ
由式(13)、式(14)对主梁结构进行数值拼装,得到结构预拼线形,并将结构由于荷载P产生的位移叠加至预拼线形得到结构最终成桥线形,如表4所示。由表4可知,结构最终成桥线形与目标线形一致。
2.3 线形Ⅰ与线形Ⅱ结果对比
1)对比表1与表3,线形Ⅰ与线形Ⅱ求得的单元无应力曲率和预制构形均不相同。

表4 线形Ⅱ拼装验证Table 4 Calculated assembly verification of the alignment Ⅱ
2)对比表2与表4,预拼线形Ⅰ与预拼线形Ⅱ一致,最终成桥线形Ⅰ与最终成桥线形Ⅱ节点坐标相等,且都与目标线形节点坐标一致,说明建立的无应力状态量与预制构形间的关系正确。
3)线形Ⅰ对目标线形上每个点的线形均满足要求,线形Ⅱ仅在节点上满足目标线形坐标要求,在节点间与目标线形不同。由于工程中常将节点间梁段简化为直线梁段,只要保证节点上线形满足要求即可,所以两种形式均可以满足工程要求。
3 结论
建立了平面梁单元无应力状态量与单元预制构形间的数学关系,并以悬臂梁为例对关系式进行验证,结果表明:
1)单元无应力状态量与单元预制构形间相互对应,不同的单元无应力状态量对应不同的单元预制构形;反之,不同的单元预制构形对应不同的单元无应力状态量。
2)数值计算结果表明,两种输入线形计算得到的最终成桥线形与目标线形一致,说明建立的平面梁单元无应力状态量与单元预制构形参数间的关系正确。
3)两种输入线形得到的单元预制构形不相同,但二者均能实现对主梁节点标高的控制,表明预制构形的差异对主梁标高控制无本质影响。对实际工程而言,只要确保节点标高满足目标线形标高控制要求,梁段的预制构形可不同。
4)梁段预制构形确定的一般步骤为:由线形控制方程计算目标线形对应的单元无应力状态量,再根据单元无应力状态量与无应力构形间的关系计算节段预制构形夹角及轴线长度,进而得到预制构形制造参数。

