海洋潮汐浪溅区混凝土表面氯离子浓度的改进计算模型

蔡荣，杨绿峰，余波

(1.广西财经学院 建设处，南宁 530008；2.广西大学 土木建筑工程学院；工程防灾与结构安全教育部重点实验室；广西防灾减灾与工程安全重点实验室，南宁 530004)

海洋潮汐浪溅区是海洋混凝土结构耐久性劣化最为突出的区域，因此，有必要建立该区域混凝土表面氯离子浓度Cs,ts的计算模型，为混凝土结构的耐久性分析和设计提供量化边界条件。目前，学者们建立了多种表面氯离子浓度计算模型。其中，Marques等[1]建立了Cs,ts与水胶比之间的线性关系模型；文献[2]建立了考虑水胶比和胶凝材料种类影响的关系模型。上述模型只考虑了材料特性的影响，而忽略了暴露时间t的影响。由于水泥水化程度的发展，混凝土越来越密实，导致Cs,ts具有显著的时变特性。对此，文献[3-8]分别利用对数型、幂函数型、指数型等函数来描述了Cs,ts的时变规律，但无法合理描述初期增长较快、后期趋于稳定的时变规律。文献[9-11]建立了Cs,ts与水胶比和暴露时间之间的关系模型，但忽略了胶凝材料种类对表面氯离子浓度的影响。由此可见，Cs,ts不仅与水胶比和胶凝材料种类等材料参数密切相关，而且具有显著的时变特性，因此，有必要综合考虑水胶比、胶凝材料种类和暴露时间的影响，建立Cs,ts的多因素模型。蔡荣等[12]初步建立了Cs,ts与水胶比、胶凝材料种类和暴露时间之间的关系模型，但直接采用了DuraCrete模型[2]的胶凝材料种类修正系数，无法合理描述不同胶凝材料对Cs,ts的影响规律。

鉴于此，本文基于304组海洋潮汐溅区现场自然暴露混凝土的试验数据，分析了水胶比、胶凝材料种类和暴露时间对Cs,ts的影响规律，进而结合二阶段多元非线性回归分析，分别确定了硅酸盐水泥(OPC)、粉煤灰(FA)、矿渣(SG)和硅灰(SF)等胶凝材料种类对Cs,ts的修正系数，建立了Cs,ts的改进模型，并利用试验数据和现有模型对比，验证了模型的适用性。

1 表面氯离子浓度的主要影响因素分析

1.1 潮汐浪溅区自然暴露混凝土的试验数据

为了研究海洋潮汐浪溅区混凝土表面氯离子浓度Cs,ts的主要影响因素及其影响规律，从文献[10，13-20]中搜集了304组现场自然暴露混凝土的试验数据。其中，文献[10，13-19]直接提供了297组依据Fick第二定律一维解析解拟合确定的表面氯离子浓度数据，文献[20]仅提供了混凝土内部氯离子的浓度分布数据，本文依据Fick第二定律的一维解析解[13,16]通过逆向拟合[21]分析得到对应的表面氯离子浓度数据，并据此建立了Cs,ts的试验数据库，基本信息见表1。

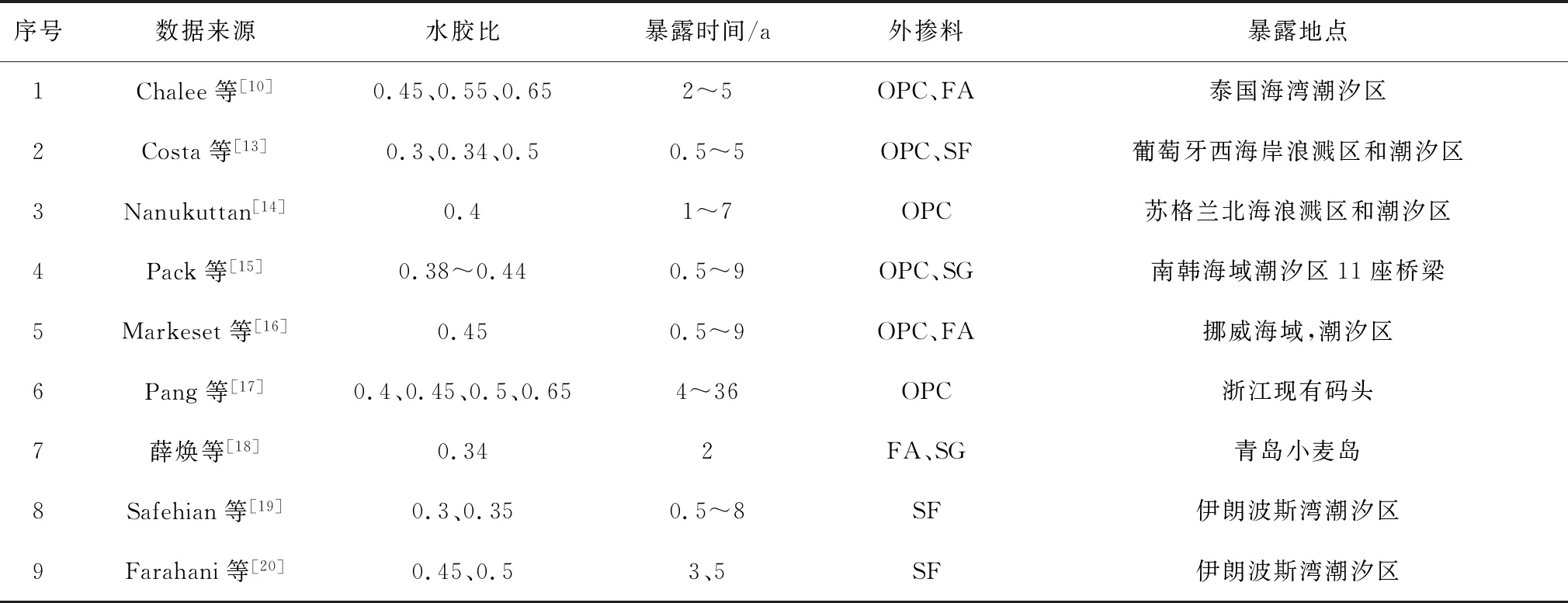
表1 试验数据的信息Table 1 Information of experimental data

1.2 材料参数的影响

在海洋潮汐浪溅区，混凝土表层对流区的氯离子传输主要受毛细吸附、干湿循环等作用的影响，而混凝土内部的氯离子传输主要受扩散作用控制，通常可以利用Fick第二定律来描述。由于水胶比(RW/B)和胶凝材料种类对混凝土的孔隙率和水化过程具有重要影响[22]，进而会影响混凝土中氯离子的扩散和积聚规律，所以RW/B和胶凝材料种类是影响混凝土表面氯离子浓度(Cs)的重要材料参数。

在RW/B的影响方面，王胜年等[23-24]通过现场暴露试验数据分析发现，RW/B与Cs之间近似呈线性关系；另外，文献[1-2，9]均认为Cs随着RW/B呈线性增大趋势。基于表1中的试验数据，可以分析RW/B对海洋潮汐浪溅区混凝土表面氯离子浓度(Cs,ts)的影响规律，如图1所示。由图1可知，Cs,ts与RW/B近似呈线性关系。

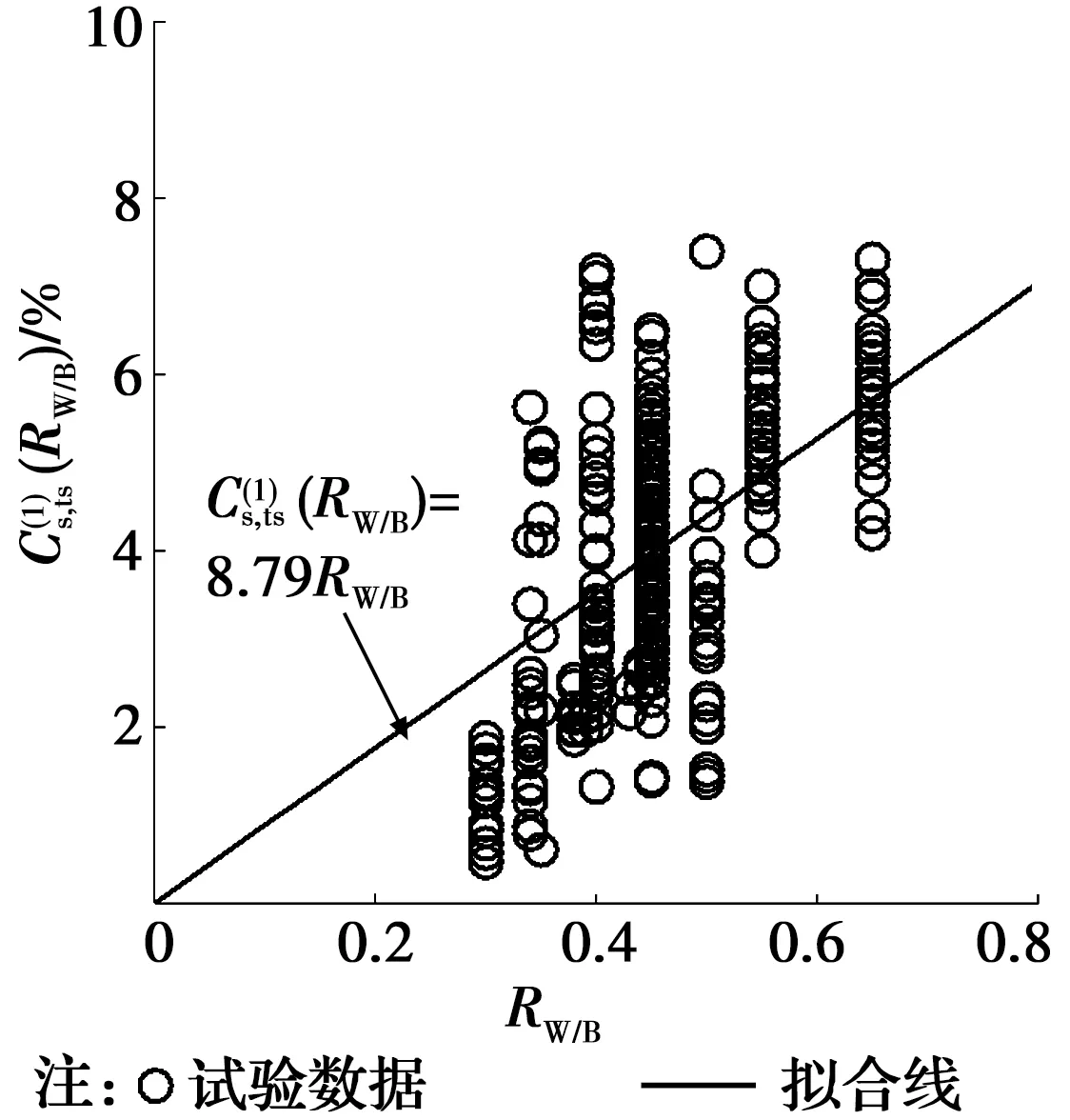
图1 水胶比对Cs,ts的影响Fig.1 Influence of water-to-binder ratio on

混凝土组分中，水泥是最基本的胶凝材料。此外，粉煤灰、硅灰、矿渣粉等矿物掺合料都是常见的胶凝材料。由于水化作用，矿物掺合料会降低混凝土的孔隙率并阻断孔隙的连通性，从而影响混凝土中氯离子的传输和积聚规律，进而对Cs产生重要影响。然而，由于不同矿物掺合料的水化机理和过程不尽相同，所以，不同胶凝材料种类对Cs的影响变化规律也不同。研究表明[16,25]，掺加FA会增加Cs，其原因在于，粉煤灰颗粒为空心结构，且比表面积较大，因而具有物理吸附氯离子的能力；同时，FA中含有大量的氧化铝，与氢氧化钙发生二次水化反应会生成水化铝酸钙，对氯离子具有较强的固化能力；此外，掺加FA会增强混凝土对水的吸附能力，而水溶液是传输氯离子的重要媒介。此外，与FA相比，SG和SF的微集料效应和火山灰效应更加显著，从而会改善混凝土的抗氯离子渗透性能，进而降低Cs[26-28]。参考DuraCrete[2]模型，通过引入修正系数Ac来考虑胶凝材料种类的影响，将材料参数与Cs，ts之间的关系描述为

(1)

1.3 暴露时间的影响

由于水泥水化程度会随着暴露时间(t)的增加不断完善，导致混凝土逐渐趋于密实[29]，所以，Cs在暴露初期增长较快，随着t的增加逐渐趋于稳定，时变特性显著。学者们通常利用对数型[3-4,10]、幂函数型[5,16]和指数型[6-8,25]等函数形式来描述Cs的时变特性。其中，随着t的增加，对数型和幂函数型模型的预测值趋于稳定的规律不明显，而指数型模型更加符合Cs的时变规律。利用表1的试验数据，可以分析Cs,ts的时变规律，如图2所示。图中，R2是可决系数，可以看出，4条曲线的可决系数都大于0.8，说明利用指数型模型可以较好地描述Cs,ts的时变特性，所以，Cs,ts与t之间的关系可以表示为

(2)

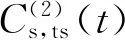
图2 暴露时间对Cs,ts的影响Fig.2 Influence of exposure time on

2 表面氯离子浓度的多因素模型

2.1 多因素模型的建立

根据上述Cs,ts的主要影响因素分析可知，Cs,ts是关于RW/B和t的二元函数，且需要考虑胶凝材料种类的影响。为了定量分析RW/B与t之间的相关性，根据表1中304组现场自然暴露混凝土的试验数据，利用式(3)计算RW/B与t之间的相关系数ρ。

0.06

(3)

式中：ρ为暴露时间t和水胶比RW/B之间的相关系数；N为试验数据的数量，这里为304；xi和yi分别为第i组现场自然暴露试验数据中t和RW/B的取值。

根据式(3)的计算结果可知，暴露时间t和水胶比RW/B之间的相关系数ρ=0.06，说明t和RW/B两个因素之间的相关性很小，可以近似认为两者不相关。鉴于此，在式(1)和式(2)所建立的单因素模型基础上，可以将Cs,ts的多因素模型描述为

Cs,ts(RW/B,t)=αts·Ac·RW/B·(1-e-βts·t)

(4)

式中：αts和βts表示待定拟合系数。

2.2 模型参数的确定

基于表1中304组Cs,ts的试验数据，结合高斯-牛顿迭代法[30]和两阶段多元非线性回归分析方法[21]来待定参数αts、βts和Ac。首先，令Ac=1，通过多元非线性回归分析，可以确定αts和βts分别为10.01和0.96，将αts和βts的拟合值代入式(4)，可获得考虑RW/B、胶凝材料种类和t影响的Cs,ts改进模型。

Cs,ts=10.01Ac·RW/B·(1-e-0.96t)

(5)

在式(5)的基础上，利用表1中不同种类胶凝材料(OPC、FA、SG和SF)的试验数据，通过回归分析，可以确定不同胶凝材料种类的修正系数Ac，并与DuraCrete模型[2]中的材料修正系数Ac取值进行对比分析，见表2。

表2 Ac取值的对比分析Table 2 Comparison of values of Ac

由表2可知，本文模型和DuraCrete模型的胶凝材料修正系数Ac取值规律不同。从1.2节的影响机理分析可知，掺加FA会增加Cs,ts，因而FA混凝土的Ac高于OPC混凝土的Ac；与此相反，掺加SG和SF能够显著降低Cs,ts，因而SG混凝土和SF混凝土的Ac低于OPC混凝土的Ac。本文模型的Ac取值符合上述规律，能够正确反映胶凝材料种类对Cs,ts的影响规律。而DruaCrete模型中SF混凝土的Ac值高于OPC混凝土的Ac，FA混凝土的Ac值低于OPC混凝土的Ac，与前述试验结果不符，由此说明，DruaCrete模型的Ac取值不能正确反映胶凝材料种类对Cs,ts的影响规律。

将表2中本文模型的Ac值代入式(5)，可以建立同时考虑暴露龄期、水胶比和胶凝材料种类影响的海洋潮汐浪溅区混凝土表面氯离子浓度Cs,ts的多因素模型。

3 对比分析与验证

为了验证所建立Cs,ts模型的有效性和适用性，选用现有的9种计算模型进行对比分析，见表3。需要说明的是，为了与试验数据进行对比分析，各模型的分项系数统一取为1.0。

表3 不同计算模型的表达式Table 3 Expressions for different computational models

3.1 模型预测效果对比分析

利用文献[13,16]提供的现场暴露混凝土的试验数据，检验分析不同模型的合理性，如图3所示。由图3可知，Cs,ts在前5 a内增长较快，后期逐渐趋于稳定，特别是在图3(b)、(c)中更为明显。DuraCrete模型低估了3 a以后的试验值；JTS 153模型高估了前5 a内的试验值；当暴露时间较短(如5 a内)时，文献[10]模型(对数型)和文献[11]模型(平方根型)的预测值与试验值吻合较好，但是当暴露时间较长(如5 a后)时，则会出现明显高估，且文献[10]模型的初值出现负值，不符合工程的物理意义；由图3(a)、(b)可以看出，当暴露时间较长时，文献[12]模型的预测值明显高于实测值。文献[13]模型和文献[3]模型(对数型)的预测值在暴露初期显著低估，而当暴露时间较长时，文献[13]模型和文献[3]模型(对数型)出现高估。总体而言，本文模型的预测值与试验值吻合较好，前5 a快速增长，随后逐渐趋于稳定，符合工程规律。

3.2 模型预测精度对比分析

基于表1中304组Cs,ts的试验数据，将本文模型和表3中的9种模型进行对比分析，以验证各模型的计算精度，如图4所示。其中，文献[33]模型的参数根据文献[12]取值。为了定量对比分析各模型的预测精度，分别定义残差均方差δ、模型预测值与实测值比值的均值μ。

(6)

由图4可以看出，文献[10]模型、文献[11]模型、JTS 153模型(潮汐区)、JTS 153模型(浪溅区)和文献[33]模型的散点大都在等值线上方，明显偏大；而DuraCrete模型、文献[3]模型、文献[13]模型和LNEC模型的散点偏离30%上下界较多，说明这4个模型预测结果离散性大。同时，可以看到，上述9个模型的δ值都在1.46%以上，从概率统计的角度再次验证了上述模型预测值与试验值相比离散性较大，模型拟合效果较差。文献[12]模型和本文模型的散点相对集中分布在等值线附近，特别是本文模型的δ值最小，而且与文献[12]相比，本文模型的μ值更接近于1.0，说明本文模型具有更高的预测精度，且离散较小。

造成各模型拟合效果不同的原因在于，DuraCrete模型、文献[10]模型、文献[11]模型、文献[13]模型、文献[3]模型、LNEC模型和文献[33]模型都没有综合考虑暴露时间、水胶比和胶凝材料种类的影响，只是考虑了3个主要因素中的1～2个，导致预测精度低，且预测结果离散性大。而本文建立的多因素模型综合考虑了水胶比、胶凝材料种类、暴露时间的影响，能够合理反映自然暴露环境下混凝土表面氯离子浓度的变化规律，因而预测结果精度较高，且离散性较小。文献[12]模型尽管综合考虑了3类主要因素的影响，但该模型的胶凝材料种类修正系数与DuraCrete模型相同，依据为数不多的试验数据并利用常规拟合分析方法确定，缺乏针对性，难以合理反映胶凝材料种类的影响规律。而本文模型有针对性地采用二阶段回归方法分析确定胶凝材料种类修正系数，更加合理。特别需要说明的是，本文模型与其他模型相比，所依据的304组现场自然暴露试验数据来源地更加广泛，且样本总量远大于其他模型，从而保证了本文模型参数的拟合结果具有更高的稳定性和更广泛的适用性。

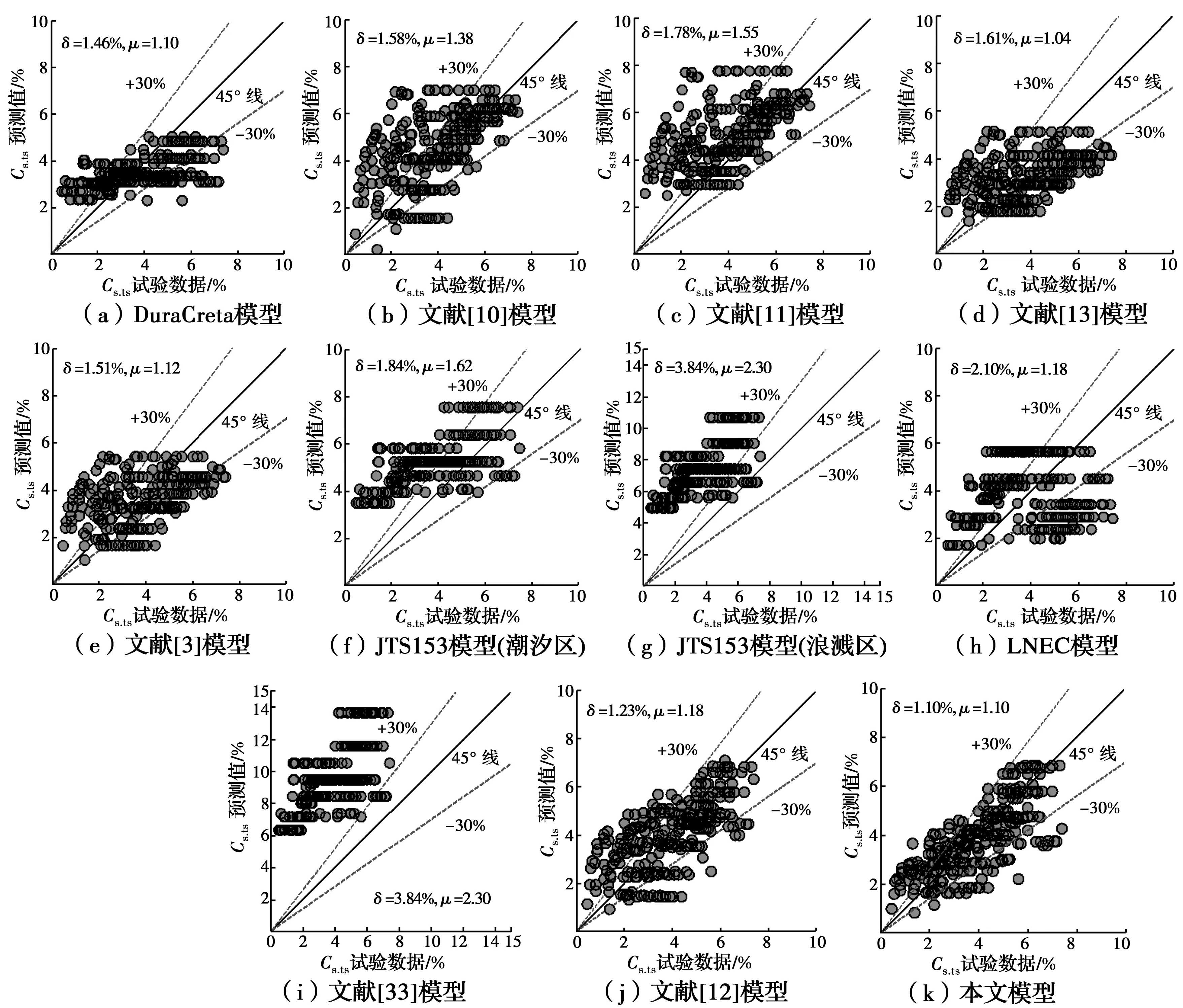
图4 基于试验数据的模型预测值对比Fig.4 Comparison of predicted results of different models based on experimental

4 结论

收集遴选了304组海洋潮汐溅区现场自然暴露混凝土的试验数据，利用二阶段多元非线性回归分析方法建立了混凝土表面氯离子浓度Cs,ts的改进模型。分析表明：

1)Cs,ts与水胶比之间呈线性增大关系，且胶凝材料种类对Cs,ts的影响显著；Cs,ts在暴露初期快速增长，随后逐渐趋于稳定，可以利用指数型函数来描述其时变规律。

2)本文Cs,ts模型综合考虑了暴露时间、水胶比和胶凝材料种类的影响，且利用二阶段多元非线性回归分析确定了胶凝材料种类修正系数，通过与现有模型和试验数据的对比分析，验证了本文的Cs,ts模型具有较好的适用性。

3)本文Cs,ts模型所依据的304组现场自然暴露混凝土的试验数据来源地更加广泛，且样本总量远大于其他模型，从而保证了本文Cs,ts模型参数的拟合结果具有更高的稳定性和更广泛的适用性。