基于增量动力分析法的高层建筑-阻尼器系统地震易损性分析

国巍，曾晨，潘毅，赖炜煌，胡思远

(1.中南大学 a.土木工程学院；b.高速铁路建造技术国家工程实验室，长沙 410075；2.西南交通大学 土木工程学院，成都 100191；3.同济大学 土木工程学院，上海 200092)

大部分震级较小的远场地震动给结构带来的工程损害并不严重，但在震级较大时，远场地震动中的短周期成分将会迅速衰减，长周期成分被场地软土层放大，使得地震动的周期更加接近地表上高层建筑的自振周期，结构产生较大的动力响应。通常可在建筑结构中设置阻尼器进行消能减震，应用在结构中的典型阻尼器包括摩擦阻尼器、粘滞阻尼器和防屈曲支撑。目前，中国《建筑抗震设计规范》(GB 50011—2010)对于消能减震设计已有相关规定，速度相关型阻尼器以及位移相关型阻尼器是其中重点研究的技术。

摩擦阻尼器具有耗能能力强、摩擦机构简单、取材容易、造价低廉、荷载及频谱特征对其性能影响较小的特点[1]。粘滞阻尼器利用平板或活塞在具有高度粘性的液体中运动耗能的原理实现消能减震[2-3]。防屈曲支撑具有稳定的滞回性能和耗能能力，设置在建筑主体结构中以形成减震体系[4-6]。增量动力分析方法(Incremental Dynamic Analysis, IDA)是结构抗倒塌分析的主要方法，学者们利用该方法研究发现，与传统抗弯框架和设置防屈曲支撑的结构相比，设置粘滞阻尼器能提供更好的抗倒塌性能[7]，并评估了将金属摩擦阻尼器应用于钢筋混凝土结构中结构在地震下达到各个损伤状态的概率[8]。

目前，基于规范设计的建筑-阻尼器系统在强地震下的实际响应是否与设计结果存在偏差、在同一设防目标下不同类型阻尼器的性能是否存在差异尚不清楚。笔者基于规范建立了20层钢框架Benchmark模型，并考虑设置3种典型阻尼器——摩擦阻尼器、粘滞阻尼器和防屈曲支撑，选取远场强地震动进行IDA分析，研究结构在设置不同阻尼器时的地震易损性，对比分析不同阻尼器的性能，研究了远场地震动对高层建筑结构抗震性能的影响。

1 基于规范设计的Benchmark模型

美国土木工程师学会(ASCE)提出了基于美国规范建立的Benchmark模型[9]，使学者能够基于一致的结构模型进行振动控制方法及新型减隔震装置研究。中美两国现行抗震设计规范存在较大差异，对于地震区划的划分、场地类别的划分、地震作用参数取值以及地震作用计算准则的处理方式不同，需要一定程度的统一后才能进行地震作用的比较和分析[10]。两国规范在钢材以及混凝土的品种、强度取值不同，不能简单类比[11]，两国规范的设计反应谱具有相同的基本特征，但在反应谱最大值、周期范围等方面存在差异[12]，中国规范在考虑地震作用的荷载组合、刚度限值、剪重比限值等方面要比美国规范更加严格[13]。由于两国规范的差异，不能简单地对现有Benchmark模型进行消能减震设计，为了能够在中国现行抗震规范下进行高层建筑中典型阻尼器性能的评估分析，需要建立基于中国规范设计的Benchmark模型。

1.1 工程概述

选择一座20层钢框架结构，所在地为陕西省宝鸡市，抗震设防烈度为7度，地震分组为第2组，场地类型为二类场地，设计地震基本加速度为0.15g，钢结构抗震等级为3级[14]。先用PKPM软件进行该结构的设计和布置，结果见图1(a)。

主体结构为钢框架结构，平面长宽为39.6 m×33 m，长宽比为1.2，符合长宽比不超过4的限值。底层高度为4.2 m，其余各层均为3.3 m，总高度为66.9 m，最大高宽比为2.07，小于高宽比不超过6.5的限值。结构设计遵循对称的思路，有效地减少扭转和平动相互之间的耦联，使周期比得到一定降低。建筑平面纵向共6榀，每一榀6跨，横向共7榀，每一榀5跨。

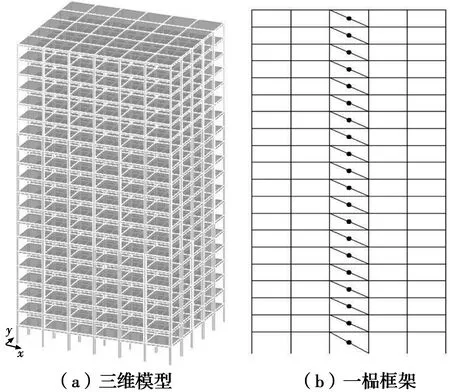
图1 钢框架结构示意图Fig.1 Schematic of the steel frame

1.2 结构基本信息

所有梁柱构件都采用Q345钢。主梁采用窄翼缘H型钢，柱采用方型钢，各层梁、柱的尺寸详见表1。各楼层的楼板采用现浇混凝土楼板，厚度统一取为120 mm，并定义了5个标准层，分别为底层、2～7层、8～14层、15～19层以及顶层，各楼层楼板采用刚性楼板假定。根据自行设计的梁柱布置情况，在各标准层布设梁柱构件。

表1 各楼层主要构件规格
Table 1 Specifications for each floor mm

楼层主梁柱第1层HN500×200×10×16□650×650×30×30第2～7层HN500×200×10×16□600×600×20×20第8～14层HN400×200×8×13□500×500×15×15第15～20层HN400×200×8×13□400×400×15×15

1.3 荷载标准值的确定

楼面恒载的确定：假设每一层的楼面恒载均一致，参考汉森写字楼框架结构的设计标准[15]：10 mm厚混合砂浆抹灰取0.17 kN/m2，20 mm厚水泥砂浆找平取0.40 kN/m2，120 mm厚现浇混凝土楼板取3 kN/m2，某耐磨型的地板砖取1 kN/m2，吊顶取0.4 kN/m2，合计为4.97 kN/m2。

楼面活载的确定：对于民用建筑的楼面均布活载规定的取值[16]，选用写字楼的活载标准值为2.0 kN/m2。

梁间线荷载的确定：梁间线荷载包括内外隔墙和女儿墙的自重。内墙：两侧20 mm厚混合砂浆抹灰，300 mm厚蒸压粉煤灰加气砼砌块，取7 kN/m；外墙：两侧20 mm厚混合砂浆抹灰，200 mm厚蒸压粉煤灰加气砼砌块，取5.5 kN/m；女儿墙：顶层最外侧梁承受女儿墙的线荷载，取标准值2.0 kN/m。

1.4 计算结果

根据PKPM的建模电算结果，可以得到结构各楼层的基本信息，见表2，为后续有限元建模提供了参数。

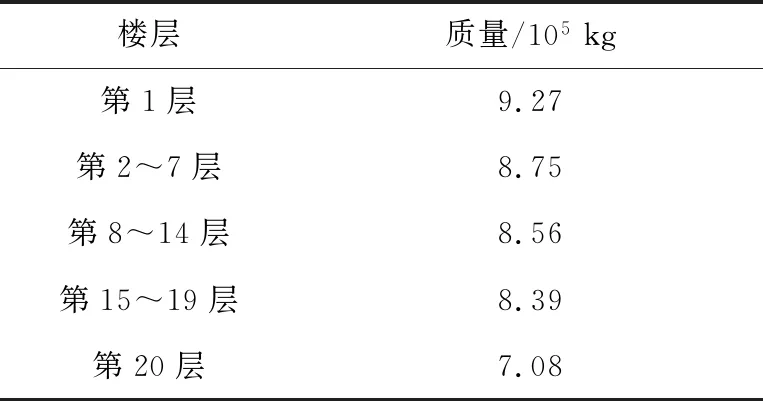
表2 楼层质量Table 2 Seismic mass

对钢框架结构在多遇地震下的抗震变形进行验算，高层钢框架的弹性层间位移角限值为1/250[14]。结果见表3。Y方向的刚度较低，Y方向的顶点位移和层间位移角较X方向大，两个方向的最大层间位移角均小于1/250的限值，且与限值相差不是太大，钢框架结构刚度合理。

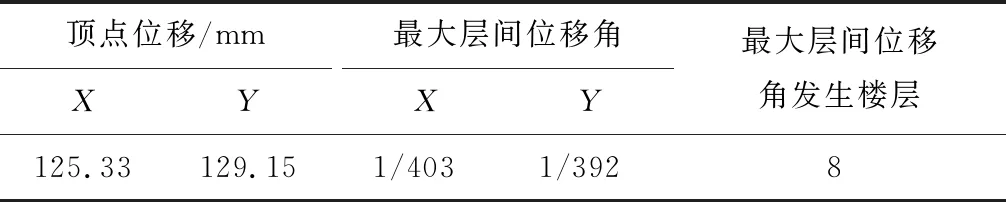
表3 水平地震力作用Table 3 Horizonal earthquake effect

最后，利用OpenSees取框架结构Y方向的一榀建模，如图1(b)所示，凝练Benchmark模型以进行地震易损性分析，根据模态分析结果，如表4所示，OpenSees中建立的结构模型与PKPM中建立的模型拟合度很高，体现了原结构的特点，可进行后续分析。

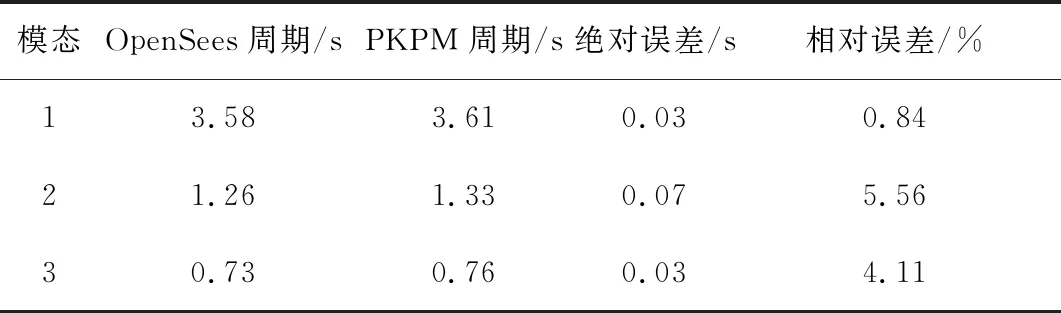
表4 模态分析对比Table 4 Comparison of modal analysis

2 阻尼器参数设计

2.1 结构减震设计目标

控制结构的位移响应是保证结构抗震性能的有效手段，即在一定水准的地震作用下，以预期的结构位移反应为设计目标，从而实现结构在地震作用下预期的性能要求。

首先确定消能减震的控制目标，即确定地震作用的降低程度，取楼层中发生层间位移角的最大值为无阻尼器结构对应响应的76%作为结构减震设计目标，并以此减震目标作为3类阻尼器共同的设计目标，在同一设计目标下评估3类阻尼器的减震性能。

2.2 阻尼器采用的模型

摩擦阻尼器、防屈曲支撑均采用Bouc-Wen模型，Bouc-Wen模型是经典的位移型阻尼器滞回曲线的恢复力模型，由于精准的拟合性，常被用于各类力学模型的研究[17]，其恢复力表达式为

F=αKΔu+(1-α)Kz

(1)

(2)

式中：F为阻尼力；α为屈服后阻尼器的刚度比；K为阻尼器的初始刚度；Δu为阻尼器的位移；z为与滞回曲线有关的形状函数；A、β、γ、n为确定滞回曲线形状的4类参数。

在进行摩擦阻尼器、防屈曲支撑设计时，采用拟合文献[18-19]中提供的摩擦阻尼器和防屈曲支撑的形状函数参数来对摩擦阻尼器和防屈曲支撑进行辅助设计，如图2所示。

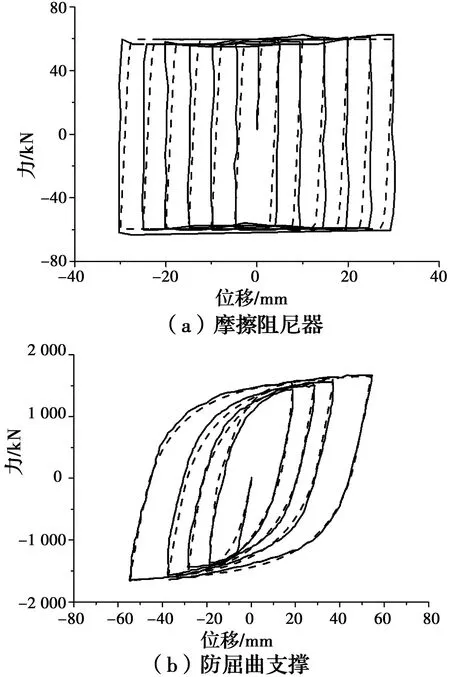
图2 阻尼器模型曲线与试验曲线的拟合Fig.2 The fitting of damper model and test

粘滞阻尼器采用线性模型，线性模型为阻尼单元的形式

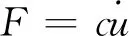
(3)

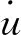
2.3 附加有效刚度和附加有效阻尼比的计算

1)附加有效刚度——等价线性化方法

Keff=Fmax/Δumax

(4)

式中：Keff为阻尼器附加到结构的有效刚度；Fmax为阻尼器所受的最大荷载；Δumax为阻尼器的最大位移。

2)附加有效阻尼比——能量化方法

(5)

式中：ξd为阻尼器附加给结构的有效阻尼比；Wcj为在预计的层间位移下第j个阻尼器进行一周期往复循环运动的耗能量；Ws为水平地震作用下消能减震结构的总应变能[19]。

2.4 设置阻尼器的位置

阻尼器不同的布置方式也会对阻尼器的参数设计带来影响，阻尼器的布置宜沿结构主轴方向设置，并形成均匀合理的结构体系，采用每层简单斜撑布置的形式，每层均匀布置，如图1(b)所示。

2.5 阻尼器参数设计总体流程

根据已选定的阻尼器原型，确定相应滞回曲线的形状参数，之后再调整阻尼器的力学参数以满足设计要求，对附加阻尼比作出假设，并进行后续的结构变形计算，但此时计算得到结构的变形并非真实变形，需要再次采用式(5)求出阻尼器的附加阻尼比，将附加阻尼比的假定值与计算值进行比较，若二者相差很大，进行迭代计算，直到两次结果相近。阻尼器参数设计总体流程图如图3所示。

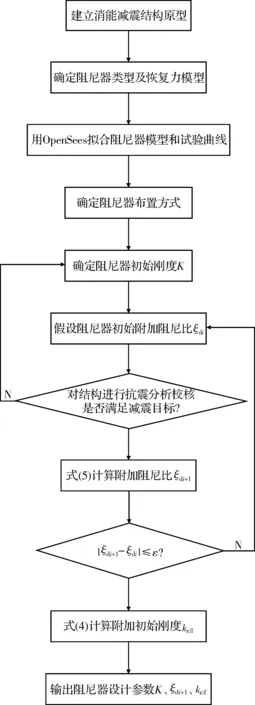
图3 阻尼器参数设计总体流程Fig.3 Damper parameter design flow

在这几类典型阻尼器中，除了粘滞阻尼器仅提供结构附加阻尼比之外，其他阻尼器均可以提供附加阻尼比和附加刚度。按照中国抗震设计规范的设计流程和方法，最终设计的阻尼器参数如表5和图4所示。

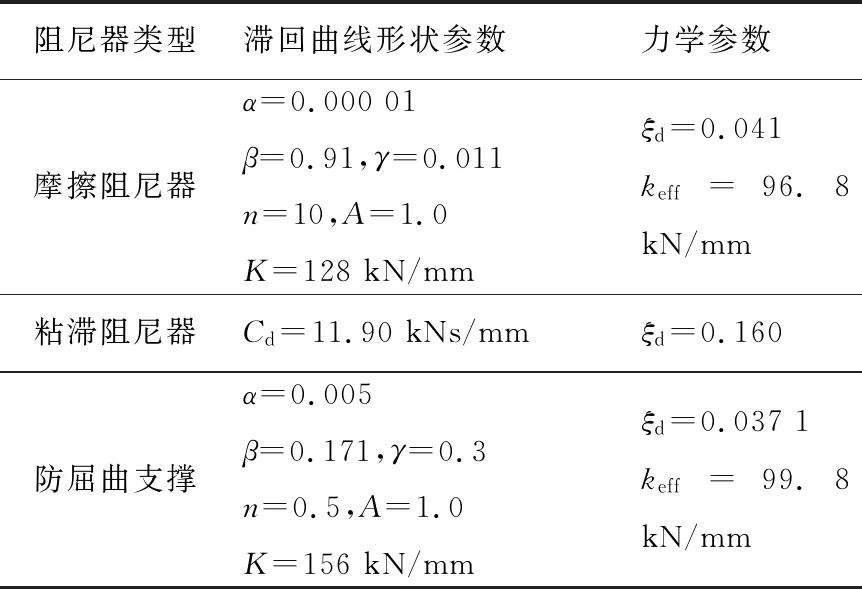
表5 各类阻尼器的设计参数Table 5 Design parameters of the dampers

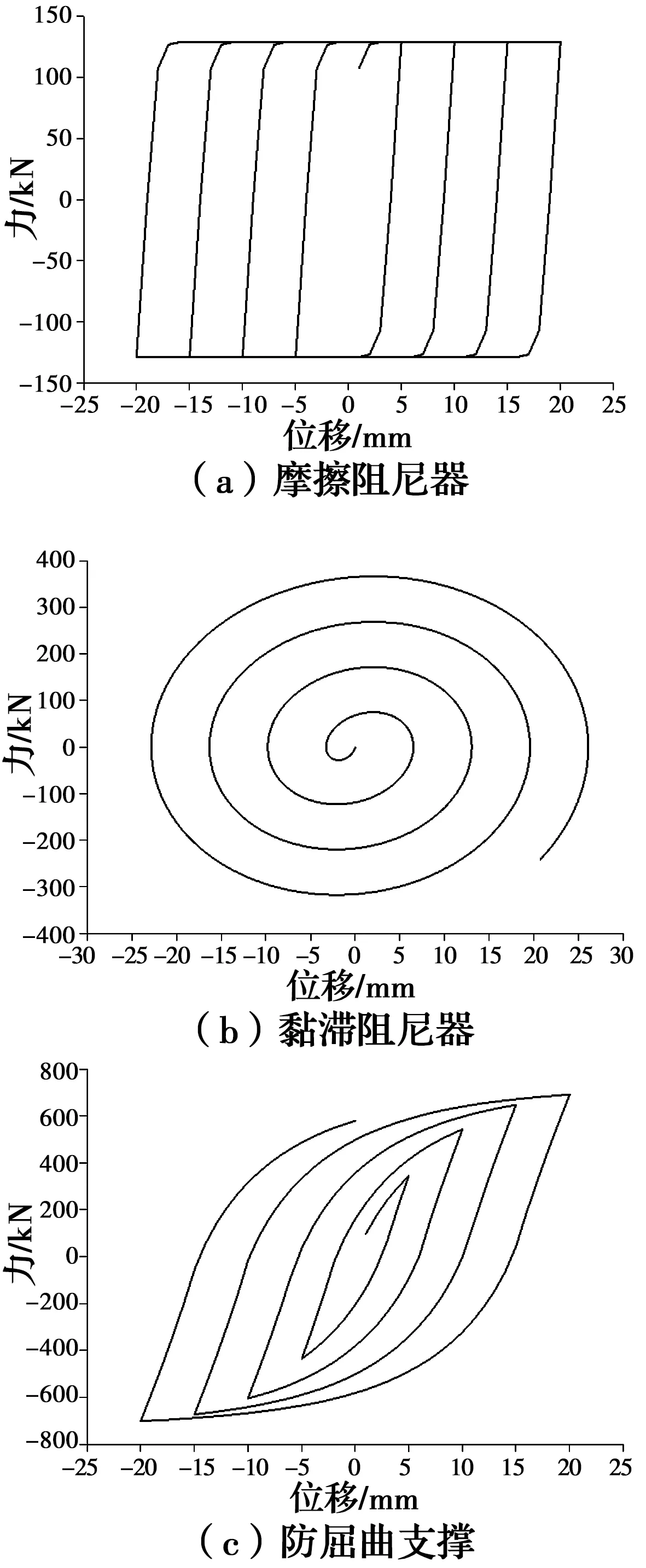
图4 阻尼器设计结果Fig.4 The design result of

3 IDA分析基本过程

IDA分析是将地震动的强度赋予单调递增的比例系数，得到不同强度指标度量值IM(Intensity Measure)；对结构进行动力时程分析，得到的不同强度下结构损伤指标度量值DM(Damage Measure)，从而建立反映结构响应历程的以IM为纵坐标、DM为横坐标的曲线。在这一过程中，结构历经了线弹性阶段、弹塑性阶段以及破坏阶段的完整响应历程，可以全面体现地震下结构的动力响应过程。

3.1 地震动的选取

文献[20]定义：小于60 km的断层距地震动定义为近场地震动，60～200 km范围的断层距地震动定义为中场地震动，大于200 km的断层距地震动定义为远场地震动。

根据该20层钢框架结构的基本信息，地震影响系数最大值取0.12，特征周期取0.4 s，钢结构的阻尼比取0.02，根据《建筑抗震设计规范》[14]得到场地的设计反应谱见图5。

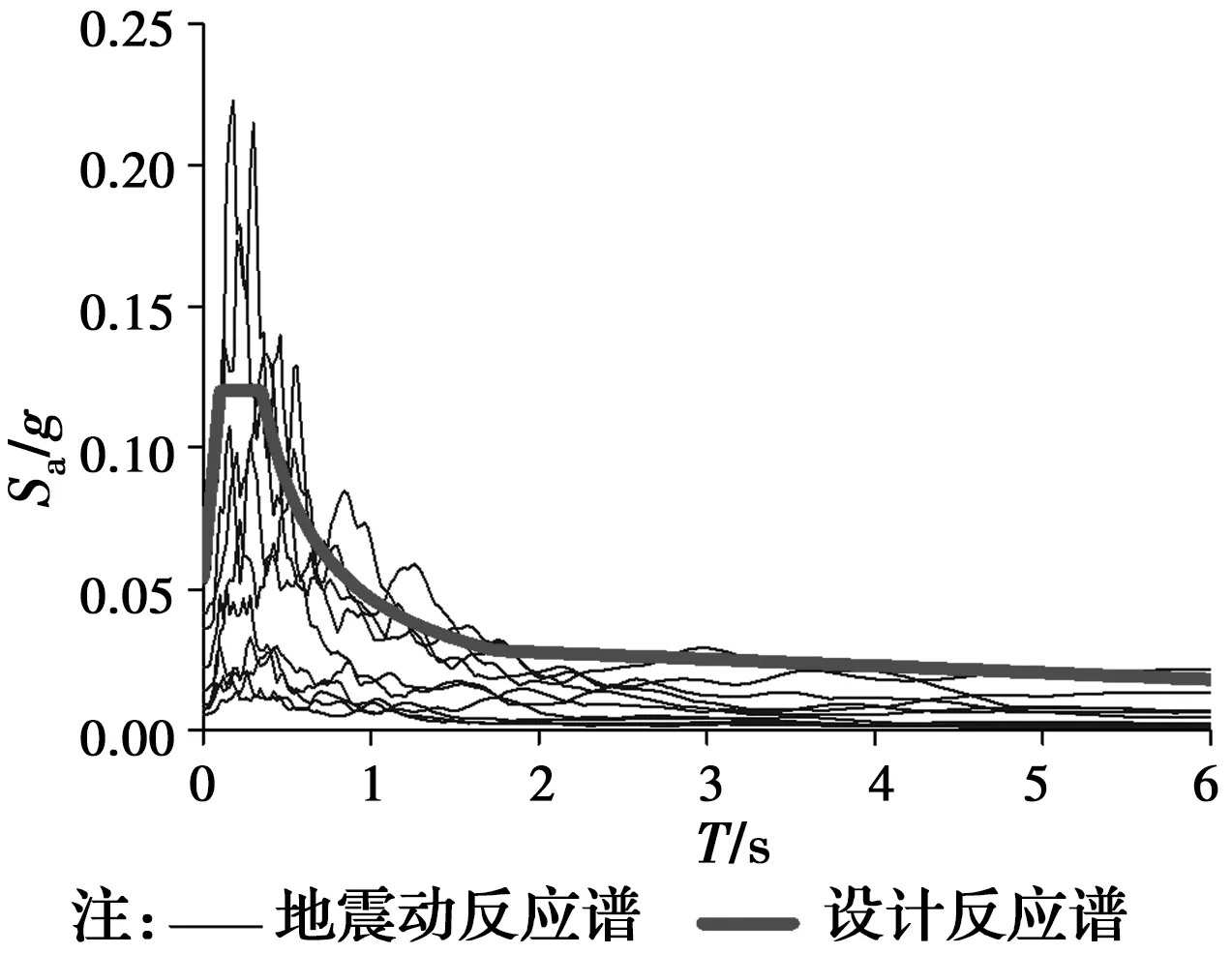
图5 地震动反应谱Fig.5 Response spectrum of ground

根据设计反应谱查找拟合度最高的地震动，相应的参数：矩震级为6.5～7.8级，震中距为200～500 km，符合远场地震动的定义，30 m深度土层的剪切波波速为150～500 m/s；强震持续时间为19～36 s，选择10条平行于断裂带方向的水平地震下地震动数据，其基本信息见表6。

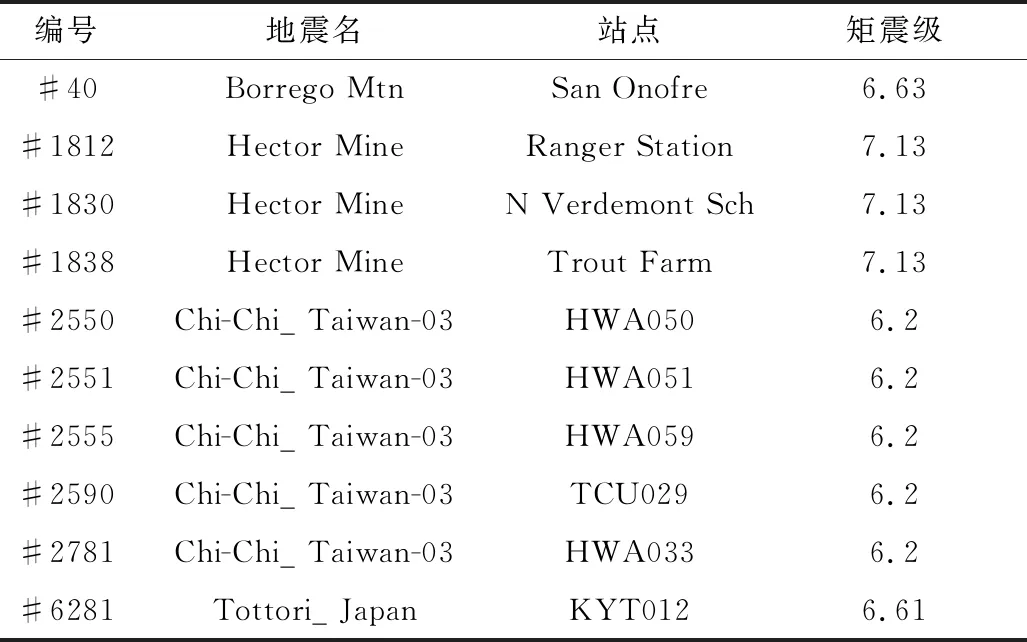
表6 地震动基本信息Table 6 Basic information of ground motion

设计反应谱以及选出的10条地震动反应谱，如图5所示。

3.2 指标分析参数的选取

DM指标度量是地震作用下反映结构动力响应和损伤程度的状态参数。对于框架结构，最常采用结构层间位移角的最大值θmax作为DM的指标度量[21]。IM指标度量是反映输入地震动本身强度值的参数指标，既可以用地震动运动相关参数表示，也可以用结构的最大反应相关参数表示[22]。前者常用地震动的峰值加速度PGA，后者常用结构在第1阶自振周期下谱加速度Sa值表示。对于中长周期结构，PGA度量指标的离散性干扰严重，而在结构的最大反应相关参数指标中，中长周期的结构与Sa关联度比较高[23]，所以，在中长周期的结构下对结果数据具有集中性整合的优点，Sa度量指标最为适合。由于采用了长周期的20层钢框架结构，所以，DM度量指标采用结构的最大层间位移角θmax，IM指标选择结构在第1阶自振周期下的谱加速度值Sa。

3.3 极限状态点的确定

作出IDA曲线之后，为了进行结构抗震性能评估，根据相应判别准则确定曲线上的极限状态点。基于IM准则的极限点状态判据为：当曲线上某一点的地震强度指标IM数值达到所规定的极限状态界限值时，即可视这一点为极限状态点。基于DM准则的极限点状态判据为：当曲线上某一点的结构损伤指标DM数值达到所规定的极限状态界限值时，即可视这一点为极限状态点。由于此极限状态点是某一确定结构自身的失稳倒塌极限状态点，不同于基于IM准则的极限点状态判据，对于多条不同的地震动记录都可以采用同一DM界限值[23]。

3.4 超越概率函数

文献[24-25]给出了对结构进行易损性分析时采用的工程结构需求参数在确定的地震动强度量值IM下，对结构某一性能水准能力L的超越概率函数P，如式(6)所示，得到结构需求参数m在该确定的地震动强度值IM下服从对数正态分布。

(6)

式中：Φ为标准正态分布的分布函数。

4 结构-阻尼器系统的易损性评估

4.1 基于位移的倒塌易损性评估

选取基于DM准则的极限点状态判据，中国规范[7]通过此准则规定了钢框架结构倒塌抗震分析时的最大弹塑性位移角为1/50，即为基于DM准则的极限点状态判据的倒塌极限状态点。

对无阻尼器结构、设置粘滞阻尼器、摩擦阻尼器和防屈曲支撑3类典型阻尼器结构分别用IDA方法进行分析，得到各情况下的结构IDA曲线，如图6所示。将各条地震动对应的倒塌点极限状态，根据谱加速度Sa数值由小到大的顺序进行结构在第1自振周期的谱加速度的累计概率分布的排序，并采用结合Matlab工具拟合式(6)得出结构的倒塌易损性曲线如图7所示。

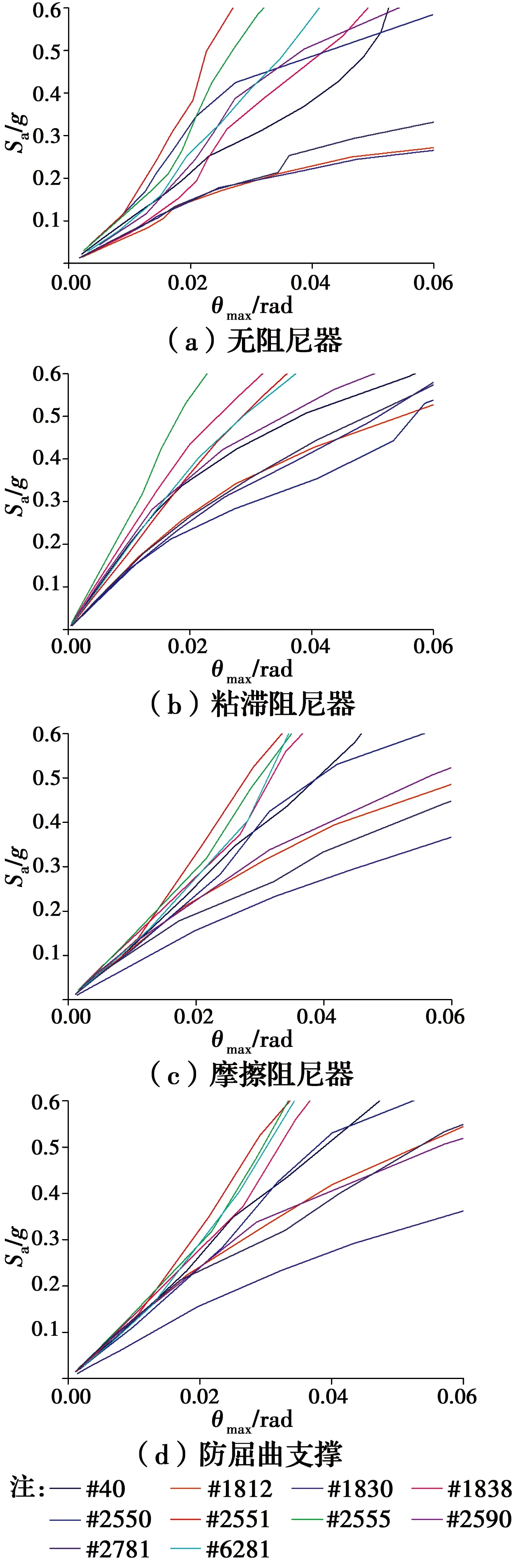
图6 结构倒塌的IDA曲线Fig.6 Structure collapse IDA

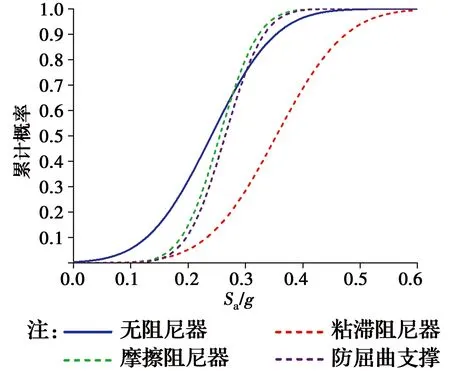
图7 结构的倒塌易损性曲线

为了对受阻尼器控制下结构的作用效果进行显著区分，采用CMR系数，即表征结构实际对地震的抗倒塌性能之于要求设防性能的存储潜力水平[26-27]，如式(7)所示。

(7)

即在20层钢框架结构的倒塌作用易损性曲线图所对应的横坐标谱加速度IM值在50%概率点处与遭遇罕遇地震时结构的谱加速度IM值的比值计算见表7。

表7 IM值的比值Table 7 The ratio of IM

在以同一减震目标控制在76%时设计出来的阻尼器中，对于结构在远场地震下的抗倒塌性能方面，粘滞阻尼器效果最佳，然后是防屈曲支撑，最后是摩擦阻尼器。但当谱加速度达到0.3g之后，防屈曲支撑和摩擦阻尼器的控制效果在很高的超越性能概率80%下会被无阻尼结构超越，这说明在控制结构的倒塌破坏性能时，防屈曲支撑和摩擦阻尼器并不能很好地起到控制作用，因此，在工程应用中，对于远场地震作用下的建筑结构，推荐设置粘滞阻尼器，以满足自身的抗倒塌性能。

4.2 基于位移的损伤性能水准评估

对比分析在出现结构损伤时设置典型阻尼器结构维持对应设计性能水准的能力，分别采用累积对数正态概率分布的函数关系对无阻尼器结构以及结构在粘滞阻尼器、摩擦阻尼器和防屈曲阻尼器下的IDA曲线，拟合了出现损伤破坏时性能量化指标下结构第1阶自振周期的谱加速度Sa的倒塌易损性概率曲线，拟合时采用的结构最大层间位移角对应结构的性能指标如表8所示。

表8 结构性能水准的判别Table 8 Destruction level reference

表8中，[Δue]指钢框架结构弹性层间位移角限值，[Δup]指钢框架结构塑性层间位移角限值。根据《建筑抗震设计规范》[13]的规定，多、高层钢结构的弹性层间位移角限值[Δue]取0.004，塑性层间位移角限值[Δup]取0.02。

如图8所示，控制结构最大层间位移角大于0.004而小于0.006(1.5[Δue])时，即控制结构轻微损伤性能中，阻尼器的控制效果为粘滞阻尼器最佳，防屈曲支撑稍逊色，摩擦阻尼器虽次之但差别不大；如图9所示，控制结构最大层间位移角大于0.006 而小于0.012(3[Δue])，即控制结构中等损伤性能中，阻尼器的控制效果为粘滞阻尼器最佳，防屈曲支撑稍逊色，摩擦阻尼器虽次之但差别不大；如图10所示，控制结构最大层间位移角大于0.012而小于0.018(0.9[Δue])时，即控制结构严重损伤的性能中，阻尼器的控制效果为粘滞阻尼器最佳，防屈曲支撑稍逊色，摩擦阻尼器虽次之但差别不大。

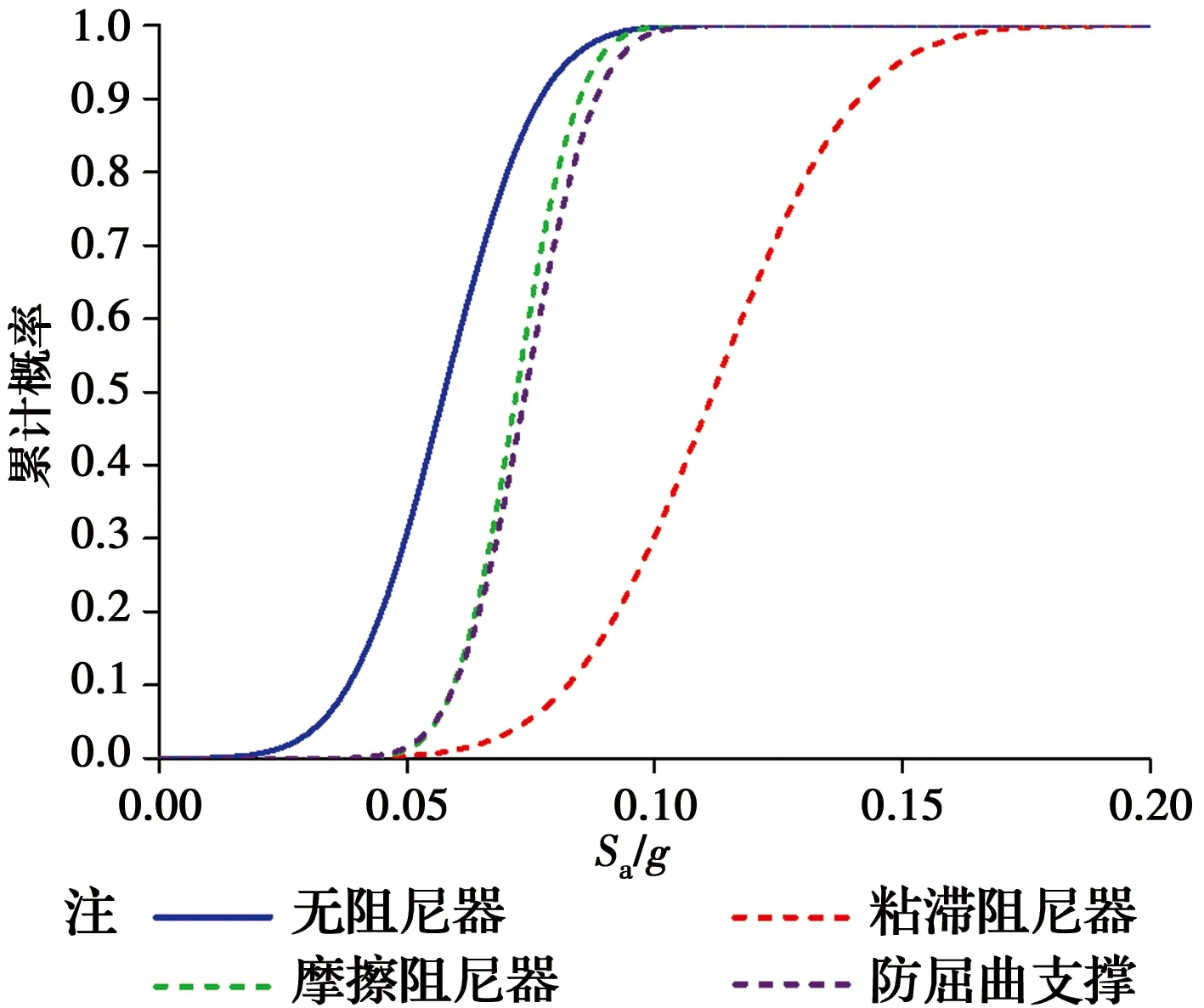
图8 轻微损伤性能的易损性曲线Fig.8 Seismic fragility with slight

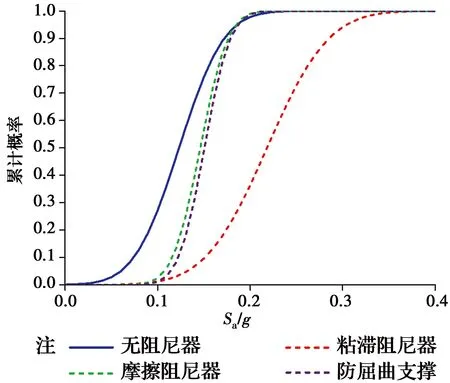
图9 中等破坏性能的易损性曲线Fig.9 Seismic fragility with medium

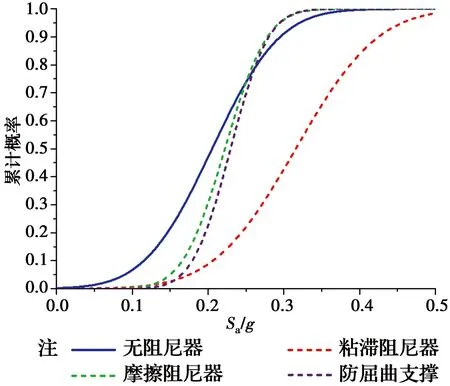
图10 严重破坏性能的易损性曲线Fig.10 Seismic fragility with severe

在3个性能指标水准下，粘滞阻尼器的表现最为突出。虽然防屈曲支撑稍比摩擦阻尼器更优，但防屈曲支撑和摩擦阻尼器两者表现的控制结构的性能效果差别不大，但需要注意的是，随着性能水准程度的提升，防屈曲支撑和摩擦阻尼器的控制效果甚至在很高的超越性能概率(中等破坏时为95%，严重破坏时为83%)下会被无阻尼结构超越，这说明在控制结构中等损伤和严重破坏的结构性能水准控制范围内，防屈曲支撑和摩擦的控制效果不是很好，但在轻微损伤的结构性能水准下，结构控制性能明显。

5 结论

研究了基于中国现行抗震规范所设计的高层建筑-阻尼器系统的地震易损性，评估了中国规范所设计的3类典型阻尼器的实际性能。所得结论如下：

1)采用基于位移的性能水准评估指标，与规范中阻尼器设计所选用的指标一致，通过IDA分析指出规范所设计阻尼器的实际性能在某些强地震下可能劣于无阻尼器建筑，且不同类型阻尼器的减震效果也有所差异，尤其是速度型和位移型阻尼器差异明显。

2)基于中国规范建立的20层钢结构Benchmark模型和中国规范所设计阻尼器，在同一减震设计目标需求下，从抵抗结构的抗倒塌概率来看，粘滞阻尼器表现最优，防屈曲支撑和摩擦阻尼器次之，且二者性能接近。

3)采用体现性能水准的结构位移为评价指标时，粘滞阻尼器表现最优，防屈曲支撑虽然略高于摩擦阻尼器，但两者差别不大，在较强地震作用下，出现了设置防屈曲支撑和摩擦阻尼器的结构性能控制效果稍逊原始结构的情况。