基于Isight的倾转旋翼飞行器前飞状态翼型优化

赵广，何国毅，王琦，罗云，王振

(南昌航空大学 飞行器工程学院，南昌 330063)

0 引 言

倾转旋翼飞行器不仅具有直升机的垂直起降(VTOL)能力，同时拥有固定翼飞机的高速、长航程特点，被认为是下一代旋翼类飞行器的主要发展方向[1]。机翼作为飞行器的核心部件，其设计很大程度上决定了飞行器的性能。开展对倾转旋翼飞行器机翼的气动优化设计，对于提高倾转旋翼飞行器飞行性能具有重要意义。

目前，国内外已在倾转旋翼飞行器的优化方面做了大量研究。国外，L.Vigevano等[2]总结了NICETRIP项目进行的倾转旋翼飞行器ERICA的气动特性分析和一些部件(例如机身/机翼整流罩、机翼等)的优化设计，在对机翼进行优化时，根据旋翼滑流的影响，将机翼分为固定段(层流翼型)和倾转段(湍流翼型)，认为同时结合两种翼型的机翼可实现明显的减阻效果，但未指出具体的优化过程；M.K.Lee等[3]和R.L.T.Bevan等[4]通过在机翼上安装一些附属装置提高飞行性能，例如在发动机短舱外再增加一小段机翼，虽然机身重量略微增加，但机翼升阻比却得以显著提高，或者在机翼上安装涡流发生器，与干净机翼相比，可在减阻的同时减少气流分离；M.Kim等[5]采用主动控制的方法，悬停模式在前缘和后缘同时使用射流，可减少机翼所受下洗载荷；倾转模式只需在前缘使用射流，可使阻力明显减小。

国内，针对倾转旋翼飞行器的机翼优化的研究主要有：徐家宽等[6]、孙凯军等[7]指出处在滑流影响下的机翼等部件与无滑流影响区域的流场特征不同，螺旋桨滑流会对机翼升阻特性产生显著影响。王科雷等[8]认为机翼优化时不考虑滑流影响，实际工作状态与设计点存在偏离，导致气动特性得不到提升。朱秋娴等[9]根据前飞状态下旋翼/机身/短舱对机翼影响沿展向的分布，将机翼分成三段，在每段取特征剖面采用代理模型进行优化，优化后全机升阻比增大了36.78%，但优化细节未给出。

综上，目前对于倾转旋翼飞行器机翼优化方面涉及具体方法的研究仍较少。本文在前人研究的基础上，根据“由于旋翼存在，导致前飞时机翼展向位置气动环境不同”这一实际，将机翼分为内外两段，在每段选取代表性截面，并选择截面上的速度表征两段机翼气动环境的不同，优化前飞状态两段机翼翼型；通过对比两种速度设定的优化效果，以期为倾转旋翼飞行器的气动布局设计提供一些有参考意义的结论。

1 流场求解方法

在直角坐标系下求解带有动量源项的RANS方程：

(1)

其中，

式中：ρ、p、E、H分别为气体的密度、压强、总能和总焓；V=[u,v,w]T为气体的绝对速度；J为动量源项。

2 动量源方法及验证

由于精确求解旋翼需要在桨叶几何上生成贴体网格，会导致网格数目过大，耗费大量的计算资源。采用动量源方法时，旋翼用作用盘代替，桨叶对气流的作用以动量源代替。可大幅降低网格数量，提高计算效率。

作用盘即在旋翼叶片扫过的区域由一些有限厚度的网格组成。动量源即在作用盘区域每个网格中引入表示叶片对周围气体的作用力。作用盘方向对应实际的旋翼桨盘方向。作用盘半径对应实际桨叶半径。动量源S可表示为

(2)

式中：Nb为桨叶数量；F为桨叶微段所受的气动力，其计算基于叶素理论；Δτ为桨叶扫过该网格单元时所转过的角度；Vcell为网格单元的体积。

为了验证动量源的计算精度，计算文献[10]的算例，对比结果如图1所示，图1(a)和图1(b)分别为桨盘下方不同位置处的动压对比。

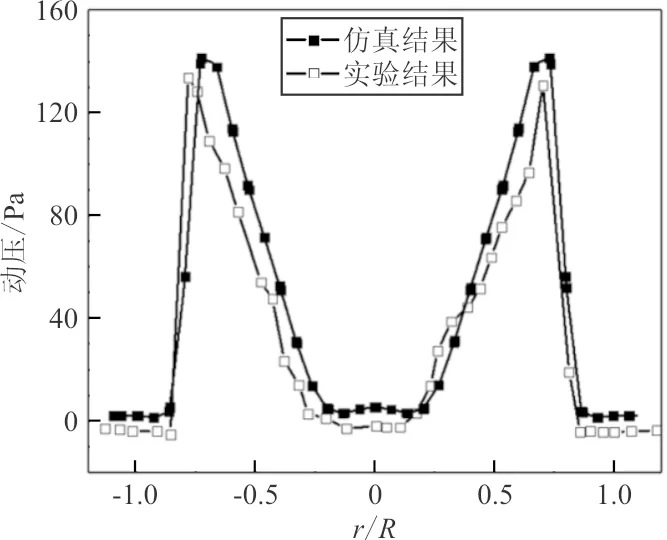
(a)y=0.215R

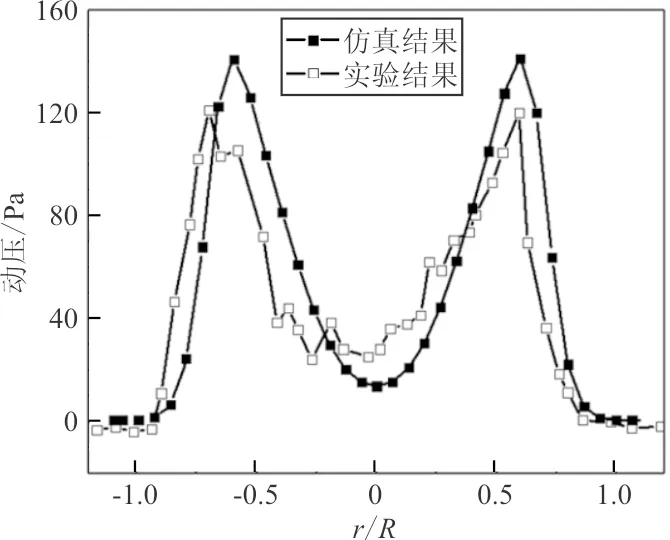
(b)y=0.660R图1 旋翼下方动压分布与实验的对比Fig.1 Comparison of the dynamic pressure distribution under rotor with experiment

从图1可以看出：动量源结果与文献的实验值趋势一致，且结果较为接近，因为本文选取旋翼后方代表性截面的速度分布做优化，此算例表明动量源方法可以较为准确地模拟旋翼下方的动压(速度)分布。

3 物理模型及准确性验证

3.1 物理模型

本文在倾转旋翼飞行器前飞状态下进行优化，为了减小计算量，采用半翼展模型，如图2所示，旋翼用作用盘(Actuator Disk)代替。

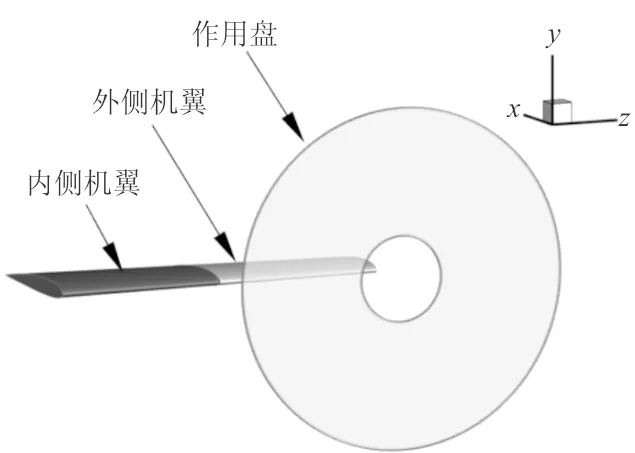
图2 倾转旋翼飞行器半翼展模型Fig.2 Half wingspan model of tiltrotor aircraft

由于旋翼的影响，机翼可分为内侧机翼(Inner Wing)自由来流区和外侧机翼(Outer Wing)旋翼尾流区[11]，如图3所示。旋翼半径和两段机翼展长均为R。优化前两段机翼翼型均为NACA2412。

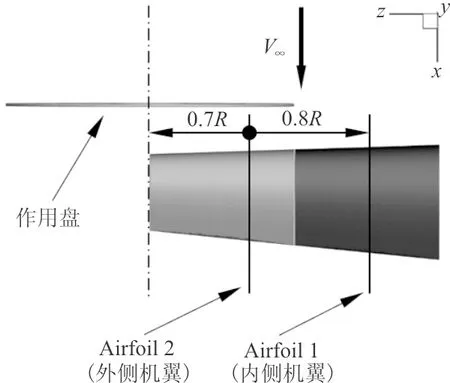
图3 倾转旋翼飞行器机翼优化截面的选取Fig.3 Optimization section selection of the wing of tiltrotor aircraft

根据两段机翼所处来流速度的不同，取每段机翼的代表性截面，对二维翼型NACA2412进行优化，分别得到翼型Arifoil 1、Airfoil 2，再将优化后的翼型各自拉伸成内侧机翼和外侧机翼。因为桨叶的0.7R处特征剖面的空气动力学特性具有代表性[12]，对于外侧机翼，取桨叶上此特征剖面对应在机翼上的位置为代表性截面，即图3所示的0.7R。对于内侧机翼，可视为处于自由来流中，可取机翼中段为代表性截面，即图3中的0.8R。

本文在V∞=15 m/s，旋翼前进比λ=0.1(λ=V∞/(Ω×R)，Ω为旋翼角速度)，机翼攻角α=0°的工况下优化的，以升阻比K最大为优化目标。优化前需先得出Arifoil 1、Airfoil 2的升力和阻力值。为了说明本文所用方法的有效性，采用两种速度设定优化。设定一：优化时不考虑旋翼的影响，内侧机翼和外侧机翼翼型入口边界速度均为15 m/s；设定二：优化时考虑旋翼的影响，内侧机翼翼型入口边界速度为15 m/s，外侧机翼翼型入口边界速度根据桨盘后方实际气流速度，采用大小随位置变化的非均匀来流，如图4所示。计算域y方向大小根据径向0.7R处所取截面在桨盘上对应的实际长度确定，如图5所示。这两种设定的区别在于对外侧机翼翼型优化时边界条件的选择。

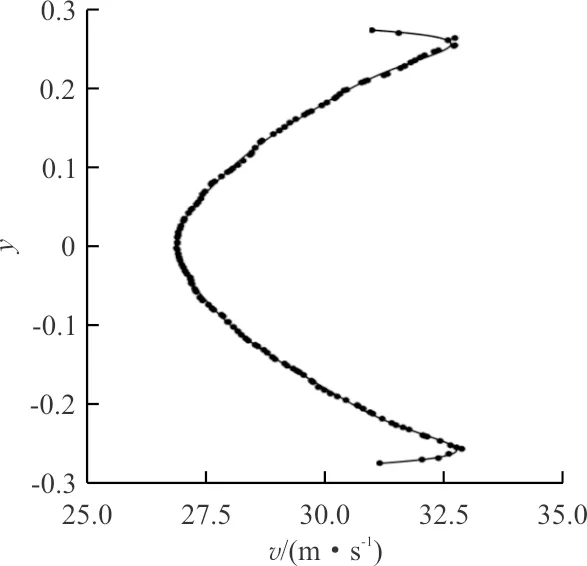
图4 外侧机翼入口速度分布Fig.4 Outer wing inlet velocity distribution

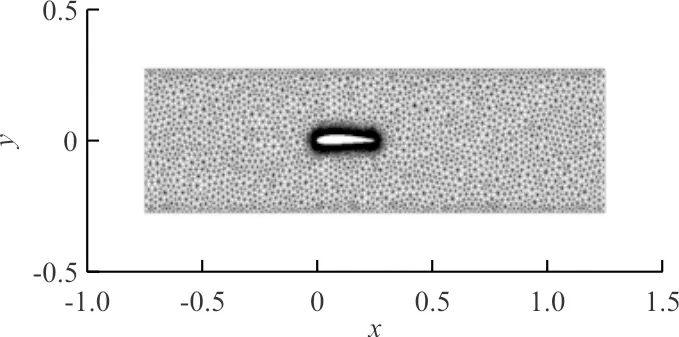
图5 外侧机翼计算域网格Fig.5 Outer wing computational domain mesh

3.2 计算精度验证

对二维翼型优化前，需计算翼型的升阻力系数。根据文献[13]提供的NACA4418翼型实验数据，进行模拟计算。不同攻角下翼型升阻力系数与实验值的对比如图6所示，可以看出：计算值与实验值较为吻合。

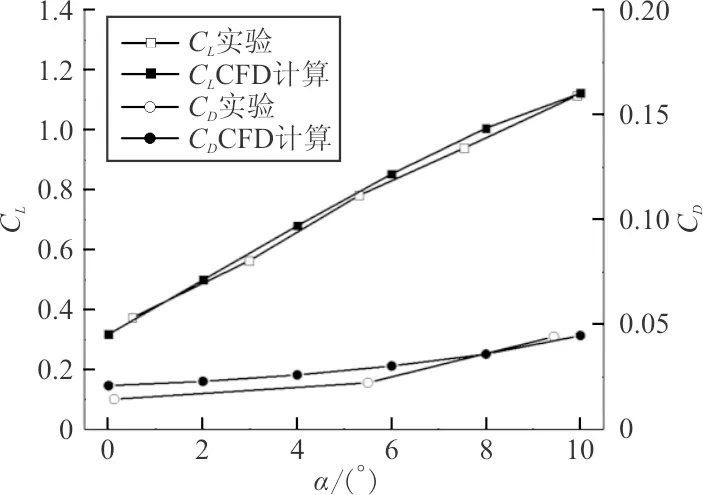
图6 计算精度验证Fig.6 Verification of computational accuracy

3.3 网格无关性验证

为了排除网格对优化结果的影响，计算四套网格，网格数分别为Mesh1(110万)、Mesh2(142万)、Mesh3(175万)和Mesh4(202万)。网格定义和分布如图7和表1所示，其中Ex、Ez分别为机翼弦向和展向边上的节点数，Δs为边界层第一层网格高度。

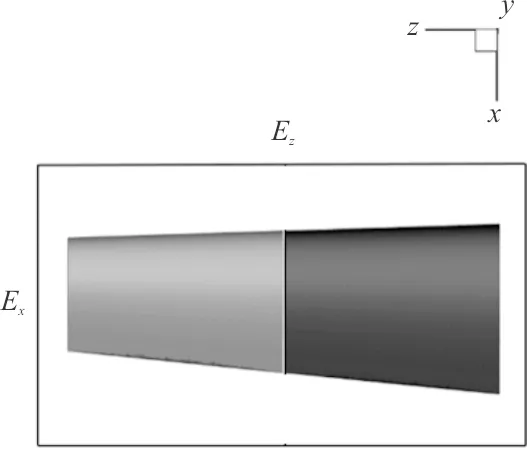
图7 机翼几何网格节点定义Fig.7 Definition of wing geometric mesh node

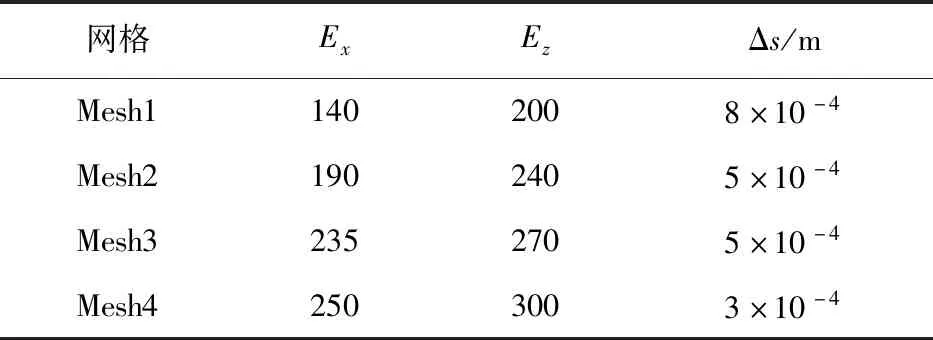
表1 四套网格的网格分布Table 1 Distribution of four sets of meshes

四套网格的计算结果如图8所示。

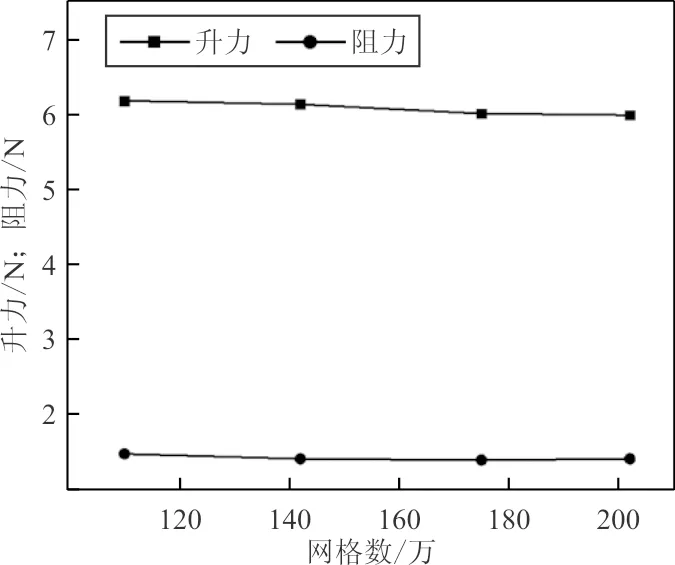
图8 四套网格升力、阻力计算结果Fig.8 Four sets of grid lift and drag calculation

从图8可以看出：当网格数增加到175万时，升力和阻力的波动已经很小，可认为计算结果几乎不随网格数目的变化而变化。为了兼顾计算精度和计算代价，本文选取Mesh3(175万)网格计算。

4 翼型几何参数化

在对翼型进行优化设计时，直接改变的是控制翼型生成的参数，进而实现翼型形状更新。因此必须进行翼型参数化描述。

考虑到Hicks-Henne型函数方法应用广泛，具有描述翼型精确、曲线平滑的优点[14]，本文采用以Hicks-Henne 为型函数的线性扰动法，即新翼型的几何形状由原始翼型和扰动的线性叠加来表示。

(3)

式中：yup、ylow分别为新翼型的上下翼面函数；yup0、ylow0分别为原始翼型的上下翼面函数；h为控制翼型生成的设计变量的个数。

理论上，设计变量h的个数越多，设计空间越大，但同时计算量也会极大增加，通常单个翼面h=4～9为宜[14]。本文取h=6，即翼型上下翼面各有6个设计变量用于改变翼型形状。以型函数fh(x)的系数ah、ah+6(h分别为1,2,3,4,5,6)表示上下翼面控制翼型形状的设计变量。ah的取值范围为[-0.01 ,0.05]，ah+6的取值范围为[-0.05,0.01]。

采用改进的Hicks-Henne型函数fh(x)[15]。

(4)

式中：e(h)=ln0.5/lnxh。

取xh(h分别为1,2,3,4,5,6)分别为0.15,0.30,0.45,0.60,0.75,0.90。

Hicks-Henne方法得到的翼型曲线如图9所示。A1、A2为设计变量ah组成的向量。其中A1=[0,0,0,0.05,0.05,0.05,0,0,0,-0.05,-0.05,-0.05]T,A2=[0.05,0.05,0.05,0,0,0,-0.05,-0.05,-0.05,0,0,0]T。

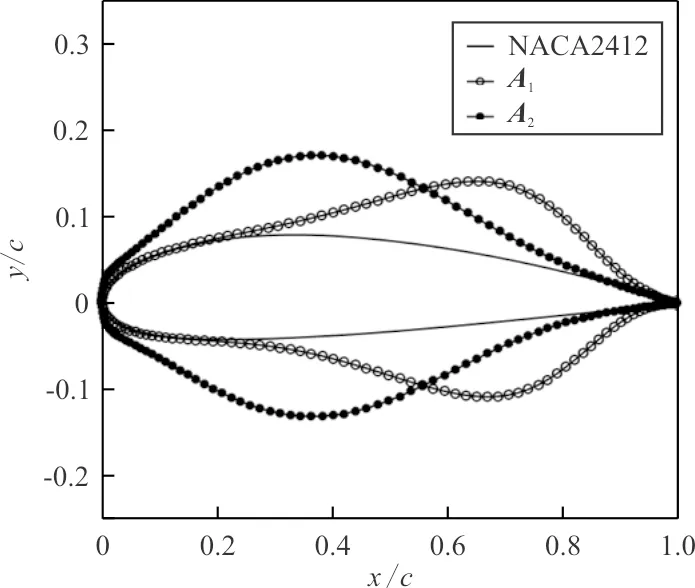
图9 Hicks-Henne 方法得到的翼型曲线Fig.9 Airfoil curves generated by Hicks-Henne method

从图9可以看出：三组翼面曲线连续平滑，即使在翼型前缘和后缘均有较大的扰动量，表明采用改进的Hicks-Henne型函数能够满足对翼型参数化的要求。

5 基于Isight的优化设计流程

Isight优化流程如图10所示，采用Isight优化平台集成翼型几何生成(MATLAB 程序)、网格划分(Pointwise)和流场求解(Fluent)等软件，实现翼型自动优化。

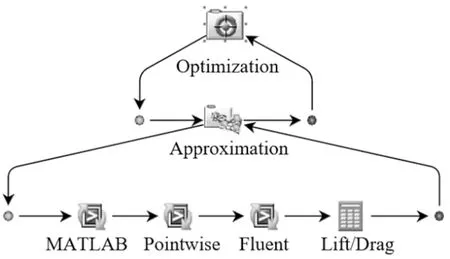
图10 Isight优化流程Fig.10 Isight optimization process

代理模型的创建主要包括样本数据采集和代理模型的选择。本文采用最优拉丁超立方设计(Opt LHD)方法生成300个样本点构造模型，另用115个样本点用于误差分析，对升阻比K建立代理模型。代理模型选RBF模型，该模型的优点是具有较强的拟合复杂非线性函数的能力。RBF代理模型精度分析如表2所示。

表2 RBF代理模型精度分析Table 2 RBF precision analysis of surrogate model

代理模型生成后一定要查看可信度，一般要求均方根误差RSME小于0.2，相关系数R2大于0.9[16]。从表2可以看出：RSME小于0.2，且R2值较为接近0.9，因此认为建立的代理模型具有较高的可信度，可代替数值仿真实现优化。

优化组件采用多岛遗传算法(MIGA)，子群规模为10，岛(子群)个数为10，总进化代数为10。

6 翼型优化结果及分析

对于外侧机翼，由于优化时采用的边界条件不同，即使是同一目标函数，优化后得到的翼型气动外形也不同。优化后的外侧机翼如图11所示，可以看出：与原始翼型NACA2412对比，采用设定一得到的外侧机翼优化翼型明显变厚，翼型后半段下翼面上凸；设定二得到的外侧机翼优化翼型弯度明显增大，厚度与原始翼型相比略有减少。

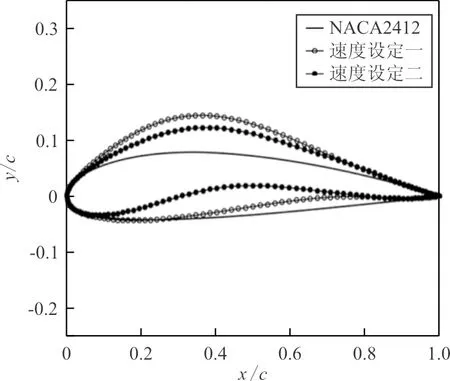
图11 外侧机翼优化翼型与原始翼型的对比Fig.11 Comparison of optimized airfoil and original airfoil of outer wing

外侧机翼翼型压力云图如图12所示，可以看出：翼型上翼面上凸带来了更大的低压区；并且优化后的翼型下翼面上凸部分出现高压区，有利于提高升力系数。采用两种速度设定优化的翼型弯度都比原始翼型更大，翼型弯度变大增大了翼型的有效攻角，增加了升力系数。

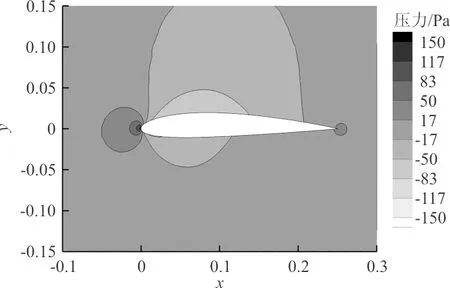
(a)原始翼型

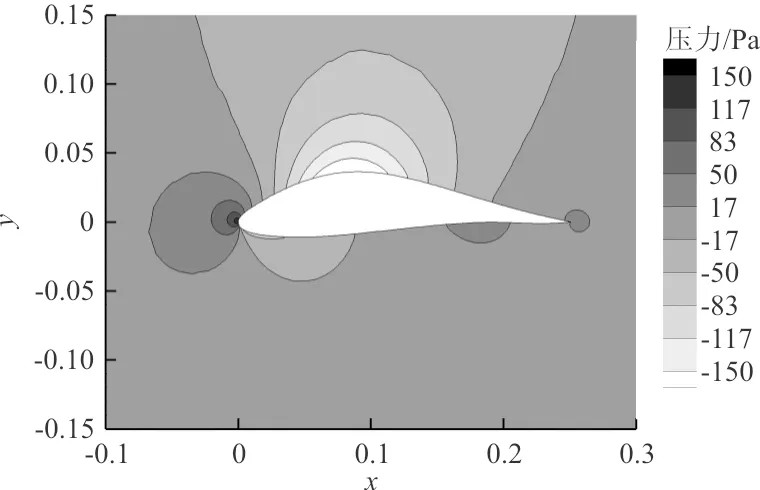
(b)速度设定一

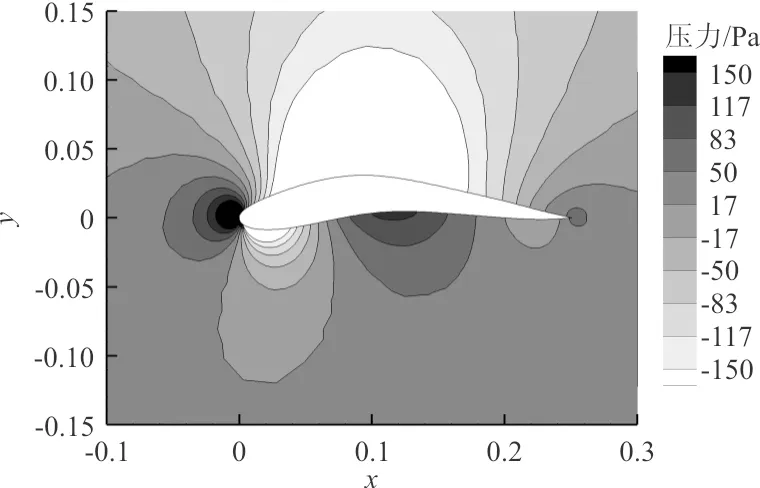
(c)速度设定二图12 外侧机翼翼型的压力分布Fig.12 Pressure distribution of outer wing airfoil

将优化后的翼型应用到三维机翼上，优化前后气动性能对比如表3所示。

表3 优化前后倾转旋翼飞行器气动性能对比Table 3 Aerodynamic performance comparison of tiltrotor aircraft before and after optimization

从表3可以看出：两种速度设定虽然优化后阻力系数增大，但升力系数增加幅度更大，都能提高机翼的升阻比；对比两种速度设定，设定二优化的翼型生成的三维机翼升力系数与设定一相当，但阻力系数更小。

上述优化结果是在攻角α为0°时得到的。倾转旋翼机前飞时有不同的飞行状态，因此本文计算攻角从0°～ 7°范围内优化前后机翼的升阻比，如图13所示。

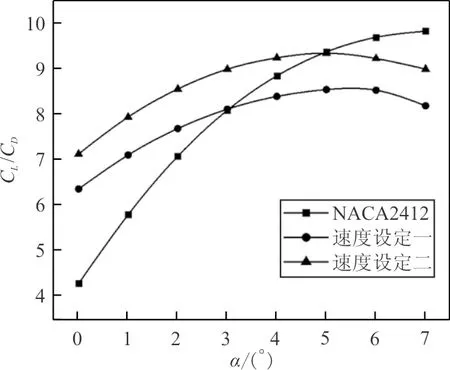
图13 倾转旋翼飞行器机翼升阻比优化前后对比Fig.13 Comparison of lift drag ratio of wing before and after optimization of tiltrotor aircraft

从图13可以看出：在有限的攻角范围内,两种速度设定均能起到优化作用，对升阻比的提升率随攻角增大而减小，且设定二的优化效果好于设定一；对于速度设定二，当攻角小于5°时，对升阻比有提升作用；而对于速度设定一，当攻角大于3°时，已经不能提高机翼升阻比。

7 结 论

(1)优化后的机翼升阻比提高，表明本文建立的基于Isight自动优化平台及代理模型的方法适用于倾转旋翼飞行器的翼型优化。

(2)本文所用的动量源方法，将旋翼桨叶对空气的周期性扰动通过时间平均的方法转化为“准定常”流动，该方法能在较大程度上模拟旋翼下洗流场特性。

(3)对比两种速度设定，设定一没有考虑旋翼的影响，设定二的边界条件是根据旋翼后方的实际气流速度确定的。设定二采用的边界条件更符合实际，在0°攻角时，比设定一优化的翼型生成的机翼升阻比更大，且能在较大的攻角范围内提高机翼升阻比。