飞机结构有限元分析中分布载荷的离散化处理算法

尹建军，李高胜，姚雄华

(1.航空工业第一飞机设计研究院 结构设计所，西安 710089)(2.航空工业第一飞机设计研究院 总设计师办公室，西安 710089)

0 引 言

在航空领域，有限元分析已经成为现代飞机结构设计中必不可少的重要一环。有限元方法的本质是，把实际结构由连续弹性体受分布体力和分布面力作用下求解位移场的无限自由度问题，转换成离散结构仅在结点处受结点载荷作用，求各结点位移的有限自由度问题[1-3]。因此，有限元法分析第一个步骤即为离散化，包括结构的离散化和载荷的离散化。载荷的离散化是把单元内部的集中力、分布力按照静力等效的原则移置到结点上，成为等效结点载荷。

由于结构强度、气动弹性等设计工作中对载荷离散化的大量应用需求，尤其在气动弹性设计时，需要将每一次迭代结果的气动载荷施加到结构结点上。通常是在气动结点上直接积分，得到气动载荷的集中力，然后通过样条插值得到结构网格上的等效载荷值[4-5]。国内对该方面开展的研究较多。王专利[6]通过飞机升降舵的实例证明了“多点排”气动载荷分配算法的效率和精度；尹晶等[7]根据飞机机翼剖面气动力载荷分布的基本规律,在已知剖面载荷总量、合力作用点位置及给定剖面弦长的条件下,提出一套转轴椭圆和转轴抛物线的几何算法,利用编程计算快速给出压力载荷分布沿弦长的几何描述,继而可快速地分配到翼剖面结构结点上；高尚君等[8]采用基于弹簧-悬臂梁物理模型的最小变形能的载荷转换方法，解决了载荷转换前后结点重合引起的无法计算的问题；胡亮文等[9]构造了三种不同形式的压力场曲面函数，通过积分求得任意微元面积内的气动力及其作用点，按照最小变形能原理将积分得到的气动载荷分配到有限元结点上；雷莉等[10]对传统的三点排[11]、四点排[12]和多点排[11]方法进行对比，得到不同方法转换后的结构有限元结点载荷，三种方法都可以模拟气动载荷，其中多点排效果最优；张建刚等[13]根据原始气动压力点数值，采用样条曲面拟合方法得到翼面压力分布曲面及有限元结点上的压力值，在有限元模型单元上积分得到有限元结点载荷。此外，还研发了不同的载荷转换方法[14-15]。

三点排的效率高，但三个有限元结点需满足如下要求：三个有限元结点与待转换载荷结点距离最近，三个有限元结点不共线，待转换载荷结点位于三个有限元结点所围区域之中。为了满足上述要求，会牺牲一定的效率。多点排方法效率偏低，当选取的结点数量较多时，计算耗时巨大。对于三点排、四点排及多点排方法，计算过程中会用到待转换载荷结点与有限元结点之间的间距，当待转换载荷结点位于结点上的时间距为零，作为分母程序报错。为了避免错误，会人为引入一定误差。

本文利用薄板弯曲单元理论，针对飞机结构设计中需要进行离散化处理的两种不同类型的载荷数据，提出分布载荷离散化处理的算法，并对实际应用中舍弃结点载荷力矩分量处理方法的合理性进行说明。

1 分布载荷数据类型

1.1 气动载荷

在飞机设计院所中，气动载荷一般由气动力载荷专业提供给结构强度专业设计人员用于有限元分析，其形式为气动力网点上的气动力载荷列阵。气动力网点，通常是展向等百分线与若干弦向控制线相交形成的网点群(气动力)[2]。气动分布载荷数据一般以文本文件或数据库形式提供给结构强度专业，该数据包含以下信息：

(1)气动力网点坐标及相应坐标系；

(2)载荷设计工况代号及相应的飞机状态参数(包括飞机重量，滚转、俯仰、偏航角速度和角加速度，过载，速压等)；

(3)气动力网点上的气动力载荷列阵(上、下表面的压力系数)。

在气动力网格尺寸足够小的情况下，可以认为气动力网点处的压力均匀作用在对应的微元上，用网点压力系数乘以速压可以获得该气动力网点处的气动力，该力为作用在网点上的集中力。即气动力载荷专业提供的数据实际已经将连续分布的气动力离散化为有限的集中载荷，结构有限元载荷的离散化处理本质上是把单元上的非结点集中载荷按静力等效原则移置到结点上。

1.2 惯性载荷

惯性载荷是由质量分布数据与过载相乘得到的。质量分布数据由重量专业提供，数据形式为质量网点上的质量列阵。质量分布通常是不规则的，考虑计算需要，重量专业按照规定的方法选定适当数量的质量网点，然后把所有结构和非结构质量按质量等效原则堆聚到质量网点上，形成质量列阵[2]。质量分布数据包含以下信息：

(1)质量网点坐标及相应的坐标系；

(2)质量网点上的质量数据。

从结构有限元分布载荷离散化处理的角度看，惯性载荷具有与气动载荷同样的特点，即已经离散化为集中力点集，离散化处理的目标是把不在结点上的载荷移置到结点上。

1.3 压差载荷

座舱、客舱等有乘员的舱室，燃油箱内部等空间一般需要增压，壁板和框、梁腹板要承受分布的内外压差载荷。压差载荷的特点是沿结构表面的法向作用，均匀分布。这是一种简单的分布面力，压差集度为常数。

1.4 液体压力载荷

水上飞机的水下部分、燃油箱、汲水容器等结构会受到液体压力作用。液体压力随深度按线性规律分布，即p=ρgh。

综上所述，飞机结构有限元分析需对两类载荷进行离散化处理：其一为上游专业提供的网点载荷列阵数据；其二为以均布或线性分布等简单形式作用的面载荷。

2 单元类型与特点

2.1 单元形状

飞机结构一般为薄壁结构，外形曲面由多个平面近似，通常按由桁条与肋、框划分成的实际格子来划分单元，这样可以更加真实地模拟各结构元件的承载功能，且更易于结果分析。利用矩形、任意四边形和三角形单元组成的网格可以近似任何薄壁结构。

2.2 单元承载特点

当薄板承受一般载荷时，总可以把每一个载荷分解为两个分载荷，一个是作用在薄板中面之内的纵向载荷，另一个是垂直于中面的横向载荷。对于纵向载荷，可以认为它们沿薄板厚度均匀分布，因而它们所引起的应力、形变和位移，可以按平面应力问题进行计算。横向载荷将使薄板弯曲，它们所引起的应力、形变和位移，可以按薄板弯曲问题进行计算[1]。

在飞机结构设计中，大量应用薄壁构件，例如壁板蒙皮及框、梁、肋的腹板等，它们在结构有限元模型中简化为平板单元，按承载特点分为两种单元：一是平面应力单元，另一种是薄板单元。

平面应力单元基于弹性力学平面问题理论，每个结点的位移、应变、应力、结点力都是在平面内的，单元与单元之间结点是铰接的，结点载荷只有力分量没有力矩分量。平面应力单元不能承受面外载荷。在飞机结构有限元模型中，采用平面应力单元的区域，面外力由单元周边布置的杆、梁等单元承受。

薄板单元基于弹性力学薄板弯曲理论，相邻单元之间有法向力和力矩的传送，因此必须把结点当成刚性连接的。每个结点具有3个参数(3个自由度)：1个线位移(挠度w)和2个角位移(绕x轴的转角θx，绕y轴的转角θy)。即

(1)

对应的结点力为

(2)

3 等效结点载荷

3.1 基本原理

在有限元分析中，认为单元与单元之间仅通过结点相互联系。因此，在结构离散化过程中，如果外载荷不是直接作用在结点上，那么就需要将非结点载荷向结点等效移置。即把作用在结构上的真实外载荷理想化为作用在结点上的集中载荷。

整个结构的非结点载荷的移置按单元进行，即将各单元所受的非结点外载荷分别移置到各单元相应的结点上；然后，在公共结点处应用力的叠加原理，便可求出整个结构的结点载荷列阵。因此只需解决单元载荷移置问题就解决了整个结构的载荷移置。

单元载荷移置所遵循的原则是能量等效原则，即单元的实际载荷与移置后的结点载荷在相应的虚位移上所做的功相等。

对集中力有

Re=NTP

(3)

对面力有

Re=∬ΩeNTqdxdy

(4)

3.2 网点载荷列阵移置

网点载荷列阵按集中力处理，将单元内部的载荷点逐一按照公式(3)移置到单元的结点上，再将其全部叠加就获得了等效结点载荷。

矩形薄板单元如图1所示，将位移模式代入式(3)并计算整理后，有

(5)

(6)

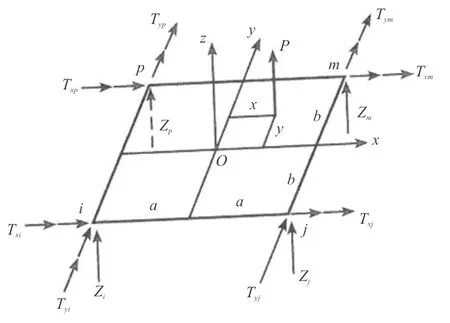
图1 矩形薄板单元Fig.1 Rectangular thin plate element

对任意四边形薄板单元，通过坐标变换，将整体坐标系下的任意四边形映射到局部坐标系的单位正方形单元，如图2所示。

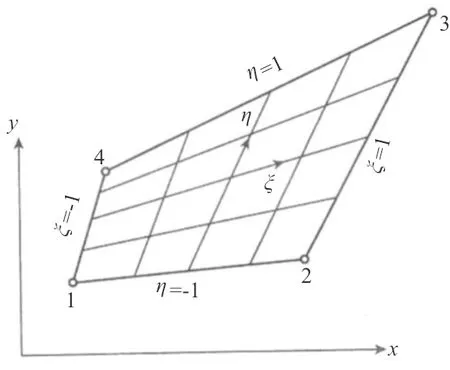
(a)映射前单元

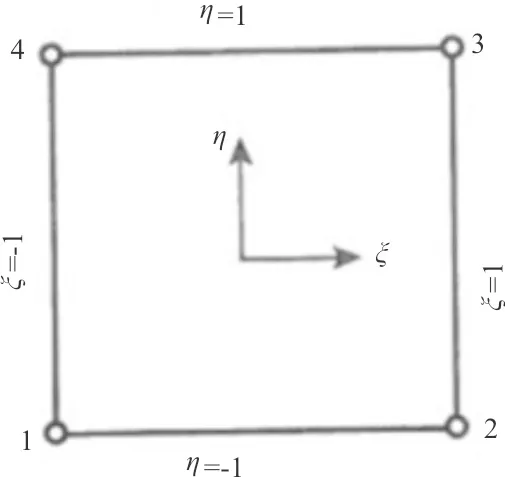
(b)映射后单元图2 任意四边形映射为单元正方形Fig.2 An arbitrary quadrilateral mapped to a unit square

当假定结点载荷的力矩分量为零时，等效结点载荷为

(7)

(8)

(9)

式中：Ni为形函数；|J|为整体坐标(x，y)与局部坐标(ξ，η)的雅可比行列式。

三角形薄板单元如图3所示，采用面积坐标按式(10)获得形函数，代入式(3)即可得到载荷移置的解。

N=[NiNjNm]

=[NiNxiNyiNjNxjNyjNmNxmNym]

(10)

(11)

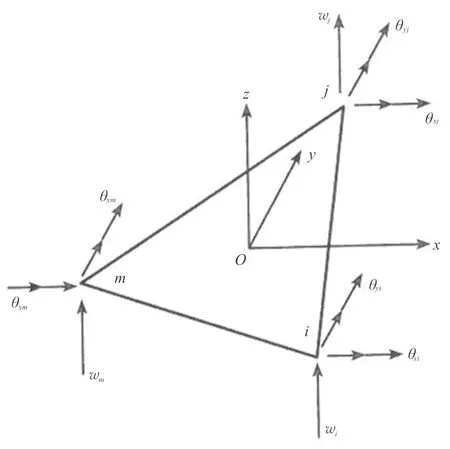
图3 三角形薄板单元Fig.3 Triangular thin plate element

3.3 简单分布面力的移置

对矩形薄板单元(图1)，当单元上受均匀分布载荷时，设载荷集度为常量q0，由式(4)计算整理可得

(12)

如果单元承受在x方向线性变化的法向载荷，则需要对分布函数积分。

任意四边形单元和三角形单元受简单分布载荷的处理方法与矩形单元类似。

3.4 力矩分量的处理

移置到各结点的载荷中，力矩载荷随着单元尺寸的减小而减小，在较小的单元中，它们对位移及内力的影响远小于法向载荷的影响，因此，在实际计算时，可以将力矩载荷略去不计[3]。但是，在飞机结构有限元模型中，单元按结构实际格子划分时，尺寸并不小，按上述处理方式获得的结点载荷力矩分量也很大。如果观察该结点相邻单元的结点载荷力矩分量，可以看出它们是相互抵消的。因此，在承受分布力的结构内部，有限元结点的力矩载荷仍可忽略不计，但是在边界区域，例如增压舱与非增压舱界面处，则不能忽略。

4 算例分析

4.1 简单算例

取长度1 000(x方向)，宽度100(y方向)平面板，受均匀分布的面外载荷。分布载荷作用点为2×2网格结点，单个结点上的载荷为1。

结构网格大小10×10，转换前后载荷云图如图4所示。

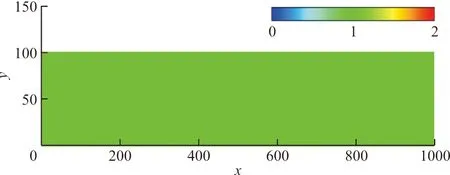
(a)转换前载荷分布

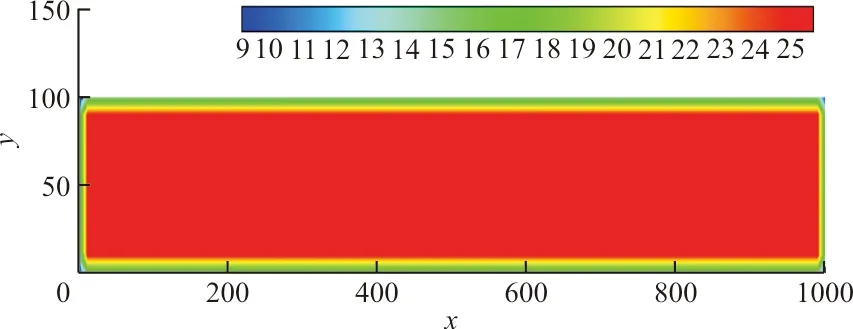
(b)转换后载荷分布图4 均布载荷转换前后对比Fig.4 Contrast before and after uniform load conversion

从图4可以看出：转换后载荷分布与转换前相一致，量值为转换前结点载荷的25倍，转换后载荷在边缘结点上的值偏小。

考虑三类结构网格单元：A类单元为内部网格单元，B类单元为边缘网格单元，C类单元为角部网格单元。与每个结构网格单元相关的气动结点单元关系如图5所示。

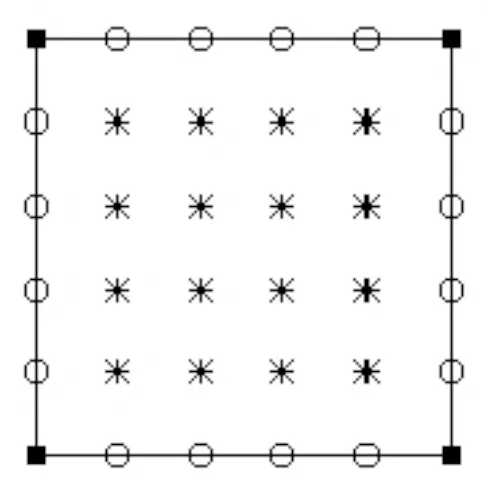
图5 典型有限元单元内部载荷点分布Fig.5 Load point distribution in typical finite element

对于A类单元，落在单元内部的气动结点(图中米字结点)，其全部载荷均作用在单元内；对于边缘气动结点(图中圆圈结点)，其载荷值的一半作用在单元内；对于角部气动结点(图中方实心结点)，其载荷值的四分之一作用在单元内。当气动结点上为均布载荷时(假设为1)，单元上的载荷总和为25。每个结点由4个单元公用，每个单元包含4个单元，转换到每个结点上的载荷理论为25。

对于B类单元，单元某一边缘上的气动结点全部作用在单元内，单元上的载荷总和为27.5。边缘上的两个结点只有两个单元的载荷对其有影响，已知内部两个结点载荷为25，边缘结点载荷为15。

对于C类单元，单元两个边缘上的气动结点全部作用在单元内，单元上的载荷总和为30.25，已知内部结点和边缘结点载荷分别为25和15，角结点上的载荷为9。

转换后载荷大小与理论值相一致。

采用同样的方法，分析沿x方向线性分布的面外载荷，载荷大小为F=0.01x。

得到转换前后的载荷分布如图6所示，可以看出：载荷分布与转换前相一致。

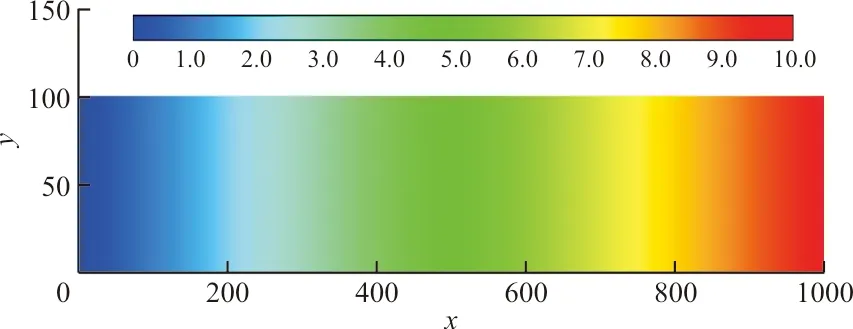
(a)转换前载荷分布

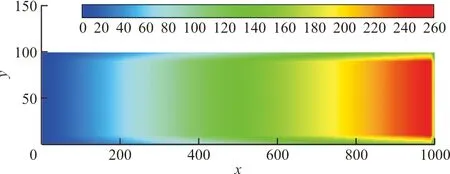
(b)转换后载荷分布图6 线性分布载荷转换前后对比Fig.6 Contrast before and after linear distribution load conversion

4.2 工程算例

取某大展弦比机翼翼载进行转换分析。输入数据为气动专业提供的翼面上压力系数分布及对应速压，通过转换得到结构有限元网格上的结点载荷。

4.2.1 总载分析

对转换前后的数据进行总力和总矩(相对飞机对称面的弯矩)比较，结果及误差分析如表1所示，可以看出：从飞机总体受载角度分析，与气动力载荷相比，转换后的载荷误差较小，均在3%以内。

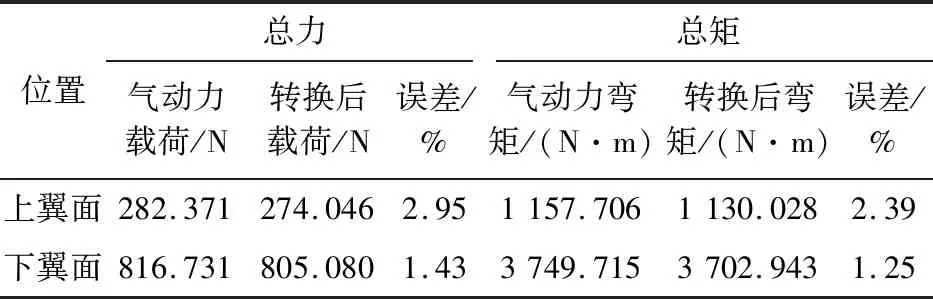
表1 载荷转换前后的总载对比Table 1 Total load comparison before and after load conversion

4.2.2 展向分布剪力、弯矩分析

对转换后的结点载荷沿展向积分，分别得到翼载的剪力、弯矩沿展向的分布，如图7所示。

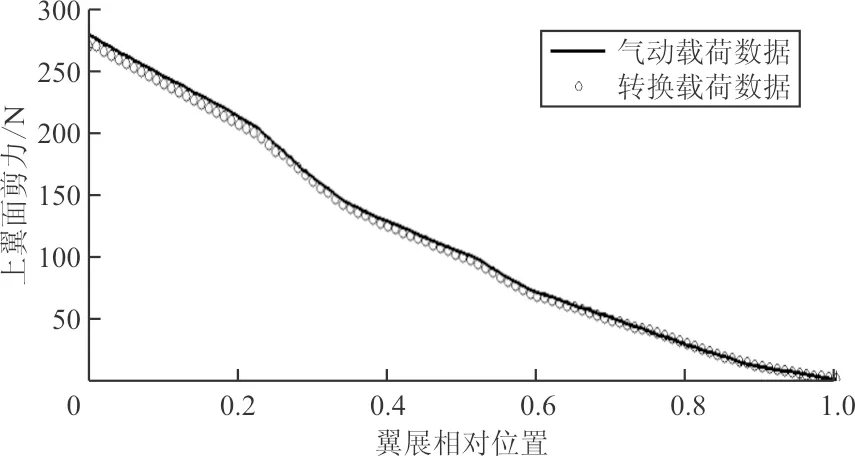
(a)上翼面剪力沿展向的分布

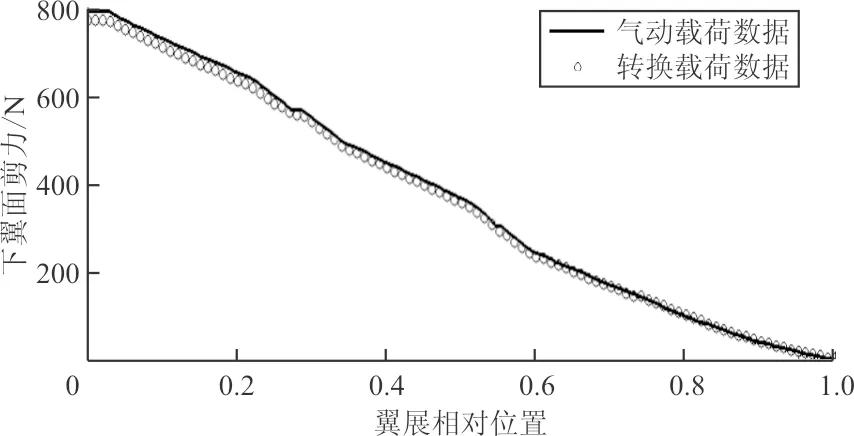
(b)下翼面剪力沿展向的分布

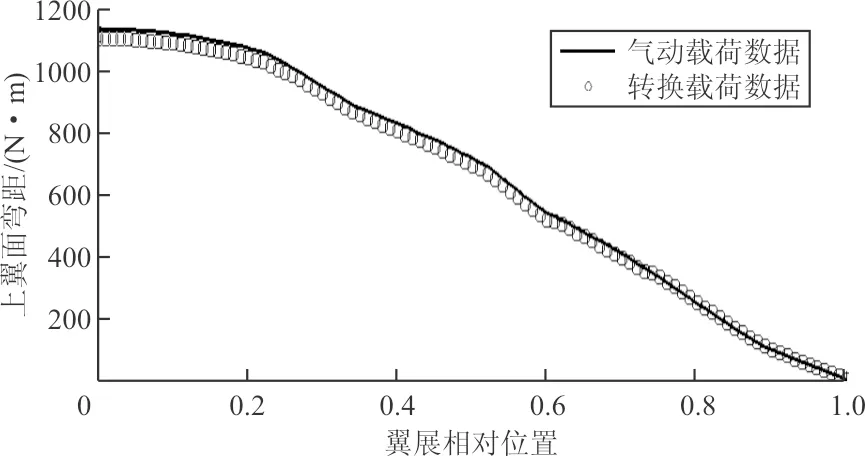
(c)上翼面弯矩沿展向的分布

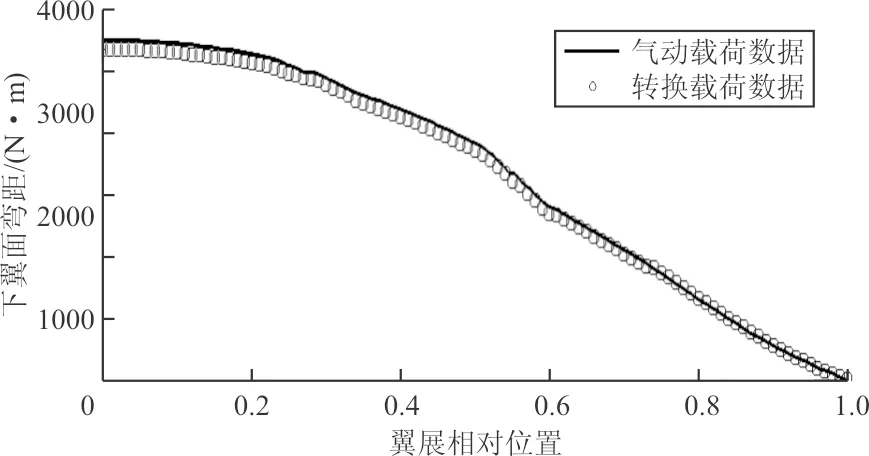
(d)下翼面弯矩沿展向的分布图7 转换前后展向截面剪力及弯矩对比图Fig.7 Contrast diagram of shear force and bending moment of spread section before and after conversion

从图7可以看出：分布载荷数据与气动数据吻合较好，由于误差累积，在翼尖处(横轴最大)误差最小，翼根处(横轴为零)误差最大，翼根处的剪力、力矩与翼面上总力和总矩相等，该处载荷误差如表1所示。

4.3 算例分析总结

通过简单算例及工程算例的载荷分析，转换后的结点载荷与气动载荷对比误差较小。通过本文所提出的方法得到的离散化载荷，能够真实地反映实际载荷分布，且程序实现简单，效率较高，无人为误差的引入，可用于工程计算。

5 误差分析

气动载荷是连续变化分布的，上述方法将其处理为微元上的均布载荷，在相邻微元边界处是不连续的，这将产生计算误差，文献[9]和文献[13]提出的方法其目的就是消除该误差。实践证明，在飞机设计的大多数情况，采用本文的算法进行分布载荷的离散化，其误差在可接受范围内。

6 结 论

(1)气动力、惯性力等以网点列阵形式提供的载荷数据，根据薄板单元集中力移置公式按单元移置到结点上；均布和线性分布的载荷，根据薄板单元面力移置公式按单元移置到结点上。

(2)在分布载荷作用区域内部的单元，结点载荷的力矩分量总和为零，可以忽略不计，但在分布载荷作用区域的边界处则不能忽略。

(3)本文所提方法实现的载荷转换，程序实现简单，效率较高，无人为误差的引入。系统误差在可接受范围内。