在思维的演绎中，培养学生的理性思维能力

彭晓金

物理学家狄拉克由一个正实数有正负一对平方根的引导，开启了粒子和反粒子、物质和反物质的研究，从而使人们发现了反粒子的存在。1937年，埃托雷。马约拉纳发表论文假想：存在一种费粒子，它的反粒子就是它本身。这与数学中零的相反数就是其本身是何等的相像。而在80年后，即2017年，由物理学家张首晟及其团队提出成功发现了这种费粒子，并称其为“天使粒子”。这使得人类对现有世界的认知，即世界不完全是正反对立的，有阴不一定有阳；同时，这一发现还具有更加现实的意义就是：在固体中实现拓扑量子计算将成为可能。

又比如，张首晟将欧拉公式V－E+F＝2在拓扑空间变为V－E+F＝X（P），其中X（P）叫做多面体中的欧拉示性数，是拓扑不变量。在平面上X（P）＝1为出发点，开创了拓扑绝缘体这个全新领域。他的这理论和实践将为信息技术带来革命性的发展。

这些事例都说明，良好的理性思维是人们原创性进行科学探索的源泉和动力。

我们也知道数学是思维的体操，正如瑞士教育家裴斯泰洛齐说：“教学的主要任务不是积累知识，而是发展思维。”，所以在平时的课堂教学中，能促进学生理性思维的发展是是多么的重要，这也正是数学课堂教学的灵魂所在。下面就课堂教学中如何培养学生理性思维谈谈具体做法。

一、在结构的变化中，培养学生理性思维的深刻性

一个人指思维过程所达到的认识深度，是思维活动的抽象程度和逻辑水平，它对发现问题和解决问题有十分重要的作用。

事例1.我们将勾股定理c2＝a2+b2作以下两个方面的结构性变化：

（1）c2＝a2+b2⇒2c2＝2（a2+b2），其几何结构为：

那么，就可引发一个原发性问题：平行四边形的对角线的平方和等于四边的平方和。

接下来，让学生用已学的知识去探究命题的真伪。当然，学生利用余弦定理或平面向量的基础知识都不难发现命题的正确性。

（2）c2＝a2+b2⇒c·c＝a·a+b·b，其几何结构为：

那么，可引发一个原发性问题：AC·BD ＝AD·BC+AB·CD。

接下来探索证明这个问题的方法。当然，大家知道这是著名的托勒密定理。

教学中，通过这样的结构变化，可将问题更加具有一般性，同时也培养了学生发现问题及解决问题的理性思维能力。

二、在维度的变化，培养学生思维的多样性和灵活性性

我们知道一个人在认识问题中，如果有维度的高低和层次的多少的变化，将思维独创性形成和思维创新行形成的重要环节，也是思考问题和解决问题时的方式方法灵活性的重要组成。

事例2.在平面四边形ABCD中（如下图），结论：cosθ ＝

是否正确？

证明：由余弦定理有：

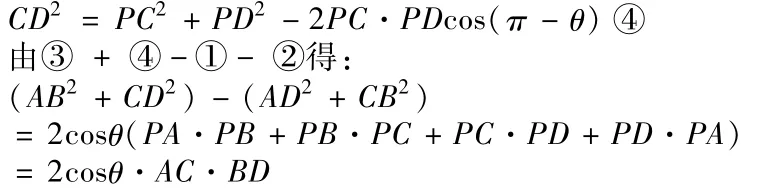
接下来，我们提出对空间四边形ABCD（A，B，C，D四点不共面），如下图，结论还成立吗？如果成立，显然就得到求异面直线AB，CD所成角θ的一个方法。

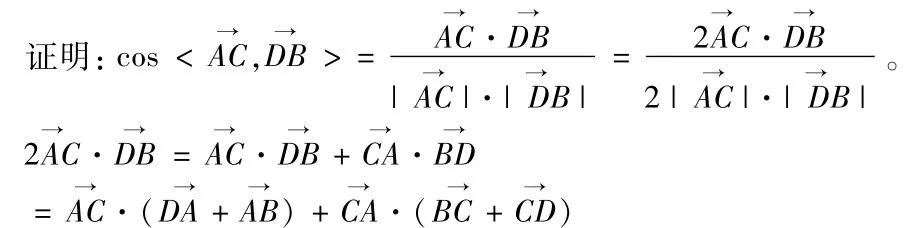
教学中通过这样的维度变化，可独创性的发现新问题，并在解决问题的过程中，提升学生的理性思维能力。

三、在从特殊到一般的变化中，培养学生思维的广泛性和普遍性

从特殊到一般是人们认识自然和探索自然常用的方法。如果我们在教学中能够经常引导学生进行这种有益的思维活动，对学生的思维的广泛性和普遍性一定有积极地提高，使得学生具有更开阔思路和全面地分析问题的能力，去多方面的思考问题和研究问题，从而更好的去探索大道至简的客观规律。

事例3已知点A（－2，0），点B在圆x2+y2＝1上运动，以AB为边向外作正三角形ABP（如下图），求点P的轨迹方程。

解：设P（x，y）是所求轨迹上的任意一点，B（x0，y0），记向量对应复数z1＝（x0+2）+y0i，向量对应复数z2＝（x+2）+yi。

则由已知有：

将B（x0，y0）代入圆的方程x2+y2＝1得：0。

下面作三方面的变化：

（1）将圆x2+y2＝1变为椭圆、双曲线、抛物线，以至于可以变为任意的曲线f（x，y）＝0，上述思路和方法仍然适用。

（2）将AB与AP的夹角从600变化为任意角θ，上述思路和方法仍然适用。

在教学中，通过上述三方面的变化，最终将问题演绎成一个最具广泛性的问题，并通过多角度的变化过程，进一步提升了学生的理性思维能力。若能经常利用好的问题背景，并抓住可变化的题材，一定能使学生的理性思维得以更好的更全面的培养，使他们今后更有能力去进行原创性的科学探索和研究。