数形结合在数学中的应用
□王永超
本文主要对数形结合的主要内容和作用加以分析,通过实际考察与学习、观察发现,有很多学生对应用数形结合非常陌生,还有部分同学知道数形结合,但不知道什么样的题型适合用数形结合,所以在这里进行详细说明。数形结合不仅是一种技巧,更是借助数学的精确性来阐明图形图象的某些特性。本文介绍了一些数形结合在数学中的应用,通过对具体应用的分析,加深读者对数形结合的印象。
一、在函数中的应用
函数是高中数学的一大教学板块[2],函数知识的抽象性非常高,学生在理解和掌握过程中都会遇到一些问题。这时候用数形结合帮助学生,结合形象的图形来理解函数知识,学生就会非常轻松地理解,并且更快地理解题意。
例1,如下图函数y=f(x)和y=g(x)的图像所示:下列选项( ),最可能是函数y=g(x)·f(x)的图像。
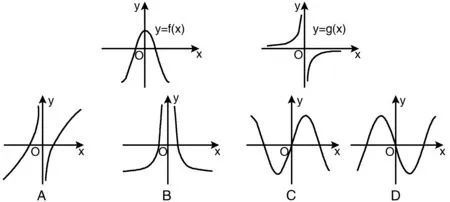
分析 ∵有图像可知函数y=g(x)·f(x)的定义域图像不经过点(0,0),
∴能够排除C,D两个选项
∵当x为非常小的正数时,f(x)>0且g(x)<0
(两数相乘“同号为正,异号为负”)
∴g(x)·f(x)<0
故选A选项。
二、在不等式中的应用
在解决不等式问题时,有很多方法,其中有一种方法就是利用数形结合,巧妙地处理无法直接计算的数量,将不等式所表达的抽象数量关系通过画图直观地表达出来,从而使原问题简单化。
例2,对不等式|x+a|+|x|<2求解(其中a为实参数)。
解 把原不等式变形为|x+a|<2-|x|
在坐标片面上作函数y=|x+a|,y=2-|x|的图像,前者是以(-a,0)为端点,斜率为±1的向上的两组平行射线;后者是以(0,2)为端点,斜率为±1的向下的两条射线(如图1所示)。

图1
设A(xA,yA),B(xB,yB)分别为上述两函数图像的交点,且xA>xB容易求得
从函数的图像可知,当a≤2或a≥2时,原不等式无解;
当-2 线性规划在数学中扮演着重要的角色,这里对简单的线性规划问题进行讨论分析,可以从中非常清晰地看出数形结合的重要性。 解 如图将以下直线x-3y+2=0,x+2y-8=0,x=1,在平面直角坐标系中表示出来.通过观察,图中的阴影部分符合题意,并且原点(0,0)不属于图中的阴影部分,只有当x=0,y=0时,z=x+y=0,即点(0,0)在直线l0;x+y=0上。作一条平行l0的直线l:x+y=s,s∈R,由图2可知,当l在l0的右上方时,点(x,y)满足题意,s随直线l往右而变大。 图2 由图象可知, 当直线l通过点A(4,2)时,此时对应的s最大, 当直线l通过点B(1,1)时,此时对应的s最小, 所以,zmax=4+2=6,zmin=1+1=2 此题完全是利用图象求解,通过画函数图象确定所选区域,再根据目标函数的图象找到最大值。 在处理几何问题的时候,常常利用数形结合去处理有关问题[3],钻研点、线、曲线的种种联系以及相关性质,使二者紧密结合起来,让数形结合的优势得以充分体现,从而使问题得到合理的解决。 图3 b2x2+(b2+5)y2=b2(b2+5), 联立直线与椭圆方程消去y得 解决此类问题时要充分利用图形和平面直角坐标系,使二者紧密结合起来,让数形结合的优势得以充分体现,从而使问题简单化,并得到合理解决。 概率在生活中很常用,在大学的概率论中也学习很多关于数形结合的知识,下面来看一下概率论中是如何实现数形结合的。 例5,甲乙两人相互商定在下午6时到7时之间在该地方见面,并约定先到达的人应等待后到达的人20min,超过时间即可先行离去.求两人能见面的概率[5]。 解 用x表示甲,用y表示乙两人到达约会地点的时间(以min为单位),在平面上建立xOy直角坐标系(如图4所示)。 图4 根据题意,先画出图形,再根据图形的几何意义找到对应的点以及函数,最后找到所求概率。本题的意义所在就是给出一个范围,根据对应的范围内求出想要的数的概率,也用图象清晰地表明计算结果。 本文通过对数形结合的了解,简述了一些数形结合的运用方法,进一步了解了数形结合在数学中的地位及其重要性。总之,要充分挖掘有意义的内容,将数形结合渗透于具体的问题中,正确运用数形结合解决问题带来了很多的方便,同时数形结合有利于提高思维的深刻性,让思维更开阔,为以后其他方面的学习奠定基础。数形结合与学习休戚相关,希望更多的人能重视数形结合[6]。三、在线性规划中的应用
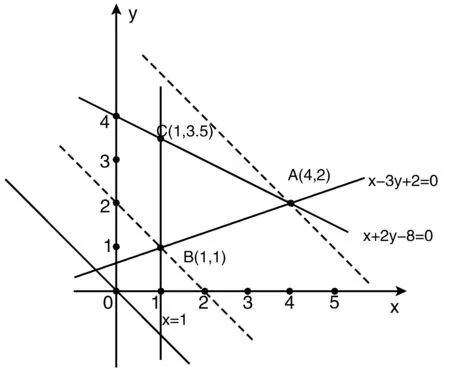
四、在几何问题中的应用
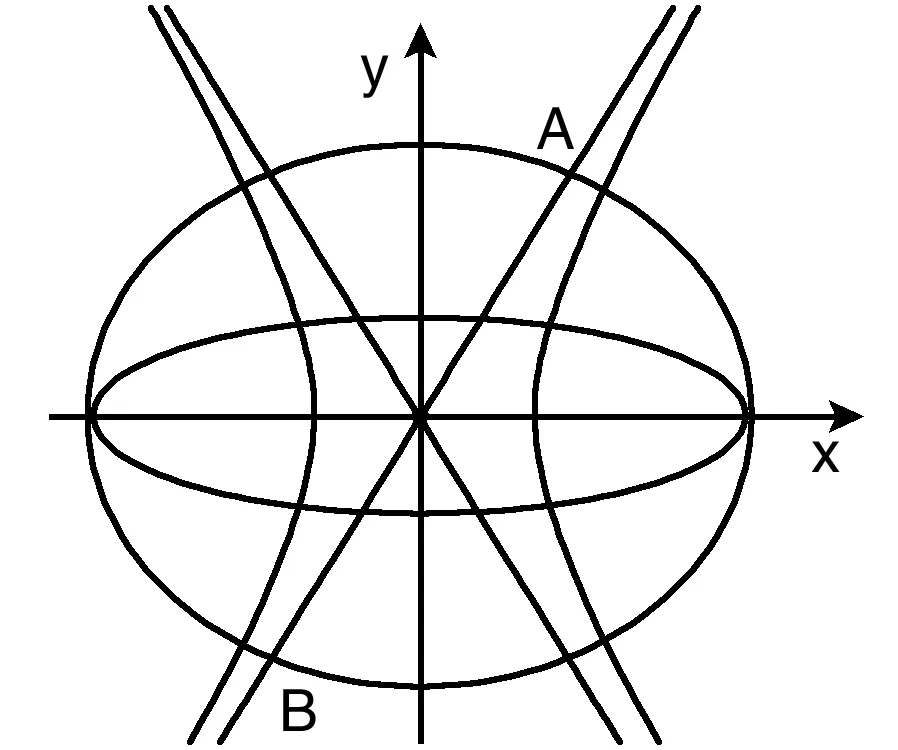

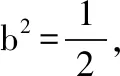
五、在概率论中的应用
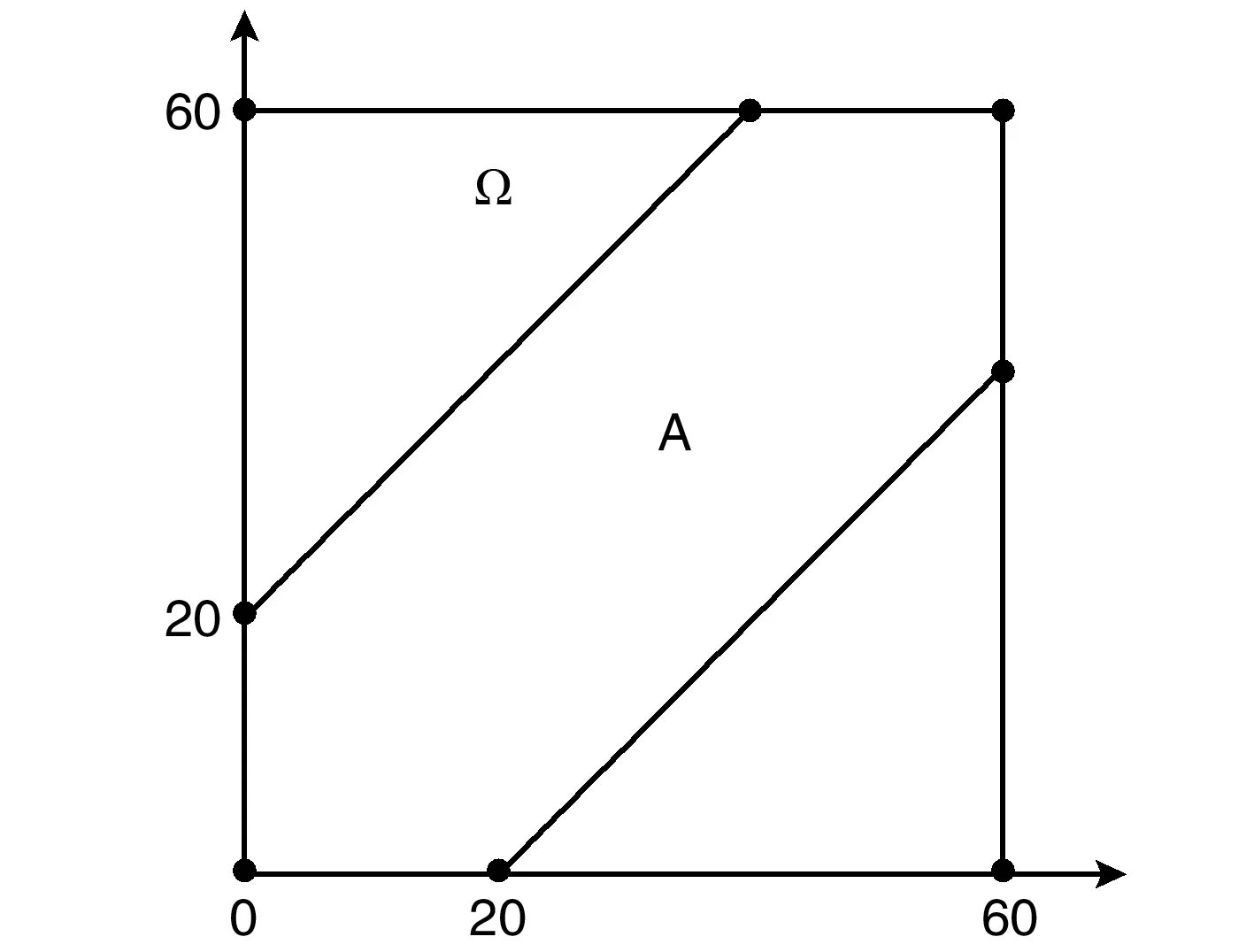
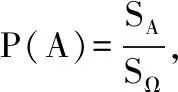
六、结语

