不同水位下滑坡渐进破坏稳定性分析

吴向东 张凌晨 卢应发

(1.湖北工业大学 土木建筑与环境学院，武汉 430068；2.中煤三建机电安装工程有限责任公司，安徽 宿州

234000)

中国是多山的国家，滑坡灾害每年造成经济损失两百多亿元.地质灾害实例表明：地震、降雨和开挖等是发生滑坡、泥石流的主要诱因.滑坡灾害经历起裂、局部破坏、直至整体破坏过程，部分演化为泥石流等特征，对地质灾害进行研究，并实施预测预报是非常必要的.边坡工程是一个古老的研究课题，众多学者对其进行了广泛研究，在假设滑体为刚体，破坏面均处于临界应力状态下，提出了不平衡推力法、瑞典圆弧法、简化Bishop法、Janbu法等，随着数值计算的发展，监凯维奇(Zienkiewicz O.C.)提出了有限元强度折减法等[1-6]，并应用于边坡极限稳定性分析.文献[7-9] 提出：针对沿滑面未破坏区进行强度折减，从而获得稳定系数；和针对滑面破坏区进行强度折减，并使临界状态一步一步向前移动，从而获得临界状态在不同位置时的稳定系数，两种部分强度折减法.

随着人们对自然物质认识的提高，针对传统强度折减法，文献[7-9] 提出的部分强度折减法的临界状态点是逐渐前移的，且此法分别对未破坏和已破坏的区域的强度进行了折减；文献[9-11] 在研究了岩土体行为的不同特征后，对其采用了Ⅰ、Ⅱ、Ⅲ型的特性进行分类，其中由试验机所产生的行为归属于Ⅱ型.提出了一种其参数具有清晰物理含义的剪应力模型，来描述整个过程中材料的变化.简要说明了推移式及牵引式滑坡产生滑移的原因、类别和界定准则[8，12-15]，沿破坏面将滑体按照稳定区、欠稳定区、临界状态及不稳定区的标准进行分类，分为阻滑区及驱动下滑区，法向应力在整个滑动面上都是连续分布的，而驱动下滑区的下滑应力与摩阻应力非连续，从而产生的位移也非连续，根据临界状态的滑坡特性，由不连续的应力及位移提出滑面边界的数值分析方法，从而给出了滑面非连续应力、应变状态及临界状态问题的求解方法.针对滑坡破坏过程的描述，在考察了其变形破坏原理的基础上，提出了以下5种描述法：综合下滑力-抗滑力法、综合位移法、主推(或拉)力法、拉破坏法以及富余位移法[8，12-14].对不平衡推力法等方法进行研究后，发现对于边坡渐进破坏过程的描述不适合用理想弹塑性模型[14]，这些方法在牵引式边坡稳定性的评估中不能较好适用，故定义了经验不平衡拉力法[16-17].对于边坡破坏形式的可能模式，基于满足摩尔库伦准则材料的应力主轴发生偏转，建立了破坏角转动法[18].由于传统计算方法采用的模型为理想弹塑性，当剪应力达到临界剪应力时，剪应变大小难以确定，而理想弹塑性模型不能描述材料软化特征等缺点，致使计算变形与实测变形不一致；另外传统条分法仅仅考虑力的传递，对峰值强度进行折减，其严密性和真实性低.本文运用渐进破坏理论，以改进的传统条分法对卡子湾滑坡进行了分析.

1 渐进破坏理论

1.1 力分布特征

按照文献[14-17] ，边坡在渐进变形破坏过程中，沿滑面的力来自于滑体，即滑面单元的上面来自于滑体的下滑应力(σuθ，σun，σuτ)，而滑面的力作用于滑床，即在滑面单元的下面来自于滑床的反作用应力(σbθ，(如图1所示)，从各点应力状态可得，推移式滑坡滑面的应力状态为，后缘抗滑应力较下滑应力小，其抗滑应力与下滑应力相等的位置处于临界应力状态，且此处抗滑力为最大值，前缘的抗滑应力比临界状态值小，但与下滑应力相等.

图1 滑面单元示意图

二维推移式滑坡的坡面受到滑体产生的下滑力(Pi)及压力(Ni)和滑床对其的反压力(Pi)及摩阻力(Ni)，如图2所示.滑面临界状态点上部的摩阻力小于下滑力，但反压力等于压力，而临界状态点下部的摩阻力等于下滑力且反压力等于压力，仅有临界状态点的摩阻力为临界值.由力的分布可以看出，力的平衡并不存在于整个滑体的渐进变形破坏过程，但沿滑面在破坏后区的摩阻力值比下滑力值小，每一点处的反压力等于压力值，临界状态点的下滑力值与摩阻力最大值相等；且在滑面破坏后区，沿滑面的位移值大于滑床的位移值.

图2 推移式滑坡沿整个滑面力分布特征

1.2 稳定性描述

根据文献[7-10] ，对于推移(或牵引)式滑坡，从后(或前)缘至临界状态产生驱动下滑(或牵引)力，从临界状态至前(或后)缘，存在剩余摩阻力，由于该剩余摩阻力阻止滑坡继续发生破坏，只有在临界状态存在力平衡.针对临界状态的准确定义为：当驱动应力达到材料的最大强度时，该状态为临界状态；亦即：临界状态并不一定对应于材料的峰值应力状态.如：当滑坡发生整体破坏，运动一段距离后处于整体稳定状态，此时的临界状态对应的应力可能为破坏后区某应力状态，即临界状态有时与临界应力状态一致，有时并不一致.

1.2.1 点描述

在滑坡应力、应变变化特征的基础上，针对滑面上某点的稳定系数定义为：

对于一点而言，定义应力稳定系数(Fσs)为：材料的极限应力除以所承受的应力，当该值大于1时，表示该点稳定，小于1时，表示该点已发生破坏.另外定义应变稳定系数(Fεs)为：材料的极限应变除以所承受的应变，当该值大于1时，表示该点稳定，小于1时，表示该点已发生破坏.以上述定义来确定滑坡每点的稳定状态.

1.2.2 滑坡整体稳定性描述

边坡整体稳定性分析一直是科研工作者研究的课题，基于上述分析，定义边坡整体稳定系数如下：

1)综合下滑力-抗滑力稳定系数(CSRM)

利用现行方法可以计算沿可能破坏面的现状应力场(如图3所示)虚线ABDEC表征可能的破坏面)，计算在X、Y和Z方向的滑动力矢量和为：

其中：Pxs，Pys，Pzs分别为滑坡现状沿可能滑动面在X、Y和Z方向的现状滑动力矢量和，Ω为积分区总面积，Ωf为破坏区面积，ΩR为非破坏区面积.

图3 破坏区分布和在X、Y和Z轴方向的投影

Pxs，Pys，Pzs的合矢量(Ps)为：

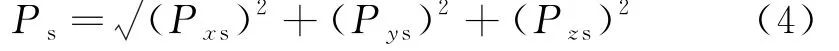
合矢量(Ps)与坐标轴X、Y和Z轴方向余弦为αs，βs，γs.

在可能的破坏模式下，计算沿可能破坏面的抗滑摩阻应力(σp，bn，σp，bθ，σp，bτ)分布，在X、Y和Z方向的抗滑力分别为：

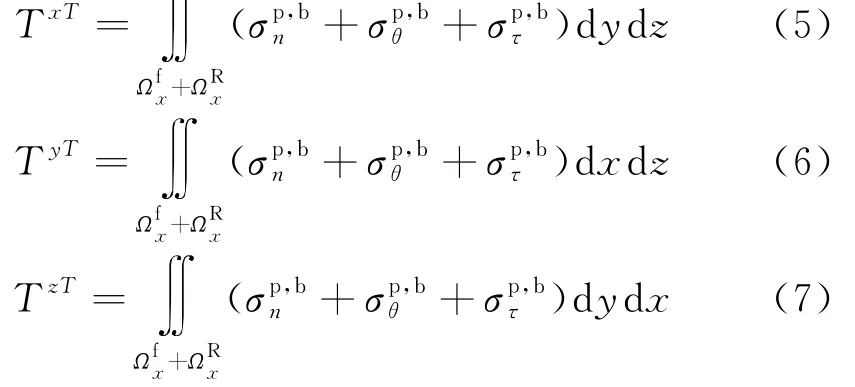
其中：TxT，TyT，TzT分别为在在X、Y和Z方向的抗滑力.

TxT，TyT，TzT的合矢量(TT)为：

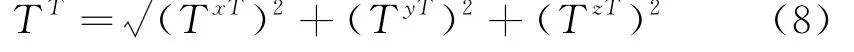
抗滑力合矢量与坐标轴X、Y和Z轴方向余弦分别为αT，βT，γT.

滑动力矢量和(Ps)与抗滑力矢量和(TT)的夹角(φc)为(如图4所示).

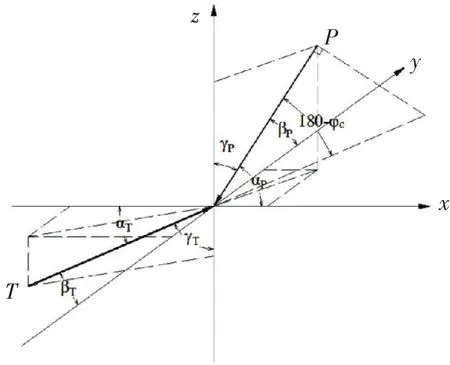
图4 在可能破坏模式下滑动力与抗滑力矢量和关系图

在X轴方向的稳定系数定义为：

在Y轴方向的稳定系数定义为：

在Z轴方向的稳定系数定义为：

在滑动力方向的稳定系数定义为：

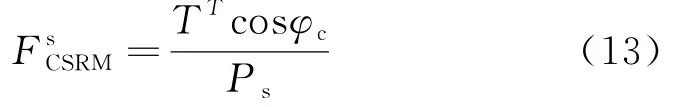
2)主推(或拉)力法稳定系数(MTM或MPM)

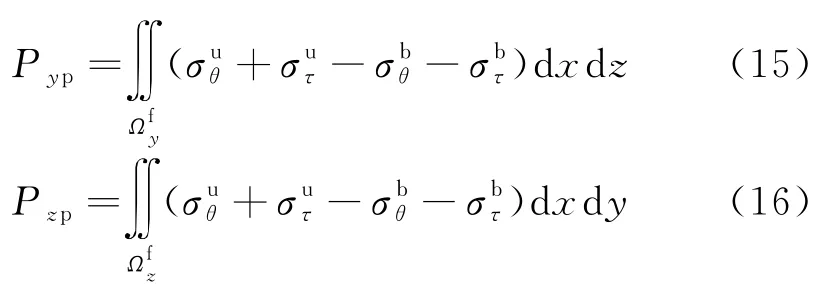
剩余下滑力(Pxp，Pyp，Pzp)的矢量和(Pp)为：

剩余下滑力矢量和(Pp)与X、Y和Z的方向余弦分别为αp，βp，γp.

在现状条件下，可以计算从临界状态到前缘的剩余摩阻力，其值为在可能破坏状态下滑面摩阻应力与现状摩阻应力之差 在 未破坏区域的积分，在X、Y和Z轴方向的表达式分别为：

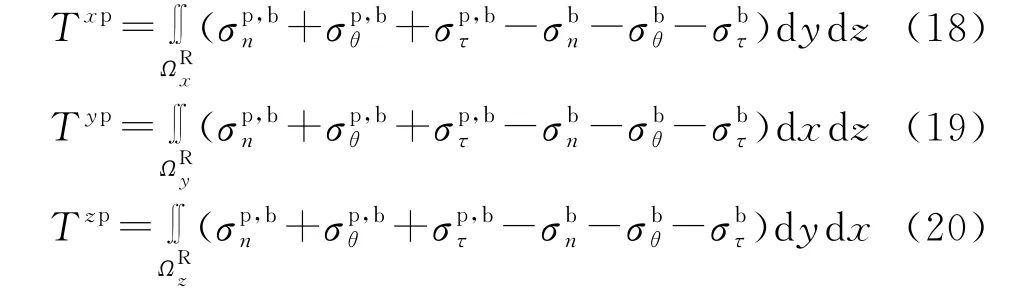
剩余摩阻力(Txp，Typ，Tzp)的矢量和(Tp)为：

剩余摩阻力矢量和(Tp)与坐标轴X、Y和Z轴方向余弦分别为αr，βr，γr.

剩余摩阻力矢量和(Tp)与剩余下滑力矢量和(Pp)的夹角(αm)为：

综上所述，城市化进程为建筑行业发展提供良好契机的同时也为工程项目管理带来了巨大的挑战。作为建筑管理的重要方面，进度管理直接关系着工程质量和成本，因此应该加强进度管理模式的改进创新，促进行业持续健康发展。

在X轴方向的主推力稳定系数定义为：

在Y轴方向的主推力稳定系数定义为：

在Z轴方向的主推力稳定系数定义为：

在主滑方向的主推力稳定系数定义为：

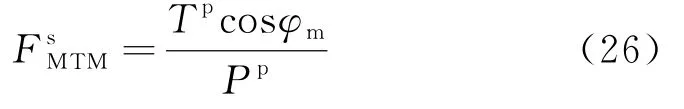
相似于推移式滑坡，利用主拉力法评价牵引式滑坡稳定性，其计算方法与主推力法一致，只是剩余拉力产生于滑坡前缘至临界状态，而剩余阻力产生于临界状态至后缘，以此分别定义：在X、Y、Z轴和主拉力方向稳定系数

3)综合位移法稳定系数(CDM)

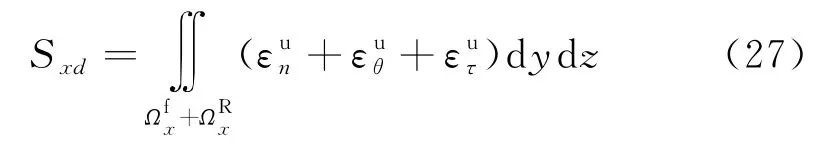
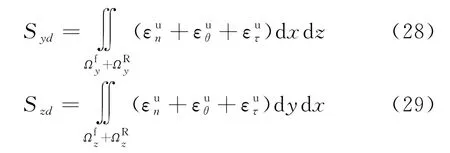
在X、Y和Z轴方向位移(Sxd，Syd，Szd)的矢量和(Sd)为：

位移矢量和(Sd)与坐标轴X、Y和Z轴方向余弦分别为αd，βd，γd.在分析可能破坏模式基础上，计算可能破坏模式的应变分布(εp，bn，εp，bθ，εp，bτ)和在坐标X、Y和Z轴方向的位移(Sxd，Syd，Szd)：

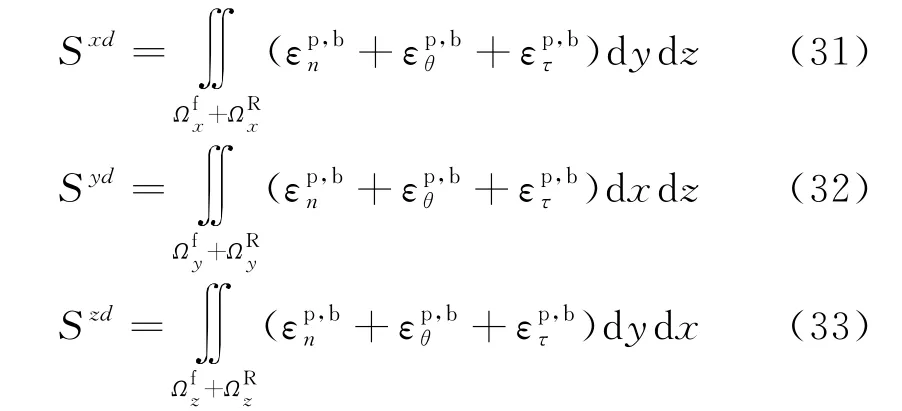
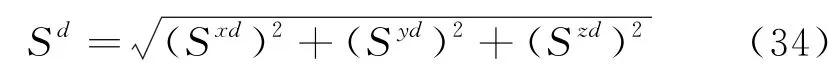
相应的位移矢量和(Sd)为：位移矢量和(Sd)与坐标轴X、Y和Z轴方向余弦分别为αd，βd，γd.两者矢量和(Sd与Sd)之间的夹角(φd)为：

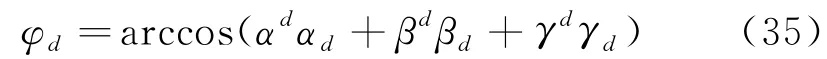
在X轴方向的综合位移稳定系数定义为：

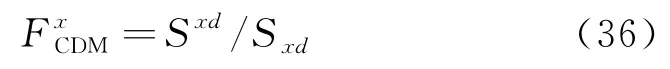
在Y轴方向的综合位移稳定系数定义为：

在Z轴方向的综合位移稳定系数定义为：

在主滑位移方向的综合位移稳定系数定义为：

4)富余位移法稳定系数(SDM)

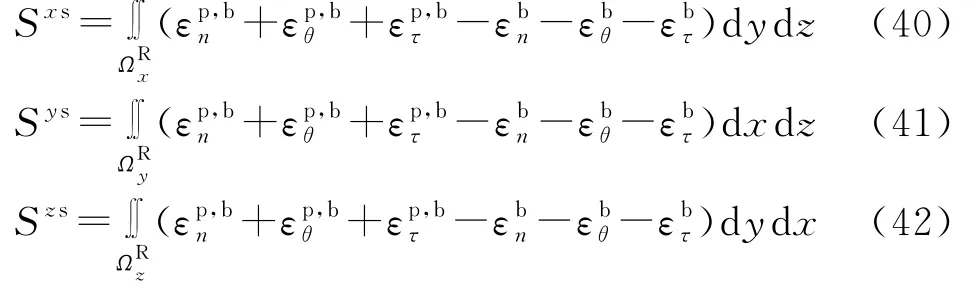
式中，Sxs，Sys，Szs为在X、Y和Z轴方向的富余位移.它的矢量和(Ss)为：

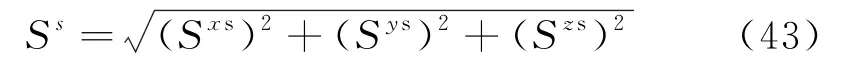
其矢量和与X、Y和Z轴方向余弦分别为αs，βs，γs.该矢量和与可能破坏位移矢量和(Sd)的夹角(φs)为：

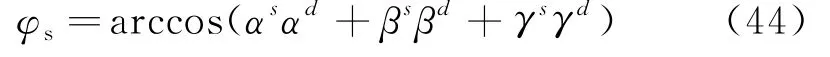
富余位移法在X轴方向的稳定系数为：

富余位移法在Y轴方向的稳定系数为：

富余位移法在Z轴方向的稳定系数为：

富余位移法在主滑移方向的稳定系数为：

1.3 全过程剪应力-应变本构模型

滑坡渐进破坏的特性决定了用于描述岩土体软化特点的本构模型的必要性，一种四参数的剪应力-应变方程表示为：

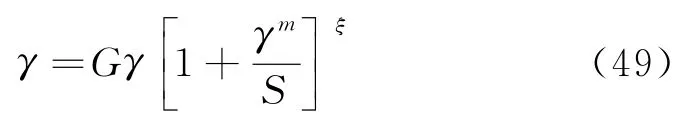
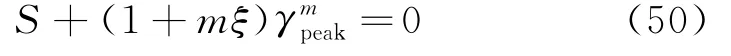
其中，γpeak为临界剪应力对应的剪应变，即临界应变.

不妨假设可由摩尔库伦准则确定临界剪应力τpeak(注：也可由其它相关准则确定)：

其中，C表示凝聚力；σn表示法向应力，二者单位均为 MPa、k Pa、Pa；φ表示滑面摩擦角.

可将临界剪应变γpeak假设为只由法向应力决定，且关系式如下：

其中，τ为剪应力(单位：MPa或k Pa或Pa)；γ为剪应变；G为初始剪切模量，与法向应力相关(单位：MPa或k Pa或Pa)；S、m、ξ均为法向应力决定的常数，无量刚.

若材料的行为具备软化特征，则满足：-1＜ξ≤0与1+mξ≠0.对于临界应变的关系式如下：

式中，ai，1，ai，2，ai，3为常系数.ai，1，ai，2单 位 为 MPa或k Pa或Pa，ai，3为无量纲系数.且：

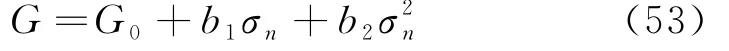
式中，G0为法向应力σn为零值的G值，b1，b2为常系数，单位为无量纲和1/MPa或1/kPa或1/Pa.

对于无量纲参数ξ，可以表示为：

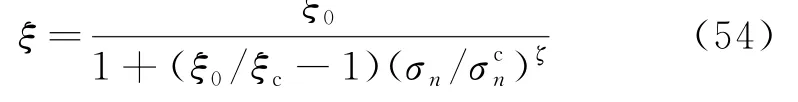
其中，ξ0表示法向应力(σn等于零时的ξ值，取-0.999 9)，ξc表示σn取时的ξ值，ζ表示常数；通过不同法向压力剪切试验获得的曲线可求得该式各参数.

模型参数的物理意义：对于传统的摩尔库伦准则和剪切模量参数的物理意义没有必要再次说明，但是对于方程(54)，ξ物理意义为描述材料在不同法向应力作用下的软化程度.而系数m，S为联系峰值应力和临界应变的相互关系，它们是过度参数.这个模型相对传统模型而言，只是实施全过程试验，各种参数可以试验决定，且具有明确的物理意义.

1.4 部分强度折减法

本文基于传统条分法提出部分强度折减法，按照传统条分法(以不平衡推力法为例)的基本思想，条块划分如图5所示.考虑水压力的计算公式为：

图5 第i条块受力图

正压力Ni为：

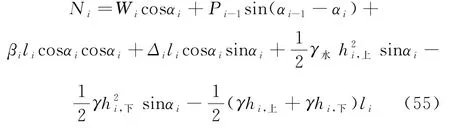
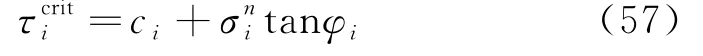
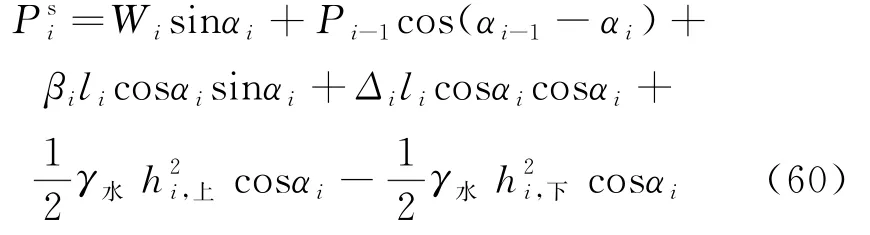
剩余下滑力Pi为：

其中，Wi表示第i块重量；βi表示垂直于水平的地表均布荷载；Δi表示沿水平方向均布荷载；li表示条块底边长；αi表示水平和条块底边成的夹角；F为稳定系数为法向应力；γ水表示水比重；hi，下表示条块左边水高度；hi，上为条块右边水高度，ψi为分布荷载与水平的夹角.

传统条分法将公式(55)～(61)进行多次迭代计算，直至最后一个条块(如图6中第n条块)的剩余下滑力等于零，从而获得稳定系数F.部分强度折减法的思想为：在给定的凝聚力(ci)和摩擦角(φi)下，首先计算在F=1时条块对应位置，如果第m的条块对应于F=1，则依次计算1～(m+1)，1～(m+2)直至1～(n-1)条块的稳定系数，最后条块的稳定系数对应于1～n条块，其对应的物理意义为：现状临界状态为第m条块，随着时间的推移，变形的增加，临界状态从第m条块移动至第n条块，滑坡整体从部分稳定状态变化为整体处于破坏状态.

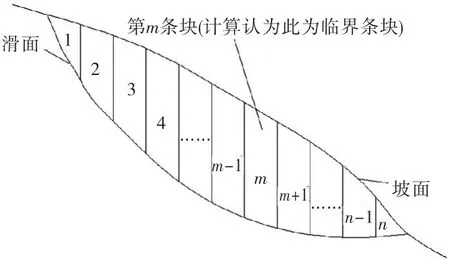
图6 边坡稳定分析条块划分图

1.5 新条块法

新条块法将克服传统条分法的一些缺点，以剩余推力法为例，对考虑水压力的新条块法作如下介绍.

基本假设：

1)假设条块具有足够的变形能力，条块以竖向一定间隔加以划分；

2)后面条块对前面条块的作用力平行于后面条块的底边，作用力位于前面条块的中心；

3)不考虑条块转动；

4)条块底边抗滑应力满足全过程剪应力-应变本构方程；

5)第i与i+1条块的应变满足平行和垂直底边方向上剪应变的矢量和(如图7所示)，其相连条块剪应变具有如下特点：

亦即，

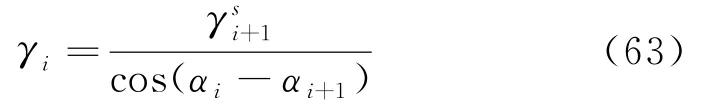
基于以上各假设，得到条块力-位移法计算公式如下：

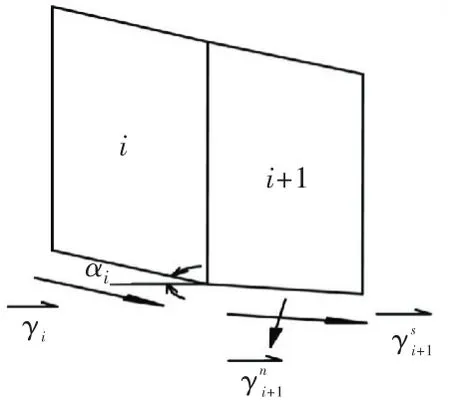
图7 相连条块的应变关系

第i条块：正压力Ni同式(55)，正应力σni同式(56).

摩阻应力τi为：

摩阻力Ti为：

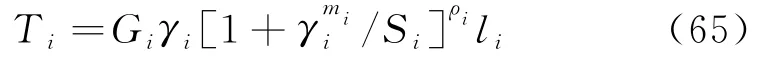
剩余下滑力Pi为：

式中，γi为第i条块底边剪应变.

2 实 例

以三峡库区卡子湾滑坡为实例，探讨滑坡渐进破坏理论的应用.

2.1 滑坡概况

卡子湾滑坡位于秭归县，地理位置(X：3 432 550，Y：37 471 500)，经度：110°41'37″，纬度：31°0'48″；该滑坡位于归州河左岸，距河口1.9 km，距三峡大坝44 km.其基本特征为：后缘高程720 m，前缘高程85 m，滑坡坡向2960，坡长1 270 m，坡高635 m，坡度15°～40°(如图8所示).

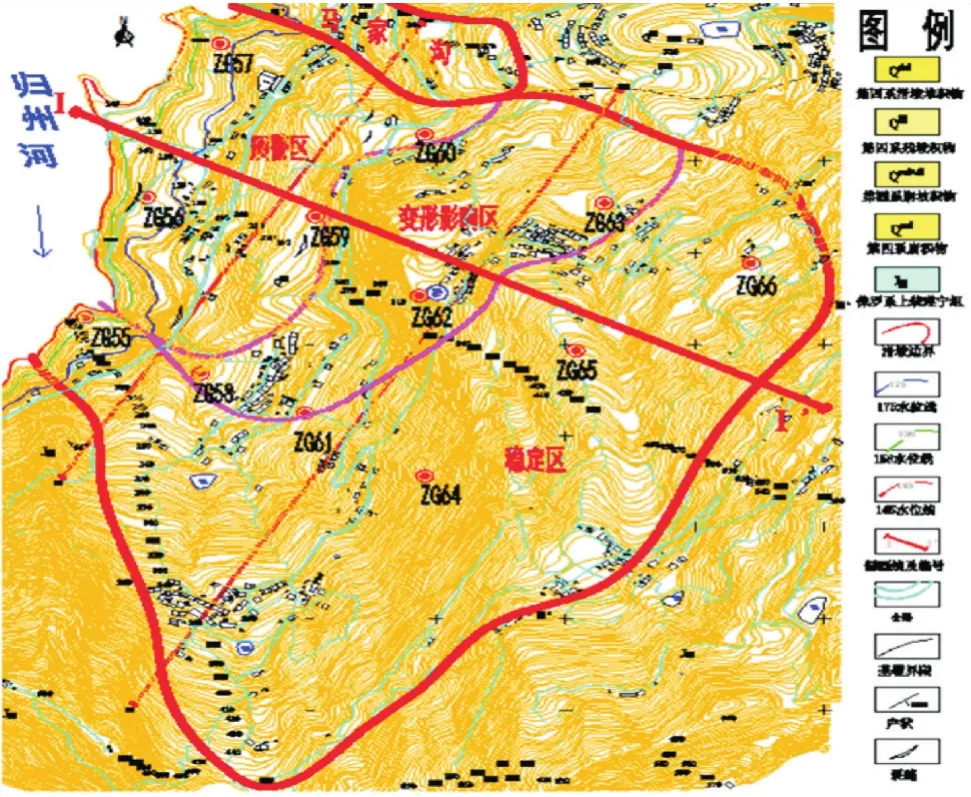
图8 卡子湾滑坡平面图

第四系分布于该滑坡范围内，且形成堆积物，由含碎块石粉质粘土组成，滑坡内坡脚陡坡处块石含量增多，中后部块石含量减少，前部可见孤石，粒径多在0.4～1.0 m，大者1.0 m以上.地层岩性为侏罗系上统遂宁组砂岩与泥岩互层地层，紫红色粉砂质泥岩、粉砂岩与长石砂岩，滑坡东北向出露基岩产状为280°～320°∠26°～39°，裂隙产状180°∠82°，240～250°∠46～79°，泥质充填裂隙；滑坡南西侧向基岩出露，产状为65°∠66°，该滑坡为顺向坡.

归州河为卡子湾滑坡前缘临空面；左侧边界走向：340°、长度：1 000 m；边界内地形坡度较缓，坡度约20°；下部以冲沟为界，上部以陡缓交接处为界；右侧边界走向：210°、长度：1 000 m；以冲沟为界，沟两侧坡面较陡.滑坡组成岩石为砂岩与泥岩岩层，泥岩经水浸泡易软化形成软弱层.

卡子湾滑坡的变形主要体现在滑坡体内部，这是由于卡子湾滑坡处于归州河左岸自然滑坡上，为顺向坡，滑坡组成岩石为砂岩与泥岩岩层，滑带天然形成.另外雨水及库水渗入滑体增加了滑体土重量，降低了滑体的强度，引起滑体产生失稳变形.

2.2 计算分析

按平面图(图1)上I-I'剖面图可得条分法计算图如图9所示，滑坡滑体重度为20 k N/m3，条块划分、条块底边角度和长度如图9所示.

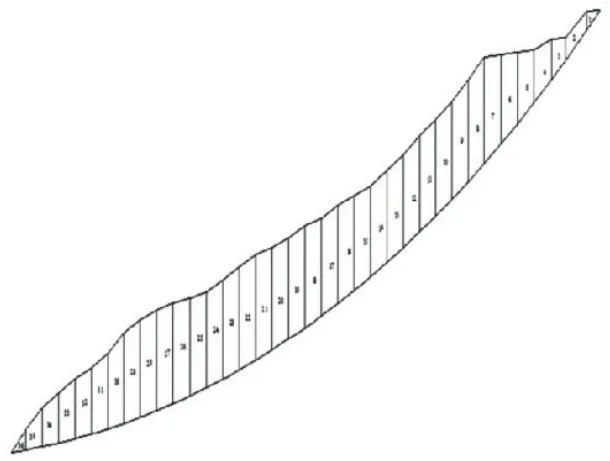
图9 卡子湾滑坡条块划分图

模型参数如下：凝聚力24 kPa，摩擦角φ=23°，剪切模量G=2 850 k Pa，ρi，0=-0.999 9，ρi，c=-0.51，k Pa，ai，1=2 000 k Pa，b1=50，b2=0 k Pa.

针对卡子湾滑坡，按照条分法划分条块如图9所示，按照传统临界状态法，根据文献[19] ，结合该滑坡渗流计算，在175 m水位下考虑20年一遇雨水(亦即滑体1/3饱水)条件下，其稳定系数为1.165，处于基本稳定状态，破坏面积比为0.61；按照本文提出的临界状态部分强度折减法，当稳定系数等于1时，其临界状态为26号条块，当临界状态条块向前移动时，其部分强度折减法所获得的稳定系数见表1.

表1 20年雨水作用下部分强度折减法稳定系数表

按上述渐进破坏理论，对卡子湾滑坡进行稳定性分析，其综合下滑力-抗滑力、主推力、综合位移和富余位移法等稳定系数见表2.

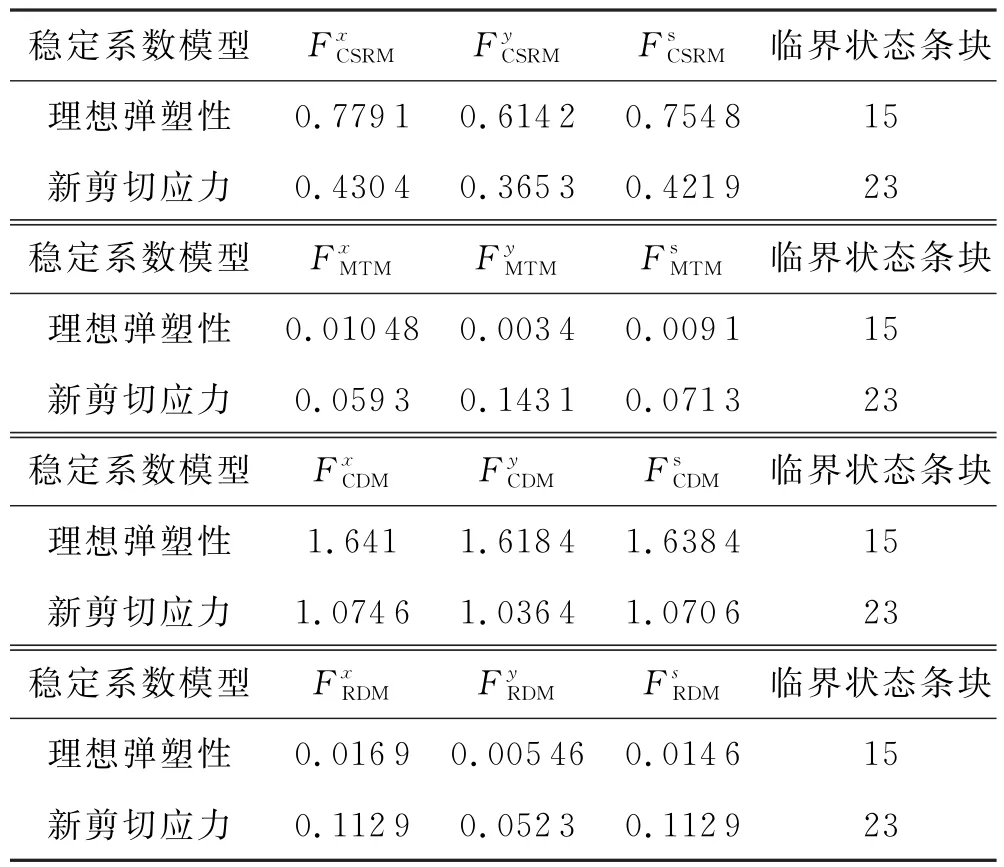
表2 20年雨水作用下渐进破坏稳定系数表

在175 m水位下考虑50年一遇雨水(亦即：滑体2/3饱水)条件下，其稳定系数为1.069，处于基本稳定状态，破坏面积比为0.65；按照本文提出的临界状态部分强度折减法，当稳定系数等于1时，其临界状态为30号条块，当临界状态条块向前移动时，其部分强度折减法所获得的稳定系数见表3.

表3 50年雨水作用下部分强度折减法稳定系数表

相对应的综合下滑力-抗滑力、主推力、综合位移和富余位移法等稳定系数见表4.

对以上由计算得到的稳定系数进行分析可得，用传统方法在175 m水位下，滑体按1/3饱和计算得到的稳定系数是1.165，长期以来此稳定系数让人们产生了“等于1是临界稳定状态，而0.165则为富余系数”的印象，在这种情况下，在临界状态单元为26条块时，将结果与渐进破坏主推力和富余位移法系数比较，它们在水平轴、竖直轴和主滑方向计算的富余系数分别为0.112 9，0.052 3，0.112 9；表明传统计算结果偏大.

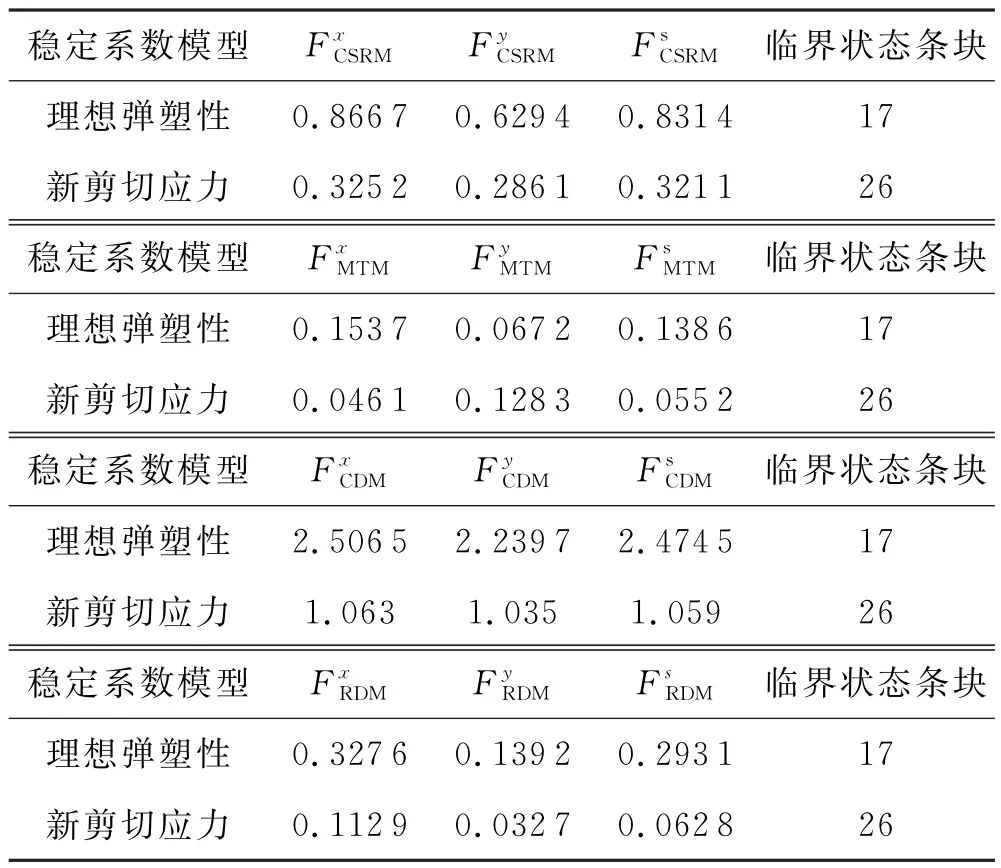
表4 50年雨水作用下渐进破坏稳定系数表

用传统方法在175 m水位下，滑体按2/3饱和计算得到的稳定系数是1.069，长期以来此稳定系数让人们产生了“等于1是临界稳定状态，而0.069则为富余系数”的印象，在这种情况下，在临界状态单元为30条块时，将结果与50年一遇的渐进破坏主推力和富余位移法系数比较，它们在水平轴、竖直轴和主滑方向计算的富余系数分别为0.041 9，0.032 7，0.0628.

从计算结果可知，传统临界计算的稳定系数比全新剪应力本构模型计算的值要大，产生这种结果的原因很显然是传统方法对抗滑力的折减造成了相应条块传递至下一条块的下滑力增大，由此下一条块的法向应力增大，导致相应的抗滑力增大，所以只有增大折减系数才能使最后的条块处于临界应力状态，这样算得的结果自然偏大.而用有明显物理意义的主推力与富余位移法所得结果与实际相符合.

3 结 论

本文基于滑坡渐进破坏理论，获得如下研究成果：

1)本文比较了两种水位条件下传统的强度折减法稳定系数、部分强度折减法稳定系数和渐进破坏稳定系数，结果表明50年一遇雨水稳定系数小于20年一遇雨水.并论证了部分强度折减法可以近似描述滑坡的渐进破坏过程.

2)本文证明了地质材料全过程力学行为可以用全过程剪应力-应变本构模型来进行描述，该模型可以描述岩土材料的力学行为特征.

3)基于全过程剪应力-应变本构模型的渐进破坏过程描述是部分强度折减法的深层描述，具体表现在：稳定系数随变形的变化而变化.

4)新的稳定系数随变形的增加，主推力法和富余位移法稳定性系数下降，到达临界状态时，稳定系数为0；而综合位移法的稳定系数为1；3种稳定系数可以较好描述滑坡的渐进破坏过程.