降解和压缩作用下垃圾土气体渗透率非线性定量表征模型研究

曾 刚 王 婧 胡 丹 马 骏

(1.湖北文理学院 土木工程与建筑学院，湖北 襄阳 441053；2.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，武汉 430071)

填埋气体虽具有温室效应高、易燃易爆的危害和风险，但它却是一种新型的清洁能源，可用来发电、供气或汽车燃料[1-3].填埋气体的收集利用一方面可以减少环境污染问题，另一方面可以变废为宝，创造可观的环境效益、社会效益和经济效益，和习近平总书记在十九大报告中强调要着力解决突出环境问题，加强固体废弃物和垃圾处置，推进绿色发展，构建市场导向的清洁生产产业和清洁能源产业极度吻合.

填埋气体的灾变控制与资源化利用具有重要的现实意义，也是环境岩土工程领域研究的热点课题之一[4-5].填埋气体迁移规律的定量化研究是填埋气体污染控制及资源化利用的重要理论基础[6].垃圾土的气体渗透特性是反映多孔介质自身传递流体能力的物理参数，是描述填埋气体在垃圾土中迁移路径的主要因素，是影响填埋气体迁移规律预测和收集导排的重要参数[7].系统掌握垃圾土的气体渗透特性，可为填埋气体迁移规律的合理预测提供理论依据，为科学而有效的收集利用填埋气体提供技术支持.

降解和压缩作用是垃圾土的气体渗透特性等工程性质改变的重要因素[8].因为垃圾堆体承受了上覆垃圾、日覆盖层及压实操作时的机械荷载，垃圾土在上述荷载作用下固体骨架结构因压缩而重新调整导致其孔隙结构发生改变；同时，垃圾填埋后在新填埋的垃圾或日覆盖层的封盖下，已填埋垃圾在很短时间内即进入厌氧环境，可降解的有机固相组分在降解作用下分解破碎成较小颗粒，垃圾土的孔隙结构在降解作用下也发生改变.因此，构建降解和压缩耦合作用下垃圾土气体渗透率非线性定量表征模型，定量分析垃圾堆体中气体渗透特性的演化规律显得尤为必要.彭绪亚等[9]自主研制了箱体导气试验装置，研究了压实密度和含水率对垃圾体渗透特性的影响，垃圾体渗透系数随压实密度的增加呈指数规律衰减.魏海云等[10]研制了垃圾土气体渗透试验装置，并开展了苏州市七子山垃圾填埋场现场垃圾试样气体渗透的室内试验，结果表明孔隙比、饱和度和组分均对气体渗透性均有显著的影响.Hossain等[11]开展了降解对垃圾土气体渗透特性影响的室内试验，结果表明降解作用会降低试样的气体渗透率，且在相同密度时随着降解的发生气体渗透率是以0.001 3 cm/s减小.Stoltz等[12]自主研制了生活垃圾土气体渗透试验装置，开展了法国某填埋场新鲜垃圾土试样在0～140 k Pa作用下的气体渗透性试验，结果表明渗透率的范围为10-10m2～10-14m2.易富等[13]采用自制的生活垃圾渗透率/孔隙度测试实验装置，探讨了上覆载荷对垃圾堆体渗透特性的变化规律，构建了固有渗透率与孔隙度之间的协同表征模型.曾刚等[14]研究表明垃圾土固有渗透率随着试样尺寸的增加而增加，变化幅度超过了一个数量级，且幂函数模型适用于新鲜垃圾和陈腐垃圾，K-C模型只适用于陈腐垃圾.施建勇等[15]研制了垃圾土的非饱和渗透试验仪，开展了气体压力和孔隙对垃圾土气体渗透系数影响的室内试验，研究发现渗透系数随渗透压力呈现非线性特性.对于垃圾堆体气体渗透性能的现场试验以及人工配样、填埋场钻孔取样的室内试验有较多的研究成果，但关于垃圾土气体渗透率定量表征模型方面的报道还较少，与此相关的研究工作还有待完善.本文的工作是基于垃圾土气体渗透率-孔隙度关系的幂函数模型和复合压缩模型，建立了考虑降解和压缩作用的垃圾土气体渗透率定量表征模型，分析了压缩系数、生化降解应变和生化降解速率常数等参数对气体渗透率定量表征模型的演化规律和影响机理.

1 降解和压缩作用下垃圾土气体渗透率非线性定量表征模型构建

针对垃圾土的气体渗透率随孔隙度动态变化的特点，建立垃圾土气体渗透率定量表征模型显得尤为必要.在已知初始气体渗透率和其他参数的情况下，通过模型可以得到任意时刻垃圾土的气体渗透率.模型建立的思路是基于表征气体渗透率、孔隙度的幂函数模型和表征垃圾土沉降变形的复合压缩模型，得到考虑降解和压缩作用的垃圾土气体渗透率定量表征模型.具体的建立过程如下.

Stoltz[16-17]提出了孔隙度的表达式为：

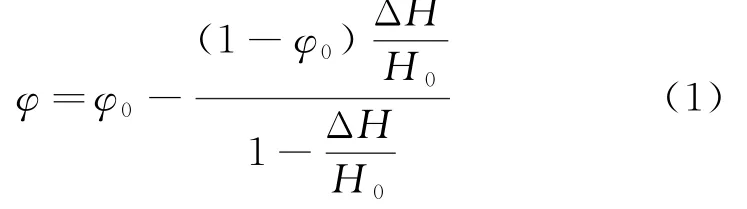
引入变形ε=ΔH/H0的表达式，可对式(1)进行如式(2)的变换.

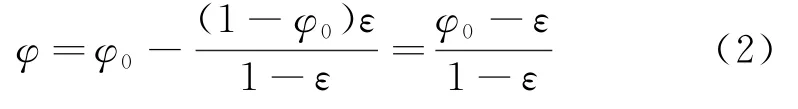
对式(2)进行变形，可得到任意时刻孔隙度和初始孔隙度的比值，见式(3)：

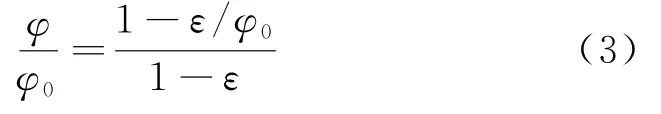
采用经典模型幂函数公式来表达气体渗透率和孔隙度的关系[16]，见式(4)：

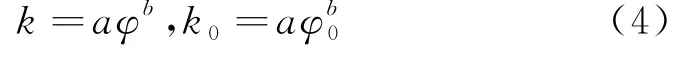
将式(3)代入到式(5)中，可获得气体渗透率的定量表征模型，见式(6)：

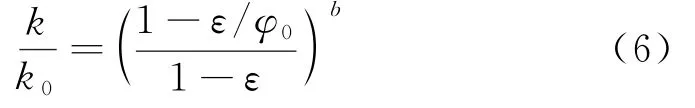
对式(4)进行变换，可得到式(5).

Marques等[18]提出垃圾土的复合压缩沉降模型，将垃圾土的沉降变形ε分为3部分来考虑，即和荷载相关的瞬时沉降、和时间相关的机械蠕变沉降，以及和时间相关的生物降解沉降，表达式为：

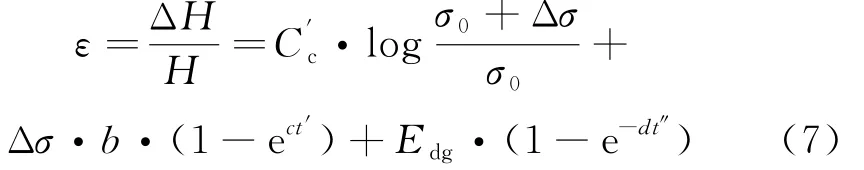
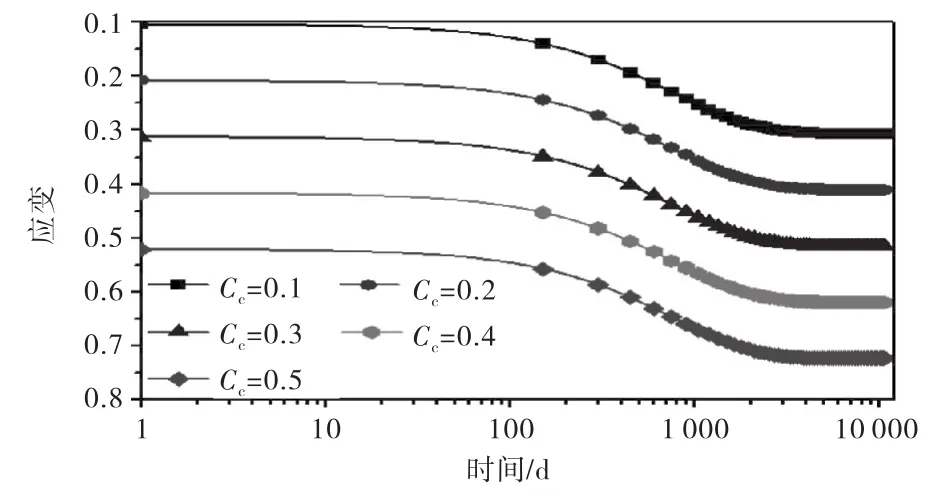
图1 压缩系数对总应变的影响

式中，H为填埋场的总高度；ΔH为沉降量；C'c为压缩系数；Δσ为竖直方向应力增量；b为机械蠕变系数；c是机械蠕变速率常数；Edg是生化降解引起的总应变变形；d是生化降解速率常数；t'是施加应力的时间；t″是垃圾开始填埋的时间.

将复合压缩模型的式(7)代入到式(6)中，即可获得降解和压缩作用下垃圾土气体渗透率非线性定量表征模型，见式(8)：

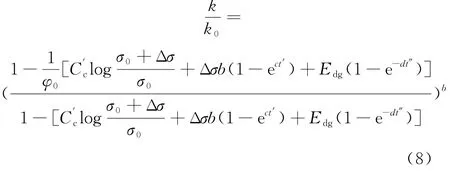
2 气体渗透率非线性定量表征模型参数灵敏性分析

2.1 降解和压缩参数对复合压缩模型的影响

复合压缩模型模拟时参数取值为Δσ=100 k Pa，m2/k N，c=1.79×10-3d-1，d=1.14×10-3d-1[18].对复合压缩模型的等4个参数对应变的影响进行了模拟，时间为30年，结果如图1～4所示.

由图1到图4可知，压缩系数主要影响瞬时沉降，随着压缩系数的增大，前期的应变增长较大；随着机械蠕变系数的增大，变形不断增大，但总的变化幅度约5%，对总应变的影响较小，参数灵敏性分析时可忽略；生物降解应变对前50 d的沉降变形影响较小，随着的增大，后期的总应变不断增大，变化幅度约17%；生物降解速率常数对前20 d的变形影响小，最终的变形相等，中间的时间阶段随生物降解速率常数增大，变形不断增大.

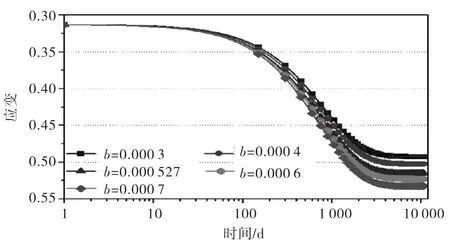
图2 机械蠕变系数对总应变的影响

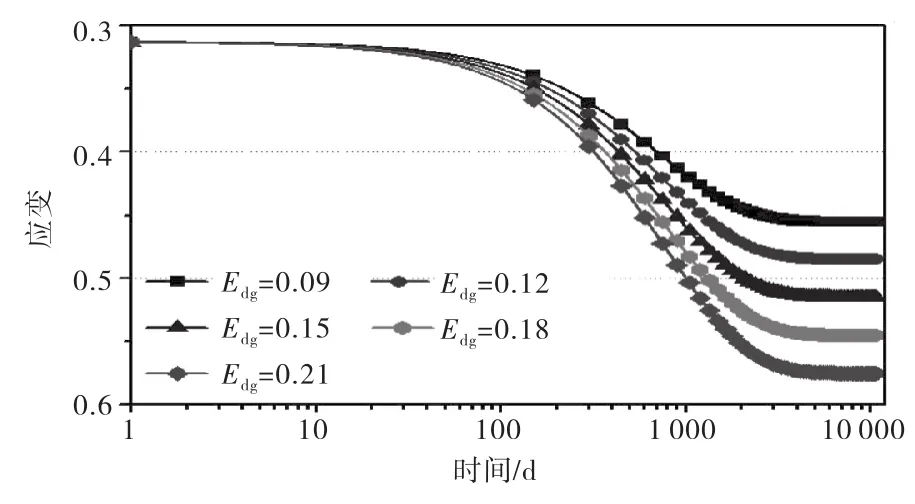
图3 生化降解应变对总应变的影响

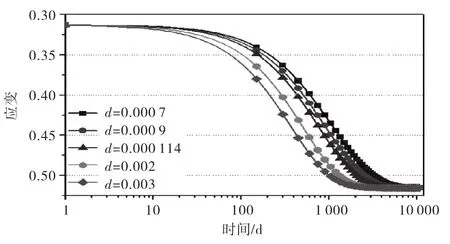
图4 生化降解速率常数对总应变的影响

2.2 降解和压缩参数对气体渗透率定量表征模型的影响

对式(5)中参数取值如下，k0=1×10-12m2，φ0=0.6，幂指数取2.5，将上面的复合压缩模型计算的应变代入到式(6)中，可得到各参数对气体渗透率的影响如图5～7所示.

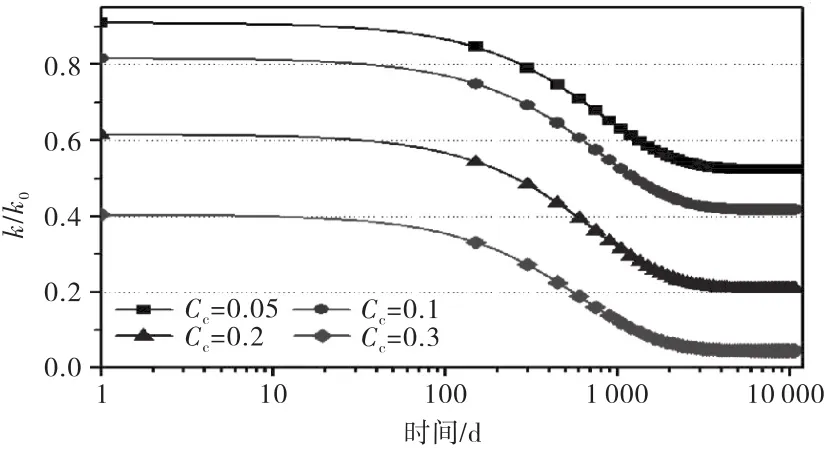
图5 压缩系数对k/k 0的影响

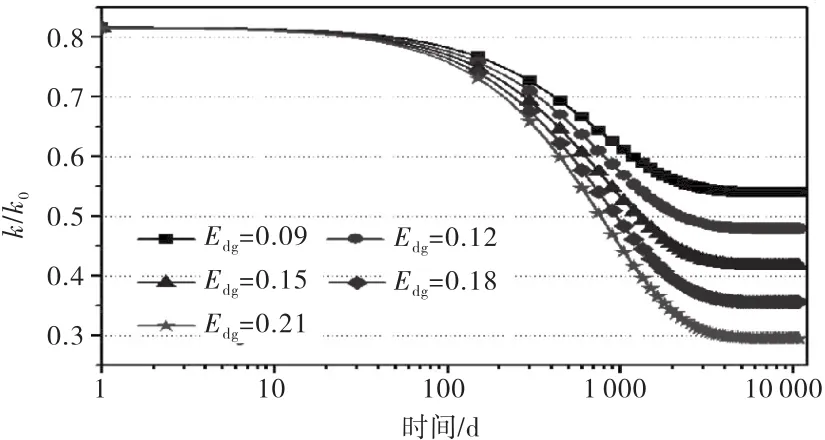
图6 生化降解应变对k/k 0的影响

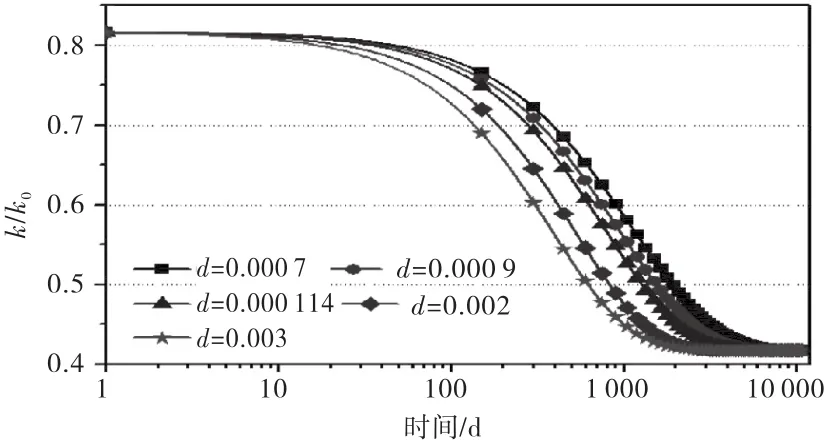
图7 生化降解速率常数对k/k 0的影响

由图5～7可知，随着压缩系数的增大，k/k0数值减小的较大，主要是因为压缩系数使变形增大，孔隙度减小，而导致k/k0数值显著降低，当压缩系数为0.3时，在1 080 d时渗透率的数值减小了2个数量级；生化降解应变对k/k0的影响主要是后期的降解沉降阶段，随着生化降解应变的增大，k/k0不断的减小.生化降解速率常数对k/k0的影响主要在中间降解阶段，且k/k0随着生化降解速率常数的增大而减小，最终k/k0的数值相等.

2.3 幂指数对气体渗透率定量表征模型的影响

取k0=1×10-12m2，φ0=0.6，幂指数从0.5到6.5变化，应变的变化范围为5%到40%，φ/φ0和k/k0的计算结果如图8～9所示.

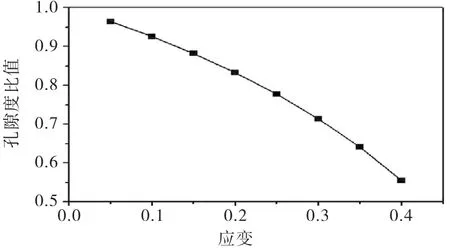
图8 应变对φ/φ0的影响

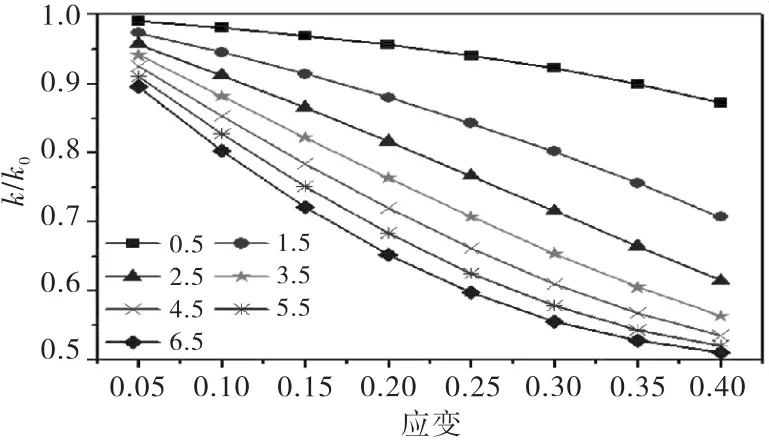
图9 幂指数对k/k 0的影响

由图8和图9可知，随着应变的增大，φ/φ0降低的幅度较大，数值可达到0.4，主要是因为应变增大使试样被压缩的更密实，孔隙空间减小.随着应变的增大，k/k0是不断减小的，且减小幅度是随着幂指数的增大而不断增大，可达到2个数量级.主要是因为应变增大使孔隙被压的更密实，φ/φ0不断减小，k/k0随着应变的增大而不断减小，φ/φ0小于1且幂指数大于1，因此随幂指数增大，k/k0减小幅度不断增大.

3 结 论

本文结合垃圾土复合压缩模型，以及表征气体渗透率和孔隙度的幂函数模型，构建了考虑降解-压缩作用下垃圾土气体渗透率非线性定量表征模型，并对模型中参数变化规律和灵敏性进行了分析，得到的主要结论如下：

1)随着压缩系数的增大，k/k0数值减小幅度的较大，可达到2个数量级.

2)生物降解应变对k/k0的影响主要是后期的降解沉降阶段，随着生物降解应变的增大，k/k0不断的减小.

3)生物降解速率常数对k/k0的影响主要在中间降解阶段，且k/k0随着生物降解速率常数的增大而减小.

4)随着应变的增大，孔隙度降低的幅度较大，数值可达到初始值的0.4；随着应变增大，气体渗透率是不断减小，且减小幅度是随着幂指数的增大而不断增大，可达2个数量级.