一种嵌入土体的锚链反悬链线形态分析软件

徐 峰，谭红莹，赵佳宁，王江宏，陈 曦

(海洋石油工程股份有限公司 天津 300451)

1 研究背景

深水系泊系统中，嵌入水底土中的锚链由于土壤提供的侧向支撑而呈现典型的反悬链线状，如图1所示。该段锚链与土体间复杂的相互作用[1]，改变了传递至系泊基础上的荷载大小与角度，并最终影响系泊基础的承载力与失效模式。

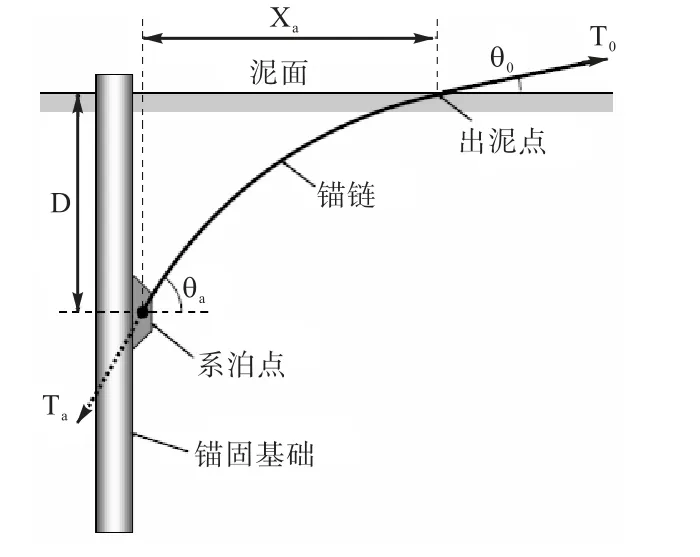
图1 锚固基础受力示意图Fig.1 Schematic diagram of force acting on anchored foundation

对于嵌入土中的锚链，国内外学者已做过大量研究。Reese[2]最早研究了锚链与土体间的相互作用，提出了假定锚链形状为多段圆弧构成的简单计算方法。Vivatrat等[3]建立了锚链微元段的微分方程，获得嵌入土体锚链的反悬链线构型。Degenkamp等[4]采用试验方法研究了锚链系泊点与出泥点荷载之间的关系。Neubecker[5]和 Randolph[6]采取逐段微分的方法推导了锚链系泊点与出泥点荷载关系的计算公式，提出了嵌入土中锚链形态的计算公式。国振等[7]建立了二维锚泊线准静力分析模型，并对考虑锚泊线切入土体段的必要性进行了分析。Wang等[8]在二维和三维空间对锚链进行了准静力分析，并对锚链在土体中滑动可能对锚泊系统造成的影响进行了研究，指出该滑动对吸力锚的承载力有影响。

然而，对于嵌入土中反悬链段的计算，国内尚未有成熟的模拟程序应用于工程项目，通常还是由国外的工程公司完成该方面的分析。本文基于 Neubecker和Randolph提出的利用微分方式求取锚链力学响应的方法[9]，建立了嵌入土中锚链段的数值计算模型，采用 MATLAB编制程序开展计算分析，并以工程项目为例，将数值分析结果与国外工程公司的计算结果进行对比，验证该数值计算模型的可靠性。

2 嵌入土中锚链的力平衡方程

嵌入土中段锚链的微元段受力如图2所示。

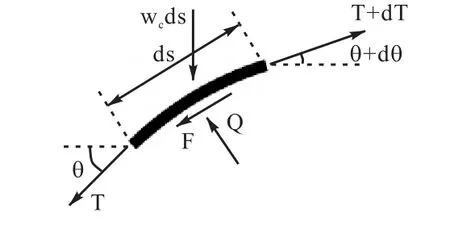
图2 土体中锚链微元体的力平衡方程Fig.1 Force equilibrium equation of anchor chain microelement in soil

图中，锚链微元段ds上荷载的减小值dT可通过下式来计算：

式中：T为锚链荷载；θ为锚链微元段方位角(θ=0°表示水平微元段)；ds为微元段长度；F为沿锚链切向的土壤阻力；wc为土中锚链单位长度的重量。

从一个锚链微元段到下一个锚链微元段的角度变化使用下式计算：

式中：Q为沿锚链法向的土壤阻力。

土壤阻力F和Q，分别采用下列公式计算：

式中：db为锚链单链环的名义直径；En、Et分别为有效宽度和周长参数；f为沿锚链切向的单位摩阻力；q为沿锚链法向的单位端阻力。在粘性土中，(α为粘结系数，su为不排水抗剪强度，Nc为承载力系数)。

3 MATLAB自编软件

本文自编软件基于2个基本假定：①锚链在基础上的系泊点为固定点，即基础承受锚链所传递的张力荷载时不会产生位移；②锚链为连续柔性，不受弯矩和扭转，只受张紧荷载[10]。

3.1 软件输入参数

系泊点在泥面下的深度值 z(m)；泥面处的锚链荷载 T(N)；锚链与泥面的夹角θ(°)；锚链的轴向刚度 EA(N)；锚链单链环的名义直径(m)；土体中锚链的单位长度重量(N/m)；锚链剖分单元长度(m)；土壤有关参数。

3.2 软件输出参数

传递到系泊点的荷载大小(N)；锚链张力的水平分量(N)；锚链张力的竖向分量(N)；锚链形态的水平坐标(m)；锚链形态的竖向坐标(m)；系泊点处荷载与水平面的夹角(°)；未张紧锚链的初始长度(m)；受载伸张后的锚链长度(m)。

4 算例验证

为保证数值计算模型结果的准确度和可靠性，选取了以下几个具有代表性的实际工程项目数据，采用MATLAB自编软件进行计算，并与国外专业岩土工程公司的计算结果进行对比验证。

4.1 算例一

某单点系泊项目，系泊点位于泥面下 14.0m 深度处，该位置以上土壤均为粘性土。泥面处的系泊荷载、与泥面的夹角、锚链以及土壤的具体参数如表1—表3所示。

表1 系泊荷载Tab.1 Mooring load

表2 锚链参数Tab.2 Anchor chain parameters

表3 土壤参数Tab.3 Soil parameters

MATLAB自编软件的分析结果如下：系泊点处张力：2847.7kN；系泊点处荷载与水平面夹角：22.08°。

4.2 算例二

系泊点位于泥面下 4.0m的位置，其上土壤均为砂土。泥面处的系泊荷载、与泥面的夹角、锚链以及土壤的具体参数如表4—表6所示。

计算中考虑了1m的整体冲刷，则系泊点位置深度变为 3m，MATLAB自编软件的分析结果如下：系泊点处张力：10746kN；系泊点处荷载与水平面夹角：29.5°。

表4 系泊荷载Tab.4 Mooring load

表5 锚链参数Tab.5 Anchor chain parameters

表6 土壤参数Tab.6 Soil parameters

4.3 算例三

系泊点位于泥面下 5.5m的位置，系泊点位置以上土壤为砂土与粘土互层。泥面处的系泊荷载等参数如表7—表9所示。

表7 系泊荷载Tab.7 Mooring load

表8 锚链参数Tab.8 Anchor chain parameters

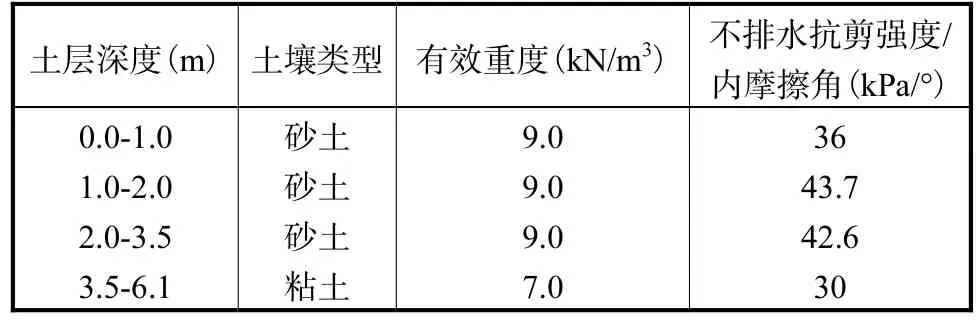
表9 土壤参数Tab.9 Soil parameters

计算中考虑了1m的整体冲刷，则系泊点位置深度变为 4.5m，MATLAB自编软件的分析结果如下：系泊点处张力 10977kN；系泊点处荷载与水平面夹角 28.3°。

4.4 结果对比

本文MATLAB自编软件计算结果与国外工程公司计算结果对比如表10所示。

由上述对比结果可以看出，算例一和算例二系泊点处荷载与水平面夹角的数值计算结果与国外工程公司计算结果误差在 4%以内，计算结果都略小于国外工程公司结果；算例二(全砂土)计算的系泊点处荷载值误差较大，约为 9%，但由于本文计算的系泊点处荷载大于国外工程公司结果，水平和竖向荷载分量都大于国外工程公司的计算结果，对设计而言是保守的；算例三的土壤情况一定要引起足够重视，表层土为砂土，其下为比较软的粘土，其承载能力受控于下层的软粘土，这种现象国外工程公司称之为“穿透现象”，数值计算和系泊点荷载与国外工程公司结果接近，但夹角偏差较大，还需进一步研究和完善。

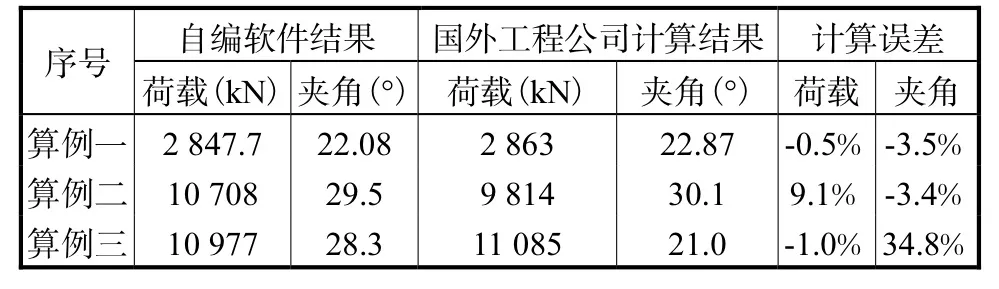
表10 计算结果对比Tab.10 Comparisons of calculation results

5 结 论

①本文建立了一种利用微分方式求取嵌入土中锚链段锚链力学响应的数值计算模型，并通过MATLAB编程实现可操作化。

②通过与国外工程公司计算结果对比，验证了MATLAB自编软件计算结果的准确度和可靠性；对于均质土，与国外工程公司计算结果误差较小，可用于指导工程设计。

③对于存在软弱下卧层的地层，由于可能会产生穿透现象，自编软件计算的系泊点处荷载与水平面夹角误差较大(约为 35%)。对于此地层情况的嵌入土体中的反悬链线分析还需进一步研究。