变化海况下推力分配多模式自适应切换研究*
朱梦飞 徐海祥 余文曌 李文娟
(武汉理工大学高性能船舶技术教育部重点实验室1) 武汉 430063)(武汉理工大学交通学院2) 武汉 430063) (江苏科技大学海洋装备研究院3) 镇江 212003)
0 引 言
多个推进器的配置在海洋平台、工程船、半潜船和新型无人艇上广泛应用,其在执行任务时面临变化海况和多种工况,因此,需制定多种推力分配模式以满足作业需求和提高推进器控制系统的稳定性.在实际推力分配过程中,由于环境力的变化,往往会导致当前海况和工况下单一推力分配算法无法解决分配问题,因此,需要建立合理的推力分配切换机制,并采用合适的推力分配算法来实现多推进器多模式间的相互切换.
Swanson[1]将海况分为平静海况和恶劣海况,以能耗大小作为切换指标,设计了固定角度和可变角度两种分配模式,减少了全回转推进器角度的频繁改变,降低了机械系统的磨损,但该方法切换指标单一且未考虑控制力的特性,无法有效地反映实际情况.Ruth[2]提出以待分配力和力矩的特性作为参考指标,并提出了迟滞切换的概念,但该方法忽略了分配误差、能耗等重要指标.杨世知等[3]给出了一种依据环境力方向确定全回转推进器方位角的方法,针对伪逆法的特性,提出了三种分配模式,但该方法局限于伪逆法,没有考虑推进器的物理限制,无法对推力角度进行优化.王芳[4]考虑能量消耗、控制误差,以及响应时间等性能指标,建立了基于固定方向角模式与可变方向角模式的分配策略,但该方法对全回转推进器最小推力限制考虑不周.许林凯[5]探讨了用于不同典型海况及工况下分配模式的切换,但多重指标的各项权值因子选择困难.周兴[6]以控制力、能耗项作为对应海况的切换指标,以当前位置与期望位置的差值作为工况的切换指标,建立了分级处理的切换机制,但是由于未考虑环境力的特性而无法反映真实的推进器状态.付海军[7]设计了三种推力分配模式并制定了模式切换标准,但其只设定了四种环境力固定角度,对固定角度模式下的环境力方向考虑欠妥.
在分析相关文献的基础上,针对变化海况下船舶的推力分配问题,考虑全回转推进器无法提供零推力等特殊情况,本文设计了可变方位角、固定方位角和推进器偏置[8-10]等三种推力分配模式,以环境力、推力误差、推进器限制等作为切换指标,建立具有迟滞切换逻辑的切换机制,采用三种推力分配算法对应三种分配模式,求解得到优化后各推进器的推力与角度,实现三种分配模式的自适应切换.通过对一艘配置有四个推进器的船舶模型进行仿真实验,验证了该切换方法的有效性与可行性.
1 推力分配模式的设计
为满足海洋平台、各类动力定位船舶在海上作业应对变化海况、不同工况的要求,需要根据船舶实际推进器配置、外界环境、工作模式等制定多种相适应的推力分配模式.本文以一艘配置有四个推进器的船舶模型为对象,考虑变化海况、不同工况、推进器的限制,以及系统稳定性等,设计了三种分配模式:可变方位角模式、固定方位角模式和推进器偏置模式.
1.1 可变方位角模式
当船舶所受环境载荷较大且方向较为稳定时可启用该模式;当船舶处于定点定位、循迹、跟踪等工作模式也能启用该模式.系统自动改变全回转推进器的推力和角度,以产生所需的力和力矩,使推力始终作用于最优方向,即能耗最小.为了减少全回转推进器的连续转动以及推进器间的水动力干扰引起的机械磨损与推力效率下降.全回转推进器禁区ψ禁区为
|ψ禁区-θi|≥δi
|ψ禁区-θi|≤360°-δi
(1)
式中:θi为相邻两个推进器连线与X轴夹角;δi为推进器的禁区角.
图1为相邻两个全回转推进器之间的禁区设置图.

图1 全回转推进器禁区设置
1.2 固定方位角模式
当环境载荷较小且方向频繁改变时可以启用固定方位角模式;当定位精度要求不高时也可启用此模式,以避免全回转推进器角度的连续变化,减少推进器的磨损与能量消耗.预设多组固定方位角,同时需避开全回转推进器禁区,系统根据环境力方向自动从中选择最佳方位角.基于以下因素预设固定方位角模式的推进器角度:
1) 当前可用的推进器数量.
2) 推进器/船体之间相互干扰,如柯安达效应.
3) 推进器/推进器之间的相互干扰,主要取决于推进器之间的距离、方位角等.
4) 推进器/其他设备之间的相互干扰.
1.3 推进器偏置模式
当船舶处于外界环境力方向频繁大角度变化,全回转推进器无法输出零推力,以及为保证电力系统的功率平衡而要求高于实际所需功耗等特殊状况时,可启用推进器偏置模式以保证船舶的操纵性、定位精度和电力系统的安全性.在进行高精度定点定位作业时也可启用此模式.该模式对全回转推进器进行分组,允许全回转推进器之间相互抵消推力,各个组可以包含两到三个推进器,其中偏置量是指运行推进器使之相互抵消时,各推进器相互抵消的推力.图2为全回转推进器组合偏置示意图.
2 推力分配优化算法
2.1 推力分配数学模型
2.1.1约束条件
在满足动力定位系统中三个自由度控制力与力矩的前提下,考虑推进器的物理限制与机械磨损,则本文的推力分配模型中的约束条件表示为
τ=B(a)T+s
(2)
Tmin≤T≤Tmax
|T-T0|≤ΔT≤|T+T0|
|α-α0|≤Δα≤|α+α0|
|ψ禁区-θi|≥δi
|ψ禁区-θi|≤360°-δi
(3)
式中:τ=[τX,τY,τN]∈R3为控制力与力矩;T=Ti为各推进器的推力;T0为推进器上一时刻推力;α=[αi]为各推进器的方位角;s为松弛变量;α0为推进器上一时刻方位角;i为推进器个数;ΔT为推力变化率;Δα为角度变化率;B(α)为推进器的配置矩阵,
(4)
其中:lxi,lyi为第i个全回转推进器位置坐标.
2.1.2目标函数
本文以船舶能耗最少、推力误差最小及推进器机械磨损最小为目标,其目标函数为
(α-α0)TΩ(α-α0)
(5)
式中:第一项表示船舶能耗;第二项为推力误差惩罚项,W为正定对角矩阵;第三项为推进器磨损惩罚项,Ω为正定对角矩阵.
2.2 二次规划有效集法
利用二次规划有效集法解决可变方位角模式下的推力分配问题,该方法将非线性的推力分配优化问题转换成一个带有线性约束的标准二次优化问题进行求解.二次规划有效集法的步骤见图3,具体计算方法参照文献[6].

图3 二次规划有效集法
2.3 直接分配法
采用直接分配法求解固定角度模式下的推力与角度.该方法将复杂的数学问题转化为直观的几何问题,通过搜索期望输出力与力矩矢量和可达集凸多面体各个面的交点得到相应的推进器推力、力矩.图4为该方法的实现步骤,详细计算方法见文献[11].
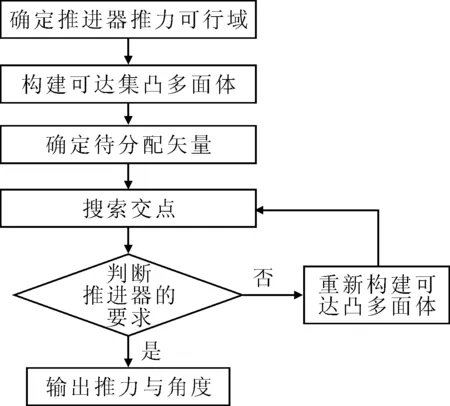
图4 直接分配法
2.4 自适应组合偏置法
采用自适应组合偏置法求解推进器偏置模式下的推力与角度.该方法采用伪逆法求解得到推进器的推力与角度,然后根据待分配力的特性选择组合的推进器进行偏置,选取角系数并确定偏置量,进而计算得到偏置后的推进器推力与角度.图5为自适应组合偏置法的流程,具体算法步骤见文献[10].
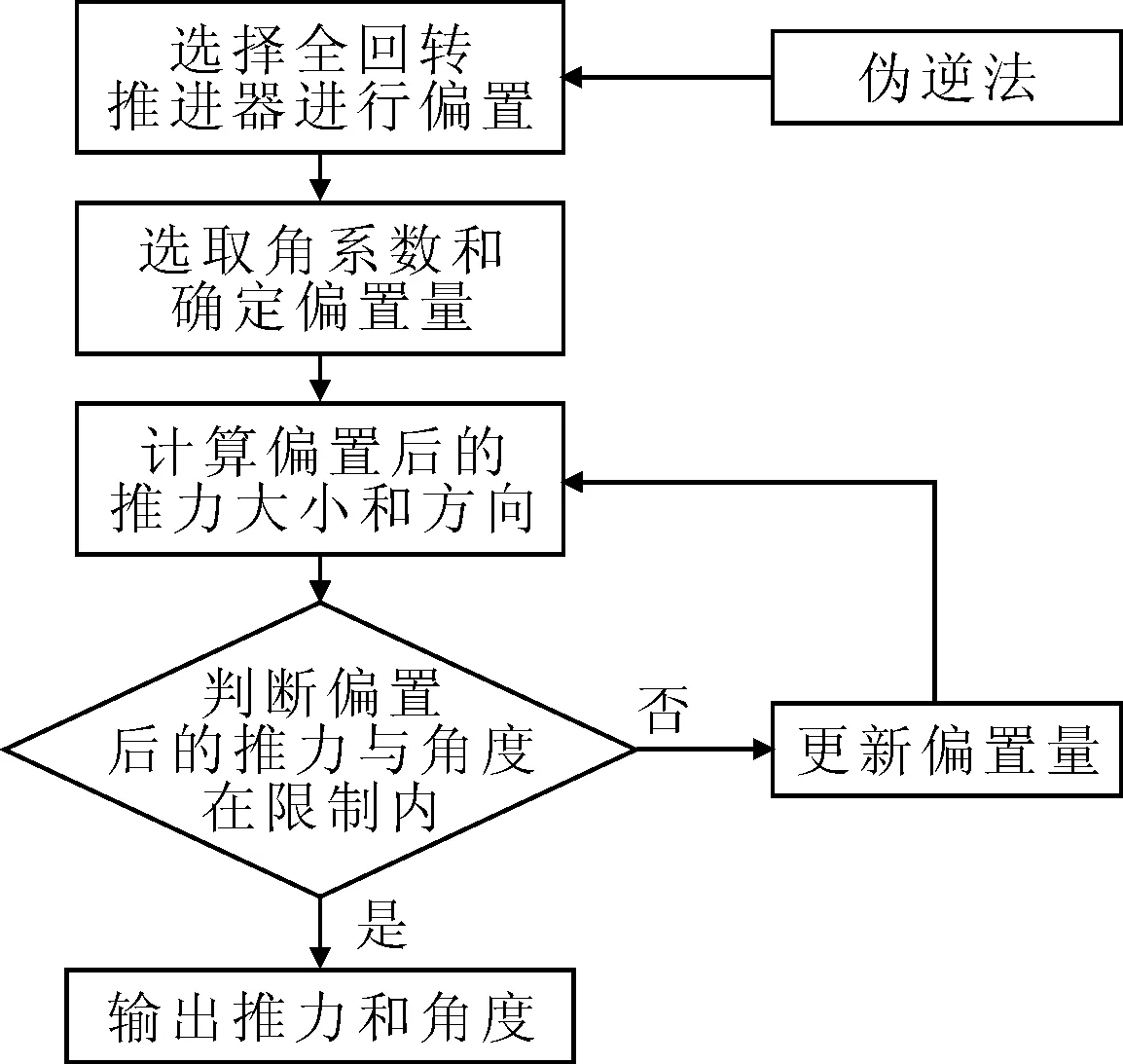
图5 自适应组合偏置法
3 切换机制的建立
3.1 切换指标
建立切换机制需要有效的切换指标,使得不同的分配模式能适应变化的海况.本文针对所设计的是三种分配模式,结合能耗、环境力、推进器限制及推力误差等因素,分析其在不同模式中的特性,分别为三种分配模式设置相应的有效切换指标.
提出如下的切换指标函数:
S=J(u,T)+B(R(ψ),b)+
P(Δα,Tmin/max,ΔT)+e(u,τ)
(6)
式中:J(u,T)为能耗监督函数(u为推力矢量),用于判断系统能耗大小;B(R(ψ),b)为环境力监督函数(R(ψ)为坐标转换矩阵,b为环境力和力矩),用于判断环境力变化;

P(Δα,Tmin/max,ΔT)为全回转推进器限制的判断函数(Tmin/max为推进器推力上下限),用于判断推进器的状态;e(u,τ)为推力误差监督函数,用于判断控制力与推力之间的误差.
由于海洋环境载荷的大小与方向直接影响推力分配模式的选择,而且船舶在执行作业任务时所受环境载荷通常较大且方向稳定,因此本文设置可变方位角模式作为系统默认模式,考虑如下推力分配模式切换情况:
1) 可变方位角模式向固定方位角模式切换 当监督器发现一段时间内环境载荷较小且全回转推进器发出的力满足限制要求,且环境载荷方向不断小角度变化,系统根据环境力监督函数B(R(ψ),b)、推力误差监督函数e(u,τ)、能耗监督函数J(u,T)选择固定方位角模式.
2) 固定方位角模式向可变方位角模式切换 当监督器发现一段时间内环境载荷变大或方向变化稳定,且全回转推进器发出的力满足限制要求,系统根据环境力监督函数B(R(ψ),b)、推力误差监督函数e(u,τ)切换至可变方位角模式.
3) 启用推进器偏置模式 当监督器发现全回转推进器发出的力接近最小推力限制,或环境力的方向频繁大角度变化,或为保证电力系统的功率平衡而要求高于实际所需功耗等特殊状况,系统根据推进器限制判断函数P(Δα,Tmin/max,ΔT)、推力误差监督函数e(u,τ)、环境力监督函数B(R(ψ),b)和能耗监督函数J(u,T)选择推进器偏置模式.
3.2 切换逻辑
滞后切换逻辑不仅适用于线性系统间的切换,同时也适用于非线性系统或非线性系统与线性系统间的切换.因此,本文设计了适合非线性推力分配模块的迟滞切换逻辑,设置合理的迟滞时间以避免频繁切换的发生.当切换指标即监督信号发生改变,迟滞切换逻辑不会立即进行切换,也不会驻留一个固定时间后进行切换,而是通过对一段时间内的切换指标函数进行判断,达到切换标准后改变当前分配模式即切换信号,从而实现推力分配模式的切换.图6为迟滞切换逻辑流程图.
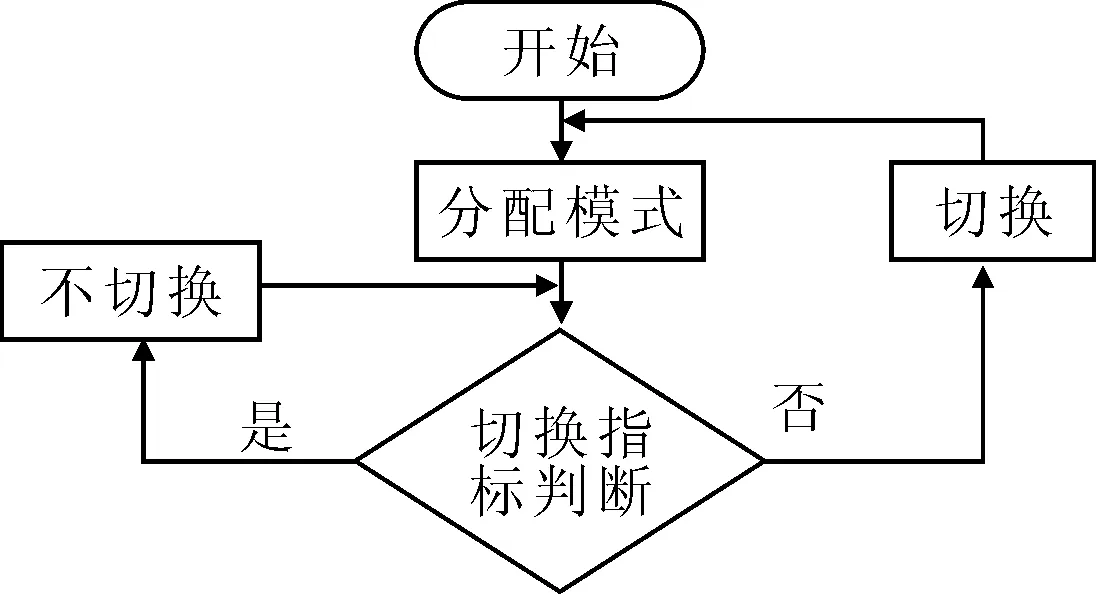
图6 迟滞切换逻辑
3.3 切换机制
单一的推力分配算法、分配策略或分配模式往往无法解决变化海况下实际的推力分配问题,从而影响系统的稳定性、安全性.本文采用三种推力分配算法对应求解三种分配模式下的推力优化问题,结合所设置的切换指标与切换逻辑,建立合理的切换机制,从而实现船舶推力分配多模式的自适应切换,完成有效的推力分配.综上所述,本文提出的推力分配多模式自适应切换方法流程见图7.

图7 推力分配多模式自适应切换流程
4 仿真实验
4.1 仿真参数
为验证本文提出的变化海况下推力分配多模式自适应切换方法的有效性,以一艘配置四个推进器的船舶模型为对象进行仿真分析.推进器的布置见图8,其中1#和2#推进器为全回转推进器,3#和4#推进器为槽道推进器;其相关技术参数见表1.
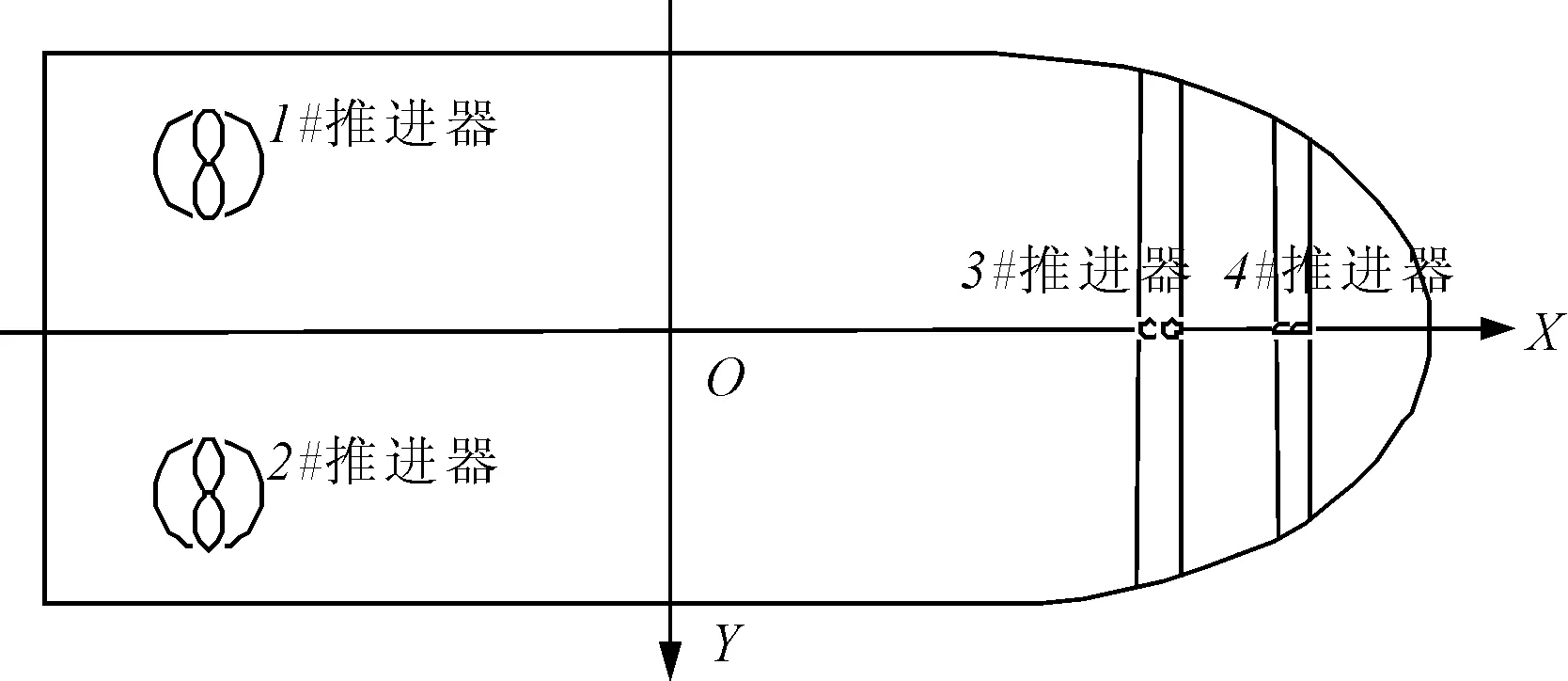
图8 推进器布置
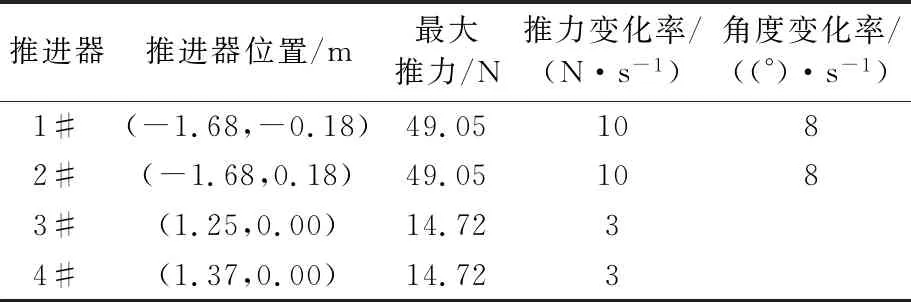
推进器推进器位置/m最大推力/N推力变化率/(N·s-1)角度变化率/((°)·s-1)1#(-1.68,-0.18)49.051082#(-1.68,0.18)49.051083#(1.25,0.00)14.7234#(1.37,0.00)14.723
注:1-可变方位角模式;2-固定方位角模式;3-推进器偏置模式.
4.2 仿真结果与分析
图9~10为推进器推力和全回转推进器角度曲线.图11 为误差曲线,图12为模式切换信号.

图9 推进器推力曲线

图10 全回转推进器角度曲线

图11 误差曲线
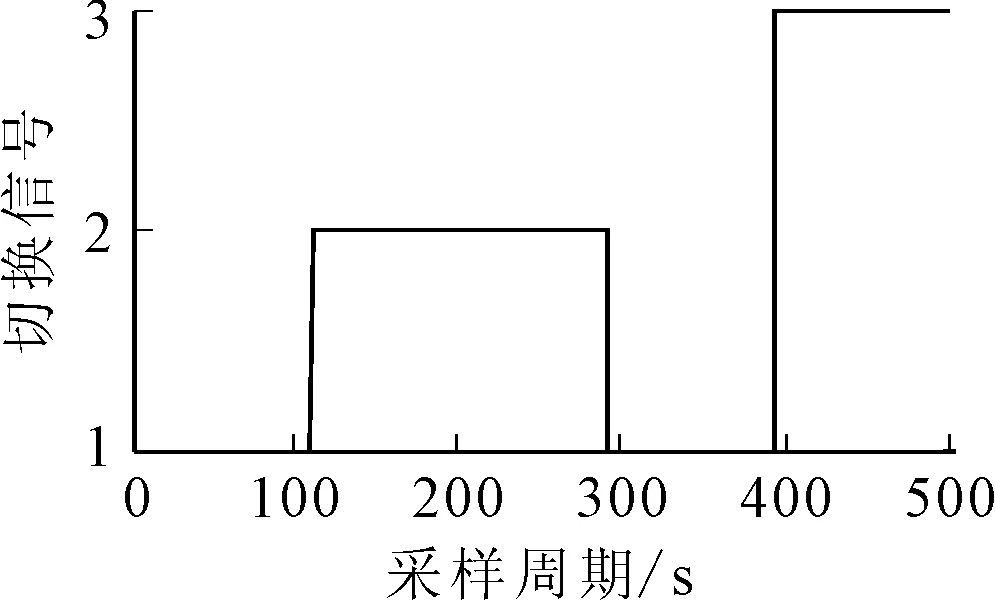
图12 模式切换信号
阶段Ⅰ(0~110 s)环境力较大,系统选择默认的可变方位角模式;由图9~10可知,系统在阶段Ⅰ不断调整推进器的推力与角度,以使推力作用于最优方向而减小能耗,虽然全回转推进器的方位角在0°~360°内变化,但实际方位角0°即为360°,推进器角度变化满足限制要求;由图11可知,初始阶段存在较小的推力误差,但满足系统稳定性要求.
阶段Ⅱ(100~290 s)外界环境力变小,由图11~12可知,系统主要根据环境载荷、推力误差变化与物理限制而切换至固定方位角模式;由图9~10可知,全回转推进器此时角度固定为0°,270°,能够很好的减小能耗与机械磨损;由图11可知,系统处于固定方位角模式的推力误差满足要求.
阶段Ⅲ(290~390 s)环境载荷变大,系统主要根据环境力、推力误差变化等切换至可变方位角模式,以应对变化的海洋环境力.
阶段Ⅳ(390~500 s)环境力变得非常小,由于全回转推进器无法发出零推力,为保证船舶的定位精度,系统主要根据推进器限制、推力误差变化、能耗与环境载荷启用推进器偏置模式;由图9~10可知,偏置模式下,由于偏置量的存在,使得推进器推力变化较剧烈,但满足全回转推进器的物理限制,且其发出的推力相互抵消而使得系统能耗增大以提高船舶定位精度与响应能力.
由上述可知,仿真实验中各推进器的推力和角度满足物理限制,能够完成变化海况下船舶的推力分配任务,表明本文设计的推力分配模式与切换机制可以有效地实现多模式的自适应切换.
5 结 束 语
本文针对船舶处于变化海况的推力分配问题,根据海况与工况设计了三种分配模式,考虑环境力、能耗、推进器限制和推力误差等因素设置了合适的切换指标,以此建立基于多切换指标与迟滞切换逻辑的切换机制,进而应用适合不同海况的推力分配优化算法实现多模式的自适应切换.仿真结果表明:该方法能够有效地实现多种模式的自适应切换,完成变化海况下动力定位船舶推力分配任务.

