寒区城市轨道交通合理分担率研究*
冯天军 程国柱 马俊风
(吉林建筑大学交通科学与工程学院1) 长春 130118) (东北林业大学交通学院2) 哈尔滨 150040)(哈尔滨工业大学交通科学与工程学院3) 哈尔滨 150090)
0 引 言
城市轨道交通具有准时、安全、恶劣天气影响小等诸多优点,是解决寒冷地区城市交通问题的重要手段.
目前,我国尚处于城市轨道交通建设的探索阶段,轨道交通建设没有形成完整的标准体系,不能满足交通快速发展的要求,导致规划阶段缺乏相关的研究依据,在制定轨道交通分担率宏观规划时存在一定的盲目性,制约城市的发展.另外,我国已经通过国家轨道建设批复的城市有44个,位于寒区的城市达到16个,所占比重较高,而寒区城市出行环境较差,其轨道交通的分担率理应高于其他城市,因此,有必要对其开展相关研究.
轨道交通分担率的预测是交通方式划分中的一方面,主要有集计方法和非集计方法两大类方法[1].Daniel[2]从非集计模型的角度,提出了基于随机效用模型的Logit模型.Ben等[3]将Logit模型应用到各交通方式分担率计算中去,被认为是统计学与交通领域结合的一大创举.Koppelma等[4-6]分别从不同的角度,利用Logit模型计算城市交通结构.裴玉龙等[7]采用模糊推理方法,建立了公共交通分担率预测模型,选取了公交服务水平、社会发展状况、交通时间三个指标层、十个具体指标,分析了影响因素与分担率水平之间的关系.胡晓伟[8]分析了公交、轨道交通和出租车三种公共交通方式之间的Nash均衡,利用博弈模型来描述城市客运交通运营者之间的经济决策行为.
综上,目前轨道交通分担率的预测方法主要采用Logit模型,通过分析出行者效益确定轨道交通分担率.实际上,我国城市交通系统并不仅仅由出行者主导,还受到政府管理者的宏观调控.一方面,出行者总是以自己的效益最优来选择出行方式,另一方面,管理者会依据城市发展状况进行交通资源的优化配置,而管理者的宏观调控会影响出行者的选择行为.从管理者的社会效益最优,出行者自身效益最优两个方面来确定合理的城市交通结构,采用Stackelberg博弈模型建立管理者和出行者之间的双层规划模型,为寒区城市轨道交通规划提供理论依据.
1 轨道交通分担率的分析与建模
1.1 上层规划模型
出行者交通方式选择是一个概率问题,根据弱大数理论,城市中各交通方式的分担率就是出行者交通方式选择的概率.
出行者选择交通方式时,总是力图选择效益最大的交通方式,而影响出行效益的因素较多,主要从经济、效率、安全、舒适四个角度考量出行者成本.出行者效益最优的上层规划模型为
式中:RC为出行者的出行成本,元/d;ECi为出行者的经济成本,元/次;TCi为出行者的时间成本,元/次;CCi为出行者的事故成本,元/次;FCi为出行者的舒适性效益,元/次;Pi为各交通方式的分担率,i为各交通方式,从1~4分别为私家车、出租车、公交车、轨道交通;O为四种出行方式出行总量,次/d.
1.2 下层规划模型
在衡量管理者的成本时,参考国民经济效益的计算方法,主要选取国民经济效益中可量化的部分,包括能源消耗成本、空气污染成本及客流票价收益三方面的指标.在运输能力满足交通需求的条件下,管理者成本最低的下层规划模型为
(2)
式中:RB为管理者社会成本,元/d;ENi为管理者的能源成本,元/次;WRi为管理者的污染成本,元/次;ETi为管理者的经济效益,元/次;Fi为各交通方式的出行频次,次/d;Hi为各交通方式平均载客量,人/次.
2 出行者和管理者指标的量化
2.1 出行者指标
2.1.1经济成本
对于出行者而言,选择不同交通方式时经济性占有很大的影响因素.采用公共交通方式出行的出行者,其成本可视为平均出行距离对应的票价,对于小汽车交通方式,其成本包含燃油费、折旧费、停车费、检修保养费等,需依据城市具体情况进行折算.
2.1.2安全成本
安全性是寒冷地区出行者出行时考虑的重要因素,由于路面行车条件差,机动车交通方式发生事故的概率较大,轨道交通不受气候的影响,是一种安全的交通方式.出行者的安全成本可以用交通事故的概率和事故财产损失进行计算,为
CCi=M×CPi
(3)
式中:M为平均每起事故的财产损失,元;CPi为各交通方式发生事故的概率,用城市各交通方式发生事故的数量与出行量的比值估算.
2.1.3时间成本
出行者考虑出行时间时要包含行驶时间和候车时间两部分,然后将出行者的时间货币化.行驶时间根据城市居民出行调查中居民的平均出行距离和不同交通方式的行驶速度确定.公共交通方式的候车时间和其运营频次有关,运营频次高,则候车时间短,运营频次低,则候车时间长,可用反比关系进行简化估计.出行者时间成本的计算公式为
(4)
式中:L为居民的平均出行距离,km;Vi为寒区城市各交通方式平均行驶车速,km/h;为出行者单位时间的价值,元/h;TH为各公共交通方式的运营时间,出租车为全天运营,公交车和轨道交通运营时间一般为15 h;αi为候车时间系数.为了使行驶时间和候车时间比例协调,根据2015年哈尔滨市公共交通运营现状调查,设置出租车候车时间系数为10,公交车候车时间系数为15,轨道交通候车时间系数为5.
2.1.4舒适性效益
舒适性是寒冷地区出行者考虑的重要因素,由于气候寒冷,路面行车条件差,小汽车车内温度上升较慢,所以寒区出行者与其他地区出行者对不同交通方式的舒适性感知有较大差别.
舒适性是基于出行者感受的心理和生理的综合性指标,文中采用结构方程推算方法,利用调查数据,建立舒适性评价函数,考虑不同舒适度情况下乘客的时间价值,从而得到不同出行方式的舒适性成本.出行者舒适性效益计算公式为[9]
FCi=LEVi×MF
(5)
式中:LEVi为各交通方式舒适性等级;MF为不同等级对应的成本,参考文献[11]关于舒适性时间价值的研究,设定出行者舒适度为5时的效益为8.6元.
综合乘车舒适性的研究成果[10],构建了如图1所示的结构方程模型,选择感知质量、设施水平和出行便利三个潜在外生变量,以及出行舒适一个潜在内生变量,针对各潜变量设置了12个观察变量.

图1 结构模型图
针对结构方程模型设计调查问卷,并在寒冷地区开展出行者乘车舒适性问卷调查,期间共发放问卷500份,剔除数据信息不完整、不清晰的问卷,获取有效样本432份,为保证样本可靠性,对调查数据进行了信度和效度检验,总体α系数达到了0.88,信度较高,可进行下步拟合.在数据通过检验后,利用AMOS软件对数据进行拟合,表1为拟合指标表,表2为变量相互关系表,←为单向影响.
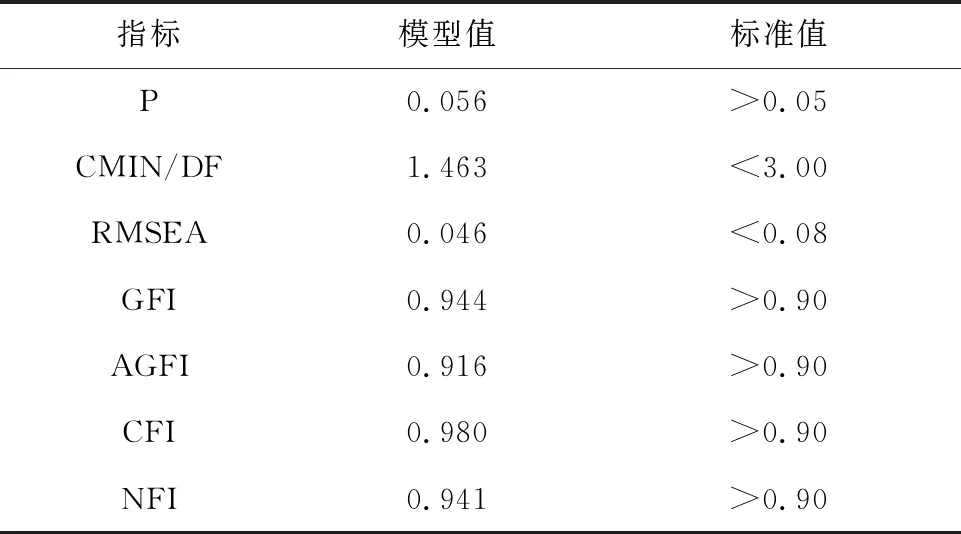
表1 模型的拟合指数
参考满意度指标的计算公式,计算出各交通方式的舒适度值,见表3.由表3可知,在寒冷地区,私家车因处于环境独立、卫生条件好、出行便捷,舒适度最高;轨道交通由于运行速度快、发车频率高、无延误等,也获得较高舒适度;出租车和公交车舒适度都比较低,主要是因为运行频率低、拥堵延误以及车内环境差等.
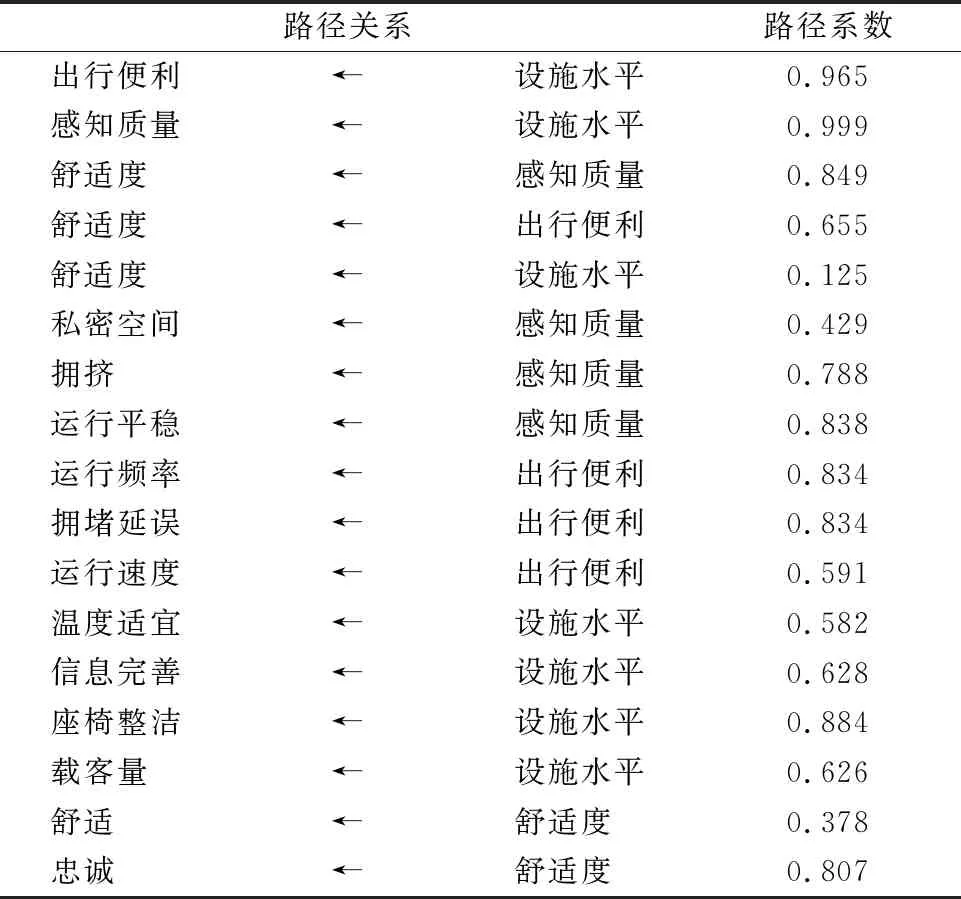
表2 变量路径系数表

表3 各机动车交通方式舒适度及效益
2.2 管理者指标
2.2.1能源成本
能源指交通工具所消耗的资源,机动车主要使用汽油,而轨道交通使用的是电能来运营.各交通方式的能源消耗成本计算公式为
ENi=Fi×Hi×L×ei×k
(6)
式中:ei为各交通方式单位能量消耗,L/(人·km);k为能源的价格,元/L.
文献[14]对不同的交通方式的能源消耗进行过研究,得到不同交通工具的单位能耗见表4.由表4可知,轨道交通的能量消耗约为小汽车的十分之一.

表4 各交通工具能量消耗标准
2.2.2环境成本
在车辆行进过程中,机动车产生大量的有害尾气,其尾气治理已成为经济活动中一项重要的工程.空气污染成本计算的关键是获取各交通方式污染物的排放量和污染物的单位治理成本.本研究参考文献[10]的机动车污染物排放模型为
(7)
式中:EFij为第i种交通方式的第j种污染物的排放因子,g/km;CFj为第j种污染物的治理成本.
机动车交通运行产生的尾气中最主要的污染物包括NOx,HC,CO和PM,每种污染物的治理成本不同,参考已有的机动车尾气成本研究成果,治理1 kg的NOx的成本为16.68元,治理1 kg的HC成本为3.79元,治理1 kg的CO成本为13.47元,治理1 kg的PM成本为1 111.00元.各种交通方式排放因子采用北京环境保护科学研究院的研究成果,见表5.

表5 机动车尾气排放因子 g/km
2.2.3运营收益
公共交通方式运营过程中,收益主要来源于乘客的乘车费用,所需要的成本主要包括车辆购置、维修保养及运营管理等费用,另外公共交通所获得的收益绝大部分都投入到了系统建设中,大部分城市甚至需要国家补贴,所以,将票价收益的一部分作为公共交通管理者的收益,计算公式为
ETi=0.05O×Pi×fi
(8)
式中:fi为票价,元/人.
3 分担率计算
3.1 理论值确定
已有研究表明,双层规划的求解是一种NP-hard问题,国内外学者就双层规划问题提出了很多求解方法,包括遗传算法、罚函数法、模糊函数法、分枝定界法等,多数方法都只能求解出局部最优解.文中采用一种近似算法,首先求出上层主导目标函数的最优解,然后将上层目标函数及其最优解作为下层函数的一个约束条件,计算下层函数的相对最优解,表达式为
(9)
3.2 案例分析
3.2.1参数设置
选取寒冷地区典型城市哈尔滨市作为研究对象,通过调查和查询相关统计资料可知,市区人口474万,出行强度为2.03人次/d,平均出行距离为6 562 m,四种机动交通方式占总出行的50%,假设未来一定时期其他交通方式分担率不变,则四种交通方式分担率扔保持在50%左右.根据哈尔滨市民收入水平,设定出行者时间价值为50元/h.全年共发生事故3 273起,平均每起事故的财产损失为1.44万元.根据调查结果,各参数设置见表6.

表6 模型参数标定
将各参数带入轨道交通分担率模型中.另外,根据哈尔滨城市的具体情况,对各个变量进行一定的约束,上层出行者成本最小的优化目标函数表达式为
13.39P4+6 000P2/F2+
5 625P3/F3+1 875P4/F4
(10)
下层管理者成本最小的优化目标函数为
0.02F4+2 400 503P2+150 031P3+300 062P4
(11)
3.2.2计算结果
用Matlab、Lingo等优化工具,求解上层优化函数的最优解,结果为30.04元,表示出行者出行的最小成本为30.04元.将出行者成本最小作为下层目标函数的一个约束条件,则管理者成本最小的目标函数为
2 400 503P2+150 031P3+300 062P4
(12)
利用优化工具求解,得到下层目标函数的最优解,见表7.现状四种方式占所有整个系统的52.10%,规划中未来将会达到65.00%.目前轨道交通的分担率比较低,小汽车交通分担率偏高;规划中出租车比例偏高,公交车和轨道交通分担率偏低.建议交通管理部门对私家车与出租车采取一定的限制措施,加大对城市轨道交通的投资与建设力度,提高城市轨道交通的服务水平.
4 结 束 语
应用双层规划模型描述了私家车、出租车、公交车和轨道交通在方式选择方面的竞争问题,模型考虑了城市管理者和交通出行者的双重效益.交通管理者和出行者效益指标的量化是模型建立的重要内容,二者效益的影响因素较多,选取了出行者的经济、安全、时间、舒适性和管理者的能源、环境、收益等指标.以哈尔滨市为例,演示了模型的应用方法,计算出了轨道交通合理分担率,在此基础上给出了建议值.该文所建模型也同样适用于其它城市,为城市轨道交通规划提供了参考和借鉴.

