带扰动对偶模型中Erlang(2)分红决策时间下的最优分红*

傅立群, 王传玉， 王 照

(安徽工程大学 数理学院, 安徽 芜湖 241000)

0 引 言

破产理论的研究起源于20世纪60年代，针对企业风险的稳定性，Lundberd和Cramér最早分别于1909年和1955年提出了几个标准，逐渐发展成为研究企业盈余的经典的Cramér-Lundberd模型。随后1957年DeFinetti[1]在纽约第15届精算师代表大会上提出分红策略，首次将盈余通过分红释放,这在一段时间内成为破产理论研究的热点。

但实际中一些企业或公司的盈余过程用上述模型来进行解释不是很合理，例如像石油、制药、研究机构等企业需要先投入一笔资金，然后等到项目完成才会有回报，也就是盈余。基于这样的实际情况，Mazza和Rulliére[2]于2004年首次提出了与Cramér-Lundberd模型相对的对偶风险模型.由于红利往往是每年或每两年地定期支付，这使得要在固定决策时间对红利进行分配，于是Asmussen等[3]于2002年提出了“Erlangisation”的方法来研究有限时间的破产问题。而这一方法又被Albrecher等[4]于2011年用来研究经典的Cramér-Lundberd模型中的分红问题. 此外Zhu和Yang[5]也在2008年提出一个对偶Markov-modulated风险模型，模型通过一个潜在的Markov环境引入盈余大小及其到达时间之间的依赖关系. Cheung[6]在2011年研究了模型中Markov过程向下跳的情况。然而，具有易处理分析性质的股利预期现值的显示解仅仅存在于具有Erlang(1)交互决策时间的周期性问题。例如，Wei等[7]在2012年研究了切换布朗风险模型的状态下周期性屏障策略的最优性。 Avanzi等[8]2014年研究了具有扩散的对偶风险模型中的一个相似问题。

但是，在确定最优周期股利策略时，通常有两个主要步骤.首先，通常会提出一个候选方案(例如，障碍或阈值类型)，并获得相关的破产前的预期股利现值。 下一步是得到所提出的解的充分的分析性质(例如，函数的有界性)，并检查它是否满足所谓的验证引理的条件。 此时，不一定能得到最优策略的显示解。 例如Avanzi等[9]2013研究了一个带布朗运动的对偶风险模型，即一旦盈余达到零，就会发生破产，通过求解积分微分方程组，发现了Erlang(n)决策时间下周期障碍策略预期股利现值的隐式解。 周金乐等[10]2015年研究了在阈值分红策略下带扰动的广义Erlang(n)对偶风险模型，并得出了模型直到破产前的总红利贴现值的期望的表达式。 最近，Avanzi等[11]又在2018年研究了Erlang(2)决策时间下的最优分红，通过数值模拟的方法详细分析了当分红决策时间为Erlang(2)分布时，周期障碍策略的最优性。

在文献[10]的基础上，考虑带扰动的利润过程服从复合泊松过程时,且分红决策时间服从Erlang(2)分布下对偶模型中的最优分红。 利用数值模拟的方法，描述了最优分红策略与其他因素之间的相关变化。

1 构建模型

考虑对偶风险模型，它的分红过程可以表示为

U(t)=u-ct+σB(t)+S(t)-D(t),t≥0

(1)

定义1 盈余过程U(t)的破产时刻定义为τ=inf{t≥0:U(t)≤0}。

性质1 最终破产概率

ψb(x,i)=Px,i[τ<∞]=1,

i=1,2,…,n。

性质1的证明过程可以参见文献[10]。

定义2 分红决策时间为Erlang(n)分布时的最优策略下的分红期望现值为

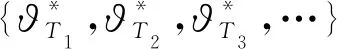
注：在一般的文献中将收益过程S(t)设为复合泊松过程，在这里为了方便计算，将其设为线性盈余，即S(t)=λt。λ为收益比率。

2 模型的应用及求解

结合文献[9]和文献[10]，对式(1)考虑一个极小的时间Δt→0，然后运用泰勒展开式可得

(2)

首次清算策略(即分红分布服从Erlang(i)分布，i=1,i=2时b*=0的情况)的微分方程组。

(3)

(4)

为解上述微分方程组，假设方程满足以下两个初始条件

初始条件1F(0,1)=F(0,2)=0；

初始条件2 当u→∞时，函数线性有界。

首先得到特征方程

其中pγ>0和sγ<0分别为方程的两个根。

运用初始条件，得到

将式(3)代入式(2)得

所以

将式(3)再次代入式(2)得

所以

那么，当b*>0，一般情况下的最优策略应满足以下微分方程组

(γ+r)FL(u,2;b*)+γFL(u,1;b*)=0

(5)

(γ+r)FL(u,1;b*)+γFL(u,2;b*)=0

(6)

(γ+r)FU(u,2;b*)+γFU(u,1;b*)=0

(7)

(γ+r)FU(u,2;b*)+γ(u-b*+FL(b*,2;b*))=0

(8)

FL(u,1;b*)和FL(u,2;b*)表示u∈[0,b*)时的情况；FU(u,1;b*)和FU(u,2;b*)表示u∈(b*,∞]时的情况。

运用初始条件

FL(u,1;b*)=FL(u,2;b*)=0

及条件

(即最优策略时所要满足的条件)由式(5)、式(6)、式(7)、式(8)解得

FL(u,2;b*)=A·g0(u)+B·g2γ(u)

(9)

FL(u,1;b*)=A·g0(u)-B·g2γ(u)

(10)

其中

g0(u)=ep0u-es0u
g2γ(u)=ep2γu-es2γu。

u-b*+FL(b*,1;b*)]+(C+D(u-b*))esγ(u-b*)

(11)

(12)

其中

+

p0>0,s0<0,p2γ>0,s2γ<0为特征方程

的4个不同的根。

(13)

(14)

将式(17)、式(18)代入式(13)、式(14)、式(15)、式(16)中，再将得到的系数A,B,C,D代入前面的式(9)、式(10)、式(11)、式(12)中，最终可以得到一个关于最优策略b*的隐式函数

(15)

3 数值模拟

为了直观地反映最优策略b*与其他变量之间的关系，通常需要写出b*与其他变量的显示表达式，但通过观察式(15)，显然无法很容易得到b*与其他变量之间的关系。因此，采用数值模拟的方法来说明最优策略b*与其他经济因素的关系。

采用Mathematica11模拟式(15)中的b*与费用率c，波动率σ，利率r，分红频率γ的关系，得到以下5个图(图1至图5)。

图1 c∈(0,3),λ=3,σ=1,r=0.1,γ=0.1Fig.1 c∈(0,3),λ=3,σ=1,r=0.1,γ=0.1

图2 c=1,λ∈(0,10),σ=1,r=0.1,γ=0.1Fig.2 c=1,λ∈(0,10),σ=1,r=0.1,γ=0.1

图3 c=1,λ=3,σ∈(0,6),r=0.1,γ=0.1Fig.3 c=1,λ=3,σ∈(0,6),r=0.1,γ=0.1

图4 c=1,λ=3,σ=1,r∈(0,0.4),γ=0.1Fig.4 c=1,λ=3,σ=1,r∈(0,0.4),γ=0.1

图5 c=1,λ=3,σ=1,r=0.1,γ∈(0,0.5)Fig.5 c=1,λ=3,σ=1,r=0.1,γ∈(0,0.5)

从图1可以观察到，由于有盈余的预期增长，费用率c很小的时候，最优策略起始于一个大于零的值。随着这种漂移的增加，但其规模仍保持在略高于起始水平，维持低派息、确保盈余不会进入破产状态的最佳障碍就会增大。但随着费用率的进一步增长，最优策略逐渐减小，由于在画图之前将收益比率确定为λ=3，故当费用率继续增长到一定程度时会发生破产。

从图2发现当λ∈(0,1.3)时，最优策略为零，此时说明了由于费用率是确定的，当收益比率过低，企业的费用大于收益时，会发生破产，故这是破产时的情形。当随着收益比率继续增加时最优策略呈急剧增加势态，这是由于收益比率和费用率以及波动率相接近，故收益比率的小幅增加会造成最优策略的大幅抖动。而随着收益比率进一步增加时，当收益比率逐渐超过费用率时，最优策略逐渐变小，且趋于稳定，且不会造成破产。

图3的波动率反映了当波动性非常低时，最佳障碍非常小，因为盈余过程破产的风险不大。随着波动性的增大，维持公司安全的最优屏障增大。当波动性进一步增加时，最优障碍开始减少，此时企业已经不值得投资。

图4中的r代表了投资者的时间偏好，r增加代表投资者变得不耐烦,更多的红利分配在每一个决策时间(减少b*)来弥补金融不耐烦。

图5中的γ增大，最优策略逐渐变大，但趋于稳定，允许更频繁的红利支付。

4 总 结

研究了带扰动的对偶模型下，当收益过程为线性收入，分红Erlang(2)分布时的最优分红策略。首先通过构建模型，在经典的对偶模型中加入σ随机收入波动项。且为了后面的计算方便，令收益过程服从线性收入，运用文献[9,10]的结论，通过类似的推导得出最优策略相关的微分方程组，得出一个关于最优策略的隐式表达式。最后运用Mathematica 11通过数值模拟的方法画出最优策略与所研究模型中其他经济因素的变化关系，且分别作出相应的经济学解释。

考虑的仅仅是收益服从线性收入的特殊情形，而在一般情况下收益服从复合泊松过程的情形尚可进一步研究。